2.3: Dividing Fractions
- Page ID
- 137905
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Suppose that you have four pizzas and each of the pizzas has been sliced into eight equal slices. Therefore, each slice of pizza represents 1/8 of a whole pizza.
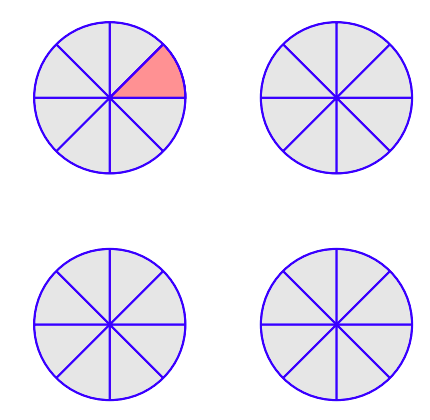
Now for the question: How many one-eighths are there in four? This is a division statement. To find how many one-eighths there are in 4, divide 4 by 1/8. That is,
Number of one-eighths in four = 4 ÷ \(\frac{1}{8}\).
On the other hand, to find the number of one-eights in four, Figure \(\PageIndex{1}\) clearly demonstrates that this is equivalent to asking how many slices of pizza are there in four pizzas. Since there are 8 slices per pizza and four pizzas,
Number of pizza slices = 4 · 8.
The conclusion is the fact that 4 ÷ (1/8) is equivalent to 4 · 8. That is,
\[\begin{align*} 4 ÷ 1/8 &= 4 \cdot 8 \\[4pt] &= 32. \end{align*}\]
Therefore, we conclude that there are 32 one-eighths in 4.
Reciprocals
The number 1 is still the multiplicative identity for fractions.
Multiplicative Identity Property
Let a/b be any fraction. Then,
\[ \frac{a}{b} \cdot 1 = \frac{a}{b} \text{ and } 1 \cdot \frac{a}{b} = \frac{a}{b}.\nonumber \]
The number 1 is called the multiplicative identity because the identical number is returned when you multiply by 1.
Next, if we invert 3/4, that is, if we turn 3/4 upside down, we get 4/3. Note what happens when we multiply 3/4 by 4/3.
The number 4/3 is called the multiplicative inverse or reciprocal of 3/4. The product of reciprocals is always 1.
Multiplicative Inverse Property
Let a/b be any fraction. The number b/a is called the multiplicative inverse or reciprocal of a/b. The product of reciprocals is 1.
\[ \frac{a}{b} \cdot \frac{b}{a} = 1\nonumber \]
Note: To find the multiplicative inverse (reciprocal) of a number, simply invert the number (turn it upside down).
For example, the number 1/8 is the multiplicative inverse (reciprocal) of 8 because
\[ 8 \cdot \frac{1}{8} = 1.\nonumber \]
Note that 8 can be thought of as 8/1. Invert this number (turn it upside down) to find its multiplicative inverse (reciprocal) 1/8.
Example \(\PageIndex{1}\)
Find the multiplicative inverses (reciprocals) of: (a) 2/3, (b) −3/5, and (c) −12.
Solution
a) Because
\[ \frac{2}{3} \cdot \frac{3}{2} = 1,\nonumber \]
the multiplicative inverse (reciprocal) of 2/3 is 3/2.
b) Because
\[ - \frac{3}{5} \cdot \left( - \frac{5}{3} \right) = 1,\nonumber \]
the multiplicative inverse (reciprocal) of −3/5 is −5/3. Again, note that we simply inverted the number −3/5 to get its reciprocal −5/3.
c) Because
\[ -12 \cdot \left( - \frac{1}{12} \right) = 1, \nonumber \]
the multiplicative inverse (reciprocal) of −12 is −1/12. Again, note that we simply inverted the number −12 (understood to equal −12/1) to get its reciprocal −1/12.
Exercise \(\PageIndex{1}\)
Find the reciprocals of: (a) −3/7 and (b) 15
- Answer
-
(a) −7/3, (b) 1/15
Division
Recall that we computed the number of one-eighths in four by doing this calculation:
\[ \begin{align*} 4 ÷ \frac{1}{8} &= 4 · 8 \\[4pt] &= 32.\end{align*}\]
Note how we inverted the divisor (second number), then changed the division to multiplication. This motivates the following definition of division.
Division Definition
If a/b and c/d are any fractions, then
\[ \frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c}.\nonumber \]
That is, we invert the divisor (second number) and change the division to multiplication. Note: We like to use the phrase “invert and multiply” as a memory aid for this definition.
Example \(\PageIndex{2}\)
Divide 1/2 by 3/5.
Solution
To divide 1/2 by 3/5, invert the divisor (second number), then multiply.
\[ \begin{align*} \frac{1}{2} \div \frac{3}{5} &= \frac{1}{2} \cdot \frac{5}{3} ~ && \textcolor{red}{ \text{ Invert the divisor (second number).}} \\[4pt] &= \frac{5}{6} ~&& \textcolor{red}{ \text{ Multiply.}} \end{align*}\]
Exercise \(\PageIndex{2}\)
Divide:
\[ \frac{2}{3} \div \frac{10}{3}\nonumber \]
- Answer
-
1/5
Example \(\PageIndex{3}\)
Simplify the following expressions: (a) 3 ÷ \(\frac{2}{3}\) and (b) \(\frac{4}{5}\) ÷ 5.
Solution
In each case, invert the divisor (second number), then multiply.
a) Note that 3 is understood to be 3/1.
\[ \begin{align*} 3 \div \frac{2}{3} &= \frac{3}{1} \cdot \frac{3}{2} ~ && \textcolor{red}{ \text{ Invert the divisor (second number).}} \\[4pt] &= \frac{9}{2} ~ && \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \end{align*} \]
b) Note that 5 is understood to be 5/1.
\[ \begin{align*} \frac{4}{5} \div 5 &= \frac{4}{5} \cdot \frac{1}{5} ~ && \textcolor{red}{ \text{ Invert the divisor (second number).}} \\[4pt] &= \frac{4}{25} ~ && \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \end{align*}\]
Exercise \(\PageIndex{3}\)
Divide:
\[ \frac{15}{7} \div 5\nonumber \]
Answer
-
\(\frac{3}{7}\)
After inverting, you may need to factor and cancel, as we learned to do in Section 4.2.
Example \(\PageIndex{4}\)
Divide −6/35 by 33/55.
Solution
Invert, multiply, factor, and cancel common factors.
\[ \begin{aligned} - \frac{6}{35} \div \frac{33}{55} = - \frac{6}{35} \cdot \frac{55}{33} ~ & \textcolor{red}{ \text{ Invert the divisor (second number).}} \\ = - \frac{6 \cdot 55}{35 \cdot 33} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ = - \frac{(2 \cdot 3) \cdot (5 \cdot 11)}{(5 \cdot 7) \cdot (3 \cdot 11)} ~ & \textcolor{red}{ \text{ Factor numerators and denominators.}} \\ = - \frac{2 \cdot \cancel{3} \cdot \cancel{5} \cdot \cancel{11}}{ \cancel{5} \cdot 7 \cdot \cancel{3} \cdot \cancel{11}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = - \frac{2}{7} ~ & \textcolor{red}{ \text{ Remaining factors.}} \end{aligned}\nonumber \]
Note that unlike signs produce a negative answer.
Exercise \(\PageIndex{4}\)
Divide:
\[ \frac{6}{15} \div \left( - \frac{42}{35} \right)\nonumber \]
- Answer
-
-1/3
Of course, you can also choose to factor numerators and denominators in place, then cancel common factors.
Exercises
Find the reciprocal of the given number.
1. 16/5
2. −17
3. −15/16
4. 30
Determine which property of multiplication is depicted by the given identity.
5. \( \frac{−19}{12} \cdot 1 = \frac{−19}{12}\)
6. \(− \frac{4}{1} \cdot \left( − \frac{1}{4} \right) = 1\)
Divide the fractions and simplify your result.
7. \(\frac{8}{23} \div \frac{−6}{11}\)
8. \(\frac{−10}{21} \div \frac{−6}{5}\)
9. \(\frac{5}{9} \div \frac{4}{3}\)
10. \(\frac{−2}{7} \div \frac{−8}{7}\)
11. \(\frac{20}{17} \div 5\)
12. \(−6 \div \frac{−21}{8}\)
13. \(\frac{3}{4} \div (−9)\)
Answers
1. \(\frac{5}{16}\)
2. \(− \frac{1}{17}\)
3. \(− \frac{16}{15}\)
4. \(\frac{1}{30}\)
5. multiplicative identity property
6. multiplicative inverse property
7. \(− \frac{44}{69}\)
8. \(\frac{25}{63}\)
9. \( \frac{5}{12}\)
10. \(\frac{1}{4}\)
11. \(\frac{4}{17}\)
12. \(\frac{16}{7}\)
13. \(− \frac{1}{12}\)


