3.4: Dividing Decimals

Last updated

Mar 21, 2024
Save as PDF
- 3.3: Multiplying Decimals
- 4: Introduction to Algebra

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

In this and following sections we make use of the terms divisor, dividend, quotient, and remainder.

Divisor, Dividend, Quotient, and Remainder

This schematic reminds readers of the position of these terms in the division process.

$Screen Shot 2019-09-11 at 1.05.57 PM.png$

Now that these terms are defined, we begin the discussion of division of decimal numbers. Suppose that we wish to divide 637 by 100. We could do this in fraction form, change the result to a mixed fraction, then the mixed fraction to decimal form.

$\frac{637}{100} = 6 \frac{37}{100} = 6.37\nonumber$

We can also arrange the division much as we would the division of two whole numbers.

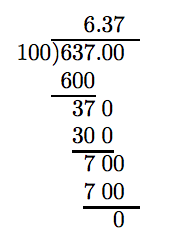
$Screen Shot 2019-09-11 at 1.10.16 PM.png$

Note that adding two zeros after the decimal point in the dividend does not change the value of 637. Further, note that we proceed as if we are dividing two whole numbers, placing the decimal point in the quotient directly above the decimal point in the dividend.

These observations lead to the following algorithm.

Dividing a Decimal by a Whole Number

To divide a decimal number by a whole number, proceed as follows:

Set up the long division as you would the division of two whole numbers.
Perform the division as if the numbers were both whole numbers, adding zeros to the right of the decimal point in the dividend as necessary to complete the division.
Place the decimal point in the quotient immediately above the decimal point in the dividend.

Example 1

Divide 23 by 20.

Solution

Arrange as if using long division to divide whole numbers, adding enough zeros to the right of the decimal point in the dividend to complete the division.

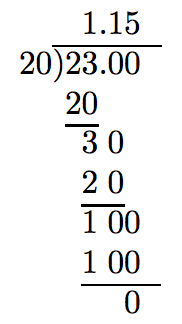
$Screen Shot 2019-09-11 at 1.13.53 PM.png$

Hence, 23 divided by 20 is 1.15.

Adding Zeroes to the Right of the Decimal Point

Usually, one does not immediately see how many zeros to the right of the decimal point in the dividend are needed. These zeros are usually added at each step of the division, until the division is completed or the user is willing to terminate the process and accept only an estimate of the quotient.

Example 2

Divide: 155.2 ÷ 25.

Solution

Arrange as if using long division to divide whole numbers, and begin.

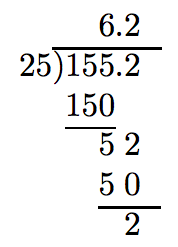
$Screen Shot 2019-09-11 at 1.14.00 PM.png$

We still have a nonzero remainder. Adding another zero does no good.

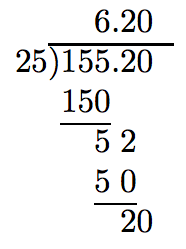
$Screen Shot 2019-09-11 at 1.14.05 PM.png$

However, if we add one more additional zero, the division completes with a zero remainder.

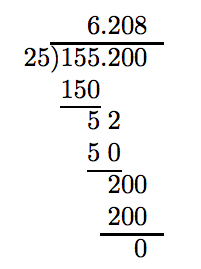
$Screen Shot 2019-09-11 at 1.17.55 PM.png$

Thus, 155.2 divided by 25 is 6.208.

Exercise

Divide: 42.55 ÷ 23

Answer: 1.85

Decimal Divisors When the divisor contains a decimal point, we have a little work to do before we begin the division process. Suppose that we wish to divide 1.25 by 2.5. In fraction form, we could start with

$\frac{1.25}{2.5},\nonumber$

then clear the decimals from the denominator by multiplying both numerator and denominator by 10. Note: Recall that multiplying by 10 moves the decimal point one place to the right.

$\begin{aligned} \frac{1.25}{2.5} = \frac{1.25 \cdot 10}{2.5 \cdot 10} \\ = \frac{12.5}{25} \end{aligned}\nonumber$

Thus, dividing 1.25 by 2.5 is equivalent to dividing 12.5 by 25. This we know how to do.

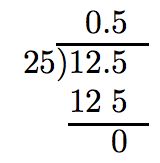
$Screen Shot 2019-09-11 at 1.22.03 PM.png$

Thus, 1.25 divided by 2.5 is 0.5.

Writing Mathematics

Never write .5. Always add the leading zero in the ones place and write 0.5.

Instead of working in fraction form, we can take care of positioning the decimal point in the long division framework. Start with:

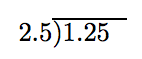
$Screen Shot 2019-09-11 at 1.23.54 PM.png$

Move the decimal point in the divisor to the end of the divisor, then move the decimal point in the dividend an equal number of places.

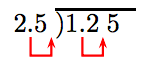
$Screen Shot 2019-09-11 at 1.23.57 PM.png$

Thus, the division becomes

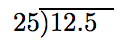
$Screen Shot 2019-09-11 at 1.24.03 PM.png$

and we proceed as above to find the quotient. This discussion motivates the following algorithm.

Dividing by a Decimal Divisor

If the divisor contains a decimal, proceed as follows:

Move the decimal to the end of the divisor.
Move the decimal in the dividend an equal number of places.

We can then complete the division using the rules for dividing a decimal by a whole number.

Example 3

Divide: $\overline{ )4.392}$

Solution

Move the decimal in the divisor to the end of the divisor. Move the decimal in the dividend an equal number of places (two places) to the right.

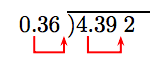
$Screen Shot 2019-09-11 at 1.30.09 PM.png$

Now we can follow the algorithm for dividing a decimal number by a whole number.

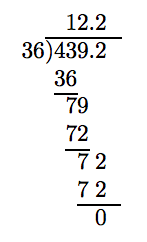
$Screen Shot 2019-09-11 at 1.30.15 PM.png$

Thus, 4.392 divided by 0.36 is 12.2.

Exercise

Divide: $0.45 \overline{)36.99}$

Answer: 82.2

Dividing Signed Decimal Numbers

The rules governing division of signed decimal numbers are identical to the rules governing division of integers.

Like Signs. The quotient of two decimal numbers with like signs is positive. That is:

$\frac{(+)}{(+)} = + \text{ and } \frac{(−)}{(−)} = +\nonumber$

Unlike Signs. The quotient of two decimal numbers with unlike signs is negative. That is:

$\frac{(+)}{(−)} = − \text{ and } \frac{(−)}{(+)} = −\nonumber$

Example 4

Divide: −0.03 ÷ 0.024.

Solution

First, divide the magnitudes. Move the decimal in the divisor to the end of the divisor. Move the decimal in the dividend an equal number of places (three places) to the right. Note that this requires an extra trailing zero in the dividend.

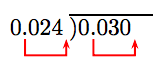
$Screen Shot 2019-09-11 at 1.46.22 PM.png$

Our problem then becomes:

\[ 24 \overline{24 )30}\)

We can now follow the algorithm for dividing a decimal number by a whole number. Note that we have to add two trailing zeros in the dividend to complete the division with a zero remainder.

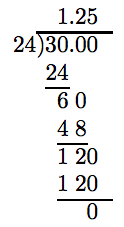
$Screen Shot 2019-09-11 at 1.46.30 PM.png$

Finally, because the quotient of unlike signs is negative, −0.03 divided by 0.024 is −1.25. That is,

$\frac{-0.03}{0.024} = -1.25.\nonumber$

Exercise

Divide: −0.0113 ÷ 0.05

Answer: −0.226

Rounding

Sometimes an exact decimal representation of a fraction is not needed and is an approximation is more than adequate.

Example 5

Convert 4/7 to a decimal. Round your answer to the nearest hundredth.

Solution

We need to carry the division one place beyond the hundredths place.

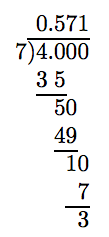
$Screen Shot 2019-09-11 at 1.50.40 PM.png$

To round to the nearest hundredth, first identify the rounding and test digits.

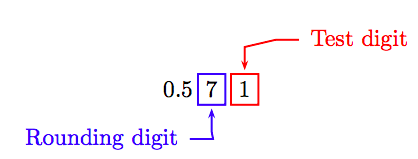
$Screen Shot 2019-09-11 at 1.50.45 PM.png$

Because the “test digit” is less 5, leave the rounding digit alone and truncate. Therefore, correct to the nearest hundredth, 4/7 ≈ 0.57.

Exercise

Convert 5/7 to a decimal. Round your answer to the nearest hundredth.

Answer: 0.71

Exercises

Divide the numbers.

1. $\frac{39}{52}$

7. $\frac{32.12}{73}$

13. $\frac{17}{25}$

19. $\frac{1.694}{2.2}$

25. $\frac{2.958}{−0.2}$

33. $\frac{1.248}{0.52}$

65. $\frac{−524.35}{100}$

77. Compute the quotient 47/3, and round your answer to the nearest tenth.

87. Compute the quotient 8/14, and round your answer to the nearest hundredth.

113. Media mail. To promote her business, Theresa mails several packages via Media Mail. One package weighing 2 lbs. costs $2.77, another package weighing 3 lbs. costs $3.16, and the third package weighing 5 lbs. costs $3.94 to mail. What was the average cost per pound to mail the packages? Round your result to the nearest penny. www.usps.com/prices/media-mailprices.htm

Answers

1. 0.75

7. 0.44

13. 0.68

19. 0.77

25. −14.79

33. 2.4

65. −5.2435

77. 15.7

87. 0.57

113. $0.99 per pound

Search

Text Color

Text Size

Margin Size

Font Type

Dividing Signed Decimal Numbers

Rounding

Exercises

Answers

Support Center

How can we help?