9.E: Sequences and Series (Exercises)

Last updated
Save as PDF

Page ID: 3821

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

9.1: Sequences

In exercises 1 - 4, find the first six terms of each sequence, starting with $ n=1$.

1) $a_n=1+(−1)^n$ for $ n≥1$

Answer: $ a_n=0$ if $ n$ is odd and $ a_n=2$ if $ n$ is even

2) $ a_n=n^2−1$ for $ n≥1$

3) $ a_1=1$ and $ a_n=a_{n−1}+n$ for $ n≥2$

Answer: $ {a_n}={1,3,6,10,15,21,…}$

4) $ a_1=1, a_2=1$ and $ a_n+2=a_n+a_{n+1}$ for $ n≥1$

5) Find an explicit formula for $ a_n$ where $ a_1=1$ and $ a_n=a_{n−1}+n$ for $ n≥2$.

Answer: $ a_n=\dfrac{n(n+1)}{2}$

6) Find a formula $ a_n$ for the $n^{\text{th}}$ term of the arithmetic sequence whose first term is $ a_1=1$ such that $ a_{n−1}−a_n=17$ for $ n≥1$.

7) Find a formula $ a_n$ for the $n^{\text{th}}$ term of the arithmetic sequence whose first term is $ a_1=−3$ such that $ a_{n−1}−a_n=4$ for $ n≥1$.

Answer: $ a_n=4n−7$

8) Find a formula $ a_n$ for the $n^{\text{th}}$ term of the geometric sequence whose first term is $ a_1=1$ such that $ \dfrac{a_{n+1}}{a_n}=10$ for $ n≥1$.

9) Find a formula $ a_n$ for the $n^{\text{th}}$ term of the geometric sequence whose first term is $ a_1=3$ such that $ \dfrac{a_{n+1}}{a_n}=1/10$ for $ n≥1$.

Answer: $ a_n=3.10^{1−n}=30.10^{−n}$

10) Find an explicit formula for the $n^{\text{th}}$ term of the sequence whose first several terms are $ {0,3,8,15,24,35,48,63,80,99,…}.$ (Hint: First add one to each term.)

11) Find an explicit formula for the $n^{\text{th}}$ term of the sequence satisfying $ a_1=0$ and $ a_n=2a_{n−1}+1$ for $ n≥2$.

Answer: $ a_n=2^n−1$

In exercises 12 and 13, find a formula for the general term $ a_n$ of each of the following sequences.

12) $ {1,0,−1,0,1,0,−1,0,…}$ (Hint: Find where $\sin x$ takes these values)

13) $ {1,−1/3,1/5,−1/7,…}$

Answer: $ a_n=\dfrac{(−1)^{n−1}}{2n−1}$

In exercises 14-18, find a function $ f(n)$ that identifies the $n^{\text{th}}$ term $ a_n$ of the following recursively defined sequences, as $ a_n=f(n)$.

14) $ a_1=1$ and $ a_{n+1}=−a_n$ for $ n≥1$

15) $ a_1=2$ and $ a_{n+1}=2a_n$ for $ n≥1$

Answer: $ f(n)=2^n$

16) $ a_1=1$ and $ a_{n+1}=(n+1)a_n$ for $ n≥1$

17) $ a_1=2$ and $ a_{n+1}=(n+1)a_n/2$ for $ n≥1$

Answer: $f(n)=\dfrac{n!}{2^{n-2}}$

18) $ a_1=1$ and $ a_{n+1}=a_n/2^n$ for $ n≥1$

In exercises 19 - 22, plot the first $ N$ terms of the given sequence. State whether the graphical evidence suggests that the sequence converges or diverges.

19) [T] $ a_1=1, a_2=2$, and for $ n≥2, a_n=\frac{1}{2}(a_{n−1}+a_{n−2})$; $ N=30$

Answer

Terms oscillate above and below $ 5/3$ and appear to converge to $ 5/3$.

$This is a graph of an oscillating sequence. Terms oscillate above and below 5/3 and seem to converge to 5/3.$

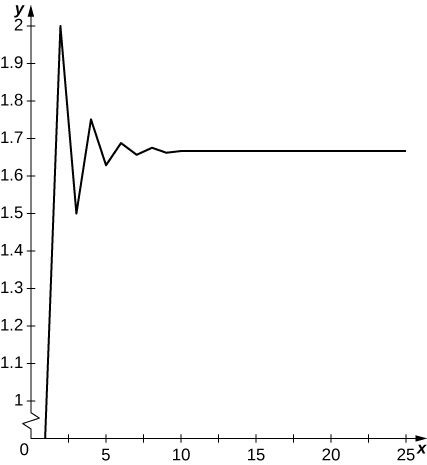
20) [T] $ a_1=1, a_2=2, a_3=3$ and for $ n≥4, a_n=\frac{1}{3}(a_{n−1}+a_{n−2}+a_{n−3}), N=30$

21) [T] $ a_1=1, a_2=2$, and for $ n≥3, a_n=\sqrt{a_{n−1}a_{n−2}}; N=30$

Answer

Terms oscillate above and below $ y≈1.57..$ and appear to converge to a limit.

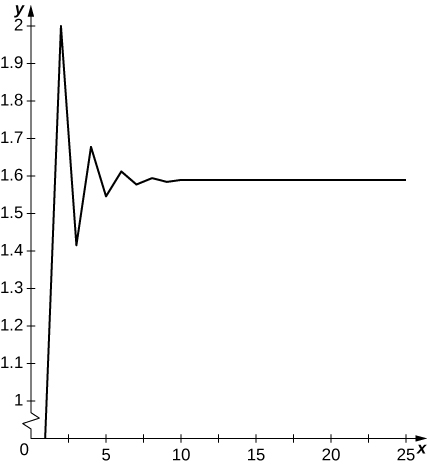
$This is a graph of the oscillating sequence. Terms oscillate above and below y = 1.57 and seem to converse to 1.57.$

22) [T] $ a_1=1, a_2=2, a_3=3$, and for $ n≥4, a_n=\sqrt{a_{n−1}a_{n−2}a_{n−3}}; N=30$

In exercises 23 - 16, suppose that $\displaystyle \lim_{n→∞}a_n=1, $ $\displaystyle \lim_{n→∞}b_n=−1$, and $ 0<−b_n<a_n$ for all $ n$.

Using this information, evaluate each of the following limits, state that the limit does not exist, or state that there is not enough information to determine whether the limit exists.

23) $\displaystyle \lim_{n→∞}3a_n−4b_n$

Answer: $\displaystyle \lim_{n→∞}3a_n−4b_n \quad = \quad 7$

24) $\displaystyle \lim_{n→∞}\frac{1}{2}b_n−\frac{1}{2}a_n$

25) $\displaystyle \lim_{n→∞}\frac{a_n+b_n}{a_n−b_n}$

Answer: $\displaystyle \lim_{n→∞}\frac{a_n+b_n}{a_n−b_n} \quad = \quad 0$

26) $\displaystyle \lim_{n→∞}\frac{a_n−b_n}{a_n+b_n}$

In exercises 27 - 30, find the limit of each of the following sequences, using L’Hôpital’s rule when appropriate.

27) $ \dfrac{n^2}{2^n}$

Answer: $\displaystyle \lim_{n→∞} \dfrac{n^2}{2^n} \quad = \quad 0$

28) $ \dfrac{(n−1)^2}{(n+1)^2}$

29) $ \dfrac{\sqrt{n}}{\sqrt{n+1}}$

Answer: $\displaystyle \lim_{n→∞} \dfrac{\sqrt{n}}{\sqrt{n+1}} \quad = \quad 1 $

30) $ n^{1/n}$ (Hint: $ n^{1/n}=e^{\frac{1}{n}\ln n})$

In exercises 31 - 37, state whether each sequence is bounded and whether it is eventually monotone, increasing, or decreasing.

31) $ n/2^n, n≥2$

Answer: bounded, decreasing for $ n≥1$

32) $ \ln(1+\dfrac{1}{n})$

33) $ \sin n$

Answer: bounded, not monotone

34) $ \cos(n^2)$

35) $ n^{1/n}, \quad n≥3$

Answer: bounded, decreasing

36) $ n^{−1/n}, \quad n≥3$

37) $ \tan n$

Answer: not monotone, not bounded

In exercises 38 - 39, determine whether the given sequence has a limit. If it does, find the limit.

38) $ a_1=\sqrt{2}, a_2=\sqrt{2\sqrt{2}}. a_3=\sqrt{2\sqrt{2\sqrt{2}}}$ etc.

39) $ a_1=3, a_n=\sqrt{2a_{n−1}}, n=2,3,….$

Answer: $ a_n$ is decreasing and bounded below by $2$. The limit a must satisfy $ a=\sqrt{2a}$ so $ a=2$, independent of the initial value.

Use the Squeeze Theorem to find the limit of each sequence in exercises 40 - 43.

40) $ n\sin(1/n)$

41) $ \dfrac{\cos(1/n)−1}{1/n}$

Answer: $0$

42) $ a_n=\dfrac{n!}{n^n}$

43) $ a_n=\sin n \sin(1/n)$

Answer: $ 0$ since $|\sin x|≤|x|$ and $ |\sin x|≤1$ so $ −\dfrac{1}{n}≤a_n≤\dfrac{1}{n})$.

For the sequences in exercises 44 and 45, plot the first $ 25$ terms of the sequence and state whether the graphical evidence suggests that the sequence converges or diverges.

44) [T] $ a_n=\sin n$

45) [T] $ a_n=\cos n$

Answer

Graph oscillates and suggests no limit.

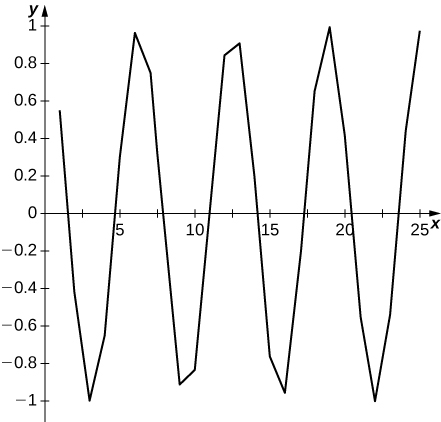
$This is a graph that oscillates between 1 and -1 from 0 to 25 on the x axis. There appears to be no limit.$

In exercises 46 - 52, determine the limit of the sequence or show that the sequence diverges. If it converges, find its limit.

46) $ a_n=tan^{−1}(n^2)$

47) $ a_n=(2n)^{1/n}−n^{1/n}$

Answer: $ n^{1/n}→1$ and $ 2^{1/n}→1,$ so $ a_n→0$

48) $ a_n=\dfrac{ln(n^2)}{ln(2n)}$

49) $ a_n=\left(1−\frac{2}{n}\right)^n$

Answer: Since $ (1+1/n)^n→e$, one has $ (1−2/n)^n≈(1+k)^{−2k}→e^{−2}$ as $ k→∞.$

50) $ a_n=\ln\left(\dfrac{n+2}{n^2−3}\right)$

51) $ a_n=\dfrac{2^n+3^n}{4^n}$

Answer: $ 2^n+3^n≤2⋅3^n$ and $ 3^n/4^n→0$ as $ n→∞$, so $ a_n→0$ as $ n→∞.$

52) $ a_n=\dfrac{(1000)^n}{n!}$

53) $ a_n=\dfrac{(n!)^2}{(2n)!}$

Answer: $ \dfrac{a_{n+1}}{a_n}=n!/(n+1)(n+2)⋯(2n) =\dfrac{1⋅2⋅3⋯n}{(n+1)(n+2)⋯(2n)}<1/2^n$. In particular, $ a_{n+1}/a_n≤1/2$, so $ a_n→0$ as $ n→∞$.

Newton’s method seeks to approximate a solution $ f(x)=0$ that starts with an initial approximation $ x_0$ and successively defines a sequence $ x_{n+1}=x_n−\dfrac{f(x_n)}{f′(x_n)}$. For the given choice of $ f$ and $ x_0$, write out the formula for $ x_{n+1}$. If the sequence appears to converge, give an exact formula for the solution $ x$, then identify the limit $ x$ accurate to four decimal places and the smallest $ n$ such that $ x_n$ agrees with $ x$ up to four decimal places.

54) [T] $ f(x)=x^2−2, x_0=1$

55) [T] $ f(x)=(x−1)^2−2, x_0=2$

Answer: $ x_{n+1}=x_n−((x_n−1)^2−2)/2(x_n−1);
x=1+\sqrt{2}, x≈2.4142, n=5$

56) [T] $ f(x)=e^x−2, x_0=1$

57) [T] $ f(x)=lnx−1, x_0=2$

Answer: $ x_{n+1}=x_n−x_n(ln(x_n)−1);
x=e, x≈2.7183, n=5$

58) [T] Suppose you start with one liter of vinegar and repeatedly remove $ 0.1L$, replace with water, mix, and repeat.

a. Find a formula for the concentration after $ n$ steps.

b. After how many steps does the mixture contain less than $ 10%$ vinegar?

59) [T] A lake initially contains $ 2000$ fish. Suppose that in the absence of predators or other causes of removal, the fish population increases by $ 6%$ each month. However, factoring in all causes, $ 150$ fish are lost each month.

a. Explain why the fish population after $ n$ months is modeled by $ P_n=1.06P_{n−1}−150$ with $ P_0=2000$.

b. How many fish will be in the pond after one year?

Answer: a. Without losses, the population would obey $ P_n=1.06P_{n−1}$. The subtraction of $ 150$ accounts for fish losses.
b. After $ 12$ months, we have $ P_{12}≈1494.$

60) [T] A bank account earns $ 5%$ interest compounded monthly. Suppose that $ $1000$ is initially deposited into the account, but that $ $10$ is withdrawn each month.

a. Show that the amount in the account after $ n$ months is $ A_n=(1+.05/12)A_{n−1}−10; A_0=1000.$

b. How much money will be in the account after $ 1$ year?

c. Is the amount increasing or decreasing?

d. Suppose that instead of $ $10$, a fixed amount $ d$ dollars is withdrawn each month. Find a value of $ d$ such that the amount in the account after each month remains $ $1000$.

e. What happens if $ d$ is greater than this amount?

61) [T] A student takes out a college loan of $ $10,000$ at an annual percentage rate of $ 6%,$ compounded monthly.

a. If the student makes payments of $ $100$ per month, how much does the student owe after $ 12$ months?

b. After how many months will the loan be paid off?

Answer: a. The student owes $ $9383$ after $ 12$ months.
b. The loan will be paid in full after $ 139$ months or eleven and a half years.

62) [T] Consider a series combining geometric growth and arithmetic decrease. Let $ a_1=1$. Fix $ a>1$ and $ 0<b<a$. Set $ a_{n+1}=a.a_n−b.$ Find a formula for $ a_{n+1}$ in terms of $ a_n, a$, and $ b$ and a relationship between $ a$ and $ b$ such that $ a_n$ converges.

63) [T] The binary representation $ x=0.b_1b_2b_3...$ of a number $ x$ between $ 0$ and $ 1$ can be defined as follows. Let $ b_1=0$ if $ x<1/2$ and $ b_1=1$ if $ 1/2≤x<1.$ Let $ x_1=2x−b_1$. Let $ b_2=0$ if $ x_1<1/2$ and $ b_2=1$ if $ 1/2≤x<1$. Let $ x_2=2x_1−b_2$ and in general, $ x_n=2x_{n−1}−b_n$ and $ b_{n−}1=0$ if $ x_n<1/2$ and $ b_{n−1}=1$ if $ 1/2≤x_n<1$. Find the binary expansion of $ 1/3$.

Answer: $ b_1=0, x_1=2/3, b_2=1, x_2=4/3−1=1/3,$ so the pattern repeats, and $ 1/3=0.010101….$

64) [T] To find an approximation for $ π$, set $ a_0=\sqrt{2+1}, a_1=\sqrt{2+a_0}$, and, in general, $ a_{n+1}=\sqrt{2+a_n}$. Finally, set $ p_n=3.2^n\sqrt{2−a_n}$. Find the first ten terms of $ p_n$ and compare the values to $ π$.

For the following two exercises, assume that you have access to a computer program or Internet source that can generate a list of zeros and ones of any desired length. Pseudo-random number generators (PRNGs) play an important role in simulating random noise in physical systems by creating sequences of zeros and ones that appear like the result of flipping a coin repeatedly. One of the simplest types of PRNGs recursively defines a random-looking sequence of $ N$ integers $ a_1,a_2,…,a_N$ by fixing two special integers $ (K$ and $ M$ and letting $ a_{n+1}$ be the remainder after dividing $ K.a_n$ into $ M$, then creates a bit sequence of zeros and ones whose $n^{\text{th}}$ term $ b_n$ is equal to one if $ a_n$ is odd and equal to zero if $ a_n$ is even. If the bits $ b_n$ are pseudo-random, then the behavior of their average $ (b_1+b_2+⋯+b_N)/N$ should be similar to behavior of averages of truly randomly generated bits.

65) [T] Starting with $ K=16,807$ and $ M=2,147,483,647$, using ten different starting values of $ a_1$, compute sequences of bits $ b_n$ up to $ n=1000,$ and compare their averages to ten such sequences generated by a random bit generator.

Answer: For the starting values $ a_1=1, a_2=2,…, a_1=10,$ the corresponding bit averages calculated by the method indicated are $ 0.5220, 0.5000, 0.4960, 0.4870, 0.4860, 0.4680, 0.5130, 0.5210, 0.5040,$ and $ 0.4840$. Here is an example of ten corresponding averages of strings of $ 1000$ bits generated by a random number generator: $ 0.4880, 0.4870, 0.5150, 0.5490, 0.5130, 0.5180, 0.4860, 0.5030, 0.5050, 0.4980.$ There is no real pattern in either type of average. The random-number-generated averages range between $ 0.4860$ and $ 0.5490$, a range of $ 0.0630$, whereas the calculated PRNG bit averages range between $ 0.4680$ and $ 0.5220$, a range of $ 0.0540.$

66) [T] Find the first $ 1000$ digits of $ π$ using either a computer program or Internet resource. Create a bit sequence $ b_n$ by letting $ b_n=1$ if the $n^{\text{th}}$ digit of $ π$ is odd and $ b_n=0$ if the $n^{\text{th}}$ digit of $ π$ is even. Compute the average value of $ b_n$ and the average value of $ d_n=|b_{n+1}−b_n|, n=1,...,999.$ Does the sequence $ b_n$ appear random? Do the differences between successive elements of $ b_n$ appear random?

9.2: Infinite Series

In exercises 1 - 4, use sigma notation to write each expressions as an infinite series.

1) $1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+⋯$

Answer: $\displaystyle \sum_{n=1}^∞\frac{1}{n}$

2) $ 1−1+1−1+⋯$

3) $ 1−\frac{1}{2}+\frac{1}{3}−\frac{1}{4}+...$

Answer: $\displaystyle \sum_{n=1}^∞\frac{(−1)^{n−1}}{n}$

4) $ \sin 1+\sin \frac{1}{2}+\sin \frac{1}{3}+\sin \frac{1}{4}+⋯$

In exercises 5 - 8, compute the first four partial sums $ S_1,…,S_4$ for the series having $ n^{\text{th}}$ term $ a_n$ starting with $ n=1$ as follows.

5) $ a_n=n$

Answer: $ 1,3,6,10$

6) $ a_n=1/n$

7) $ a_n=\sin \frac{nπ}{2}$

Answer: $ 1,1,0,0$

8) $ a_n=(−1)^n$

In exercises 9 - 12, compute the general term $ a_n$ of the series with the given partial sum $ S_n$. If the sequence of partial sums converges, find its limit $ S$.

9) $ S_n=1−\frac{1}{n}, \quad n≥2$

Answer: $ a_n=S_n−S_{n−1}=\dfrac{1}{n−1}−\dfrac{1}{n}.$ Since $\displaystyle S = \lim_{n\to\infty} S_n = \lim_{n\to\infty} \left(1−\frac{1}{n}\right) = 1,$ the series converges to $ S=1.$

10) $ S_n=\dfrac{n(n+1)}{2}, \quad n≥1$

11) $ S_n=\sqrt{n},\quad n≥2$

Answer: $ a_n=S_n−S_{n−1}=\sqrt{n}−\sqrt{n−1}=\dfrac{1}{\sqrt{n−1}+\sqrt{n}}.$
The series diverges because the partial sums are unbounded.
That is, $\displaystyle \lim_{n\to\infty} S_n = \lim_{n\to\infty} \sqrt{n} = \infty.$

12) $ S_n=2−\dfrac{n+2}{2^n},\quad n≥1$

For each series in exercises 13 - 16, use the sequence of partial sums to determine whether the series converges or diverges.

13) $\displaystyle \sum_{n=1}^∞\frac{n}{n+2}$

Answer: $ S_1=1/3,$
$ S_2=1/3+2/4>1/3+1/3=2/3,$
$S_3=1/3+2/4+3/5>3⋅(1/3)=1.$
In general $ S_k>k/3,$ so the series diverges.
Note that the $n^{\text{th}}$ Term Test for Divergence could also be used to prove that this series diverges.

14) $\displaystyle \sum_{n=1}^∞(1−(−1)^n))$

15) $\displaystyle \sum_{n=1}^∞\frac{1}{(n+1)(n+2)}$ (Hint: Use a partial fraction decomposition like that for $\displaystyle \sum_{n=1}^∞\frac{1}{n(n+1)}.)$

Answer

$ S_1=1/(2\cdot 3)=1/6=2/3−1/2,$

$ S_2=1/(2\cdot 3)+1/(3\cdot 4)=2/12+1/12=1/4=3/4−1/2,$

$ S_3=1/(2\cdot 3)+1/(3\cdot 4)+1/(4\cdot 5)=10/60+5/60+3/60=3/10=4/5−1/2,$

$ S_4=1/(2\cdot 3)+1/(3\cdot 4)+1/(4\cdot 5)+1/(5\cdot 6)=10/60+5/60+3/60+2/60=1/3=5/6−1/2.$

The pattern is $ S_k=\dfrac{k+1}{k+2}−\dfrac{1}{2}.$
Then $\displaystyle \lim_{n\to\infty} S_n = \lim_{n\to\infty} \left( \dfrac{k+1}{k+2}−\dfrac{1}{2} \right) = \dfrac{1}{2},$ so the series converges to $ 1/2.$

16) $\displaystyle \sum_{n=1}^∞\frac{1}{2n+1}$ (Hint: Follow the reasoning for $\displaystyle \sum_{n=1}^∞\frac{1}{n}.)$

Suppose that $\displaystyle \sum_{n=1}^∞a_n=1$, that $\displaystyle \sum_{n=1}^∞b_n=−1$, that $ a_1=2$, and $ b_1=−3$. Use this information to find the sum of the indicated series in exercises 17 - 20.

17) $\displaystyle \sum_{n=1}^∞(a_n+b_n)$

Answer: $ \displaystyle \sum_{n=1}^∞(a_n+b_n) \quad = \quad \sum_{n=1}^∞ a_n + \sum_{n=1}^∞ b_n \quad = \quad 1 + (-1) \quad = \quad 0$

18) $\displaystyle \sum_{n=1}^∞(a_n−2b_n)$

19) $\displaystyle \sum_{n=2}^∞(a_n−b_n)$

Answer: $\displaystyle \sum_{n=2}^∞(a_n−b_n) \quad = \quad \sum_{n=2}^∞ a_n - \sum_{n=2}^∞ b_n \quad = \quad \left(\sum_{n=1}^∞ a_n - a_1\right) - \left(\sum_{n=1}^∞ b_n -b_1\right) \quad = \quad (1 - 2) - (-1 - (-3)) = -1 - 2 \quad = \quad -3$

20) $\displaystyle \sum_{n=1}^∞(3a_{n+1}−4b_{n+1})$

In exercises 21 - 26, state whether the given series converges or diverges and explain why.

21) $\displaystyle \sum_{n=1}^∞\frac{1}{n+1000}$ (Hint: Rewrite using a change of index.)

Answer: The series diverges, $\displaystyle \sum_{n=1001}^∞\frac{1}{n}$

22) $\displaystyle \sum_{n=1}^∞\frac{1}{n+10^{80}}$ (Hint: Rewrite using a change of index.)

23) $ 1+\frac{1}{10}+\frac{1}{100}+\frac{1}{1000}+⋯$

Answer: This is a convergent geometric series, since $ r=\frac{1}{10}<1$

24) $ 1+\frac{e}{π}+\frac{e^2}{π^2}+\frac{e^3}{π^3}+⋯$

25) $ 1+\frac{π}{e^2}+\frac{π^2}{e^4}+\frac{π^3}{e^6}+\frac{π^4}{e^8}+⋯$

Answer: This is a convergent geometric series, since $ r=π/e^2<1$

26) $ 1−\sqrt{\frac{π}{3}}+\sqrt{\frac{π^2}{9}}−\sqrt{\frac{π^3}{27}}+⋯$

For each $ a_n$ in exercises 27 - 30, write its sum as a geometric series of the form $\displaystyle \sum_{n=1}^∞ar^n$. State whether the series converges and if it does, find the exact value of its sum.

27) $ a_1=−1$ and $ \dfrac{a_n}{a_{n+1}}=−5$ for $ n≥1.$

Answer: $\displaystyle \sum_{n=1}^∞5⋅(−1/5)^n$, converges to $ −5/6$

28) $ a_1=2$ and $ \dfrac{a_n}{a_{n+1}}=1/2$ for $ n≥1.$

29) $ a_1=10$ and $ \dfrac{a_n}{a_{n+1}}=10$ for $ n≥1$.

Answer: $\displaystyle \sum_{n=1}^∞100⋅(1/10)^n,$ converges to $\frac{100}{9}$

30) $ a_1=\frac{1}{10}$ and $ a_n/a_{n+1}=−10$ for $ n≥1$.

In exercises 31 - 34, use the identity $\displaystyle \frac{1}{1−y}=\sum_{n=0}^∞y^n$ (which is true for $|y| < 1$) to express each function as a geometric series in the indicated term.

31) $ \dfrac{x}{1+x}$ in $ x$

Answer: $\displaystyle x\sum_{n=0}^∞(−x)^n=\sum_{n=1}^∞(−1)^{n−1}x^n$

32) $ \dfrac{\sqrt{x}}{1−x^{3/2}}$ in $ \sqrt{x}$

33) $ \dfrac{1}{1+\sin^2x}$ in $\sin x$

Answer: $\displaystyle \sum_{n=0}^∞(−1)^n\sin^{2n}(x)$

34) $ \sec^2 x$ in $\sin x$

In exercises 35 - 38, evaluate the telescoping series or state whether the series diverges.

35) $\displaystyle \sum_{n=1}^∞2^{1/n}−2^{1/(n+1)}$

Answer: $ S_k=2−2^{1/(k+1)}→1$ as $ k→∞.$

36) $\displaystyle \sum_{n=1}^∞\frac{1}{n^{13}}−\frac{1}{(n+1)^{13}}$

37) $\displaystyle \sum_{n=1}^∞(\sqrt{n}−\sqrt{n+1})$

Answer: $ S_k=1−\sqrt{k+1}$ diverges

38) $\displaystyle \sum_{n=1}^∞(\sin n−\sin(n+1))$

Express each series in exercises 39 - 42 as a telescoping sum and evaluate its $n^{\text{th}}$ partial sum.

39) $\displaystyle \sum_{n=1}^∞\ln\left(\frac{n}{n+1}\right)$

Answer: $\displaystyle \sum_{n=1}^∞[\ln n−\ln(n+1)],$
$S_k=−\ln(k+1)$

40) $\displaystyle \sum_{n=1}^∞\frac{2n+1}{(n^2+n)^2}$ (Hint: Factor denominator and use partial fractions.)

41) $\displaystyle \sum_{n=2}^∞\frac{\ln\left(1+\frac{1}{n}\right)}{(\ln n)\ln(n+1)}$

Answer: $ a_n=\frac{1}{\ln n}−\frac{1}{\ln(n+1)}$ and $ S_k=\frac{1}{\ln(2)}−\frac{1}{\ln(k+1)}→\frac{1}{\ln(2)}$

42) $\displaystyle \sum_{n=1}^∞\frac{(n+2)}{n(n+1)2^{n+1}}$ (Hint: Look at $ 1/(n2^n)$.

A general telescoping series is one in which all but the first few terms cancel out after summing a given number of successive terms.

43) Let $ a_n=f(n)−2f(n+1)+f(n+2),$ in which $ f(n)→0$ as $ n→∞.$ Find $\displaystyle \sum_{n=1}^∞a_n$.

Answer: $\displaystyle \sum_{n=1}^∞a_n=f(1)−f(2)$

44) $ a_n=f(n)−f(n+1)−f(n+2)+f(n+3),$ in which $ f(n)→0$ as $ n→∞$. Find $\displaystyle \sum_{n=1}^∞a_n$.

45) Suppose that $ a_n=c_0f(n)+c_1f(n+1)+c_2f(n+2)+c_3f(n+3)+c_4f(n+4),$ where $ f(n)→0$ as $ n→∞$. Find a condition on the coefficients $ c_0,…,c_4$ that make this a general telescoping series.

Answer: $ c_0+c_1+c_2+c_3+c_4=0$

46) Evaluate $\displaystyle \sum_{n=1}^∞\frac{1}{n(n+1)(n+2)}$ (Hint: $\displaystyle \frac{1}{n(n+1)(n+2)}=\frac{1}{2n}−\frac{1}{n+1}+\frac{1}{2(n+2)}$)

47) Evaluate $\displaystyle \sum_{n=2}^∞\frac{2}{n^3−n}.$

Answer: $\displaystyle \frac{2}{n^3−1}=\frac{1}{n−1}−\frac{2}{n}+\frac{1}{n+1},$
$S_n=(1−1+1/3)+(1/2−2/3+1/4) +(1/3−2/4+1/5)+(1/4−2/5+1/6)+⋯=1/2$

48) Find a formula for $\displaystyle \sum_{n=1}^∞\left(\frac{1}{n(n+N)}\right)$ where $ N$ is a positive integer.

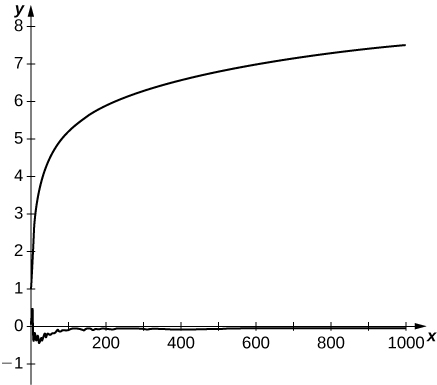
49) [T] Define a sequence $\displaystyle t_k=\sum_{n=1}^{k−1}(1/k)−\ln k$. Use the graph of $ 1/x$ to verify that $ t_k$ is increasing. Plot $ t_k$ for $ k=1…100$ and state whether it appears that the sequence converges.

Answer

$ t_k$ converges to $ 0.57721…t_k$ is a sum of rectangles of height $ 1/k$ over the interval $ [k,k+1]$ which lie above the graph of $ 1/x$.

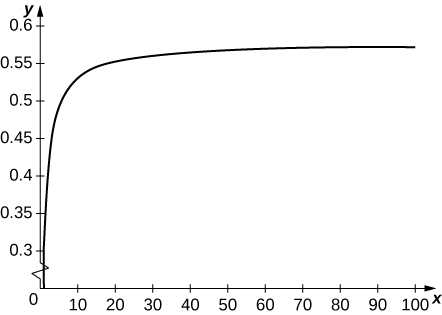
$This is a graph of a sequence in quadrant one that begins close to 0 and appears to converge to 0.57721.$

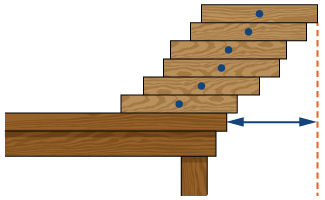
50) [T] Suppose that $ N$ equal uniform rectangular blocks are stacked one on top of the other, allowing for some overhang. Archimedes’ law of the lever implies that the stack of $ N$ blocks is stable as long as the center of mass of the top $ (N−1)$ blocks lies at the edge of the bottom block. Let $ x$ denote the position of the edge of the bottom block, and think of its position as relative to the center of the next-to-bottom block. This implies that $ (N−1)x=\left(\frac{1}{2}−x\right)$ or $ x=1/(2N)$. Use this expression to compute the maximum overhang (the position of the edge of the top block over the edge of the bottom block.) See the following figure.

$This is a diagram of the edge of a table with several blocks stacked on the edge. Each block is pushed slightly to the right, and over the edge of the table. An arrow is drawn with arrowheads at both ends from the edge of the table to a line drawn down from the edge of the highest block.$

Each of the following infinite series converges to the given multiple of $ π$ or $ 1/π$.

In each case, find the minimum value of $ N$ such that the $ Nth$ partial sum of the series accurately approximates the left-hand side to the given number of decimal places, and give the desired approximate value. Up to $ 15$ decimals place, $ π=3.141592653589793....$

51) [T] $\displaystyle π=−3+\sum_{n=1}^∞\frac{n2^nn!^2}{(2n)!},$ error $ <0.0001$

Answer: $N=22,$
$S_N=6.1415$

52) [T] $\displaystyle \frac{π}{2}=\sum_{k=0}^∞\frac{k!}{(2k+1)!!}=\sum_{k=0}^∞\frac{2^kk!^2}{(2k+1)!},$ error $ <10^{−4}$

53) [T] $\displaystyle \frac{9801}{2π}=\frac{4}{9801}\sum_{k=0}^∞\frac{(4k)!(1103+26390k)}{(k!)^4396^{4k}},$ error $ <10^{−12}$

Answer: $ N=3,$
$S_N=1.559877597243667...$

54) [T] $\displaystyle \frac{1}{12π}=\sum_{k=0}^∞\frac{(−1)^k(6k)!(13591409+545140134k)}{(3k)!(k!)^3640320^{3k+3/2}}$, error $ <10^{−15}$

55) [T] A fair coin is one that has probability $ 1/2$ of coming up heads when flipped.

a. What is the probability that a fair coin will come up tails $ n$ times in a row?

b. Find the probability that a coin comes up heads for the first time after an even number of coin flips.

Answer: a. The probability of any given ordered sequence of outcomes for $ n$ coin flips is $ 1/2^n$.
b. The probability of coming up heads for the first time on the $ n$ th flip is the probability of the sequence $ TT…TH$ which is $ 1/2^n$. The probability of coming up heads for the first time on an even flip is $\displaystyle \sum_{n=1}^∞1/2^{2n}$ or $ 1/3$.

56) [T] Find the probability that a fair coin is flipped a multiple of three times before coming up heads.

57) [T] Find the probability that a fair coin will come up heads for the second time after an even number of flips.

Answer: $5/9$

58) [T] Find a series that expresses the probability that a fair coin will come up heads for the second time on a multiple of three flips.

59) [T] The expected number of times that a fair coin will come up heads is defined as the sum over $ n=1,2,…$ of $ n$ times the probability that the coin will come up heads exactly $ n$ times in a row, or $ \dfrac{n}{2^{n+1}}$. Compute the expected number of consecutive times that a fair coin will come up heads.

Answer: $\displaystyle E=\sum_{n=1}^∞\frac{n}{2^{n+1}}=1,$ as can be shown using summation by parts

60) [T] A person deposits $ $10$ at the beginning of each quarter into a bank account that earns $ 4%$ annual interest compounded quarterly (four times a year).

a. Show that the interest accumulated after $ n$ quarters is $ $10(\frac{1.01^{n+1}−1}{0.01}−n).$

b. Find the first eight terms of the sequence.

c. How much interest has accumulated after $ 2$ years?

61) [T] Suppose that the amount of a drug in a patient’s system diminishes by a multiplicative factor $ r<1$ each hour. Suppose that a new dose is administered every $ N$ hours. Find an expression that gives the amount $ A(n)$ in the patient’s system after $ n$ hours for each $ n$ in terms of the dosage $ d$ and the ratio $ r$. (Hint: Write $ n=mN+k$, where $ 0≤k<N$, and sum over values from the different doses administered.)

Answer: The part of the first dose after $ n$ hours is $ dr^n$, the part of the second dose is $ dr^{n−N}$, and, in general, the part remaining of the $ m^{\text{th}}$ dose is $ dr^{n−mN}$, so $\displaystyle A(n)=\sum_{l=0}^mdr^{n−lN}=\sum_{l=0}^mdr^{k+(m−l)N}=\sum_{q=0}^mdr^{k+qN}=dr^k\sum_{q=0}^mr^{Nq}=dr^k\frac{1−r^{(m+1)N}}{1−r^N},\;\text{where}\,n=k+mN.$

62) [T] A certain drug is effective for an average patient only if there is at least $ 1$ mg per kg in the patient’s system, while it is safe only if there is at most $ 2$ mg per kg in an average patient’s system. Suppose that the amount in a patient’s system diminishes by a multiplicative factor of $ 0.9$ each hour after a dose is administered. Find the maximum interval $ N$ of hours between doses, and corresponding dose range $ d$ (in mg/kg) for this $ N$ that will enable use of the drug to be both safe and effective in the long term.

63) Suppose that $ a_n≥0$ is a sequence of numbers. Explain why the sequence of partial sums of $ a_n$ is increasing.

Answer: $ S_{N+1}=a_{N+1}+S_N≥S_N$

64) [T] Suppose that $ a_n$ is a sequence of positive numbers and the sequence $ S_n$ of partial sums of $ a_n$ is bounded above. Explain why $\displaystyle \sum_{n=1}^∞a_n$ converges. Does the conclusion remain true if we remove the hypothesis $ a_n≥0$?

65) [T] Suppose that $ a_1=S_1=1$ and that, for given numbers $ S>1$ and $ 0<k<1$, one defines $ a_{n+1}=k(S−S_n)$ and $ S_{n+1}=a_{n+1}+S_n$. Does $ S_n$ converge? If so, to what? (Hint: First argue that $ S_n<S$ for all $ n$ and $ S_n$ is increasing.)

Answer: Since $ S>1, a_2>0,$ and since $ k<1, S_2=1+a_2<1+(S−1)=S$. If $ S_n>S$ for some $ n$, then there is a smallest $ n$. For this $ n, S>S_{n−1}$, so $ S_n=S_{n−1}+k(S−S_{n−1})=kS+(1−k)S_{n−1}<S$, a contradiction. Thus $ S_n<S$ and $ a_{n+1}>0$ for all $ n$, so $ S_n$ is increasing and bounded by $ S$. Let $\displaystyle S_∗=\lim S_n$. If $ S_∗<S$, then $ δ=k(S−S_∗)>0$, but we can find n such that $ S_∗−S_n<δ/2$, which implies that $ S_{n+1}=S_n+k(S−S_n) >S_∗+δ/2$, contradicting that Sn is increasing to $ S_∗$. Thus $ S_n→S.$

66) [T] A version of von Bertalanffy growth can be used to estimate the age of an individual in a homogeneous species from its length if the annual increase in year $ n+1$ satisfies $ a_{n+1}=k(S−S_n)$, with $ S_n$ as the length at year $ n, S$ as a limiting length, and $ k$ as a relative growth constant. If $ S_1=3, S=9,$ and $ k=1/2,$ numerically estimate the smallest value of n such that $ S_n≥8$. Note that $ S_{n+1}=S_n+a_{n+1}.$ Find the corresponding $ n$ when $ k=1/4.$

67) [T] Suppose that $\displaystyle \sum_{n=1}^∞a_n$ is a convergent series of positive terms. Explain why $\displaystyle \lim_{N→∞}\sum_{n=N+1}^∞a_n=0.$

Answer: Let $\displaystyle S_k=\sum_{n=1}^ka_n$ and $ S_k→L$. Then $ S_k$ eventually becomes arbitrarily close to $ L$, which means that $\displaystyle L−S_N=\sum_{n=N+1}^∞a_n$ becomes arbitrarily small as $ N→∞.$

68) [T] Find the length of the dashed zig-zag path in the following figure.

$alt$

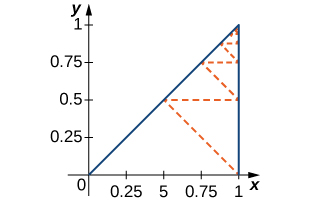
69) [T] Find the total length of the dashed path in the following figure.

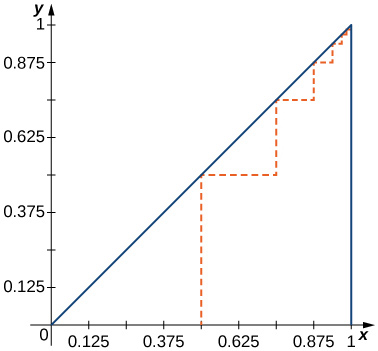
$This is a triangle drawn in quadrant 1 with vertices at (1, 1), (0, 0), and (1, 0). The zigzag line is drawn starting at (0.5, 0) and goes to the middle of the hypotenuse, the midpoint between that point and the vertical leg, the midpoint of the upper half of the hypotenuse, the midpoint between that point and the vertical leg, and so on until it converges on the top vertex.$

Answer: $\displaystyle L=\left(1+\frac{1}{2}\right)\sum_{n=1}^∞\frac{1}{2^n}=\frac{3}{2}$.

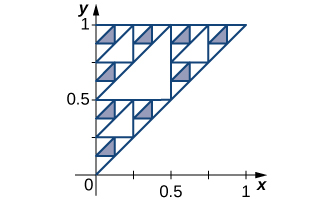
70) [T] The Sierpinski triangle is obtained from a triangle by deleting the middle fourth as indicated in the first step, by deleting the middle fourths of the remaining three congruent triangles in the second step, and in general deleting the middle fourths of the remaining triangles in each successive step. Assuming that the original triangle is shown in the figure, find the areas of the remaining parts of the original triangle after $ N$ steps and find the total length of all of the boundary triangles after $ N$ steps.

$alt$

71) [T] The Sierpinski gasket is obtained by dividing the unit square into nine equal sub-squares, removing the middle square, then doing the same at each stage to the remaining sub-squares. The figure shows the remaining set after four iterations. Compute the total area removed after $ N$ stages, and compute the length the total perimeter of the remaining set after $ N$ stages.

$This is a black square with many smaller squares removed from it, leaving behind blank spaces in a pattern of squares. There are four iterations of the removal process. At the first, the central 1/9 square area is removed. Each side is 1/3 of that of the next larger square. Next, eight smaller squares are removed around this one. Eight smaller squares are removed from around each of those – 64 in total. Eight even smaller ones are removed from around each of those 64.$

Answer: At stage one a square of area $ 1/9$ is removed, at stage $ 2$ one removes $ 8$ squares of area $ 1/9^2$, at stage three one removes $ 8^2$ squares of area $ 1/9^3$, and so on. The total removed area after $ N$ stages is $\displaystyle \sum_{n=0}^{N−1}\frac{8^N}{9^{N+1}}=\frac{1}{8}\cdot\frac{1−(8/9)^N}{1−8/9}→1$ as $N→∞.$ The total perimeter is $\displaystyle 4+4\sum_{n=0}^∞\frac{8^N}{3^{N+1}}→∞.$

9.3: The Divergence and Integral Tests

For each sequence in exercises 1 - 14, if the divergence test applies, either state that $\displaystyle \lim_{n→∞}a_n$ does not exist or find $\displaystyle \lim_{n→∞}a_n$. If the divergence test does not apply, state why.

1) $ a_n=\dfrac{n}{n+2}$

2) $ a_n=\dfrac{n}{5n^2−3}$

Answer: $\displaystyle \lim_{n→∞}a_n=0$. The Divergence Test does not apply.

3) $ a_n=\dfrac{n}{\sqrt{3n^2+2n+1}}$

4) $ a_n=\dfrac{(2n+1)(n−1)}{(n+1)^2}$

Answer: $\displaystyle \lim_{n→∞}a_n=2$. So the series diverges by the $n^{\text{th}}$-Term Test for Divergence.

5) $ a_n=\dfrac{(2n+1)^{2n}}{(3n^2+1)^n}$

6) $ a_n=\dfrac{2^n}{3^{n/2}}$

Answer: $\displaystyle \lim_{n→∞}a_n=∞$ (does not exist). So the series diverges by the $n^{\text{th}}$-Term Test for Divergence.

7) $ a_n=\dfrac{2^n+3^n}{10^{n/2}}$

8) $ a_n=e^{−2/n}$

Answer: $\displaystyle \lim_{n→∞}a_n=1.$ So the series diverges by the $n^{\text{th}}$-Term Test for Divergence.

9) $ a_n=\cos n$

10) $ a_n=\tan n$

Answer: $\displaystyle \lim_{n→∞}a_n$ does not exist. So the series diverges by the $n^{\text{th}}$-Term Test for Divergence.

11) $ a_n=\dfrac{1−\cos^2(1/n)}{\sin^2(2/n)}$

12) $ a_n=\left(1−\dfrac{1}{n}\right)^{2n}$

Answer: $\displaystyle \lim_{n→∞}a_n=1/e^2.$ So the series diverges by the $n^{\text{th}}$-Term Test for Divergence.

13) $ a_n=\dfrac{\ln n}{n}$

14) $ a_n=\dfrac{(\ln n)^2}{\sqrt{n}}$

Answer: $\displaystyle \lim_{n→∞}a_n=0.$ The Divergence Test does not apply.

In exercises 15 - 20, state whether the given $ p$-series converges.

15) $\displaystyle \sum_{n=1}^∞\frac{1}{\sqrt{n}}$

16) $\displaystyle \sum_{n=1}^∞\frac{1}{n\sqrt{n}}$

Answer: The series converges, since $ p=3/2>1$.

17) $\displaystyle \sum_{n=1}^∞\frac{1}{\sqrt[3]{n^2}}$

18) $\displaystyle \sum_{n=1}^∞\frac{1}{\sqrt[3]{n^4}}$

Answer: The series converges, since $ p=4/3>1.$

19) $\displaystyle \sum_{n=1}^∞\frac{n^e}{n^π}$

20) $\displaystyle \sum_{n=1}^∞\frac{n^π}{n^{2e}}$

Answer: The series converges, since $ p=2e−π>1.$

In exercises 21 - 27, use the integral test to determine whether the following sums converge.

21) $\displaystyle \sum_{n=1}^∞\frac{1}{\sqrt{n+5}}$

22) $\displaystyle \sum_{n=1}^∞\frac{1}{\sqrt[3]{n+5}}$

Answer: The series diverges by the Integral Test since $\displaystyle ∫^∞_1\frac{dx}{(x+5)^{1/3}}$ can be shown to diverge.

23) $\displaystyle \sum_{n=2}^∞\frac{1}{n\ln n}$

24) $\displaystyle \sum_{n=1}^∞\frac{n}{1+n^2}$

Answer: The series diverges by the Integral Test since $\displaystyle ∫^∞_1\frac{x}{1+x^2}\,dx$ can be shown to diverge.

25) $\displaystyle \sum_{n=1}^∞\frac{e^n}{1+e^{2n}}$

26) $\displaystyle \sum_{n=1}^∞\frac{2n}{1+n^4}$

Answer: The series converges by the Integral Test since $\displaystyle ∫^∞_1\frac{2x}{1+x^4}\,dx$ converges.

27) $\displaystyle \sum_{n=2}^∞\frac{1}{n\ln^2n}$

Express the sums in exercises 28 - 31 as $ p$-series and determine whether each converges.

28) $\displaystyle \sum_{n=1}^∞2^{−\ln n}$ (Hint: $ 2^{−\ln n}=1/n^{\ln 2}.)$

Answer: $ 2^{−\ln n}=1/n^{\ln 2}.$ Since $p=\ln 2<1$, this series diverges by the $ p$-series test.

29) $\displaystyle \sum_{n=1}^∞3^{−\ln n}$ (Hint: $ 3^{−\ln n}=1/n^{\ln 3}.)$

30) $\displaystyle \sum_{n=1}^n2^{−2\ln n}$

Answer: $ 2^{−2\ln n}=1/n^{2\ln 2}.$ Since $p = 2\ln 2−1<1$, this series diverges by the $ p$-series test.

31) $\displaystyle \sum_{n=1}^∞n3^{−2\ln n}$

In exercises 32 - 35, use the estimate $\displaystyle R_N≤∫^∞_Nf(t)\,dt$ to find a bound for the remainder $\displaystyle R_N=\sum_{n=1}^∞a_n−\sum_{n=1}^Na_n$ where $ a_n=f(n).$

32) $\displaystyle \sum_{n=1}^{1000}\frac{1}{n^2}$

Answer: $\displaystyle R_{1000}≤∫^∞_{1000}\frac{dt}{t^2}=\lim_{b\to ∞}−\frac{1}{t}\bigg|^b_{1000}=\lim_{b\to ∞}\left(−\frac{1}{b}+\frac{1}{1000}\right)=0.001$

33) $\displaystyle \sum_{n=1}^{1000}\frac{1}{n^3}$

34) $\displaystyle \sum_{n=1}^{1000}\frac{1}{1+n^2}$

Answer: $\displaystyle R_{1000}≤∫^∞_{1000}\frac{dt}{1+t^2}=\lim_{b\to ∞} \left(\tan^{−1}b−\tan^{−1}(1000)\right)=π/2−\tan^{−1}(1000)≈0.000999$

35) $\displaystyle \sum_{n=1}^{100}\frac{n}{2^n}$

[T] In exercises 36 - 40, find the minimum value of $ N$ such that the remainder estimate $\displaystyle ∫^∞_{N+1}f(x)\,dx<R_N<∫^∞_N f(x)\,dx$ guarantees that $\displaystyle \sum_{n=1}^Na_n$ estimates $\displaystyle \sum_{n=1}^∞a_n,$ accurate to within the given error.

36) $ a_n=\dfrac{1}{n^2},$ error $ <10^{−4}$

Answer: $\displaystyle R_N<∫^∞_N\frac{dx}{x^2}=1/N,\;\text{for}\;N>10^4$

37) $ a_n=\dfrac{1}{n^{1.1}},$ error $ <10^{−4}$

38) $ a_n=\dfrac{1}{n^{1.01}},$ error $ <10^{−4}$

Answer: $\displaystyle R_N<∫^∞_N\frac{dx}{x^{1.01}}=100N^{−0.01},\;\text{for}\;N>10^{600}$

39) $ a_n=\dfrac{1}{n\ln^2n},$ error $ <10^{−3}$

40) $ a_n=\dfrac{1}{1+n^2},$ error $ <10^{−3}$

Answer: $\displaystyle R_N<∫^∞_N\frac{dx}{1+x^2}=π/2−\tan^{−1}(N),\;\text{for}\;N>\tan(π/2−10^{−3})≈1000$

In exercises 41 - 45, find a value of $ N$ such that $ R_N$ is smaller than the desired error. Compute the corresponding sum $\displaystyle \sum_{n=1}^Na_n$ and compare it to the given estimate of the infinite series.

41) $ a_n=\dfrac{1}{n^{11}},$ error $ \displaystyle <10^{−4}, \sum_{n=1}^∞\frac{1}{n^{11}}=1.000494…$

42) $ a_n=\dfrac{1}{e^n},$ error $\displaystyle <10^{−5}, \sum_{n=1}^∞\frac{1}{e^n}=\frac{1}{e−1}=0.581976…$

Answer: $\displaystyle R_N<∫^∞_N\frac{dx}{e^x}=e^{−N},\;\text{for}\;N>5\ln(10),$ okay if $\displaystyle N=12;\sum_{n=1}^{12}e^{−n}=0.581973....$ Estimate agrees with $ 1/(e−1)$ to five decimal places.

43) $ a_n=\dfrac{1}{e^{n^2}},$ error $\displaystyle <10^{−5}, \sum_{n=1}^∞\dfrac{1}{e^{n^2}}=0.40488139857…$

44) $ a_n=\dfrac{1}{n^4},$ error $\displaystyle <10^{−4}, \sum_{n=1}^∞\dfrac{1}{n^4}=\frac{π^4}{90}=1.08232...$

Answer: $\displaystyle R_N<∫^∞_N\dfrac{dx}{x^4}=4/N^3,\;\text{for}\;N>(4.10^4)^{1/3},$ okay if $ N=35$; $\displaystyle \sum_{n=1}^{35}\dfrac{1}{n^4}=1.08231….$ Estimate agrees with the sum to four decimal places.

45) $ a_n=\dfrac{1}{n^6}$, error $\displaystyle <10^{−6}, \sum_{n=1}^∞\frac{1}{n^6}=\frac{π^6}{945}=1.01734306...,$

46) Find the limit as $ n→∞$ of $ \dfrac{1}{n}+\dfrac{1}{n+1}+⋯+\dfrac{1}{2n}$. (Hint: Compare to $\displaystyle ∫^{2n}_n\frac{1}{t}\,dt.$)

Answer: $ \ln(2)$

47) Find the limit as $ n→∞$ of $ \dfrac{1}{n}+\dfrac{1}{n+1}+⋯+\dfrac{1}{3n}$

The next few exercises are intended to give a sense of applications in which partial sums of the harmonic series arise.

48) In certain applications of probability, such as the so-called Watterson estimator for predicting mutation rates in population genetics, it is important to have an accurate estimate of the number $ H_k=(1+\frac{1}{2}+\frac{1}{3}+⋯+\frac{1}{k})$. Recall that $ T_k=H_k−\ln k$ is decreasing. Compute $\displaystyle T=\lim_{k→∞}T_k$ to four decimal places. (Hint: $\displaystyle \frac{1}{k+1}<∫^{k+1}_k\frac{1}{x}\,dx$.)

Answer: $ T=0.5772...$

49) [T] Complete sampling with replacement, sometimes called the coupon collector’s problem, is phrased as follows: Suppose you have $ N$ unique items in a bin. At each step, an item is chosen at random, identified, and put back in the bin. The problem asks what is the expected number of steps $ E(N)$ that it takes to draw each unique item at least once. It turns out that $ E(N)=N.H_N=N(1+\frac{1}{2}+\frac{1}{3}+⋯+\frac{1}{N})$. Find $ E(N)$ for $ N=10,20,$ and $ 50$.

50) [T] The simplest way to shuffle cards is to take the top card and insert it at a random place in the deck, called top random insertion, and then repeat. We will consider a deck to be randomly shuffled once enough top random insertions have been made that the card originally at the bottom has reached the top and then been randomly inserted. If the deck has $ n$ cards, then the probability that the insertion will be below the card initially at the bottom (call this card $ B$) is $ 1/n$. Thus the expected number of top random insertions before $ B$ is no longer at the bottom is $ n$. Once one card is below $ B$, there are two places below $ B$ and the probability that a randomly inserted card will fall below $ B$ is $ 2/n$. The expected number of top random insertions before this happens is $ n/2$. The two cards below $ B$ are now in random order. Continuing this way, find a formula for the expected number of top random insertions needed to consider the deck to be randomly shuffled.

Answer: The expected number of random insertions to get $ B$ to the top is $ n+n/2+n/3+⋯+n/(n−1).$ Then one more insertion puts $ B$ back in at random. Thus, the expected number of shuffles to randomize the deck is $ n(1+1/2+⋯+1/n).$

51) Suppose a scooter can travel $ 100$ km on a full tank of fuel. Assuming that fuel can be transferred from one scooter to another but can only be carried in the tank, present a procedure that will enable one of the scooters to travel $ 100H_N$ km, where $ H_N=1+1/2+⋯+1/N.$

52) Show that for the remainder estimate to apply on $ [N,∞)$ it is sufficient that $ f(x)$ be decreasing on $ [N,∞)$, but $ f$ need not be decreasing on $ [1,∞).$

Answer: Set $ b_n=a_{n+N}$ and $ g(t)=f(t+N)$ such that $ f$ is decreasing on $ [t,∞).$

53) [T] Use the remainder estimate and integration by parts to approximate $\displaystyle \sum_{n=1}^∞\frac{n}{e^n}$ within an error smaller than $ 0.0001.$

54) Does $\displaystyle \sum_{n=2}^∞\frac{1}{n(\ln n)^p}$ converge if $ p$ is large enough? If so, for which $ p$?

Answer: The series converges for $ p>1$ by integral test using change of variable.

55) [T] Suppose a computer can sum one million terms per second of the divergent series $\displaystyle \sum_{n=1}^N\frac{1}{n}$. Use the integral test to approximate how many seconds it will take to add up enough terms for the partial sum to exceed $ 100$.

56) [T] A fast computer can sum one million terms per second of the divergent series $\displaystyle \sum_{n=2}^N\frac{1}{n\ln n}$. Use the integral test to approximate how many seconds it will take to add up enough terms for the partial sum to exceed $ 100.$

Answer: $ N=e^{e^{100}}≈e^{10^{43}}$ terms are needed.

9.4: Comparison Tests

Use the Comparison Test to determine whether each series in exercises 1 - 13 converges or diverges.

1) $\displaystyle \sum^∞_{n=1}a_n$ where $a_n=\dfrac{2}{n(n+1)}$

2) $\displaystyle \sum^∞_{n=1}a_n$ where $a_n=\dfrac{1}{n(n+1/2)}$

Answer: Converges by comparison with $\dfrac{1}{n^2}$.

3) $\displaystyle \sum^∞_{n=1}\frac{1}{2(n+1)}$

4) $\displaystyle \sum^∞_{n=1}\frac{1}{2n−1}$

Answer: Diverges by comparison with harmonic series, since $2n−1≥n.$

5) $\displaystyle \sum^∞_{n=2}\frac{1}{(n\ln n)^2}$

6) $\displaystyle \sum^∞_{n=1}\frac{n!}{(n+2)!}$

Answer: $a_n=1/(n+1)(n+2)<1/n^2.$ Converges by comparison with $p$-series, $p=2>1$.

7) $\displaystyle \sum^∞_{n=1}\frac{1}{n!}$

8) $\displaystyle \sum^∞_{n=1}\frac{\sin(1/n)}{n}$

Answer: $\sin(1/n)≤1/n,$ so converges by comparison with $p$-series, $p=2>1$.

9) $\displaystyle \sum_{n=1}^∞\frac{\sin^2n}{n^2}$

10) $\displaystyle \sum_{n=1}^∞\frac{\sin(1/n)}{\sqrt{n}}$

Answer: $\sin(1/n)≤1,$ so converges by comparison with $p$-series, $p=3/2>1.$

11) $\displaystyle \sum^∞_{n=1}\frac{n^{1.2}−1}{n^{2.3}+1}$

12) $\displaystyle \sum^∞_{n=1}\frac{\sqrt{n+1}−\sqrt{n}}{n}$

Answer: Since $\sqrt{n+1}−\sqrt{n}=1/(\sqrt{n+1}+\sqrt{n})≤2/\sqrt{n},$ series converges by comparison with $p$-series for $p=1.5>1$.

13) $\displaystyle \sum^∞_{n=1}\frac{\sqrt[4]{n}}{\sqrt[3]{n^4+n^2}}$

Use the Limit Comparison Test to determine whether each series in exercises 14 - 28 converges or diverges.

14) $\displaystyle \sum^∞_{n=1}\left(\frac{\ln n}{n}\right)^2$

Answer: Converges by limit comparison with $p$-series for $p>1$.

15) $\displaystyle \sum^∞_{n=1}\left(\frac{\ln n}{n^{0.6}}\right)^2$

16) $\displaystyle \sum^∞_{n=1}\frac{\ln\left(1+\frac{1}{n}\right)}{n}$

Answer: Converges by limit comparison with $p$-series, $p=2>1.$

17) $\displaystyle \sum^∞_{n=1}\ln\left(1+\frac{1}{n^2}\right)$

18) $\displaystyle \sum^∞_{n=1}\frac{1}{4^n−3^n}$

Answer: Converges by limit comparison with $4^{−n}$.

19) $\displaystyle \sum^∞_{n=1}\frac{1}{n^2−n\sin n}$

20) $\displaystyle \sum^∞_{n=1}\frac{1}{e^{(1.1)n}−3^n}$

Answer: Converges by limit comparison with $1/e^{1.1n}$.

21) $\displaystyle \sum^∞_{n=1}\frac{1}{e^{(1.01)n}−3^n}$

22) $\displaystyle \sum^∞_{n=1}\frac{1}{n^{1+1/n}}$

Answer: Diverges by limit comparison with harmonic series.

23) $\displaystyle \sum^∞_{n=1}\frac{1}{2^{1+1/n}}{n^{1+1/n}}$

24) $\displaystyle \sum^∞_{n=1}\left(\frac{1}{n}−\sin\left(\frac{1}{n}\right)\right)$

Answer: Converges by limit comparison with $p$-series, $p=3>1$.

25) $\displaystyle \sum^∞_{n=1}\left(1−\cos\left(\frac{1}{n}\right)\right)$

26) $\displaystyle \sum^∞_{n=1}\frac{1}{n}\left(\tan^{−1}n−\frac{π}{2}\right)$

Answer: Converges by limit comparison with $p$-series, $p=3>1$.

27) $\displaystyle \sum^∞_{n=1}\left(1−\frac{1}{n}\right)^{n.n}$ (Hint:$\left(1−\dfrac{1}{n}\right)^n→1/e.$)

28) $\displaystyle \sum^∞_{n=1}\left(1−e^{−1/n}\right)$ (Hint:$1/e≈(1−1/n)^n,$ so $1−e^{−1/n}≈1/n.$)

Answer: Diverges by limit comparison with $1/n$.

29) Does $\displaystyle \sum^∞_{n=2}\frac{1}{(\ln n)^p}$ converge if $p$ is large enough? If so, for which $p?$

30) Does $\displaystyle \sum^∞_{n=1}\left(\frac{(\ln n)}{n}\right)^p$ converge if $p$ is large enough? If so, for which $p?$

Answer: Converges for $p>1$ by comparison with a $p$ series for slightly smaller $p$.

31) For which $p$ does the series $\displaystyle \sum^∞_{n=1}2^{pn}/3^n$ converge?

32) For which $p>0$ does the series $\displaystyle \sum^∞_{n=1}\frac{n^p}{2^n}$ converge?

Answer: Converges for all $p>0$.

33) For which $r>0$ does the series $\displaystyle \sum^∞_{n=1}\frac{r^{n^2}}{2^n}$ converge?

34) For which $r>0$ does the series $\displaystyle \sum^∞_{n=1}\frac{2^n}{r^{n^2}}$ converge?

Answer: Converges for all $r>1$. If $r>1$ then $r^n>4$, say, once $n>\ln(2)/\ln(r)$ and then the series converges by limit comparison with a geometric series with ratio $1/2$.

35) Find all values of $p$ and $q$ such that $\displaystyle \sum^∞_{n=1}\frac{n^p}{(n!)^q}$ converges.

36) Does $\displaystyle \sum^∞_{n=1}\frac{\sin^2(nr/2)}{n}$ converge or diverge? Explain.

Answer: The numerator is equal to $1$ when $n$ is odd and $0$ when $n$ is even, so the series can be rewritten $\displaystyle \sum^∞_{n=1}\frac{1}{2n+1},$ which diverges by limit comparison with the harmonic series.

37) Explain why, for each $n$, at least one of ${|\sin n|,|\sin(n+1)|,...,|\sin(n+6)|}$ is larger than $1/2$. Use this relation to test convergence of $\displaystyle \sum^∞_{n=1}\frac{|\sin n|}{\sqrt{n}}$.

38) Suppose that $a_n≥0$ and $b_n≥0$ and that $\displaystyle \sum_{n=1}^∞a^2_n$ and $\displaystyle \sum_{n=1}^∞b^2_n$ converge. Prove that $\displaystyle \sum_{n=1}^∞a_nb_n$ converges and $\displaystyle \sum_{n=1}^∞a_nb_n≤\frac{1}{2}\left(\sum_{n=1}^∞a^2_n+\sum_{n=1}^∞b^2_n\right)$.

Answer: $(a−b)^2=a^2−2ab+b^2$ or $a^2+b^2≥2ab$, so convergence follows from comparison of $2a_nb_n$ with $a^2_n+b^2_n.$ Since the partial sums on the left are bounded by those on the right, the inequality holds for the infinite series.

39) Does $\displaystyle \sum_{n=1}^∞2^{−\ln\ln n}$ converge? (Hint: Write $2^{\ln\ln n}$ as a power of $\ln n$.)

40) Does $\displaystyle \sum_{n=1}^∞(\ln n)^{−\ln n}$ converge? (Hint: Use $t=e^{\ln(t)}$ to compare to a $p$−series.)

Answer: $(\ln n)^{−\ln n}=e^{−\ln(n)\ln\ln(n)}.$ If $n$ is sufficiently large, then $\ln\ln n>2,$ so $(\ln n)^{−\ln n}<1/n^2$, and the series converges by comparison to a $p$−series.

41) Does $\displaystyle \sum_{n=2}^∞(\ln n)^{−\ln\ln n}$ converge? (Hint: Compare $a_n$ to $1/n$.)

42) Show that if $a_n≥0$ and $\displaystyle \sum_{n=1}^∞a_n$ converges, then $\displaystyle \sum_{n=1}^∞a^2_n$ converges. If $\displaystyle \sum_{n=1}^∞a^2_n$ converges, does $\displaystyle \sum_{n=1}^∞a_n$ necessarily converge?

Answer: $a_n→0,$ so $a^2_n≤|a_n|$ for large $n$. Convergence follows from limit comparison. $\displaystyle \sum_{n=1}^∞\frac{1}{n^2}$ converges, but $\displaystyle \sum_{n=1}^∞\frac{1}{n}$ does not, so the fact that $\displaystyle \sum_{n=1}^∞a^2_n$ converges does not imply that $\displaystyle \sum_{n=1}^∞a_n$ converges.

43) Suppose that $a_n>0$ for all $n$ and that $\displaystyle \sum_{n=1}^∞a_n$ converges. Suppose that $b_n$ is an arbitrary sequence of zeros and ones. Does $\displaystyle \sum_{n=1}^∞a_nb_n$ necessarily converge?

44) Suppose that $a_n>0$ for all $n$ and that $\displaystyle \sum_{n=1}^∞a_n$ diverges. Suppose that $b_n$ is an arbitrary sequence of zeros and ones with infinitely many terms equal to one. Does $\displaystyle \sum_{n=1}^∞a_nb_n$ necessarily diverge?

Answer: No. $\displaystyle \sum_{n=1}^∞1/n$ diverges. Let $b_k=0$ unless $k=n^2$ for some $n$. Then $\displaystyle \sum_kb_k/k=\sum1/k^2$ converges.

45) Complete the details of the following argument: If $\displaystyle \sum_{n=1}^∞\frac{1}{n}$ converges to a finite sum $s$, then $\dfrac{1}{2}s=\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{6}+⋯$ and $s−\dfrac{1}{2}s=1+\dfrac{1}{3}+\dfrac{1}{5}+⋯.$ Why does this lead to a contradiction?

46) Show that if $a_n≥0$ and $\displaystyle \sum_{n=1}^∞a^2_n$ converges, then $\displaystyle \sum_{n=1}^∞\sin^2(a_n)$ converges.

Answer: $|\sin t|≤|t|,$ so the result follows from the comparison test.

47) Suppose that $a_n/b_n→0$ in the comparison test, where $a_n≥0$ and $b_n≥0$. Prove that if $\displaystyle \sum b_n$ converges, then $\displaystyle \sum a_n$ converges.

48) Let $b_n$ be an infinite sequence of zeros and ones. What is the largest possible value of $\displaystyle x=\sum_{n=1}^∞b_n/2^n$?

Answer: By the comparison test, $\displaystyle x=\sum_{n=1}^∞b_n/2^n≤\sum_{n=1}^∞1/2^n=1.$

49) Let $d_n$ be an infinite sequence of digits, meaning $d_n$ takes values in $\{0,1,…,9\}$. What is the largest possible value of $\displaystyle x=\sum_{n=1}^∞d_n/10^n$ that converges?

50) Explain why, if $x>1/2,$ then $x$ cannot be written $\displaystyle x=\sum_{n=2}^∞\frac{b_n}{2^n}\quad (b_n=0\;\text{or}\;1,\;b_1=0).$

Answer: If $b_1=0,$ then, by comparison, $\displaystyle x≤\sum_{n=2}^∞1/2^n=1/2.$

51) [T] Evelyn has a perfect balancing scale, an unlimited number of $1$-kg weights, and one each of $1/2$-kg, $1/4$-kg, $1/8$-kg, and so on weights. She wishes to weigh a meteorite of unspecified origin to arbitrary precision. Assuming the scale is big enough, can she do it? What does this have to do with infinite series?

52) [T] Robert wants to know his body mass to arbitrary precision. He has a big balancing scale that works perfectly, an unlimited collection of $1$-kg weights, and nine each of $0.1$-kg, $0.01$-kg, $0.001$-kg, and so on weights. Assuming the scale is big enough, can he do this? What does this have to do with infinite series?

Answer: Yes. Keep adding $1$-kg weights until the balance tips to the side with the weights. If it balances perfectly, with Robert standing on the other side, stop. Otherwise, remove one of the $1$-kg weights, and add $0.1$-kg weights one at a time. If it balances after adding some of these, stop. Otherwise if it tips to the weights, remove the last \$0.1$-kg weight. Start adding $0.01$-kg weights. If it balances, stop. If it tips to the side with the weights, remove the last $0.01$-kg weight that was added. Continue in this way for the $0.001$-kg weights, and so on. After a finite number of steps, one has a finite series of the form $\displaystyle A+\sum_{n=1}^Ns_n/10^n$ where $A$ is the number of full kg weights and $d_n$ is the number of $1/10^n$-kg weights that were added. If at some state this series is Robert’s exact weight, the process will stop. Otherwise it represents the $N^{\text{th}}$ partial sum of an infinite series that gives Robert’s exact weight, and the error of this sum is at most $1/10^N$.

53) The series $\displaystyle \sum_{n=1}^∞\frac{1}{2n}$ is half the harmonic series and hence diverges. It is obtained from the harmonic series by deleting all terms in which $n$ is odd. Let $m>1$ be fixed. Show, more generally, that deleting all terms $1/n$ where $n=mk$ for some integer $k$ also results in a divergent series.

54) In view of the previous exercise, it may be surprising that a subseries of the harmonic series in which about one in every five terms is deleted might converge. A depleted harmonic series is a series obtained from $\displaystyle \sum_{n=1}^∞\frac{1}{n}$ by removing any term $1/n$ if a given digit, say $9$, appears in the decimal expansion of $n$. Argue that this depleted harmonic series converges by answering the following questions.

a. How many whole numbers $n$ have $d$ digits?

b. How many $d$-digit whole numbers $h(d)$. do not contain $9$ as one or more of their digits?

c. What is the smallest $d$-digit number $m(d)$?

d. Explain why the deleted harmonic series is bounded by $\displaystyle \sum_{d=1}^∞\frac{h(d)}{m(d)}$.

e. Show that $\displaystyle \sum_{d=1}^∞\frac{h(d)}{m(d)}$ converges.

Answer: a. $10^d−10^{d−1}<10^d$
b. $h(d)<9^d$
c. $m(d)=10^{d−1}+1$
d. Group the terms in the deleted harmonic series together by number of digits. $h(d)$ bounds the number of terms, and each term is at most $\frac{1}{m(d)}.$
Then $\displaystyle \sum_{d=1}^∞h(d)/m(d)≤\sum_{d=1}^∞9^d/(10)^{d−1}≤90$. One can actually use comparison to estimate the value to smaller than $80$. The actual value is smaller than $23$.

55) Suppose that a sequence of numbers $a_n>0$ has the property that $a_1=1$ and $a_{n+1}=\dfrac{1}{n+1}S_n$, where $S_n=a_1+⋯+a_n$. Can you determine whether $\displaystyle \sum_{n=1}^∞a_n$ converges? (Hint: $S_n$ is monotone.)

56) Suppose that a sequence of numbers $a_n>0$ has the property that $a_1=1$ and $a_{n+1}=\dfrac{1}{(n+1)^2}S_n$, where $S_n=a_1+⋯+a_n$. Can you determine whether $\displaystyle \sum_{n=1}^∞a_n$ converges? (Hint: $S_2=a_2+a_1=a_2+S_1=a_2+1=1+1/4=(1+1/4)S_1, S_3=\dfrac{1}{3^2}S_2+S_2=(1+1/9)S_2=(1+1/9)(1+1/4)S_1$, etc. Look at $\ln(S_n)$, and use $\ln(1+t)≤t, t>0.$)

Answer: Continuing the hint gives $S_N=(1+1/N^2)(1+1/(N−1)^2…(1+1/4)).$ Then $\ln(S_N)=\ln(1+1/N^2)+\ln(1+1/(N−1)^2)+⋯+\ln(1+1/4).$ Since $\ln(1+t)$ is bounded by a constant times $t$, when $0<t<1$ one has $\displaystyle \ln(S_N)≤C\sum_{n=1}^N\frac{1}{n^2}$, which converges by comparison to the $p$-series for $p=2$.

9.5: Alternating Series

In exercises 1 - 30, state whether each of the following series converges absolutely, conditionally, or not at all.

1) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n}{n+3}$

2) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{\sqrt{n}+1}{\sqrt{n}+3}$

Answer: This series diverges by the divergence test. Terms do not tend to zero.

3) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{1}{\sqrt{n+3}}$

4) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{\sqrt{n+3}}{n}$

Answer: Converges conditionally by alternating series test, since $\sqrt{n+3}/n$ is decreasing and its limit is 0. Does not converge absolutely by comparison with $p$-series, $p=1/2$.

5) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{1}{n!}$

6) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{3^n}{n!}$

Answer: Converges absolutely by limit comparison to $3^n/4^n,$ for example.

7) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\left(\frac{n−1}{n}\right)^n$

8) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\left(\frac{n+1}{n}\right)^n$

Answer: Diverges by divergence test since $\displaystyle \lim_{n→∞}|a_n|=e$ and not $0$.

9) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\sin^2n$

10) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\cos^2n$

Answer: Diverges by the divergence test, since its terms do not tend to zero. The limit of the sequence of its terms does not exist.

11) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\sin^2(1/n)$

12) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\cos^2(1/n)$

Answer: $\displaystyle \lim_{n→∞}\cos^2(1/n)=1.$ Diverges by divergence test.

13) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\ln(1/n)$

14) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\ln(1+\frac{1}{n})$

Answer: Converges by alternating series test.

15) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n^2}{1+n^4}$

16) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n^e}{1+n^π}$

Answer: Converges conditionally by alternating series test. Does not converge absolutely by limit comparison with $p$-series, $p=π−e$

Solution:

17) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}2^{1/n}$

18) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}n^{1/n}$

Answer: Diverges; terms do not tend to zero.

19) $\displaystyle \sum^∞_{n=1}(−1)^n(1−n^{1/n})$ (Hint: $n^{1/n}≈1+\ln(n)/n$ for large $n$.)

20) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}n\left(1−\cos\left(\frac{1}{n}\right)\right)$ (Hint: $\cos(1/n)≈1−1/n^2$ for large $n$.)

Answer: Converges by alternating series test. Does not converge absolutely by limit comparison with harmonic series.

21) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}(\sqrt{n+1}−\sqrt{n})$ (Hint: Rationalize the numerator.)

22) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\left(\frac{1}{\sqrt{n}}−\frac{1}{\sqrt{n+1}}\right)$ (Hint: Cross-multiply then rationalize numerator.)

Answer: Converges absolutely by limit comparison with $p$-series, $p=3/2$, after applying the hint.

23) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}(\ln(n+1)−\ln n)$

24) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}n(\tan^{−1}(n+1)−\tan^{−1}n)$ (Hint: Use Mean Value Theorem.)

Answer: Converges by alternating series test since $ n(\tan^{−1}(n+1)−\tan^{−1}n)$ is decreasing to zero for large $n$.Does not converge absolutely by limit comparison with harmonic series after applying hint.

25) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}((n+1)^2−n^2)$

26) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\left(\frac{1}{n}−\frac{1}{n+1}\right)$

Answer: Converges absolutely, since $ a_n=\dfrac{1}{n}−\dfrac{1}{n+1}$ are terms of a telescoping series.

27) $\displaystyle \sum^∞_{n=1}\frac{\cos(nπ)}{n}$

28) $\displaystyle \sum^∞_{n=1}\frac{\cos(nπ)}{n^{1/n}}$

Answer: Terms do not tend to zero. Series diverges by divergence test.

29) $\displaystyle \sum^∞_{n=1}\frac{1}{n}\sin(\frac{nπ}{2})$

30) $\displaystyle \sum^∞_{n=1}\sin(nπ/2)\sin(1/n)$

Answer: Converges by alternating series test. Does not converge absolutely by limit comparison with harmonic series.

In exercises 31 - 36, use the estimate $|R_N|≤b_{N+1}$ to find a value of $N$ that guarantees that the sum of the first $N$ terms of the alternating series $\displaystyle \sum^∞_{n=1}(−1)^{n+1}b_n$ differs from the infinite sum by at most the given error. Calculate the partial sum $S_N$ for this $N$.

31) [T] $b_n=1/n,$ error $ <10^{−5}$

32) [T] $b_n=1/\ln(n), n≥2,$ error $<10^{−1}$

Answer: $ \ln(N+1)>10, N+1>e^{10}, N≥22026; S_{22026}=0.0257…$

33) [T] $b_n=1/\sqrt{n},$ error $<10^{−3}$

34) [T] $b_n=1/2^n$, error $<10^{−6}$

Answer: $2^{N+1}>10^6$ or $N+1>6\ln(10)/\ln(2)=19.93.$ or $N≥19; S_{19}=0.333333969…$

35) [T] $b_n=ln(1+\dfrac{1}{n}),$ error $ <10^{−3}$

36) [T] $b_n=1/n^2,$ error $<10^{−6}$

Answer: $(N+1)^2>10^6$ or $N>999; S_{1000}≈0.822466.$

For exercises 37 - 45, indicate whether each of the following statements is true or false. If the statement is false, provide an example in which it is false.

37) If $ b_n≥0$ is decreasing and $\displaystyle \lim_{n→∞}b_n=0$, then $\displaystyle \sum_{n=1}^∞(b_{2n−1}−b_{2n})$ converges absolutely.

38) If $ b_n≥0$ is decreasing, then $\displaystyle \sum_{n=1}^∞(b_{2n−1}−b_{2n})$ converges absolutely.

Answer: True. $b_n$ need not tend to zero since if $\displaystyle c_n=b_n−\lim b_n$, then $c_{2n−1}−c_{2n}=b_{2n−1}−b_{2n}.$

39) If $ b_n≥0$ and $\displaystyle \lim_{n→∞}b_n=0$ then $\displaystyle \sum_{n=1}^∞(\frac{1}{2}(b_{3n−2}+b_{3n−1})−b_{3n})$ converges.

40) If $b_n≥0$ is decreasing and $\displaystyle \sum_{n=1}^∞(b_{3n−2}+b_{3n−1}−b_{3n})$ converges then $\displaystyle \sum_{n=1}^∞b_{3n−2}$ converges.

Answer: True. $b_{3n−1}−b_{3n}≥0,$ so convergence of $\displaystyle \sum b_{3n−2}$ follows from the comparison test.

41) If $b_n≥0$ is decreasing and $\displaystyle \sum_{n=1}^∞(−1)^{n−1}b_n$ converges conditionally but not absolutely, then $b_n$ does not tend to zero.

42) Let $a^+_n=a_n$ if $a_n≥0$ and $ a^−_n=−a_n$ if $a_n<0$. (Also, $ a^+_n=0$ if $a_n<0$ and $a^−_n=0$ if $a_n≥0$.) If $\displaystyle \sum_{n=1}^∞a_n$ converges conditionally but not absolutely, then neither $\displaystyle \sum_{n=1}^∞a^+_n$ nor $\displaystyle \sum_{n=1}^∞a^−_n$ converge.

Answer: True. If one converges, then so must the other, implying absolute convergence.

43) Suppose that $a_n$ is a sequence of positive real numbers and that $\displaystyle \sum_{n=1}^∞a_n$ converges.

44) Suppose that $b_n$ is an arbitrary sequence of ones and minus ones. Does $\displaystyle \sum_{n=1}^∞a_nb_n$ necessarily converge?

45) Suppose that $a_n$ is a sequence such that $\displaystyle \sum_{n=1}^∞a_nb_n$ converges for every possible sequence $b_n$ of zeros and ones. Does $\displaystyle \sum_{n=1}^∞a_n$ converge absolutely?

Answer: Yes. Take $b_n=1$ if $a_n≥0$ and $ b_n=0$ if $a_n<0$. Then $\displaystyle \sum_{n=1}^∞a_nb_n=\sum_{n:a_n≥0}a_n$ converges. Similarly, one can show $\displaystyle \sum_{n:a_n<0}a_n$ converges. Since both series converge, the series must converge absolutely.

In exercises 46 - 49, the series do not satisfy the hypotheses of the alternating series test as stated. In each case, state which hypothesis is not satisfied. State whether the series converges absolutely.

46) $\displaystyle \sum_{n=1}^∞(−1)^{n+1}\frac{\sin^2n}{n}$

47) $\displaystyle \sum_{n=1}^∞(−1)^{n+1}\frac{\cos^2n}{n}$

Answer: Not decreasing. Does not converge absolutely.

48) $\displaystyle 1+\frac{1}{2}−\frac{1}{3}−\frac{1}{4}+\frac{1}{5}+\frac{1}{6}−\frac{1}{7}−\frac{1}{8}+⋯$

49) $\displaystyle 1+\frac{1}{2}−\frac{1}{3}+\frac{1}{4}+\frac{1}{5}−\frac{1}{6}+\frac{1}{7}+\frac{1}{8}−\frac{1}{9}+⋯$

Answer: Not alternating. Can be expressed as $\displaystyle \sum_{n=1}^∞\left(\frac{1}{3n−2}+\frac{1}{3n−1}−\frac{1}{3n}\right),$ which diverges by comparison with $\displaystyle \sum_{n=1}^∞\frac{1}{3n−2}.$

50) Show that the alternating series $\displaystyle 1−\frac{1}{2}+\frac{1}{2}−\frac{1}{4}+\frac{1}{3}−\frac{1}{6}+\frac{1}{4}−\frac{1}{8}+⋯$ does not converge. What hypothesis of the alternating series test is not met?

51) Suppose that $\displaystyle \sum a_n$ converges absolutely. Show that the series consisting of the positive terms $a_n$ also converges.

Answer: Let $a^+_n=a_n$ if $a_n≥0$ and $a^+_n=0$ if $ a_n<0$. Then $a^+_n≤|a_n|$ for all $n$ so the sequence of partial sums of $ a^+_n$ is increasing and bounded above by the sequence of partial sums of $ |a_n|$, which converges; hence, $\displaystyle \sum_{n=1}^∞a^+_n$ converges.

52) Show that the alternating series $\displaystyle \frac{2}{3}−\frac{3}{5}+\frac{4}{7}−\frac{5}{9}+⋯$ does not converge. What hypothesis of the alternating series test is not met?

53) The formula $\displaystyle \cos θ=1−\frac{θ^2}{2!}+\frac{θ^4}{4!}−\frac{θ^6}{6!}+⋯$ will be derived in the next chapter. Use the remainder $|R_N|≤b_{N+1}$ to find a bound for the error in estimating $\cos θ$ by the fifth partial sum $1−θ^2/2!+θ^4/4!−θ^6/6!+θ^8/8!$ for $θ=1, θ=π/6,$ and $θ=π.$

Answer: For $N=5$ one has $∣R_N∣b_6=θ^{10}/10!$. When $θ=1, R_5≤1/10!≈2.75×10^{−7}$. When $θ=π/6,$ $R_5≤(π/6)^{10}/10!≈4.26×10^{−10}$. When $θ=π, R_5≤π^{10}/10!=0.0258.$

54) The formula $\sin θ=θ−\dfrac{θ^3}{3!}+\dfrac{θ^5}{5!}−\dfrac{θ^7}{7!}+⋯$ will be derived in the next chapter. Use the remainder $|R_N|≤b_{N+1}$ to find a bound for the error in estimating $\sin θ$ by the fifth partial sum $θ−θ^3/3!+θ^5/5!−θ^7/7!+θ^9/9!$ for $θ=1, θ=π/6,$ and $θ=π.$

55) How many terms in $\cos θ=1−\dfrac{θ^2}{2!}+\dfrac{θ^4}{4!}−\dfrac{θ^6}{6!}+⋯$ are needed to approximate $\cos 1$ accurate to an error of at most $ 0.00001$?

Answer: Let $ b_n=1/(2n−2)!.$ Then $R_N≤1/(2N)!<0.00001$ when $(2N)!>10^5$ or $N=5$ and $\displaystyle 1−\frac{1}{2!}+\frac{1}{4!}−\frac{1}{6!}+\frac{1}{8!}=0.540325…$, whereas $\cos 1=0.5403023…$

56) How many terms in $\sin θ=θ−\dfrac{θ^3}{3!}+\dfrac{θ^5}{5!}−\dfrac{θ^7}{7!}+⋯$ are needed to approximate $\sin 1$ accurate to an error of at most $0.00001?$

57) Sometimes the alternating series $\displaystyle \sum_{n=1}^∞(−1)^{n−1}b_n$ converges to a certain fraction of an absolutely convergent series $\displaystyle \sum_{n=1}^∞b_n$ at a faster rate. Given that $\displaystyle \sum_{n=1}^∞\frac{1}{n^2}=\frac{π^2}{6}$, find $\displaystyle S=1−\frac{1}{2^2}+\frac{1}{3^2}−\frac{1}{4^2}+⋯$. Which of the series $\displaystyle 6\sum_{n=1}^∞\frac{1}{n^2}$ and $\displaystyle S\sum_{n=1}^∞\frac{(−1)^{n−1}}{n^2}$ gives a better estimation of $π^2$ using $1000$ terms?

Answer: Let $\displaystyle T=\sum\frac{1}{n^2}.$ Then $T−S=\dfrac{1}{2}T$, so $S=T/2$. $\displaystyle \sqrt{6×\sum_{n=1}^{1000}1/n^2}=3.140638…; \sqrt{\frac{1}{2}×\sum_{n=1}^{1000}(−1)^{n−1}/n^2}=3.141591…; π=3.141592….$ The alternating series is more accurate for $1000$ terms.

The alternating series in exercises 58 & 59 converge to given multiples of $π$. Find the value of $N$ predicted by the remainder estimate such that the $N^{\text{th}}$ partial sum of the series accurately approximates the left-hand side to within the given error. Find the minimum $N$ for which the error bound holds, and give the desired approximate value in each case. Up to $15$ decimals places, $ π=3.141592653589793….$

58) [T] $\displaystyle \frac{π}{4}=\sum_{n=0}^∞\frac{(−1)^n}{2n+1},$ error $<0.0001$

59) [T] $\displaystyle \frac{π}{\sqrt{12}}=\sum_{k=0}^∞\frac{(−3)^{−k}}{2k+1},$ error $<0.0001$

Answer: $N=6, S_N=0.9068$

60) [T] The series $\displaystyle \sum_{n=0}^∞\frac{\sin(x+πn)}{x+πn}$ plays an important role in signal processing. Show that $\displaystyle \sum_{n=0}^∞\frac{\sin(x+πn)}{x+πn}$ converges whenever $0<x<π$. (Hint: Use the formula for the sine of a sum of angles.)

61) [T] If $\displaystyle \sum_{n=1}^N(−1)^{n−1}\frac{1}{n}→ln2,$ what is $\displaystyle 1+\frac{1}{3}+\frac{1}{5}−\frac{1}{2}−\frac{1}{4}−\frac{1}{6}+\frac{1}{7}+\frac{1}{9}+\frac{1}{11}−\frac{1}{8}−\frac{1}{10}−\frac{1}{12}+⋯?$

Answer: $\ln(2).$ The $n^{\text{th}}$ partial sum is the same as that for the alternating harmonic series.

62) [T] Plot the series $\displaystyle \sum_{n=1}^{100}\frac{\cos(2πnx)}{n}$ for $0≤x<1$. Explain why $\displaystyle \sum_{n=1}^{100}\frac{\cos(2πnx)}{n}$ diverges when $x=0,1$. How does the series behave for other $x$?

63) [T] Plot the series $\displaystyle \sum_{n=1}^{100}\frac{\sin(2πnx)}{n}$ for $0≤x<1$ and comment on its behavior

Answer

The series jumps rapidly near the endpoints. For $x$ away from the endpoints, the graph looks like $ π(1/2−x)$.

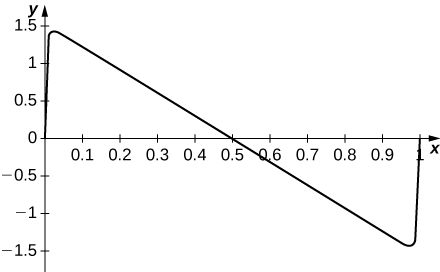
$This shows a function in quadrants 1 and 4 that begins at (0, 0), sharply increases to just below 1.5 close to the y axis, decreases linearly, crosses the x axis at 0.5, continues to decrease linearly, and sharply increases just before 1 to 0.$

64) [T] Plot the series $\displaystyle \sum_{n=1}^{100}\frac{\cos(2πnx)}{n^2}$ for $ 0≤x<1$ and describe its graph.

65) [T] The alternating harmonic series converges because of cancelation among its terms. Its sum is known because the cancelation can be described explicitly. A random harmonic series is one of the form $\displaystyle \sum_{n=1}^∞\frac{S_n}{n}$, where $s_n$ is a randomly generated sequence of $±1's$ in which the values $±1$ are equally likely to occur. Use a random number generator to produce $1000$ random $±1's$ and plot the partial sums $\displaystyle S_N=\sum_{n=1}^N\frac{s_n}{n}$ of your random harmonic sequence for $N=1$ to $1000$. Compare to a plot of the first $1000$ partial sums of the harmonic series.

Answer

Here is a typical result. The top curve consists of partial sums of the harmonic series. The bottom curve plots partial sums of a random harmonic series.

$This shows two curves. The top is an increasing concave down curve. The bottom is a jagged, random harmonic series plot that stays close to 0.$

66) [T] Estimates of $\displaystyle \sum_{n=1}^∞\frac{1}{n^2}$ can be accelerated by writing its partial sums as $\displaystyle \sum_{n=1}^N\frac{1}{n^2}=\sum_{n=1}^N\frac{1}{n(n+1)}+\sum_{n=1}^N\frac{1}{n^2(n+1)}$ and recalling that $\displaystyle \sum_{n=1}^N\frac{1}{n(n+1)}=1−\frac{1}{N+1}$ converges to one as $ N→∞.$ Compare the estimate of $π^2/6$ using the sums $\displaystyle \sum_{n=1}^{1000}\frac{1}{n^2}$ with the estimate using $\displaystyle 1+\sum_{n=1}^{1000}\frac{1}{n^2(n+1)}$.

67) [T] The Euler transform rewrites $\displaystyle S=\sum_{n=0}^∞(−1)^nb_n$ as $\displaystyle S=\sum_{n=0}^∞(−1)^n2^{−n−1}\sum_{m=0}^n(^n_m)b_{n−m}$. For the alternating harmonic series, it takes the form $\displaystyle \ln(2)=\sum_{n=1}^∞\frac{(−1)^{n−1}}{n}=\sum_{n=1}^∞\frac{1}{n2^n}$. Compute partial sums of $\displaystyle \sum_{n=1}^∞\frac{1}{n2^n}$ until they approximate $\ln(2)$ accurate to within $0.0001$. How many terms are needed? Compare this answer to the number of terms of the alternating harmonic series are needed to estimate $\ln(2)$.

Answer: By the alternating series test, $|S_n−S|≤b_{n+1},$ so one needs $10^4$ terms of the alternating harmonic series to estimate $\ln(2)$ to within $0.0001$. The first $10$ partial sums of the series $\displaystyle \sum_{n=1}^∞\frac{1}{n2^n}$ are (up to four decimals) $ 0.5000,0.6250,0.6667,0.6823,0.6885,0.6911,0.6923,0.6928,0.6930,0.6931$ and the tenth partial sum is within $0.0001$ of $\ln(2)=0.6931….$

68) [T] In the text it was stated that a conditionally convergent series can be rearranged to converge to any number. Here is a slightly simpler, but similar, fact. If $a_n≥0$ is such that $a_n→0$ as $n→∞$ but $\displaystyle \sum_{n=1}^∞a_n$ diverges, then, given any number $A$ there is a sequence $s_n$ of $ ±1's$ such that $\displaystyle \sum_{n=1}^∞a_ns_n→A.$ Show this for $A>0$ as follows.

a. Recursively define $s_n$ by $ s_n=1$ if $\displaystyle S_{n−1}=\sum_{k=1}^{n−1}a_ks_k<A$ and $ s_n=−1$ otherwise.

b. Explain why eventually $S_n≥A,$ and for any $m$ larger than this $n$, $A−a_m≤S_m≤A+a_m$.

c. Explain why this implies that $ S_n→A$ as $ n→∞.$

9.6: Ratio and Root Tests

In exercises 1 - 11, use the ratio test to determine whether each series $\displaystyle \sum^∞_{n=1}a_n$ converges or diverges. State if the ratio test is inconclusive.

1) $\displaystyle \sum_{n=1}^∞\frac{1}{n!}$

Answer: $\displaystyle \lim_{n\to \infty}\frac{a_{n+1}}{a_n}=0.$ Converges by the Ratio Test.

2) $\displaystyle \sum_{n=1}^∞\frac{10^n}{n!}$

3) $\displaystyle \sum_{n=1}^∞\frac{n^2}{2^n}$

Answer: $\displaystyle \lim_{n\to \infty} \frac{a_{n+1}}{a_n}=\lim_{n\to \infty}\frac{1}{2}\left(\frac{n+1}{n}\right)^2=\frac{1}{2}<1.$ Converges by the Ratio Test.

4) $\displaystyle \sum_{n=1}^∞\frac{n^{10}}{2^n}$

5) $\displaystyle \sum_{n=1}^∞\frac{(n!)^3}{(3n!)}$

Answer: $\displaystyle \lim_{n\to \infty} \frac{a_{n+1}}{a_n}=\frac{1}{27}<1.$ Converges by the Ratio Test.

6) $\displaystyle \sum_{n=1}^∞\frac{2^{3n}(n!)^3}{(3n!)}$

7) $\displaystyle \sum_{n=1}^∞\frac{(2n)!}{n^{2n}}$

Answer: $\displaystyle \lim_{n\to \infty} \frac{a_{n+1}}{a_n}=\frac{4}{e^2}<1.$ Converges by the Ratio Test.

8) $\displaystyle \sum_{n=1}^∞\frac{(2n)!}{(2n)^n}$

9) $\displaystyle \sum_{n=1}^∞\frac{n!}{(n/e)^n}$

Answer: $\displaystyle \lim_{n\to \infty} \frac{a_{n+1}}{a_n}=1.$ Ratio test is inconclusive.

10) $\displaystyle \sum_{n=1}^∞\frac{(2n)!}{(n/e)^{2n}}$

11) $\displaystyle \sum_{n=1}^∞\frac{(2^nn!)^2}{(2n)^{2n}}$

Answer: $\displaystyle \lim_{n\to \infty} \frac{a_n}{a_{n+1}}=\frac{1}{e^2}<1.$ Converges by the Ratio Test.

In exercises 12 - 21, use the root test to determine whether $\displaystyle \sum^∞_{n=1}a_n$ converges, where $a_n$ is as follows.

12) $\displaystyle a_k=\left(\frac{k−1}{2k+3}\right)^k$

13) $\displaystyle a_k=\left(\frac{2k^2−1}{k^2+3}\right)^k$

Answer: $\displaystyle \lim_{k\to \infty} (a_k)^{1/k}=2>1.$ Diverges by the Root Test.

14) $\displaystyle a_n=\frac{(\ln n)^{2n}}{n^n}$

15) $\displaystyle a_n=n/2^n$

Answer: $\displaystyle \lim_{n\to \infty} (a_n)^{1/n}=1/2<1.$ Converges by the Root Test.

16) $\displaystyle a_n=n/e^n$

17) $\displaystyle a_k=\frac{k^e}{e^k}$

Answer: $\displaystyle \lim_{k\to \infty} (a_k)^{1/k}=1/e<1.$ Converges by the Root Test.

18) $\displaystyle a_k=\frac{π^k}{k^π}$

19) $\displaystyle a_n=\left(\frac{1}{e}+\frac{1}{n}\right)^n$

Answer: $\displaystyle \lim_{n\to \infty} a^{1/n}_n=\lim_{n\to \infty} \frac{1}{e}+\frac{1}{n}=\frac{1}{e}<1.$ Converges by the Root Test.

20) $\displaystyle a_k=\frac{1}{(1+\ln k)^k}$

21) $\displaystyle a_n=\frac{(\ln(1+\ln n))^n}{(\ln n)^n}$

Answer: $\displaystyle \lim_{n\to \infty} a^{1/n}_n= \lim_{n\to \infty} \frac{(\ln(1+\ln n))}{(\ln n)}=0$ by L’Hôpital’s rule. Converges by the Root Test.

In exercises 22 - 28, use either the ratio test or the root test as appropriate to determine whether the series $\displaystyle \sum_{k=1}^∞a_k$ with given terms $a_k$ converges, or state if the test is inconclusive.

22) $\displaystyle a_k=\frac{k!}{1⋅3⋅5⋯(2k−1)}$

23) $\displaystyle a_k=\frac{2⋅4⋅6⋯2k}{(2k)!}$

Answer: $\displaystyle \lim_{k\to \infty} \frac{a_{k+1}}{a_k}= \lim_{k\to \infty} \frac{1}{2k+1}=0.$ Converges by the Ratio Test.

24) $\displaystyle a_k=\frac{1⋅4⋅7⋯(3k−2)}{3^kk!}$

25) $\displaystyle a_n=\left(1−\frac{1}{n}\right)^{n^2}$

Answer: $\displaystyle \lim_{n\to \infty} (a_n)^{1/n}=1/e.$ Converges by the Root Test.

26) $\displaystyle a_k=\left(\frac{1}{k+1}+\frac{1}{k+2}+⋯+\frac{1}{2k}\right)^k$ (Hint: Compare $a^{1/k}_k$ to $\displaystyle ∫^{2k}_k\frac{dt}{t}$.)

27) $\displaystyle a_k=\left(\frac{1}{k+1}+\frac{1}{k+2}+⋯+\frac{1}{3k}\right)^k$

Answer: $\displaystyle \lim_{k\to \infty} a^{1/k}_k=\ln(3)>1.$ Diverges by the Root Test.

28) $\displaystyle a_n=\left(n^{1/n}−1\right)^n$

In exercises 29 - 30, use the ratio test to determine whether $\displaystyle \sum_{n=1}^∞a_n$ converges, or state if the ratio test is inconclusive.

29) $\displaystyle \sum_{n=1}^∞\frac{3^{n^2}}{2^{n^3}}$

Answer: $\displaystyle \lim_{n\to \infty} \left|\frac{a_{n+1}}{a_n}\right|= \lim_{n\to \infty} \frac{3^{2n+1}}{2^{3n^2+3n+1}}=0.$ Converges by the Ratio Test.

30) $\displaystyle \sum_{n=1}^∞\frac{2^{n^2}}{n^nn!}$

In exercises 31, use the root and limit comparison tests to determine whether $\displaystyle \sum_{n=1}^∞a_n$ converges.

31) $\displaystyle \sum_{n=1}^∞\frac{1}{x^n_n}$ where $x_{n+1}=\frac{1}{2}x_n+\dfrac{1}{x_n}, x_1=1$ (Hint: Find limit of ${x_n}$.)

Answer: Converges by the Root Test and Limit Comparison Test since $\displaystyle \lim_{n\to \infty} x_n=\sqrt{2}$.

In exercises 32 - 43, use an appropriate test to determine whether the series converges.

32) $\displaystyle \sum_{n=1}^∞\frac{n+1}{n^3+n^2+n+1}$

33) $\displaystyle \sum_{n=1}^∞\frac{(−1)^{n+1}(n+1)}{n^3+3n^2+3n+1}$

Answer: Converges absolutely by limit comparison with $p$−series, $p=2.$

34) $\displaystyle \sum_{n=1}^∞\frac{(n+1)^2}{n^3+(1.1)^n}$

35) $\displaystyle \sum_{n=1}^∞\frac{(n−1)^n}{(n+1)^n}$

Answer: $\displaystyle \lim_{n→∞}a_n=1/e^2≠0$. Series diverges by the Divergence Test.

36) $\displaystyle a_n=\left(1+\frac{1}{n^2}\right)^n$ (Hint: $(1+\dfrac{1}{n^2})^{n^2}≈e.)$

37) $\displaystyle a_k=1/2^{\sin^2k}$

Answer: Terms do not tend to zero: $a_k≥1/2,$ since $\sin^2x≤1.$

38) $\displaystyle a_k=2^{−\sin(1/k)}$

39) $\displaystyle a_n=1/(^{n+2}_n)$ where $ (^n_k)=\frac{n!}{k!(n−k)!}$

Answer: $a_n=\dfrac{2}{(n+1)(n+2)},$ which converges by comparison with $p$−series for $p=2$.

40) $\displaystyle a_k=1/(^{2k}_k)$

41) $\displaystyle a_k=2^k/(^{3k}_k)$

Answer: $a_k=\dfrac{2^k1⋅2⋯k}{(2k+1)(2k+2)⋯3k}≤(2/3)^k$ converges by comparison with geometric series.

42) $\displaystyle a_k=\left(\frac{k}{k+\ln k}\right)^k$ (Hint: $a_k=\left(1+\dfrac{\ln k}{k}\right)^{−(k/\ln k)\ln k}≈e^{−\ln k}$.)

43) $\displaystyle a_k=\left(\frac{k}{k+\ln k}\right)^{2k}$ (Hint: $a_k=\left(1+\dfrac{\ln k}{k}\right)^{−(k/\ln k)\ln k^2}.)$

Answer: $a_k≈e^{−\ln k^2}=1/k^2.$ Series converges by limit comparison with $p$−series, $p=2.$

The series in exercises 44 - 47 converge by the ratio test. Use summation by parts, $\displaystyle \sum_{k=1}^na_k(b_{k+1}−b_k)=[a_{n+1}b_{n+1}−a_1b_1]−\sum_{k=1}^nb_{k+1}(a_{k+1}−a_k),$ to find the sum of the given series.

44) $\displaystyle \sum_{k=1}^∞\frac{k}{2^k}$ (Hint: Take $a_k=k$ and $b_k=2^{1−k}$.)

45) $\displaystyle \sum_{k=1}^∞\frac{k}{c^k},$ where $c>1$ (Hint: Take $a_k=k$ and $b_k=c^{1−k}/(c−1)$.)

Answer: If $b_k=c^{1−k}/(c−1)$ and $a_k=k$, then $b_{k+1}−b_k=−c^{−k}$ and $\displaystyle \sum_{n=1}^∞\frac{k}{c^k}=a_1b_1+\frac{1}{c−1}\sum_{k=1}^∞c^{−k}=\frac{c}{(c−1)^2}.$

46) $\displaystyle \sum_{n=1}^∞\frac{n^2}{2^n}$

47) $\displaystyle \sum_{n=1}^∞\frac{(n+1)^2}{2^n}$

Answer: $\displaystyle 6+4+1=11$

The $k^{\text{th}}$ term of each of the following series has a factor $x^k$. Find the range of $x$ for which the ratio test implies that the series converges.

48) $\displaystyle \sum_{k=1}^∞\frac{x^k}{k^2}$

49) $\displaystyle \sum_{k=1}^∞\frac{x^{2k}}{k^2}$

Answer: $ |x|≤1$

50) $\displaystyle \sum_{k=1}^∞\frac{x^{2k}}{3^k}$

51) $\displaystyle \sum_{k=1}^∞\frac{x^k}{k!}$

Answer: $ |x|<∞$

52) Does there exist a number $p$ such that $\displaystyle \sum_{n=1}^∞\frac{2^n}{n^p}$ converges?

53) Let $ 0<r<1.$ For which real numbers $p$ does $\displaystyle \sum_{n=1}^∞n^pr^n$ converge?

Answer: All real numbers $p$ by the Ratio Test.

54) Suppose that $\displaystyle \lim_{n→∞}\left|\frac{a_{n+1}}{a_n}\right|=p.$ For which values of $p$ must $\displaystyle \sum_{n=1}^∞2^na_n$ converge?

55) Suppose that $\displaystyle \lim_{n→∞}\left|\frac{a_{n+1}}{a_n}\right|=p.$ For which values of $r>0$ is $\displaystyle \sum_{n=1}^∞r^na_n$ guaranteed to converge?

Answer: $ r<1/p$

56) Suppose that $\left|\dfrac{a_{n+1}}{a_n}\right| ≤(n+1)^p$ for all $n=1,2,…$ where $p$ is a fixed real number. For which values of $p$ is $\displaystyle \sum_{n=1}^∞n!a_n$ guaranteed to converge?

57) For which values of $r>0$, if any, does $\displaystyle \sum_{n=1}^∞r^{\sqrt{n}}$ converge? (Hint: $\displaystyle sum_{n=1}^∞a_n=\sum_{k=1}^∞\sum_{n=k^2}^{(k+1)^2−1}a_n.)$

Answer: $0<r<1.$ Note that the ratio and root tests are inconclusive. Using the hint, there are $2k$ terms $r^\sqrt{n}$ for $ k^2≤n<(k+1)^2$, and for $r<1$ each term is at least $r^k$. Thus, $\displaystyle \sum_{n=1}^∞r^{\sqrt{n}}=\sum_{k=1}^∞\sum_{n=k^2}^{(k+1)^2−1}r^{\sqrt{n}} ≥\sum_{k=1}^∞2kr^k,$ which converges by the ratio test for $r<1$. For $r≥1$ the series diverges by the divergence test.

58) Suppose that $ \left|\dfrac{a_{n+2}}{a_n}\right| ≤r<1$ for all $n$. Can you conclude that $\displaystyle \sum_{n=1}^∞a_n$ converges?

59) Let $a_n=2^{−[n/2]}$ where $ [x]$ is the greatest integer less than or equal to $x$. Determine whether $\displaystyle \sum_{n=1}^∞a_n$ converges and justify your answer.

Answer: One has $\displaystyle a_1=1, a_2=a_3=1/2,…a_{2n}=a_{2n+1}=1/2^n$. The ratio test does not apply because $\displaystyle a_{n+1}/a_n=1$ if $\displaystyle n$ is even. However, $\displaystyle a_{n+2}/a_n=1/2,$ so the series converges according to the previous exercise. Of course, the series is just a duplicated geometric series.

The following advanced exercises use a generalized ratio test to determine convergence of some series that arise in particular applications when tests in this chapter, including the ratio and root test, are not powerful enough to determine their convergence. The test states that if $\displaystyle \lim_{n→∞}\frac{a_{2n}}{a_n}<1/2$, then $\displaystyle \sum a_n$ converges, while if $\displaystyle \lim_{n→∞}\frac{a_{2n+1}}{a_n}>1/2$, then $\displaystyle \sum a_n$ diverges.

60) Let $\displaystyle a_n=\frac{1}{4}\frac{3}{6}\frac{5}{8}⋯\frac{2n−1}{2n+2}=\frac{1⋅3⋅5⋯(2n−1)}{2^n(n+1)!}$. Explain why the ratio test cannot determine convergence of $\displaystyle \sum_{n=1}^∞a_n$. Use the fact that $\displaystyle 1−1/(4k)$ is increasing $\displaystyle k$ to estimate $\displaystyle \lim_{n→∞}\frac{a_{2n}}{a_n}$.

61) Let $\displaystyle a_n=\frac{1}{1+x}\frac{2}{2+x}⋯\frac{n}{n+x}\frac{1}{n}=\frac{(n−1)!}{(1+x)(2+x)⋯(n+x).}$ Show that $a_{2n}/a_n≤e^{−x/2}/2$. For which $x>0$ does the generalized ratio test imply convergence of $\displaystyle \sum_{n=1}^∞a_n$? (Hint: Write $2a_{2n}/a_n$ as a product of $n$ factors each smaller than $1/(1+x/(2n)).)$

Answer: $\displaystyle a_{2n}/a_n=\frac{1}{2}⋅\frac{n+1}{n+1+x}\frac{n+2}{n+2+x}⋯\frac{2n}{2n+x}.$ The inverse of the $\displaystyle kth$ factor is $\displaystyle (n+k+x)/(n+k)>1+x/(2n)$ so the product is less than $\displaystyle (1+x/(2n))^{−n}≈e^{−x/2}.$ Thus for $\displaystyle x>0, \frac{a_{2n}}{a_n}≤\frac{1}{2}e^{−x/2}$. The series converges for $\displaystyle x>0$.

62) Let $a_n=\dfrac{n^{\ln n}}{(\ln n)^n}.$ Show that $ \dfrac{a_{2n}}{a_n}→0$ as $n→∞.$

Chapter Review Exercises

True or False? Justify your answer with a proof or a counterexample.

1) If $\displaystyle \lim_{n→∞}a_n=0,$ then $\displaystyle \sum_{n=1}^∞a_n$ converges.

Solution: false

2) If $\displaystyle \lim_{n→∞}a_n≠0,$ then $\displaystyle \sum_{n=1}^∞a_n$ diverges.

3) If $\displaystyle \sum_{n=1}^∞|a_n|$ converges, then $\displaystyle \sum_{n=1}^∞a_n$ converges.

Solution: true

4) If $\displaystyle \sum_{n=1}^∞2^na_n$ converges, then $\displaystyle \sum_{n=1}^∞(−2)^na_n$ converges.

Is the sequence bounded, monotone, and convergent or divergent? If it is convergent, find the limit.

5) $\displaystyle a_n=\frac{3+n^2}{1−n}$

Solution: unbounded, not monotone, divergent

6) $\displaystyle a_n=ln(\frac{1}{n})$

7) $\displaystyle a_n=\frac{ln(n+1)}{\sqrt{n+1}}$

Solution: bounded, monotone, convergent, $\displaystyle 0$

8) $\displaystyle a_n=\frac{2^{n+1}}{5^n}$

9) $\displaystyle a_n=\frac{\ln(\cos n)}{n}$

Solution: unbounded, not monotone, divergent

Is the series convergent or divergent?

10) $\displaystyle \sum_{n=1}^∞\frac{1}{n^2+5n+4}$

11) $\displaystyle \sum_{n=1}^∞ln(\frac{n+1}{n})$

Solution: diverges

12) $\displaystyle \sum_{n=1}^∞\frac{2^n}{n^4}$

13) $\displaystyle \sum_{n=1}^∞\frac{e^n}{n!}$

Solution: converges

14) $\displaystyle \sum_{n=1}^∞n^{−(n+1/n)}$

Is the series convergent or divergent? If convergent, is it absolutely convergent?

15) $\displaystyle \sum_{n=1}^∞\frac{(−1)^n}{\sqrt{n}}$

Solution: converges, but not absolutely

16) $\displaystyle \sum_{n=1}^∞\frac{(−1)^nn!}{3^n}$

17) $\displaystyle \sum_{n=1}^∞\frac{(−1)^nn!}{n^n}$

Solution: converges absolutely

18) $\displaystyle \sum_{n=1}^∞sin(\frac{nπ}{2})$

19) $\displaystyle \sum_{n=1}^∞cos(πn)e^{−n}$

Solution: converges absolutely

Evaluate

20) $\displaystyle \sum_{n=1}^∞\frac{2^{n+4}}{7^n}$

21) $\displaystyle \sum_{n=1}^∞\frac{1}{(n+1)(n+2)}$

Solution: $\displaystyle \frac{1}{2}$

22) A legend from India tells that a mathematician invented chess for a king. The king enjoyed the game so much he allowed the mathematician to demand any payment. The mathematician asked for one grain of rice for the first square on the chessboard, two grains of rice for the second square on the chessboard, and so on. Find an exact expression for the total payment (in grains of rice) requested by the mathematician. Assuming there are $\displaystyle 30,000$ grains of rice in $\displaystyle 1$ pound, and $\displaystyle 2000$ pounds in $\displaystyle 1$ ton, how many tons of rice did the mathematician attempt to receive?

The following problems consider a simple population model of the housefly, which can be exhibited by the recursive formula $\displaystyle x_{n+1}=bx_n$, where $\displaystyle x_n$ is the population of houseflies at generation $\displaystyle n$, and $\displaystyle b$ is the average number of offspring per housefly who survive to the next generation. Assume a starting population $\displaystyle x_0$.

23) Find $\displaystyle \lim_{n→∞}x_n$ if $\displaystyle b>1, b<1$, and $\displaystyle b=1.$

Solution: $\displaystyle ∞, 0, x_0$

24) Find an expression for $\displaystyle S_n=\sum_{i=0}^nx_i$ in terms of $\displaystyle b$ and $\displaystyle x_0$. What does it physically represent?

25) If $\displaystyle b=\frac{3}{4}$ and $\displaystyle x_0=100$, find $\displaystyle S_{10}$ and $\displaystyle \lim_{n→∞}S_n$

Solution: $\displaystyle S_{10}≈383, \lim_{n→∞}S_n=400$

26) For what values of $\displaystyle b$ will the series converge and diverge? What does the series converge to?

Contributors and Attributions

Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.