5.1: Decimals (Part 1)
- Page ID
- 4998
- Name decimals
- Write decimals
- Convert decimals to fractions or mixed numbers
- Locate decimals on the number line
- Order decimals
- Round decimals
Before you get started, take this readiness quiz.
- Name the number 4,926,015 in words. If you missed this problem, review Example 1.1.4.
- Round 748 to the nearest ten. If you missed this problem, review Example 1.2.9.
- Locate \(\dfrac{3}{10}\) on a number line. If you missed this problem, review Example 4.2.16.
Name Decimals
You probably already know quite a bit about decimals based on your experience with money. Suppose you buy a sandwich and a bottle of water for lunch. If the sandwich costs $3.45, the bottle of water costs $1.25, and the total sales tax is $0.33, what is the total cost of your lunch?
\[\begin{split} & $3.45 \qquad Sandwich \\ & $1.25 \qquad Water \\ + & $0.33 \qquad Tax \\ \hline & $5.03 \qquad Total \end{split}\]
The total is $5.03. Suppose you pay with a $5 bill and 3 pennies. Should you wait for change? No, $5 and 3 pennies is the same as $5.03.
Because 100 pennies = $1, each penny is worth \(\dfrac{1}{100}\) of a dollar. We write the value of one penny as $0.01, since 0.01 = \(\dfrac{1}{100}\).
Writing a number with a decimal is known as decimal notation. It is a way of showing parts of a whole when the whole is a power of ten. In other words, decimals are another way of writing fractions whose denominators are powers of ten. Just as the counting numbers are based on powers of ten, decimals are based on powers of ten. Table \(\PageIndex{1}\) shows the counting numbers.
| Counting number | Name |
|---|---|
| 1 | One |
| 10 = 10 | Ten |
| 10 • 10 = 100 | One hundred |
| 10 • 10 • 10 = 1000 | One thousand |
| 10 • 10 • 10 • 10 = 10,000 | Ten thousand |
How are decimals related to fractions? Table \(\PageIndex{2}\) shows the relation.
| Decimal | Fraction | Name |
|---|---|---|
| 0.1 | \(\dfrac{1}{10}\) | One tenth |
| 0.01 | \(\dfrac{1}{100}\) | One hundredth |
| 0.001 | \(\dfrac{1}{1000}\) | One thousandth |
| 0.0001 | \(\dfrac{1}{10,000}\) | One ten-thousandth |
When we name a whole number, the name corresponds to the place value based on the powers of ten. In Whole Numbers, we learned to read 10,000 as ten thousand. Likewise, the names of the decimal places correspond to their fraction values. Notice how the place value names in Figure \(\PageIndex{1}\) relate to the names of the fractions from Table \(\PageIndex{2}\).
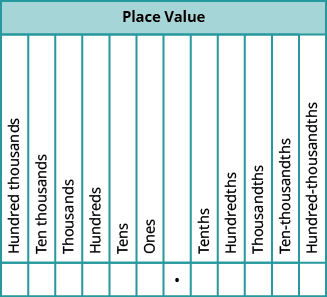
Figure \(\PageIndex{1}\) - This chart illustrates place values to the left and right of the decimal point.
Notice two important facts shown in Figure \(\PageIndex{1}\).
- The “th” at the end of the name means the number is a fraction. “One thousand” is a number larger than one, but “one thousandth” is a number smaller than one.
- The tenths place is the first place to the right of the decimal, but the tens place is two places to the left of the decimal.
Remember that $5.03 lunch? We read $5.03 as five dollars and three cents. Naming decimals (those that don’t represent money) is done in a similar way. We read the number 5.03 as five and three hundredths.
We sometimes need to translate a number written in decimal notation into words. As shown in Figure \(\PageIndex{2}\), we write the amount on a check in both words and numbers.

Figure \(\PageIndex{2}\) - When we write a check, we write the amount as a decimal number as well as in words. The bank looks at the check to make sure both numbers match. This helps prevent errors.
| Let’s try naming a decimal, such as 15.68. | |
| We start by naming the number to the left of the decimal. | fifteen______ |
| We use the word “and” to indicate the decimal point. | fifteen and_____ |
| Then we name the number to the right of the decimal point as if it were a whole number. | fifteen and sixty-eight_____ |
| Last, name the decimal place of the last digit. | fifteen and sixty-eight hundredths |
The number 15.68 is read fifteen and sixty-eight hundredths.
- Name the number to the left of the decimal point.
- Write “and” for the decimal point.
- Name the “number” part to the right of the decimal point as if it were a whole number.
- Name the decimal place of the last digit.
Name each decimal: (a) 4.3 (b) 2.45 (c) 0.009 (d) −15.571.
Solution
(a) 4.3
| Name the number to the left of the decimal point. | four_____ |
| Write "and" for the decimal point. | four and_____ |
| Name the number to the right of the decimal point as if it were a whole number. | four and three_____ |
| Name the decimal place of the last digit. | four and three tenths |
(b) 2.45
| Name the number to the left of the decimal point. | two_____ |
| Write "and" for the decimal point. | two and_____ |
| Name the number to the right of the decimal point as if it were a whole number. | two and forty-five_____ |
| Name the decimal place of the last digit. | two and forty-five hundredths |
(c) 0.009
| Name the number to the left of the decimal point. | Zero is the number to the left of the decimal; it is not included in the name. |
| Name the number to the right of the decimal point as if it were a whole number. | nine_____ |
| Name the decimal place of the last digit. | nine thousandths |
(d) −15.571
| Name the number to the left of the decimal point. | negative fifteen |
| Write "and" for the decimal point. | negative fifteen and_____ |
| Name the number to the right of the decimal point as if it were a whole number. | negative fifteen and five hundred seventyone_____ |
| Name the decimal place of the last digit. | negative fifteen and five hundred seventyone thousandths |
Name each decimal: (a) 6.7 (b) 19.58 (c) 0.018 (d) −2.053
- Answer a
-
six and seven tenths
- Answer b
-
nineteen and fifty-eight hundredths
- Answer c
-
eighteen thousandths
- Answer d
-
negative two and fifty-three thousandths
Name each decimal: (a) 5.8 (b) 3.57 (c) 0.005 (d) −13.461
- Answer a
-
five and eight tenths three and fifty-seven hundredths
- Answer b
-
three and fifty-seven hundredths
- Answer c
-
five thousandths
- Answer d
-
negative thirteen and four hundred sixty-one thousandths
Write Decimals
Now we will translate the name of a decimal number into decimal notation. We will reverse the procedure we just used. Let’s start by writing the number six and seventeen hundredths:
| The word and tells us to place a decimal point. | ___.___ |
| The word before and is the whole number; write it to the left of the decimal point. | 6._____ |
| The decimal part is seventeen hundredths. Mark two places to the right of the decimal point for hundredths. | 6._ _ |
| Write the numerals for seventeen in the places marked. | 6.17 |
Write fourteen and thirty-seven hundredths as a decimal.
Solution
| Place a decimal point under the word ‘and’. | ______. _________ |
| Translate the words before ‘and’ into the whole number and place it to the left of the decimal point. | 14. _________ |
| Mark two places to the right of the decimal point for “hundredths”. | 14.__ __ |
| Translate the words after “and” and write the number to the right of the decimal point. | 14.37 |
Fourteen and thirty-seven hundredths is written 14.37.
Write as a decimal: thirteen and sixty-eight hundredths.
- Answer
-
13.68
Write as a decimal: five and eight hundred ninety-four thousandths.
- Answer
-
5.894
Step 1. Look for the word “and”—it locates the decimal point.
Step 2. Mark the number of decimal places needed to the right of the decimal point by noting the place value indicated by the last word.
- Place a decimal point under the word “and.” Translate the words before “and” into the whole number and place it to the left of the decimal point.
- If there is no “and,” write a “0” with a decimal point to its right.
Step 3. Translate the words after “and” into the number to the right of the decimal point. Write the number in the spaces—putting the final digit in the last place.
Step 4. Fill in zeros for place holders as needed.
The second bullet in Step 2 is needed for decimals that have no whole number part, like ‘nine thousandths’. We recognize them by the words that indicate the place value after the decimal – such as ‘tenths’ or ‘hundredths.’ Since there is no whole number, there is no ‘and.’ We start by placing a zero to the left of the decimal and continue by filling in the numbers to the right, as we did above.
Write twenty-four thousandths as a decimal.
Solution
| Look for the word "and". | There is no "and" so start with 0. |
| To the right of the decimal point, put three decimal places for thousandths. |  |
| Write the number 24 with the 4 in the thousandths place. |  |
| Put zeros as placeholders in the remaining decimal places. | 0.024 |
So, twenty-four thousandths is written 0.024
Write as a decimal: fifty-eight thousandths.
- Answer
-
0.058
Write as a decimal: sixty-seven thousandths.
- Answer
-
0.067
Before we move on to our next objective, think about money again. We know that $1 is the same as $1.00. The way we write $1 (or $1.00) depends on the context. In the same way, integers can be written as decimals with as many zeros as needed to the right of the decimal.
\[\begin{split} 5 & = 5.0 \qquad \quad -2 = -2.0 \\ 5 & = 5.00 \qquad \; \; -2 = -2.00 \\ 5 & = 5.000 \qquad -2 = -2.000 \\ & \qquad \qquad and \; so \; on \ldots \end{split}\]
Convert Decimals to Fractions or Mixed Numbers
We often need to rewrite decimals as fractions or mixed numbers. Let’s go back to our lunch order to see how we can convert decimal numbers to fractions. We know that $5.03 means 5 dollars and 3 cents. Since there are 100 cents in one dollar, 3 cents means \(\dfrac{3}{100}\) of a dollar, so 0.03 = \(\dfrac{3}{100}\).
We convert decimals to fractions by identifying the place value of the farthest right digit. In the decimal 0.03, the 3 is in the hundredths place, so 100 is the denominator of the fraction equivalent to 0.03.
\[0.03 = \dfrac{3}{100} \nonumber\]
For our $5.03 lunch, we can write the decimal 5.03 as a mixed number.
\[5.03 = 5 \dfrac{3}{100} \nonumber\]
Notice that when the number to the left of the decimal is zero, we get a proper fraction. When the number to the left of the decimal is not zero, we get a mixed number.
Step 1. Look at the number to the left of the decimal.
- If it is zero, the decimal converts to a proper fraction.
- If it is not zero, the decimal converts to a mixed number.
- Write the whole number.
Step 2. Determine the place value of the final digit.
Step 3. Write the fraction.
- numerator—the ‘numbers’ to the right of the decimal point
- denominator—the place value corresponding to the final digit
Step 4. Simplify the fraction, if possible.
Write each of the following decimal numbers as a fraction or a mixed number: (a) 4.09 (b) 3.7 (c) −0.286
Solution
(a) 4.09
| There is a 4 to the left of the decimal point. Write "4" as the whole number part of the mixed number. |  |
| Determine the place value of the final digit. |  |
| Write the fraction. Write 9 in the numerator as it is the number to the right of the decimal point. |  |
| Write 100 in the denominator as the place value of the final digit, 9, is hundredth. | \(4 \dfrac{9}{100}\) |
| The fraction is in simplest form. | So, 4.09 = \(4 \dfrac{9}{100}\) |
Did you notice that the number of zeros in the denominator is the same as the number of decimal places?
(b) 3.7
| There is a 3 to the left of the decimal point. Write "3" as the whole number part of the mixed number. |  |
| Determine the place value of the final digit. |  |
| Write the fraction. Write 7 in the numerator as it is the number to the right of the decimal point. |  |
| Write 10 in the denominator as the place value of the final digit, 7, is tenths. | \(3 \dfrac{7}{10}\) |
| The fraction is in simplest form. | So, 3.7 = \(3 \dfrac{7}{10}\) |
(c) −0.286
| There is a 0 to the left of the decimal point. Write a negative sign before the fraction. |  |
| Determine the place value of the final digit and write it in the denominator. |  |
| Write the fraction. Write 286 in the numerator as it is the number to the right of the decimal point. Write 1,000 in the denominator as the place value of the final digit, 6, is thousandths. | \(- \dfrac{286}{1000}\) |
| We remove a common factor of 2 to simplify the fraction. | \(- \dfrac{143}{500}\) |
Write as a fraction or mixed number. Simplify the answer if possible. (a) 5.3 (b) 6.07 (c) −0.234
- Answer a
-
\(5 \frac{3}{10}\)
- Answer b
-
\(6 \frac{7}{100}\)
- Answer c
-
\(-\frac{234}{1000}\)
Write as a fraction or mixed number. Simplify the answer if possible. (a) 8.7 (b) 1.03 (c) −0.024
- Answer a
-
\(8 \frac{7}{10}\)
- Answer b
-
\(1 \frac{3}{100}\)
- Answer c
-
\(- \frac{24}{1000}\)
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


