1.7: Tangent Planes and Normal Lines
- Page ID
- 602
Tangent Planes
Let \(z = f(x,y)\) be a function of two variables. We can define a new function \(F(x,y,z)\) of three variables by subtracting \(z\). This has the condition
\[ F(x,y,z) = 0.\nonumber \]
Now consider any curve defined parametrically by
\[x = x(t), \;\;\; y = y(t), \;\;\; z = z(t).\nonumber \]
We can write,
\[F(x(t), y(t), z(t)) = 0.\nonumber \]
Differentiating both sides with respect to \(t\), and using the chain rule gives
\[F_x(x, y, z) x' + F_y(x, y, z) y' + F_z(x, y, z) z' = 0\nonumber \]
Notice that this is the dot product of the gradient function and the vector \(\langle x',y',z'\rangle \),
\[\nabla F \cdot \langle x', y', z'\rangle = 0.\nonumber \]
In particular the gradient vector is orthogonal to the tangent line of any curve on the surface. This leads to:
Definition: Tangent Plane
Let \(F(x,y,z)\) define a surface that is differentiable at a point \((x_0,y_0,z_0)\), then the tangent plane to \(F ( x, y, z )\) at \(( x_0, y_0, z_0)\) is the plane with normal vector
\[ \nabla \, F(x_0,y_0,z_0) \nonumber \]
that passes through the point \((x_0,y_0,z_0)\). In particular, the equation of the tangent plane is
\[ \nabla \, F(x_0,y_0,z_0) \cdot \langle x - x_0 , y - y_0 , z - z_0 \rangle = 0. \nonumber \]
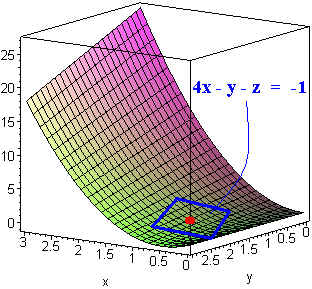
Example \(\PageIndex{1}\)
Find the equation of the tangent plane to
\[ z = 3x^2 - xy \nonumber \]
at the point \((1,2,1)\).
Solution
We let
\[F(x,y,z) = 3x^2 - xy - z\nonumber \]
then
\[\nabla F = \langle 6x - y, -x, -1\rangle . \nonumber \]
At the point \((1,2,1)\), the normal vector is
\[\nabla F(1,2,1) = \langle 4, -1, -1\rangle . \nonumber \]
Now use the point normal formula for a plan
\[\langle 4, -1, -1\rangle \cdot \langle x - 1, y - 2, z - 1\rangle = 0\nonumber \]
or
\[4(x - 1) - (y - 2) - (z - 1) = 0.\nonumber \]
Finally we get
\[ 4x - y - z = 1.\nonumber \]
Normal Lines
Given a vector and a point, there is a unique line parallel to that vector that passes through the point. In the context of surfaces, we have the gradient vector of the surface at a given point. This leads to the following definition.
Definition: Normal Line
Let \(F(x,y,z)\) define a surface that is differentiable at a point \((x_0,y_0,z_0)\), then the normal line to \(F(x,y,z)\) at \((x_0,y_0,z_0)\) is the line with normal vector
\[ \nabla \, F(x_0,y_0,z_0) .\nonumber \]
that passes through the point \((x_0,y_0,z_0)\). In Particular the equation of the normal line is
\[ x(t) = x_0 + F_x(x_0,y_0,z_0) t, \nonumber \]
\[ y(t) = y_0 + F_y(x_0,y_0,z_0) t, \nonumber \]
\[ z(t) = z_0 + F_z(x_0,y_0,z_0) t. \nonumber \]
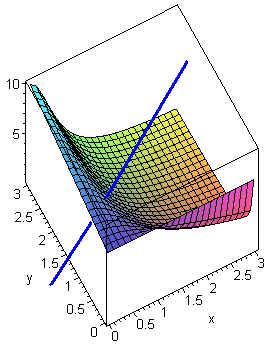
Example \(\PageIndex{2}\)
Find the parametric equations for the normal line to
\[ x^2yz - y + z - 7 = 0 \nonumber \]
at the point \((1,2,3)\).
Solution
We compute the gradient:
\[\nabla F = \langle 2xyz, x^2z - 1, x^2y + 1\rangle = \langle 12, 2, 3\rangle .\nonumber \]
Now use the formula to find
\[x(t) = 1 + 12t, \;\;\; y(t) = 2 + 2t, \;\;\; z(t) = 3 + 3t.\nonumber \]
The diagram below displays the surface and the normal line.
Angle of Inclination
Given a plane with normal vector n the angle of inclination, \(q\) is defined by
\[\cos q = \dfrac{|\textbf{n} \cdot k|}{ ||\textbf{n} ||}. \nonumber \]
More generally, if \( F(x,y,z) = 0 \) is a surface, then the angle of inclination at the point \((x_0,y_0,z_0)\) is defined by the angle of inclination of the tangent plane at the point with
\[ \cos\,q = \dfrac{ | \nabla F(x_0, y_0, z_0) \cdot \textbf{k}| }{|| \nabla F(x_0, y_0, z_0)||}. \nonumber \]
Example \(\PageIndex{3}\)
Find the angle of inclination of
\[ \dfrac{x^2}{4} + \dfrac{y^2}{4} + \dfrac{z^2}{8} = 1\nonumber \]
at the point \((1,1,2)\).
Solution
First compute
\[ \nabla F = \langle \dfrac{x}{2}, \dfrac{y}{2}, \dfrac{z}{4}\rangle .\nonumber \]
Now plug in to get
\[\nabla F(1,1,2) = \langle \dfrac{1}{2}, \dfrac{1}{2}, \dfrac{1}{2} \rangle .\nonumber \]
We have
\[|\langle \dfrac{1}{2} , \dfrac{1}{2} , \dfrac{1}{2} \rangle \cdot \hat{\textbf{k}} | = \dfrac{1}{2} .\nonumber \]
Also,
\[||\langle \dfrac{1}{2} , \dfrac{1}{2} , \dfrac{1}{2} \rangle || = \dfrac{\sqrt{3}}{2} .\nonumber \]
Hence
\[ \cos q = \dfrac{\frac{1}{2}}{( \frac{\sqrt{3}}{2} )} = \dfrac{1}{\sqrt{3}} . \nonumber \]
So the angle of inclination is
\[q = \cos^{-1}(\dfrac{1}{\sqrt{3}}) = 0.955 \text{ radians} .\nonumber \]
The Tangent Line to a Curve
Example \(\PageIndex{4}\)
Find the tangent line to the curve of intersection of the sphere
\[x^2 + y^2 + z^2 = 30\nonumber \]
and the paraboloid
\[z = x^2 + y^2\nonumber \]
at the point \((1,2,5)\).
Solution
We find the gradient of the two surfaces at the point
\[ \nabla(x^2 + y^2 + z^2) = \langle 2x, 2y, 2z\rangle = \langle 2, 4,10\rangle \nonumber \]
and
\[\nabla (x^2 + y^2 - z) = \langle 2x, 2y, -1\rangle = \langle 2, 4, -1\rangle .\nonumber \]
These two vectors will both be perpendicular to the tangent line to the curve at the point, hence their cross product will be parallel to this tangent line. We compute
\[ \begin{vmatrix} \hat{\textbf{i}} & \hat{\textbf{j}} & \hat{\textbf{k}} \\ 2 & 4 & 10 \\ 2 & 4 & -1 \end{vmatrix} = -44 \hat{\textbf{i}} + 22 \hat{\textbf{j}}. \nonumber \]
Hence the equation of the tangent line is
\[x(t) = 1 - 44t y(t) = 2 + 22t z(t) = 5.\nonumber \]
Contributors and Attributions
- Larry Green (Lake Tahoe Community College)
Integrated by Justin Marshall.


