3.00: Physical Problems for Nonlinear Equations
( \newcommand{\kernel}{\mathrm{null}\,}\)
Lesson 1: General Engineering
Summary
Finding the depth to which a ball would float in water requires solving a nonlinear equation.
Modeling
You are working for ‘DOWN THE TOILET COMPANY’ that makes floats for ABC commodes. The ball has a specific gravity of 0.6 and has a radius of 5.5 cm. You are asked to find the depth to which the ball will get submerged when floating in water (see Figure 3.0.1.1).

According to Newton’s third law of motion, every action has an equal and opposite reaction. In this case, the weight of the ball is balanced by the buoyancy force (Figure 3.0.1.2).
Weight of ball=Buoyancy force(3.0.1.1)
The weight of the ball is given by
Weight of ball=(Volume of ball)×(Density of ball)×(Acceleration due to gravity)=(43πR3)(ρb)(g)(3.0.1.2)
where
R=radius of the ball (m),
ρ=density of the ball (kg/m3),
g=acceleration due to gravity (m/s2).
The buoyancy force is given by
Buoyancy force=Weight of water displaced=(Volume of the ball under water) (Density of water)(Acceleration due to gravity)=πx2(R−x3)ρwg(3.0.1.3)
where
x=depth to which ball is submerged,
ρw=density of water.

Now substituting Equations (3.0.1.2) and (3.0.1.3) in Equation (3.0.1.1),
43πR3ρbg=πx2(R−x3)ρwg
4R3ρb=3x2(R−x3)ρw
4R3ρb−3x2Rρw+x3ρw=0
4R3ρbρw−3x2R+x3=0
4R3γb−3x2R+x3=0(3.0.1.4)
where
the specific gravity of the ball, γb, is given by
γb=ρbρw(3.0.1.5)
Given
R=5.5 cm=0.055 m,
γb=0.6, and
substituting in Equation (3.0.1.4), we get
4(0.055)3(0.6)−3x2(0.055)+x3=0
3.993×10−4−0.165x2+x3=0(3.0.1.6)
Equation (3.0.1.6) is nonlinear. Solving it would give us the value of x, that is, the depth to which the ball is submerged underwater.
Appendix: Derivation of the formula for the volume of a ball submerged underwater
How do you find that the volume of the ball submerged underwater as given by
V=πh2(3r−h)3(3.0.1.7)
where
r=radius of the ball,
h=height of the ball to which the ball is submerged.
From calculus,
V=∫rr−hAdx(3.0.1.8)
where A is the cross-sectioned area at a distance x from the center of the sphere. The lower limit of integration is x=r−h as that is where the water line is
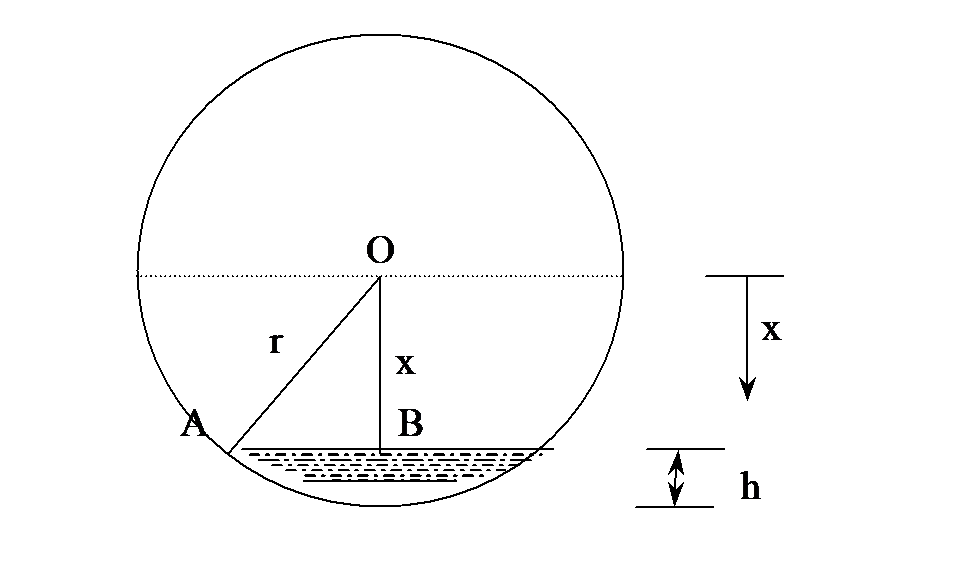
and the upper limit is r as that is the bottom of the sphere. So, what is the A at any location x?
From Figure 3.0.1.3, for a location x,
OB=x,
OA=r,
then AB=√OA2−OB2=√r2−x2(3.0.1.9)
and AB is the radius of the area at x. So the cross-sectional area at location B is
A=π(AB)2=π(r2−x2)(3.0.1.10)
so
V=∫rr−hπ(r2−x2)dx=π(r2x−x33)rr−h=π[(r2r−r33)−(r2(r−h)−(r−h)33)]=πh2(3r−h)3.(3.0.1.11)
Lesson 2: Mechanical Engineering
Summary
A physical problem of finding how much cooling a shaft needs to be shrink fit into a hollow hub. The temperature to which the cooling needs to be done is modeled as a nonlinear equation.
Modeling
To make the fulcrum (Figure 3.0.2.1) of a bascule bridge, a long hollow steel shaft called the trunnion is shrink fit into a steel hub. The resulting steel trunnion-hub assembly is then shrink fit into the girder of the bridge.


This is done by first immersing the trunnion in a cold medium such as dry-ice/alcohol mixture. After the trunnion reaches the steady state temperature of the cold medium, the trunnion outer diameter contracts. The trunnion is taken out of the medium and slid through the hole of the hub (Figure 3.0.2.2).

When the trunnion heats up, it expands and creates an interference fit with the hub. In 1995, on one of the bridges in Florida, this assembly procedure did not work as designed. Before the trunnion could be inserted fully into the hub, the trunnion got stuck. So a new trunnion and hub had to be ordered at a cost of $50,000. Coupled with construction delays, the total loss was more than a hundred thousand dollars.
Why did the trunnion get stuck? This was because the trunnion had not contracted enough to slide through the hole.
Now the same designer is working on making the fulcrum for another bascule bridge. Can you help them not to make the same mistake?
For this new bridge, the designer needs to fit a hollow trunnion of the outside diameter 12.363′′ in a hub of an inner diameter 12.358′′ and plans to put the trunnion in dry-ice/alcohol mixture (temperature of the fluid - dry ice/alcohol mixture is −108∘F) to contract the trunnion so that it can be slid through the hole of the hub. To slide the trunnion without sticking also requires a diametrical clearance of at least 0.01′′ between the trunnion and the hub. Assuming the room temperature is 80∘F, is immersing it in a dry-ice/alcohol mixture a correct decision? To what temperature does the designer need to cool the trunnion to get the desired contraction?
Looking at the designer’s record for the previous bridge (where the trunnion got stuck in the hub), it was found that they used the coefficient of linear thermal expansion at room temperature to calculate the contraction in the trunnion diameter. In that case, the reduction, ΔD in the outer diameter of the trunnion is
ΔD=DαΔT(3.0.2.1)
where
D=outer diameter of the trunnion,
α=coefficient of linear thermal expansion at room temperature, and
ΔT=change in temperature,
Given
D=12.363′′
α=6.817×10−6in/in/∘F at 80∘F
ΔT=Tfluid−Troom=−108−80=−188∘F
where
Tfluid=temperature of dry-ice/alcohol mixture
Troom=room temperature
the reduction in the trunnion outer diameter is given by
ΔD=(12.363)(6.47×10−6)(−188)=−0.01504′′
So the trunnion is predicted to reduce in diameter by 0.01504′′. But is this enough reduction in diameter? As per specifications, the designer needs the trunnion to contract by
=trunnion outside diameter−hub inner diameter+diametral clearance=12.363′′−12.358′′+0.01′′=0.015′′
So, according to the calculations, immersing the steel trunnion in dry-ice/alcohol mixture gives the desired contraction of 0.015′′ as the predicted contraction is 0.01504′′.
But as shown in Figure 3.0.2.3, the coefficient of linear thermal expansion of steel decreases with temperature and is not constant over the range of temperature the trunnion goes through. Hence the above formula (Equation 3.0.2.1) would overestimate the thermal contraction. This assumption is the mistake the designer made in the calculations for the earlier bridge.

The contraction in the diameter for the trunnion for which the coefficient of linear thermal expansion varies as a function of temperature is given by
ΔD=D∫TfluidTroomαdT(3.0.2.2)
Note that Equation (3.0.2.2) reduces to Equation (3.0.2.1) if the coefficient of linear thermal expansion is assumed to be constant. In Figure 3.0.2.3, the coefficient of linear thermal expansion of typical cast steel is approximated by a second-order polynomial as
α=−1.2278×10−11T2+6.1946×10−9T+6.0150×10−6(3.0.2.3)
Since the desired contraction is at least 0.015′′, that is,
ΔD=−0.015′′,(3.0.2.4)
From Equations (3.0.2.2), (3.0.2.3), and (3.0.2.4),
−0.015=12.363∫Tfluid80(−1.2278×10−11T2+6.1946×10−9T+6.015×10−6)dT
−0.015=12.363[−1.2278×10−11T33+6.1946×10−9T22+6.015×10−6T]Tfluid80
−0.015=12.363(−0.40927×10−11T3fluid+0.30973×10−8T2fluid+0.60150×10−5Tfluid−0.49893×10−3)
f(Tf)=−0.50598×10−10T3f+0.38292×10−7T2f+0.74363×10−4Tf+0.88318×10−2=0(3.0.2.5)
One can solve this nonlinear equation to find the minimum fluid temperature needed to cool down the trunnion and get the desired contraction. Is cooling in dry-ice/alcohol mixture still your recommendation? You may be surprised that it would not be the correct decision to make.

