3.03: Bisection Methods for Solving a Nonlinear Equation

Lesson 1: Background of Bisection Method

Learning Objectives

After successful completion of this lesson, you should be able to

1) articulate the background to the bisection method

Introduction

One of the first numerical methods developed to find the root of a nonlinear equation $f(x) = 0$ was the bisection method (also called the binary-search method). The procedure is based on the following theorem.

Theorem

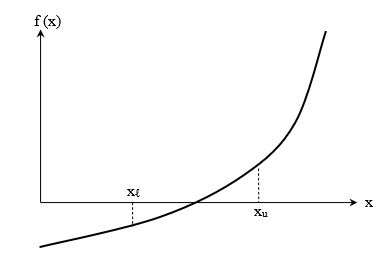
An equation$f(x) = 0$, where $f(x)$ is a real continuous function, has at least one root between $x_{l}$ and $x_{u}$ if $f(x_{l})f(x_{u}) < 0$ (See Figure $\PageIndex{1.1}$).

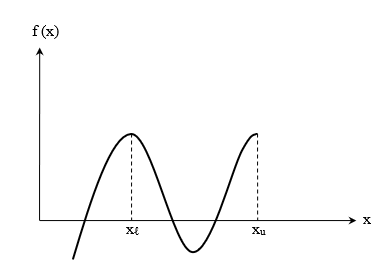
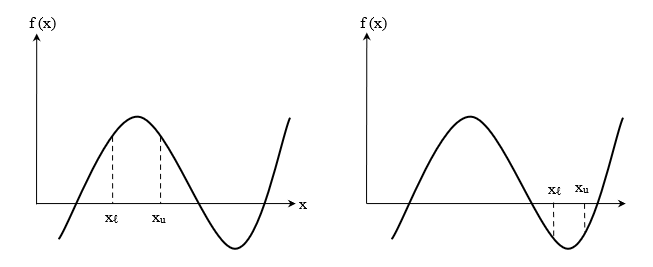
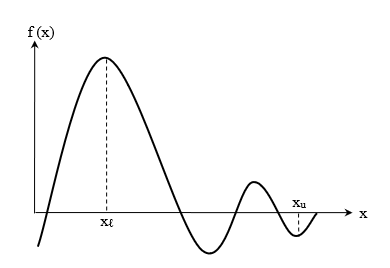
Note that if $f(x_{l})f(x_{u}) > 0$, there may or may not be any root between $x_{l}$ and $x_{u}$ (Figures $\PageIndex{1.2}$ and $\PageIndex{1.3}$). If $f(x_{l})f(x_{u}) < 0$, then there may be more than one root between $x_{l}$ and $x_{u}$ (Figure $\PageIndex{1.4}$). So the theorem only guarantees one root between $x_{l}$ and $x_{u}$.

Since the method is based on finding the root between two points, the technique falls under bracketing methods.

Since the root is bracketed between two points, $x_{l}$ and $x_{u}$, one can find the midpoint $x_{m}$ between $x_{l}$ and $x_{u}$. We hence get two new intervals $x_{l}$ and $x_{m}$, and $x_{m}$ and $x_{u}$.

Figure $\PageIndex{1.1}$. At least one root exists between the two points if the function is real, continuous, and changes sign.

Figure $\PageIndex{1.2}$. If the function $f(x)$ does not change the sign between the two points, roots of the equation $f(x) = 0$ may still exist between the two points.

Figure $\PageIndex{1.3}$. If the function $f(x)$ does not change the sign between two points, there may not be any roots for the equation $f(x) = 0$ between the two points.

Figure $\PageIndex{1.4}$. If the function $f(x)$ changes the sign between the two points, more than one root for the equation $f(x) = 0$ may exist between the two points.

Is the root now between $x_{l}$ and $x_{m}$ or between $x_{m}$ and $x_{u}$? Well, one can find the sign of $f(x_{l})f(x_{m})$, and if $f(x_{l})f(x_{m}) < 0$ then the new bracket is between $x_{l}$ and $x_{m}$; otherwise, it is between $x_{m}$ and $x_{u}$. So, you can see that you are halving the interval. As one repeats this process, the width of the interval $\left\lbrack x_{l},x_{u} \right\rbrack$ becomes smaller and smaller, and you can zero on to the root of the equation $f(x) = 0$.

Audiovisual Lectures

Title: Bisection Method - Introduction

Summary: Learn what the bisection method of solving nonlinear equations is based on.

Lesson 2: Bisection Method Algorithm

Learning Objectives

After successful completion of this lesson, you should be able to

1) write the algorithm for the bisection method of solving a nonlinear equation.

What is the bisection method, and what is it based on?

One of the first numerical methods developed to find the root of a nonlinear equation $f(x) = 0$ was the bisection method (also called the binary-search method). The procedure is based on the following theorem.

Theorem

An equation$f(x) = 0$, where $f(x)$ is a real continuous function, has at least one root between $x_{l}$ and $x_{u}$ if $f(x_{l})f(x_{u}) < 0$ (See Figure $\PageIndex{2.1}$).

Figure $\PageIndex{2.1}$. At least one root exists between the two points if the function is real, continuous, and changes sign.

Bisection method

Since the method is based on finding the root between two points, the technique falls under the category of bracketing methods.

Since the root is bracketed between two points, $x_{l}$ and $x_{u}$, one can find the mid-point, $x_{m}$ between $x_{l}$ and $x_{u}$. This gives us two new intervals $x_{l}$ and $x_{m}$, and $x_{m}$ and $x_{u}$.

Is the root now between $x_{l}$ and $x_{m}$ or between $x_{m}$ and $x_{u}$? Well, one can find the sign of $f(x_{l})f(x_{m})$, and if $f(x_{l})f(x_{m}) < 0$ then the new bracket is between $x_{l}$ and $x_{m}$, otherwise, it is between $x_{m}$ and $x_{u}$. So, you can see that you are literally halving the interval. As one repeats this process, the width of the interval $\left\lbrack x_{l},x_{u} \right\rbrack$ becomes smaller and smaller, and you can zero into the root of the equation $f(x) = 0$. The algorithm for the bisection method is given as follows.

Algorithm for the bisection method

The steps to apply the bisection method to find the root of the equation $f(x) = 0$ are

Choose $x_{l}$ and $x_{u}$ as two guesses for the root such that$f(x_{l})f(x_{u}) < 0$, or in other words, $f(x)$ changes sign between $x_{l}$ and $x_{u}$.

Estimate the root $x_{m}$ of the equation $f(x) = 0$ as the mid-point between $x_{l}$ and $x_{u}$ as

$$x_{m} = \frac{x_{l} + \ x_{u}}{2} \nonumber$$

Now check the following.

If $f(x_{l})f(x_{m}) < 0$, then the root lies between $x_{l}$ and $x_{m}$; then $x_{l} = x_{l}$ and $x_{u} = x_{m}$.

If $f(x_{l})f(x_{m}) > 0$, then the root lies between $x_{m}$ and $x_{u}$; then $x_{l} = x_{m}$ and $x_{u} = x_{u}$.

If $f(x_{l})f(x_{m}) = 0$; then the root is $x_{m}$. Stop the algorithm if this is true.

Find the new estimate of the root

$$x_{m} = \frac{x_{l} + \ x_{u}}{2} \nonumber$$

Find the absolute relative approximate error as

$$\left| \in_{a} \right| = \left| \frac{x_{m}^{\text{new}} - x_{m}^{\text{old}}}{x_{m}^{\text{new}}} \right|\ \times 100 \nonumber$$

where

$$x_{m}^{\text{new}} = \text{estimated root from the present iteration} \nonumber$$

$$x_{m}^{\text{old}}= \text{estimated root from the previous iteration} \nonumber$$

Compare the absolute relative approximate error $\left| \in_{a} \right|$ with the pre-specified relative error tolerance $\in_{s}$. If $\left| \in_{a} \right| > \in_{s}$, then go to Step 3, else stop the algorithm. Note one should also check whether the number of iterations is more than the maximum number of iterations allowed. If so, one needs to terminate the algorithm and notify the user about it.

Audiovisual Lectures

Title: Bisection Method - Algorithm

Summary: Learn the algorithm of the bisection method of solving nonlinear equations of the form $f(x) = 0$.

Lesson 3: Application of Bisection Method

Learning Objectives

After successful completion of this lesson, you should be able to:

1) apply the bisection method to solve for roots of a nonlinear equation.

Applications

In the previous lesson, you learned the theory of the bisection method of solving a nonlinear equation. In this lesson, we apply the algorithm of the bisection method to solve a nonlinear equation.

Example $\PageIndex{3.1}$

Use the bisection method to find the root of the nonlinear equation

$$x^{3} = 20 \nonumber$$

Use initial lower and upper guesses of $1$ and $4$, respectively.

Conduct three iterations to estimate the root of the equation.

Find the absolute relative approximate error at the end of each iteration.

Find the number of significant digits that are at least correct at the end of each iteration.

Solution

Rewrite the equation $x^3=20$ in the form $f(x) = 0$ that gives

$$f(x) = x^{3} - 20 = 0 \nonumber$$

Check if the function changes the sign between the two initial guesses, $x_{l}$ and $x_{u}$. The initial guesses are given as $x_{l} = 1$ and $x_{u} = 4$

$$\begin{split} f(x_{l}) &= f(1)\\ &= 1^{3} - 20\\ &= - 19\end{split} \nonumber$$

$$\begin{split} f(x_{u}) &= f(4)\\ &= 4^{3} - 20\\ &= 44\end{split} \nonumber$$

Hence

$$\begin{split} f(x_{l})f(x_{u}) &= f(1)f(4)\\ &= ( - 19)(44) < 0\end{split} \nonumber$$

This change in sign tells us that the initial bracket of $[1,4]$ given to us is valid.

Iteration 1

$$x_{l} = 1,\ x_{u} = 4 \nonumber$$

The estimate of the root is

$$\begin{split} x_{m} &= \frac{x_{l} + x_{u}}{2}\\ &= \frac{1 + 4}{2}\\ &= 2.5\end{split} \nonumber$$

Iteration 2

Find the value of the function at the midpoint from the previous iteration and use it to determine the new bracket.

$$\begin{split} f(x_{m}) &= f(2.5)\\ &= (2.5)^{3} - 20\\ &= - 4.375\end{split} \nonumber$$

$$\begin{split} f(x_{l})f(x_{m}) &= f(1)f(2.5)\\ &= ( - 19)( - 4.375) > 0\end{split} \nonumber$$

Since $f(x_{l})f(x_{m}) > 0$, the root does not lie between $x_{l}$ and $x_{m}$, but between $x_{m}$ and $x_{u}$, that is, $2.5$ and $4$.

$$x_{l} = 2.5,\ x_{u} = 4 \nonumber$$

The estimate of the root is

$$\begin{split} x_{m} &= \frac{x_{l} + x_{u}}{2}\\ &= \frac{2.5 + 4}{2}\\ &= 3.25\end{split} \nonumber$$

The absolute relative approximate error $\left| \varepsilon_{a} \right|$ at the end of Iteration 2 is

$$\begin{split} \left| \varepsilon_{a} \right| &= \left| \frac{x_{m}^{\text{new}} - x_{m}^{\text{old}}}{x_{m}^{\text{new}}} \right| \times 100\\ &= \left| \frac{3.25 - 2.5}{3.25} \right| \times 100\\ &= 23.1\%\end{split} \nonumber$$

None of the significant digits are at least correct in the estimated root of the equation because the absolute relative approximate error is greater than $5\%$.

Iteration 3

Find the value of the function at the midpoint from the previous iteration and use it to determine the new bracket.

$$\begin{split} f(x_{m}) &= f(3.25)\\ &= (3.25)^{3} - 20\\ &= 14.3281\end{split} \nonumber$$

$$\begin{split} f(x_{l})f(x_{m}) &= f(2.5)f(3.25)\\ &= ( - 4.375)(14.3281) < 0 \end{split} \nonumber$$

Since $f(x_{l})f(x_{m}) < 0$, the root does lie between $x_{l}$ and $x_{m}$, that is, $2.5$ and $3.25$.

$$x_{l} = 2.5,x_{u} = 3.25 \nonumber$$

The estimate of the root is

$$\begin{split} x_{m} &= \frac{x_{l} + x_{u}}{2}\\ &= \frac{2.5 + 3.25}{2}\\ &= 2.875\end{split} \nonumber$$

The absolute relative approximate error $\left| \varepsilon_{a} \right|$ at the end of Iteration 3 is

$$\begin{split} \left| \epsilon_{a} \right| &= \left| \frac{x_{m}^{\text{new}} - x_{m}^{\text{old}}}{x_{m}^{\text{new}}} \right| \times 100\\ &= \left| \frac{2.875 - 2.5}{2.875} \right| \times 100\\ &= 13.0\%\end{split} \nonumber$$

Still, none of the significant digits are at least correct in the estimated root of the equation as the absolute relative approximate error is greater than $5\%$.

Example $\PageIndex{3.2}$

You are working for ‘DOWN THE TOILET COMPANY’ that makes floats for ABC commodes. The floating ball has a specific gravity of $0.6$ and has a radius of $5.5\ \text{cm}$. You are asked to find the depth to which the ball is submerged when floating in the water.

The equation that gives the depth $x$ to which the ball is submerged underwater is given by

$$x^{3} - 0.165x^{2} + 3.993 \times 10^{- 4} = 0 \nonumber$$

Use the bisection method of finding roots of equations to find the depth $x$ to which the ball is submerged underwater. Conduct three iterations to estimate the root of the above equation. Find the absolute relative approximate error at the end of each iteration, and the number of significant digits at least correct at the end of each iteration.

Solution

From the physics of the problem, the ball would be submerged somewhere between $x = 0$ and $x = 2R$,

where

$$R = \text{radius of the ball,} \nonumber$$

that is

$$0 \leq x \leq 2R \nonumber$$

$$0 \leq x \leq 2(0.055) \nonumber$$ $$0 \leq x \leq 0.11 \nonumber$$

Figure $\PageIndex{3.1}$. Floating ball problem.

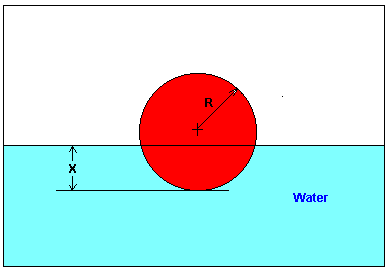
Let’s us assume

$$x_{l} = 0,\ x_{u} = 0.11 \nonumber$$

Check if the function changes sign between $x_{l}$ and $x_{u}$.

$$\begin{split} f(x_{l}) &= f(0) \\&= (0)^{3} - 0.165(0)^{2} + 3.993 \times 10^{- 4} \\&= 3.993 \times 10^{- 4} \end{split} \nonumber$$

$$\begin{split} f(x_{u}) &= f(0.11)\\ &= (0.11)^{3} - 0.165(0.11)^{2} + 3.993 \times 10^{- 4} \\&= - 2.662 \times 10^{- 4} \end{split} \nonumber$$

Hence

$$\begin{split} f(x_{l})f(x_{u}) &= f(0)f(0.11) \\&= (3.993 \times 10^{- 4})( - 2.662 \times 10^{- 4}) \\&< 0 \end{split} \nonumber$$

So, there is at least one root between $x_{l}$ and $x_{u}$, that is between $0$ and $0.11$.

Iteration 1

The estimate of the root is

$$\begin{split} x_{m} &= \frac{x_{l} + x_{u}}{2}\\ &= \frac{0 + 0.11}{2}\\ &= 0.055 \end{split} \nonumber$$

$$\begin{split} f\left(x_{m}\right)&=f(0.055)\\&=(0.055)^{3}-0.165(0.055)^{2}+3.993 \times 10^{-4}\\&=6.655 \times 10^{-5} \end{split} \nonumber$$

$$\begin{split} f(x_{l})f(x_{m}) &= f(0)f(0.055) \\&= \left( 3.993 \times 10^{- 4} \right)\left( 6.655 \times 10^{- 4} \right) \\&> 0 \end{split} \nonumber$$

Hence the root is bracketed between $x_{m}$ and $x_{u}$, that is, between $0.055$ and $0.11$. So, the lower and upper limit of the new bracket is

$$x_{l} = 0.055,\ x_{u} = 0.11 \nonumber$$

At this point, the absolute relative approximate error $\left| \epsilon_{a} \right|$ cannot be calculated as we do not have a previous approximation.

Iteration 2

The estimate of the root is

$$\begin{split} x_{m} &= \frac{x_{l} + x_{u}}{2}\\ &= \frac{0.055 + 0.11}{2}\\ &= 0.0825 \end{split} \nonumber$$

$$\begin{split} f(x_{m}) &= f(0.0825) \\&= (0.0825)^{3} - 0.165(0.0825)^{2} + 3.993 \times \text{1}\text{0}^{- 4}\\ &= - 1.622 \times \text{1}\text{0}^{- 4}\end{split} \nonumber$$

$$\begin{split} f\left( x_{l} \right)f\left( x_{m} \right) &= f\left( 0.055 \right)f\left( 0.0825 \right) \\&= \left( 6.655 \times 10^{- 5} \right) \times \left( - 1.622 \times 10^{- 4} \right) \\&<0 \end{split} \nonumber$$

Hence, the root is bracketed between $x_{l}$ and $x_{m}$, that is, between $0.055$ and $0.0825$. So, the lower and upper limit of the new bracket is

$$x_{l} = 0.055,\ x_{u} = 0.0825 \nonumber$$

The absolute relative approximate error $\left| \epsilon_{a} \right|$ at the end of Iteration 2 is

$$\begin{split} \left| \epsilon_{a} \right| &= \left| \frac{x_{m}^{\text{new}} - x_{m}^{\text{old}}}{x_{m}^{\text{new}}} \right| \times 100\\ &= \left| \frac{0.0825 - 0.055}{0.0825} \right| \times 100\\ &= 33.33\% \end{split} \nonumber$$

None of the significant digits are at least correct in the estimated root of $x_{m} = 0.0825$ because the absolute relative approximate error is greater than $5\%$.

Iteration 3

$$\begin{split} x_{m} &= \frac{x_{l} + x_{u}}{2}\\ &= \frac{0.055 + 0.0825}{2}\\ &= 0.06875 \end{split} \nonumber$$

$$\begin{split} f\left( x_{m} \right) &= f(0.06875) \\&= (0.06875)^{3} - 0.165(0.06875)^{2} + 3.993 \times {1}{0}^{- 4}\\&= - 5.563 \times {1}{0}^{- 5} \end{split} \nonumber$$

$$\begin{split} f(x_{l})f(x_{m}) &= f(0.055)f(0.06875) \\&= (6.655 \times 10^{5}) \times ( - \text{5.563} \times 10^{- 5}) \\&< 0 \end{split} \nonumber$$

Hence, the root is bracketed between $x_{l}$ and $x_{m}$, that is, between $0.055$ and $0.06875$. So the lower and upper limit of the new bracket is

$$x_{l} = 0.055,\ x_{u} = 0.06875 \nonumber$$

The absolute relative approximate error $\left| \epsilon_{a} \right|$ at the ends of Iteration 3 is

$$\begin{split} \left| \epsilon_{a} \right| &= \left| \frac{x_{m}^{\text{new}} - x_{m}^{\text{old}}}{x_{m}^{\text{new}}} \right| \times 100\\ &= \left| \frac{0.06875 - 0.0825}{0.06875} \right| \times 100\\ &= 20\% \end{split} \nonumber$$

Still, none of the significant digits are at least correct in the estimated root of the equation as the absolute relative approximate error is greater than $5\%$.

Seven more iterations were conducted, and these iterations are shown in Table $\PageIndex{3.1}$.

Table $\PageIndex{3.1}$. Root of $f(x) = 0$ as function of number of iterations for bisection method.

Iteration	$x_{l}$	$x_{u}$	$x_{m}$	$\left| \epsilon_{a} \right|\%$	$f(x_{m})$
$1$	$0.00000$	$0.11$	$0.055$	$---$	$6.655 \times 10^{- 5}$
$2$	$0.055$	$0.11$	$0.0825$	$33.33$	$- 1.622 \times 10^{- 4}$
$3$	$0.055$	$0.0825$	$0.06875$	$20.00$	$- 5.563 \times 10^{- 5}$
$4$	$0.055$	$0.06875$	$0.06188$	$11.11$	$4.484 \times 10^{- 6}$
$5$	$0.06188$	$0.06875$	$0.06531$	$5.263$	$- 2.593 \times 10^{- 5}$
$6$	$0.06188$	$0.06531$	$0.06359$	$2.702$	$- 1.0804 \times 10^{- 5}$
$7$	$0.06188$	$0.06359$	$0.06273$	$1.370$	$- 3.176 \times 10^{- 6}$
$8$	$0.06188$	$0.06273$	$0.0623$	$0.6897$	$6.497 \times 10^{- 7}$
$9$	$0.0623$	$0.06273$	$0.06252$	$0.3436$	$- 1.265 \times 10^{- 6}$
$10$	$0.0623$	$0.06252$	$0.06241$	$0.1721$	$- 3.0768 \times 10^{- 7}$

At the end of the $10^{\text{th}}$ iteration,

$$\left| \epsilon_{a} \right| = 0.1721\% \nonumber$$

Hence the number of significant digits at least correct is given by the largest value of $m$ for which

$$\left| \epsilon_{a} \right| \leq 0.5 \times 10^{2 - m} \nonumber$$

$$0.1721 \leq 0.5 \times 10^{2 - m} \nonumber$$

$$0.3442 \leq 10^{2 - m} \nonumber$$

$$\log(0.3442) \leq 2 - m \nonumber$$

$$m \leq 2 - \log(0.3442) = 2.463 \nonumber$$

So

$$m = 2 \nonumber$$

The number of significant digits at least correct in the estimated root of $0.06241$ at the end of the $10^{\text{th}}$ iteration is $2$.

Lesson 4: Advantages and Pitfalls of Bisection Method

Learning Objectives

After successful completion of this lesson, you should be able to

1) enumerate the advantages of the bisection method and the reasoning behind them.

2) list the drawbacks of the bisection method and the reason behind them.

Advantages of the bisection method

a) The bisection method is always convergent. Since the technique brackets the root, the procedure is guaranteed to converge.

b) As iterations are conducted, the interval gets halved. So, one can guarantee the error in the solution of the equation.

Drawbacks of bisection method

a) The convergence of the bisection method is slow as it is based on halving the interval.

b) If one of the initial guesses is closer to the root, it will take a larger number of iterations to reach the root.

c) If a function $f(x)$ is such that it just touches the x-axis (Figure $\PageIndex{4.1}$) such as

$$f(x) = x^{2} = 0 \nonumber$$

it will be unable to find the lower guess, $x_{l}$, and upper guess, $x_{u}$, such that

$$f(x_{l})f(x_{u}) < 0 \nonumber$$

d) For functions $f(x)$ where there is a singularity, and it reverses the sign at the singularity, the bisection method may converge on the singularity (Figure $\PageIndex{4.2}$). An example includes

$$f(x) = \frac{1}{x} \nonumber$$

where $x_{l} = - 2$, $x_{u} = 3$ are valid initial guesses which satisfy

$$f(x_{l})f(x_{u}) < 0 \nonumber$$

However, the function is not continuous, and the theorem that a root exists is also not applicable.

Figure $\PageIndex{4.1}$. The equation $f(x) = x^{2} = 0$ has a single root at $x = 0$ that cannot be bracketed.

Figure $\PageIndex{4.2}$. The equation $\displaystyle f\left( x \right) = \frac{1}{x} = 0$ has no root but changes sign.

Audiovisual Lecture

Title: Bisection Method: Advantages and Drawbacks

Summary: This video discusses the advantages and drawbacks of the bisection method - a numerical method to find roots of a nonlinear equation.

Multiple Choice Test

(1). The bisection method of finding roots of nonlinear equations falls under the category of a(n) _________ method.

(A) open

(B) bracketing

(C) random

(D) graphical

(2). If $f(a)f\left( b \right) < 0$ for a real continuous function $f\left( x \right)$, then in the domain of $\left\lbrack a,b \right\rbrack$ for $f\left( x \right) = 0$, there is (are)

(A) one root

(B) an undeterminable number of roots

(C) no root

(D) at least one root

(3). Assuming an initial bracket of $\left\lbrack 1,5 \right\rbrack$, the second (at the end of 2 iterations) iterative value of the root of $te^{- t} - 0.3 = 0$ using the bisection method is

(A) $0$

(B) $1.5$

(C) $2$

(D) $3$

(4). To find the root of $f(x) = 0$, a scientist is using the bisection method. At the beginning of an iteration, the lower and upper guesses of the root are $x_{l}$ and $x_{u}$. At the end of the iteration, the absolute relative approximate error in the estimated value of the root would be

(A) $\displaystyle \left| \frac{x_{u}}{x_{u} + x_{l}} \right|$

(B) $\displaystyle \left| \frac{x_{l}}{x_{u} + x_{l}} \right|$

(C) $\displaystyle \left| \frac{x_{u} - x_{l}}{x_{u} + x_{l}} \right|$

(D) $\displaystyle \left| \frac{x_{u} + x_{l}}{x_{u} - x_{l}} \right|$

(5). For an equation like $x^{2} = 0$, a root exists at $x = 0$. The bisection method cannot be adopted to solve this equation in spite of the root existing at $x = 0$ because the function $f\left( x \right) = x^{2}$

(A) is a polynomial

(B) has repeated zeros at $x = 0$

(C) is always non-negative

(D) has a slope equal to zero at $x = 0$

(6). The ideal gas law is given by

$$pv = RT \nonumber$$

where $p$ is the pressure, $v$ is the specific volume, $R$ is the universal gas constant, and $T$ is the absolute temperature. This equation is only accurate for a limited range of pressure and temperature. Vander Waals came up with an equation that was accurate for larger ranges of pressure and temperature given by

$$\displaystyle \left( p + \frac{a}{v^{2}} \right)\left( v - b \right) = RT \nonumber$$

where $a$ and $b$ are empirical constants dependent on a particular gas. Given the value of $R = 0.08$, $a = 3.592$, $b = 0.04267$, $p = 10$ and $T = 300$ (assume all units are consistent), one is going to find the specific volume, $v$, for the above values. Without finding the solution from the Vander Waals equation, what would be a good initial guess for $v$?

(A) $0$

(B) $1.2$

(C) $2.4$

(D) $3.6$

For complete solution, go to

http://nm.mathforcollege.com/mcquizzes/03nle/quiz_03nle_bisection_solution.pdf

Problem Set

(1). Find the estimate of the root of $x^{2} - 4 = 0$ by using the bisection method. Use initial guesses of $1.7$ and $2.4$. Conduct three iterations, and calculate the approximate error, true error, absolute relative approximate error, and absolute relative true error at the end of each iteration.

Answer

Iteration #	Root Estimate	Approx Error	True Error	Abs Rel Approx Error	Abs Rel True Error
$1$	$2.05$	$---$	$-0.05$	$---$	$2.5\%$
$2$	$1.875$	$-0.175$	$0.125$	$9.33\%$	$6.25\%$
$3$	$1.9625$	$0.0875$	$0.0375$	$4.45\%$	$1.875\%$

(2). You are working for DOWN THE TOILET COMPANY that makes floats for ABC commodes. The ball has a specific gravity of 0.6 and has a radius of 5.5 cm. You are asked to find the depth to which the ball will get submerged when floating in the water.

The equation that gives the depth $x$ (unit of $x$ is meters) to which the ball is submerged under water is given by

$$x^{3} - 0.165x^{2} + 3.993 \times 10^{- 4} = 0 \nonumber$$

Solving it exactly would require some effort. However, using numerical techniques such as the bisection method, we can solve this equation and any other equation of the form $f(x) = 0$. Solve the above equation by the bisection method and do the following. Use initial guesses of $x = 0$ and $x = 0.11$.

a) Conduct three iterations.

b) Calculate the absolute relative approximate error at the end of each step.

c) Find the number of significant digits at least correct at the end of each iteration.

d) How can you use the knowledge of the physics of the problem to develop initial guesses for the bisection method?

Answer

$a)\ 0.055, 0.0825, 0.06875$

$b)\ n/a, 33.333\%, 20.00\%$

$c)\ n/a, 0, 0$

$d)$ Since the diameter is $0.11\ \text{m}$, initial guesses of $0$ and $0.11$ are reasonable starting values

(3). The velocity of a body is given by the following equation

$$v(t) = te^{- t} + \frac{1}{t} \nonumber$$

where

$t$ is given in seconds and $v$ is given in m/s.

Find the time when the velocity of the body will be $0.35\ \text{m/s}$. Use bisection method and conduct three iterations. Use initial bracketing guess of $[1,8]$. Show all steps in calculating the estimated root, absolute relative approximate error and the velocity of the body for each iteration. Also, tabulate your answers as iteration number, estimated root, absolute relative approximate error, and velocity of the body.

Answer

Iteration	Estimated Root	$|\epsilon_a|\%$	$v(t)\ (\text{m/s})$
$1$	$4.500$	$-$	$0.27221$
$2$	$2.750$	$63.663$	$0.53944$
$3$	$3.6250$	$24.138$	$0.37247$

(4). Enumerate the drawbacks of the bisection method of solving nonlinear equations.

(5). The velocity of a body is given by

$$v = 5e^{- t} + 4 + \sin(t), \nonumber$$

where

$v$ is given in m/s,

$t$ is given in s.

Derive the nonlinear equation that you will need to solve to find when the acceleration of the body would be $1.54 \ \text{m/s}^{2}$. Find the solution of the equation by using three iterations of the bisection method.

Answer

The equation has no real roots. Note the question asks when acceleration is $1.54 \ \text{m/s}^{2}$

(6). To solve the equation $f(x) = 0$, an engineer is using the bisection method. He starts with an initial valid bracket of $[2, 7]$. Find the maximum possible absolute true error in his estimate of the root at the end of two iterations. Show your reasoning clearly for your answer.

Answer

$1.25$

(7). Estimate the next guess for the root of $x^{2} - 16 = 0$ by using a modified bisection method as explained below. The initial bracket of $[1,8]$ is found as a valid bracket. In the case of bisection method, the root estimated at the end of the first iteration is the midpoint between $1$ and $8$. Instead, in the modified bisection method, the root estimated at the end of the first iteration would be the point where the straight line drawn from the function at $x = 1$ to the function at $x = 8$ crosses the $x$ -axis. What is this estimate of the root?

Answer

$2.667$