22.1: Structure of a Finite Field

Recall that a field $F$ has characteristic $p$ if $p$ is the smallest positive integer such that for every nonzero element $\alpha$ in $F\text{,}$ we have $p \alpha = 0\text{.}$ If no such integer exists, then $F$ has characteristic $0\text{.}$ From Theorem $16.19$ we know that $p$ must be prime. Suppose that $F$ is a finite field with $n$ elements. Then $n \alpha = 0$ for all $\alpha$ in $F\text{.}$ Consequently, the characteristic of $F$ must be $p\text{,}$ where $p$ is a prime dividing $n\text{.}$ This discussion is summarized in the following proposition.

Proposition $22.1$.

If $F$ is a finite field, then the characteristic of $F$ is $p\text{,}$ where $p$ is prime.

 

Throughout this chapter we will assume that $p$ is a prime number unless otherwise stated.

Proposition $22.2$.

If $F$ is a finite field of characteristic $p\text{,}$ then the order of $F$ is $p^n$ for some $n \in {\mathbb N}\text{.}$

Proof

Let $\phi : {\mathbb Z} \rightarrow F$ be the ring homomorphism defined by $\phi(n) = n \cdot 1\text{.}$ Since the characteristic of $F$ is $p\text{,}$ the kernel of $\phi$ must be $p {\mathbb Z}$ and the image of $\phi$ must be a subfield of $F$ isomorphic to ${\mathbb Z}_p\text{.}$ We will denote this subfield by $K\text{.}$ Since $F$ is a finite field, it must be a finite extension of $K$ and, therefore, an algebraic extension of $K\text{.}$ Suppose that $[F : K] = n$ is the dimension of $F\text{,}$ where $F$ is a $K$ vector space. There must exist elements $\alpha_1, \ldots, \alpha_n \in F$ such that any element $\alpha$ in $F$ can be written uniquely in the form

$$\alpha = a_1 \alpha_1 + \cdots + a_n \alpha_n\text{,} \nonumber$$

where the $a_i$'s are in $K\text{.}$ Since there are $p$ elements in $K\text{,}$ there are $p^n$ possible linear combinations of the $\alpha_i$'s. Therefore, the order of $F$ must be $p^n\text{.}$

Lemma $22.3$. Freshman's Dream

Let $p$ be prime and $D$ be an integral domain of characteristic $p\text{.}$ Then

$$a^{p^n} + b^{p^n} = (a + b)^{p^n} \nonumber$$

for all positive integers $n\text{.}$

Proof

We will prove this lemma using mathematical induction on $n\text{.}$ We can use the binomial formula (see Chapter 2, Example $2.4$) to verify the case for $n = 1\text{;}$ that is,

$$(a + b)^p = \sum_{k = 0}^{p} \binom{p}{k} a^k b^{p - k}\text{.} \nonumber$$

If $0 \lt k \lt p\text{,}$ then

$$\binom{p}{k} = \frac{p!}{k!(p - k)!} \nonumber$$

must be divisible by $p\text{,}$ since $p$ cannot divide $k!(p - k)!\text{.}$ Note that $D$ is an integral domain of characteristic $p\text{,}$ so all but the first and last terms in the sum must be zero. Therefore, $(a + b)^p = a^p + b^p\text{.}$

Now suppose that the result holds for all $k\text{,}$ where $1 \leq k \leq n\text{.}$ By the induction hypothesis,

$$(a + b)^{p^{n + 1}} = ((a + b)^p)^{p^{n}} = (a^p + b^p)^{p^{n}} = (a^p)^{p^{n}} + (b^p)^{p^{n}} = a^{p^{n + 1}} + b^{p^{n + 1}}\text{.} \nonumber$$

Therefore, the lemma is true for $n + 1$ and the proof is complete.

Let $F$ be a field. A polynomial $f(x) \in F[x]$ of degree $n$ is separable if it has $n$ distinct roots in the splitting field of $f(x)\text{;}$ that is, $f(x)$ is separable when it factors into distinct linear factors over the splitting field of $f\text{.}$ An extension $E$ of $F$ is a separable extension of $F$ if every element in $E$ is the root of a separable polynomial in $F[x]\text{.}$

Example $22.4$.

The polynomial $x^2 - 2$ is separable over ${\mathbb Q}$ since it factors as $(x - \sqrt{2}\, )(x + \sqrt{2}\, )\text{.}$ In fact, ${\mathbb Q}(\sqrt{2}\, )$ is a separable extension of ${\mathbb Q}\text{.}$ Let $\alpha = a + b \sqrt{2}$ be any element in ${\mathbb Q}(\sqrt{2}\, )\text{.}$ If $b = 0\text{,}$ then

Solution

$\alpha$ is a root of $x - a\text{.}$ If $b \neq 0\text{,}$ then $\alpha$ is the root of the separable polynomial

$$x^2 - 2 a x + a^2 - 2 b^2 = (x - (a + b \sqrt{2}\, ))(x - (a - b \sqrt{2}\, ))\text{.} \nonumber$$

Fortunately, we have an easy test to determine the separability of any polynomial. Let

$$f(x) = a_0 + a_1 x + \cdots + a_n x^n \nonumber$$

be any polynomial in $F[x]\text{.}$ Define the derivative of $f(x)$ to be

$$f'(x) = a_1 + 2 a_2 x + \cdots + n a_n x^{n - 1}\text{.} \nonumber$$

Lemma $22.5$.

Let $F$ be a field and $f(x) \in F[x]\text{.}$ Then $f(x)$ is separable if and only if $f(x)$ and $f'(x)$ are relatively prime.

Proof

Let $f(x)$ be separable. Then $f(x)$ factors over some extension field of $F$ as $f(x) = (x - \alpha_1) (x - \alpha_2) \cdots (x - \alpha_n)\text{,}$ where $\alpha_i \neq \alpha_j$ for $i \neq j\text{.}$ Taking the derivative of $f(x)\text{,}$ we see that

$$\begin{align*} f'(x) & = (x - \alpha_2) \cdots (x - \alpha_n)\\ & + (x - \alpha_1) (x - \alpha_3) \cdots (x - \alpha_n)\\ & + \cdots + (x - \alpha_1) \cdots (x - \alpha_{n - 1})\text{.} \end{align*}$$

Hence, $f(x)$ and $f'(x)$ can have no common factors.

To prove the converse, we will show that the contrapositive of the statement is true. Suppose that $f(x) = (x - \alpha)^k g(x)\text{,}$ where $k \gt 1\text{.}$ Differentiating, we have

$$f'(x) = k ( x - \alpha)^{k-1} g(x) + (x- \alpha)^k g'(x)\text{.} \nonumber$$

Therefore, $f(x)$ and $f'(x)$ have a common factor.

Theorem $22.6$.

For every prime $p$ and every positive integer $n\text{,}$ there exists a finite field $F$ with $p^n$ elements. Furthermore, any field of order $p^n$ is isomorphic to the splitting field of $x^{p^n} -x$ over ${\mathbb Z}_p\text{.}$

Proof

Let $f(x) = x^{p^n} - x$ and let $F$ be the splitting field of $f(x)\text{.}$ Then by Lemma 22.5, $f(x)$ has $p^n$ distinct zeros in $F\text{,}$ since $f'(x) = p^n x^{p^n - 1} - 1 = -1$ is relatively prime to $f(x)\text{.}$ We claim that the roots of $f(x)$ form a subfield of $F\text{.}$ Certainly 0 and 1 are zeros of $f(x)\text{.}$ If $\alpha$ and $\beta$ are zeros of $f(x)\text{,}$ then $\alpha + \beta$ and $\alpha \beta$ are also zeros of $f(x)\text{,}$ since $\alpha^{p^n} + \beta^{p^n} = (\alpha + \beta)^{p^n}$ and $\alpha^{p^n} \beta^{p^n} = (\alpha \beta)^{p^n}\text{.}$ We also need to show that the additive inverse and the multiplicative inverse of each root of $f(x)$ are roots of $f(x)\text{.}$ For any zero $\alpha$ of $f(x)\text{,}$ we know that $-\alpha$ is also a zero of $f(x)\text{,}$ since

$$f(-\alpha) = (-\alpha)^{p^n} - (-\alpha) = -\alpha^{p^n} + \alpha = -(\alpha^{p^n} - \alpha) = 0\text{,} \nonumber$$

provided $p$ is odd. If $p = 2\text{,}$ then

$$f(-\alpha) = (-\alpha)^{2^n} - (-\alpha) = \alpha + \alpha = 0\text{.} \nonumber$$

If $\alpha \neq 0\text{,}$ then $(\alpha^{-1})^{p^n} = (\alpha^{p^n})^{-1} = \alpha^{-1}\text{.}$ Since the zeros of $f(x)$ form a subfield of $F$ and $f(x)$ splits in this subfield, the subfield must be all of $F\text{.}$

Let $E$ be any other field of order $p^n\text{.}$ To show that $E$ is isomorphic to $F\text{,}$ we must show that every element in $E$ is a root of $f(x)\text{.}$ Certainly 0 is a root of $f(x)\text{.}$ Let $\alpha$ be a nonzero element of $E\text{.}$ The order of the multiplicative group of nonzero elements of $E$ is $p^n-1\text{;}$ hence, $\alpha^{p^n-1} =1$ or $\alpha^{p^n} -\alpha = 0\text{.}$ Since $E$ contains $p^n$ elements, $E$ must be a splitting field of $f(x)\text{;}$ however, by Corollary 21.36, the splitting field of any polynomial is unique up to isomorphism.

The unique finite field with $p^n$ elements is called the Galois field of order $p^n\text{.}$ We will denote this field by $\gf(p^n)\text{.}$

Theorem $22.7$.

Every subfield of the Galois field $\gf(p^n)$ has $p^m$ elements, where $m$ divides $n\text{.}$ Conversely, if $m \mid n$ for $m \gt 0\text{,}$ then there exists a unique subfield of $\gf(p^n)$ isomorphic to $\gf(p^m)\text{.}$

Proof

Let $F$ be a subfield of $E = \gf(p^n)\text{.}$ Then $F$ must be a field extension of $K$ that contains $p^m$ elements, where $K$ is isomorphic to ${\mathbb Z}_p\text{.}$ Then $m \mid n\text{,}$ since $[E:K] = [E:F][F:K]\text{.}$

To prove the converse, suppose that $m \mid n$ for some $m \gt 0\text{.}$ Then $p^m -1$ divides $p^n -1\text{.}$ Consequently, $x^{p^m -1} - 1$ divides $x^{p^n -1} -1\text{.}$ Therefore, $x^{p^m} - x$ must divide $x^{p^n} - x\text{,}$ and every zero of $x^{p^m} - x$ is also a zero of $x^{p^n} - x\text{.}$ Thus, $\gf(p^n)$ contains, as a subfield, a splitting field of $x^{p^m} - x\text{,}$ which must be isomorphic to $\gf(p^m)\text{.}$

Example $22.8$.

The lattice of subfields of $\gf(p^{24})$ is given in Figure $22.9$.

Solution

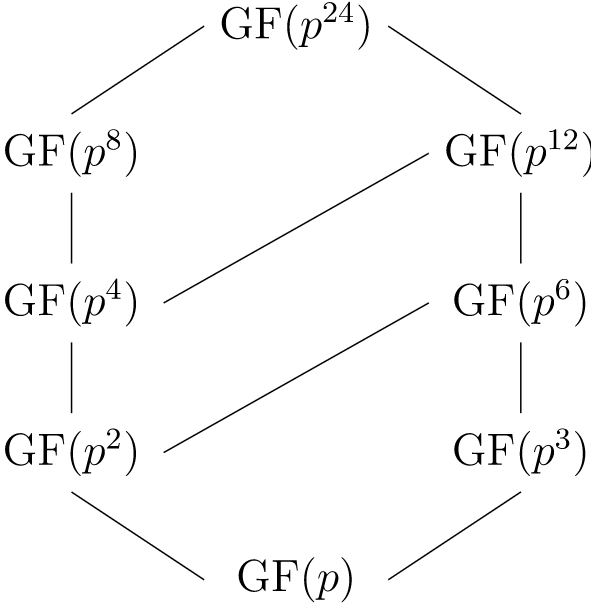
$Figure \text { } 22.9.$ Subfields of $\gf(p^{24})$

With each field $F$ we have a multiplicative group of nonzero elements of $F$ which we will denote by $F^*\text{.}$ The multiplicative group of any finite field is cyclic. This result follows from the more general result that we will prove in the next theorem.

Theorem $22.10$.

If $G$ is a finite subgroup of $F^\ast\text{,}$ the multiplicative group of nonzero elements of a field $F\text{,}$ then $G$ is cyclic.

Proof

Let $G$ be a finite subgroup of $F^\ast$ of order $n\text{.}$ By the Fundamental Theorem of Finite Abelian Groups (Theorem $13.4$),

$$G \cong {\mathbb Z}_{p_1^{e_1}} \times \cdots \times {\mathbb Z}_{p_k^{e_k}}\text{,} \nonumber$$

where $n = p_1^{e_1} \cdots p_k^{e_k}$ and the $p_1, \ldots, p_k$ are (not necessarily distinct) primes. Let $m$ be the least common multiple of $p_1^{e_1}, \ldots, p_k^{e_k}\text{.}$ Then $G$ contains an element of order $m\text{.}$ Since every $\alpha$ in $G$ satisfies $x^r - 1$ for some $r$ dividing $m\text{,}$ $\alpha$ must also be a root of $x^m - 1\text{.}$ Since $x^m -1$ has at most $m$ roots in $F\text{,}$ $n \leq m\text{.}$ On the other hand, we know that $m \leq |G|\text{;}$ therefore, $m = n\text{.}$ Thus, $G$ contains an element of order $n$ and must be cyclic.

Corollary $22.11$.

The multiplicative group of all nonzero elements of a finite field is cyclic.

Corollary $22.12$.

Every finite extension $E$ of a finite field $F$ is a simple extension of $F\text{.}$

Proof

Let $\alpha$ be a generator for the cyclic group $E^{\ast}$ of nonzero elements of $E\text{.}$ Then $E = F( \alpha )\text{.}$

Example $22.13$.

The finite field $\gf(2^4)$ is isomorphic to the field ${\mathbb Z}_2/ \langle 1 + x + x^4 \rangle\text{.}$ Therefore, the elements of $\gf(2^4)$ can be taken to be

$$\{ a_0 + a_1 \alpha + a_2 \alpha^2 + a_3 \alpha^3 : a_i \in {\mathbb Z}_2 \text{ and } 1 + \alpha + \alpha^4 = 0 \}\text{.} \nonumber$$

Solution

Remembering that $1 + \alpha +\alpha^4 = 0\text{,}$ we add and multiply elements of $\gf(2^4)$ exactly as we add and multiply polynomials. The multiplicative group of $\gf(2^4)$ is isomorphic to ${\mathbb Z}_{15}$ with generator $\alpha\text{:}$

$$\begin{align*} & \alpha^1 = \alpha & & \alpha^6 = \alpha^2 + \alpha^3 & & \alpha^{11} = \alpha + \alpha^2 + \alpha^3 &\\ & \alpha^2 = \alpha^2 & & \alpha^7 = 1 + \alpha + \alpha^3 & & \alpha^{12} = 1 + \alpha + \alpha^2 + \alpha^3 &\\ & \alpha^3 = \alpha^3 & & \alpha^8 = 1 + \alpha^2 & & \alpha^{13} = 1 + \alpha^2 + \alpha^3 &\\ & \alpha^4 = 1 + \alpha & & \alpha^9 = \alpha + \alpha^3 & & \alpha^{14} = 1 + \alpha^3 &\\ &\alpha^5 = \alpha + \alpha^2 & & \alpha^{10} = 1 + \alpha + \alpha^2 & & \alpha^{15} = 1. & \end{align*}$$