2.8: Roots and Factorization of Polynomials

Last updated
Save as PDF

Page ID: 40906

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

In this section we will use some of the skills we have seen in previous sections in order to find all the roots of a polynomial function (both real and complex) and also factor the polynomial as the product of prime factors with integer coefficients.
Example
Find all real and complex roots for the given equation. Express the given polynomial as the product of prime factors with integer coefficients.
$2 x^{3}-3 x^{2}+2 x-8=0$
First we'll graph the polynomial to see if we can find any real roots from the graph:
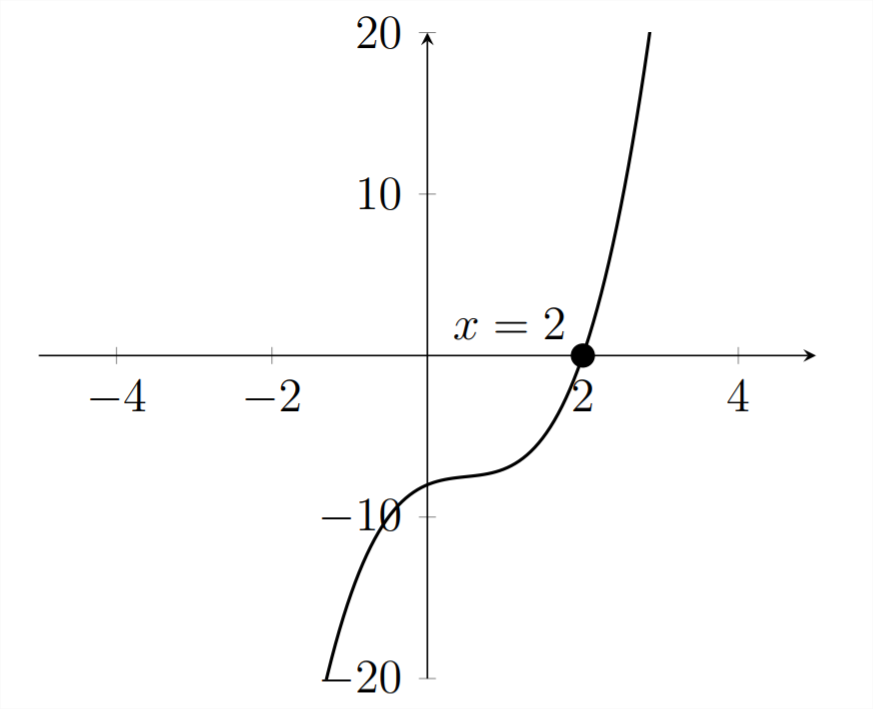
$clipboard_e8eb093603e45a425a1b025501b56e570.png$
We can see that there is a root at $x=2 .$ This means that the polynomial will have a factor of $(x-2) .$ We can use Synthetic Division to find any other factors. Because $x=2$ is a root, we should get a zero remainder:
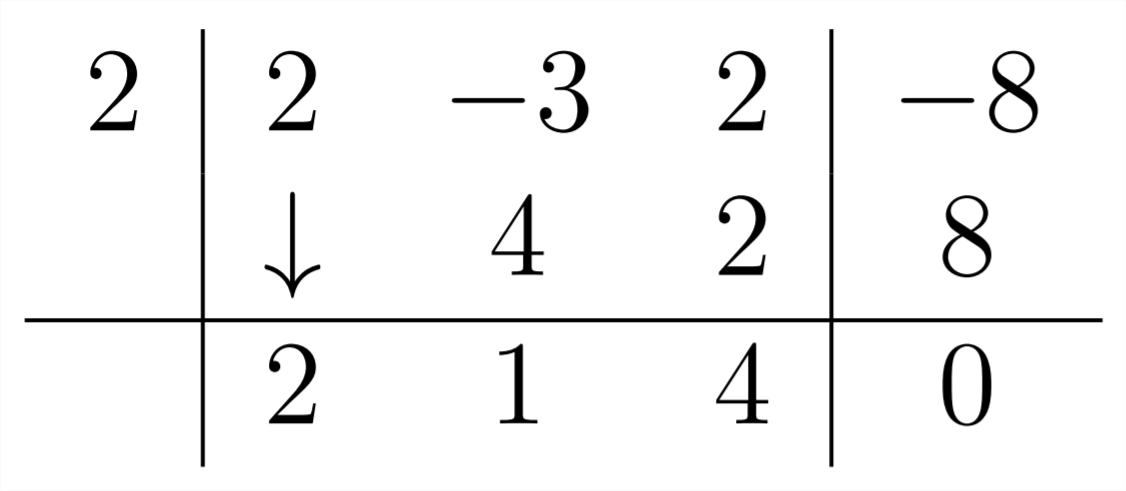
$clipboard_ebc1dd0fab74440b974eb51f8e6f64f73.png$
So, now we know that $2 x^{3}-3 x^{2}+2 x-8=(x-2)\left(2 x^{2}+x+4\right)$. To finish the problem, we can set each factor equal to zero and find the roots:
\[
\begin{array}{c}
2 x^{3}-3^{2}+2 x-8=0 \\
(x-2)\left(2 x^{2}+x+4\right)=0 \\
x-2=0 \quad 2 x^{2}+x+4=0 \\
x=2 \quad x \approx-0.25 \pm 1.392 i
\end{array}
\]
Let's look at an example that has more than one real root:

Example
Find all real and complex roots for the given equation. Express the given polynomial as the product of prime factors with integer coefficients.
\[
3 x^{4}+5 x^{3}-45 x^{2}+19 x-30=0
\]
First we'll graph the polynomial to see if we can find any real roots from the graph:
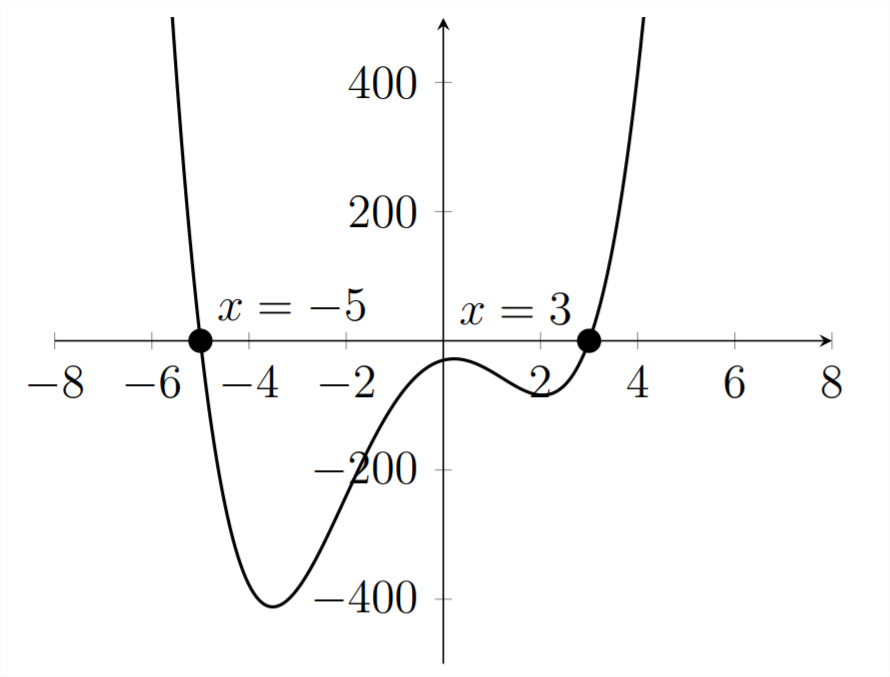
$clipboard_eee512b6b735161ef5a50aefa9a5d9385.png$

We can see roots at $x=-5,3,$ which means that $(x+5)$ and $(x-3)$ are both factors of this polynomial. We'll need to divide by both of these factors to break down the polynomial. First, we divide by $(x-3):$
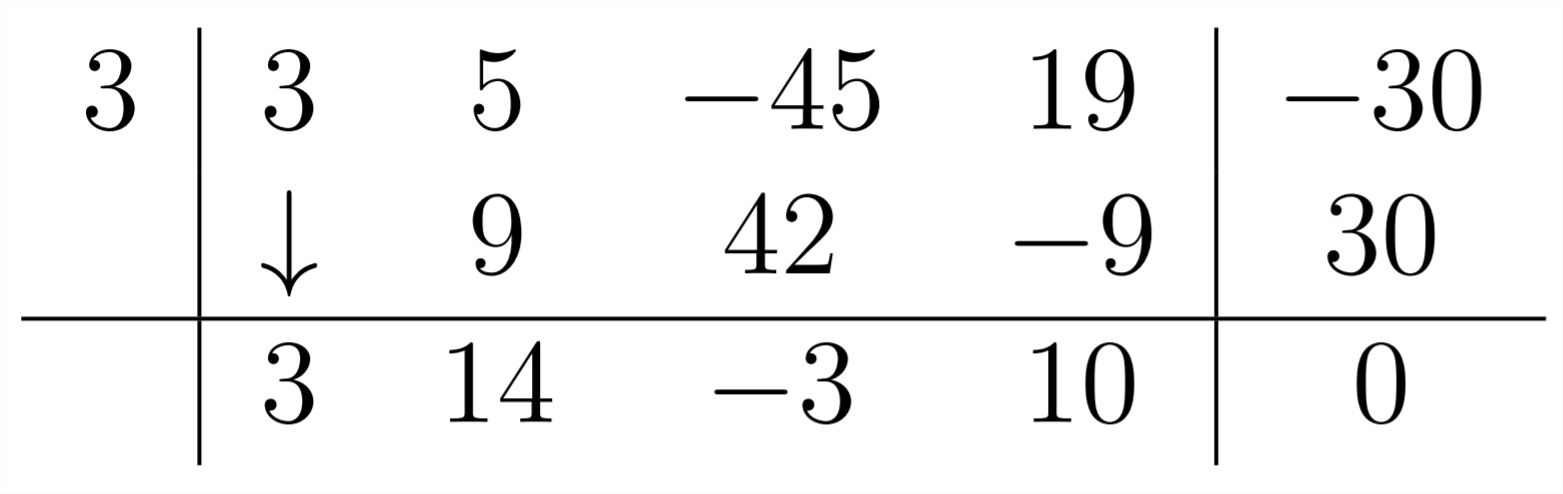
$clipboard_e306431e9058940377703f7a9e153612e.png$
And then by $(x+5):$
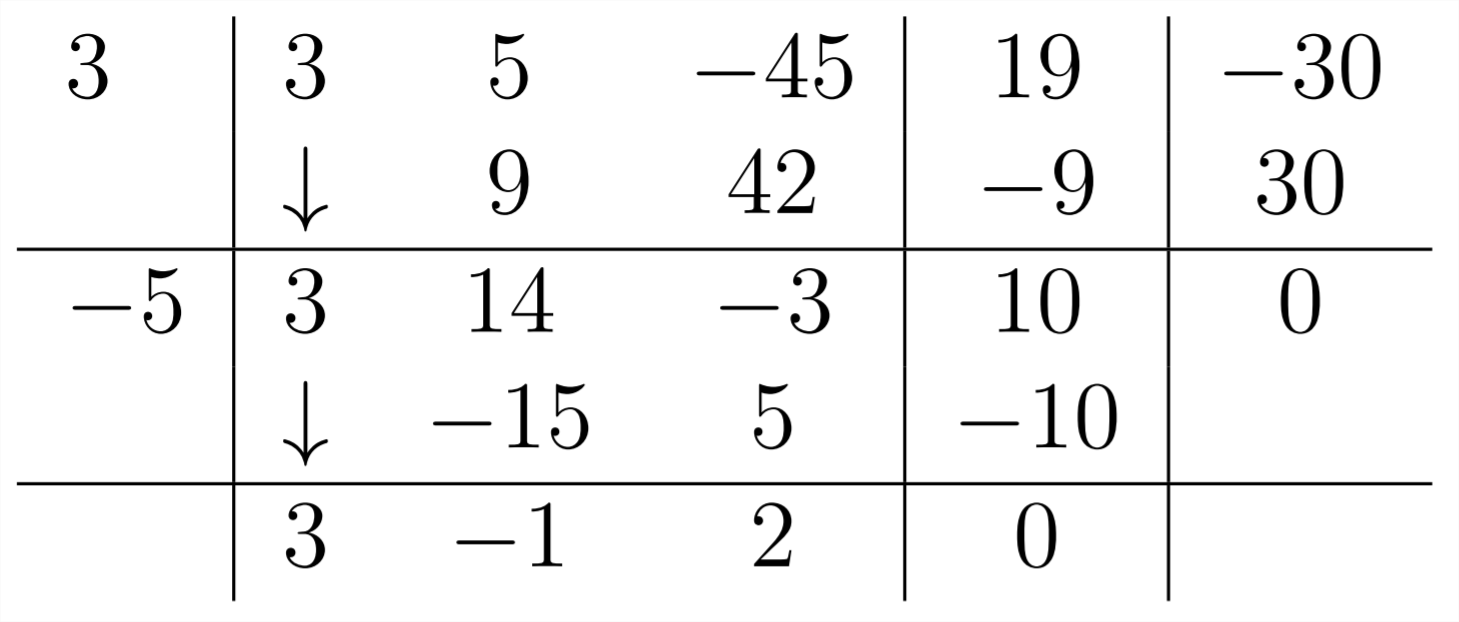
$clipboard_e82ce09925019a9cdc071947221c09896.png$
Now we know that $3 x^{4}+5 x^{3}-45 x^{2}+19 x-30=(x+5)(x-3)\left(3 x^{2}-x+2\right)$ and
so, to finish the problem:
\begin{array}{c}
3 x^{4}+5 x^{3}-45 x^{2}+19 x-30=0 \\
(x+5)(x-3)\left(3 x^{2}-x+2\right)=0 \\
x+5=0 \quad x-3=0 \quad 3 x^{2}-x+2=0 \\
x=-5 \quad x=3 \quad x \approx \frac{1}{6} \pm 0.799 i
\end{array}

Next, let's look at an example where there is a root that is not a whole number:

Example

Find all real and complex roots for the given equation. Express the given polynomial as the product of prime factors with integer coefficients.
$3 x^{3}+x^{2}+17 x+28=0$

First we'll graph the polynomial to see if we can find any real roots from the graph:
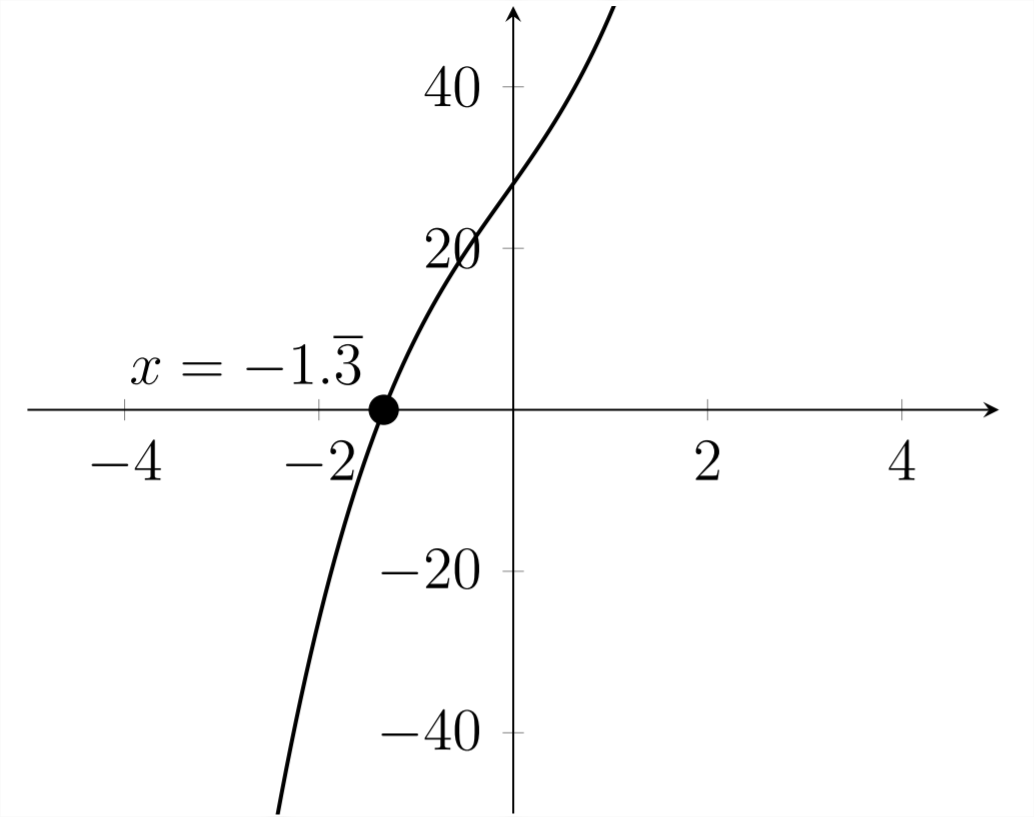
$clipboard_e7190cc22ea9cf7bdc414452c4a7454d4.png$
We can see in the graph that this polynomial has a root at $x=-\frac{4}{3}$. That means that the polynomial must have a factor of $3 x+4 .$ We can use Synthetic Division to find the other factor for this polynomial. Because we know that $x=-\frac{4}{3}$ is a root, we should get a zero remainder:
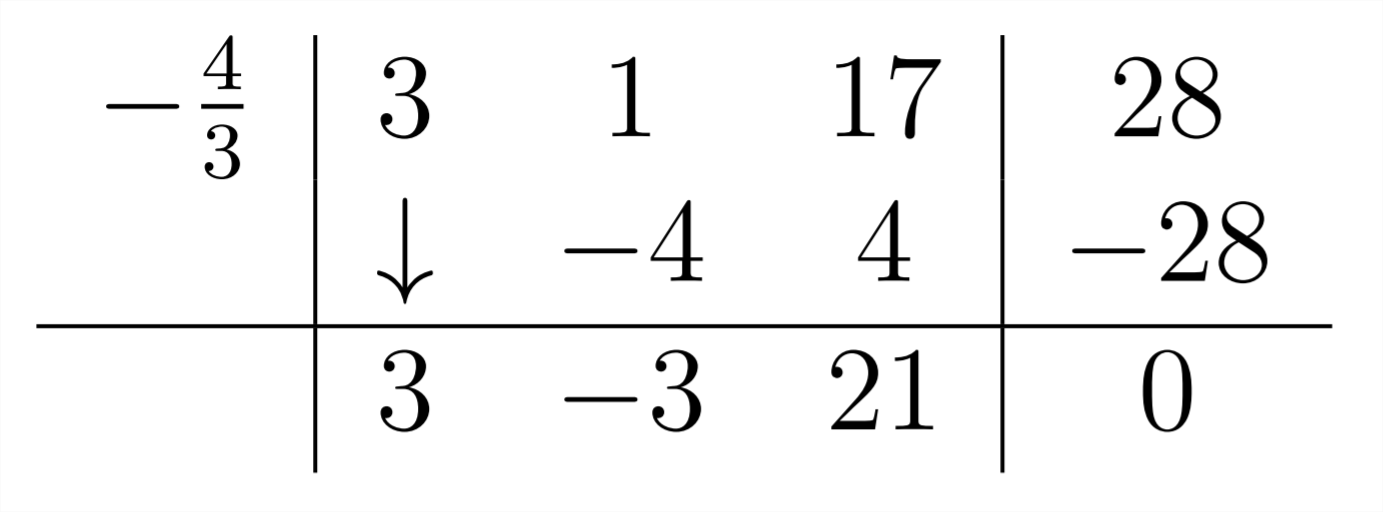
$clipboard_e07a5c59f1052a4ed07cd6226e14d47a0.png$
Notice that, because the root we used was a fraction, there is a common factor of 3 in the answer to our Synthetic Division. We should factor this out to obtain the
answer:
$\left(x+\frac{4}{3}\right)\left(3 x^{2}-3 x+21\right)=(3 x+4)\left(x^{2}-x+7\right)$
So, this means that:
\begin{array}{c}
3 x^{3}+x^{2}+17 x+28=0 \\
(3 x+4)\left(x^{2}-x+7\right)=0 \\
3 x+4=0 \quad x^{2}-x+7=0 \\
x=-\frac{4}{3} \quad x \approx 0.5 \pm 2.598 i
\end{array}

Exercises 2.8
Find all real and complex roots for the given equation. Express the given polynomial as the product of prime factors with integer coefficients.
Set #1
1) $x^{4}-3 x^{3}+5 x^{2}-x-10=0$
2) $3 x^{3}-5 x^{2}+2 x-8=0$
3) $2 x^{4}-5 x^{3}+x^{2}+4 x-4=0$
4) $x^{4}+x^{3}-3 x^{2}-17 x-30=0$
5) $x^{4}-9 x^{3}+21 x^{2}+21 x-130=0$
6) $x^{4}-7 x^{3}+14 x^{2}-38 x-60=0$
7) $x^{5}-9 x^{4}+31 x^{3}-49 x^{2}+36 x-10=0$
8) $x^{4}+4 x^{3}+2 x^{2}+12 x+45=0$
9) $x^{4}-6 x^{3}+12 x^{2}-10 x+3=0$
10) $x^{4}-6 x^{3}+13 x^{2}-24 x+36=0$
11) $x^{5}-3 x^{4}+12 x^{3}-28 x^{2}+27 x-9=0$
12) $x^{5}+2 x^{4}-3 x^{3}-3 x^{2}+2 x+1=0$
Set $\# 2$
13) $\quad 15 x^{3}-7 x^{2}+13 x+3=0$
14) $\quad x^{4}-5 x^{3}+3 x^{2}-11 x-20=0$
15) $\quad 6 x^{3}+13 x^{2}+12 x+4=0$
16) $\quad 6 x^{3}-5 x^{2}+5 x-2=0$
17) $\quad 4 x^{4}+20 x^{3}+29 x^{2}+10 x-15=0$
18) $\quad 3 x^{4}-4 x^{3}+10 x^{2}+12 x-5=0$
19) $\quad 2 x^{4}-3 x^{3}-6 x^{2}-8 x-3=0$
20) $\quad 12 x^{4}-53 x^{3}-31 x^{2}-19 x-5=0$
21) $\quad 12 x^{4}+4 x^{3}+x^{2}-3 x-2=0$
22) $\quad 3 x^{4}+13 x^{3}-26 x-40=0$