4.9: Optimization

Last updated
Save as PDF

Page ID: 40922

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

One of the major applications of differential calculus is optimization. This is the process of finding maximum or minimum function values for a given relationship. There are four typical types of problems that we will examine in this section.
a) Analytic Optimization - these problems typically use the distance formula to determine the closest point to a particular curve.

b) Geometry/cost Optimization - these problems generally give a box or container of a particular shape and ask either to determine the cheapest manufacturing cost given a particular volume or to determine the greatest volume given a particular cost.

c) Distance Optimization - these problems generally use two objects travelling at right angles to each other and determine the maximum or minimum distance between the objects.

d) Distance/cost Optimization - these problems are usually focused on a situation in which two distances at right angles can be cut with a diagonal at a certain point to minimize cost or time.

Analytic Optimization
\[
d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}
\]
1) Express the distance of a point $(x, y)$ (in the first quadrant) on the graph of the parabola $y=x^{2}-4$ from the point (5,2) as a function of $x$
2) Use the graph of the distance function $d(x)$ from Part I to determine the point of the graph of the parabola $y=x^{2}-4$ that is closest to the point (5,2)
3) How far is this point from the point (5,2)$?$
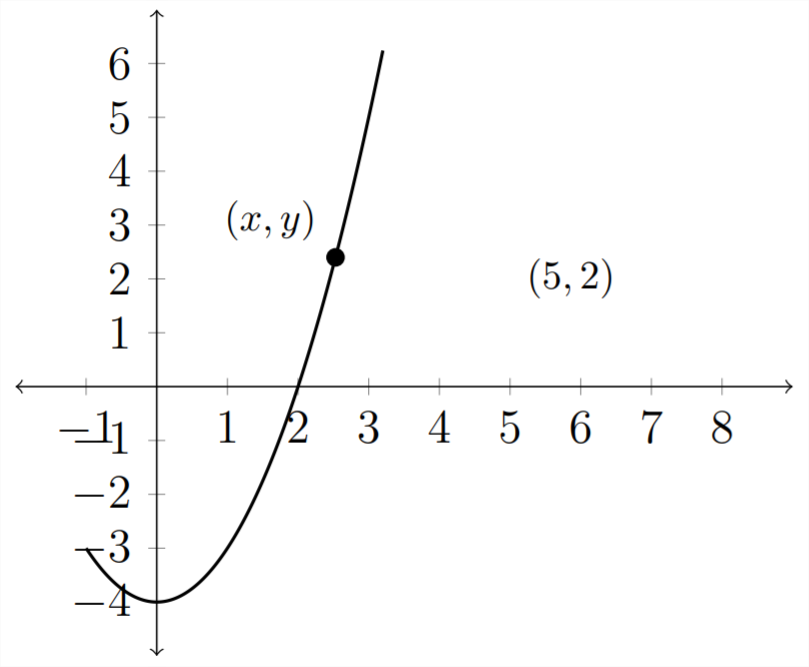
$clipboard_e77dd5a4742465589dcf46a0206809e77.png$
1) Using the distance formula $d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}},$ we can say that any point on the curve $y=x^{2}-4$ is a distance of:
\[
d=\sqrt{(x-5)^{2}+(y-2)^{2}}
\]
from the point $(5,2) .$ Because the question asks for this to be expressed as a function of $x,$ we should replace the $y$ variable with an equivalent expression involving $x$
\[
\begin{array}{c}
d=\sqrt{(x-5)^{2}+\left(x^{2}-4-2\right)^{2}} \\
\text { or } \\
d=\sqrt{(x-5)^{2}+\left(x^{2}-6\right)^{2}}
\end{array}
\]

2) The graph of this distance function is below:
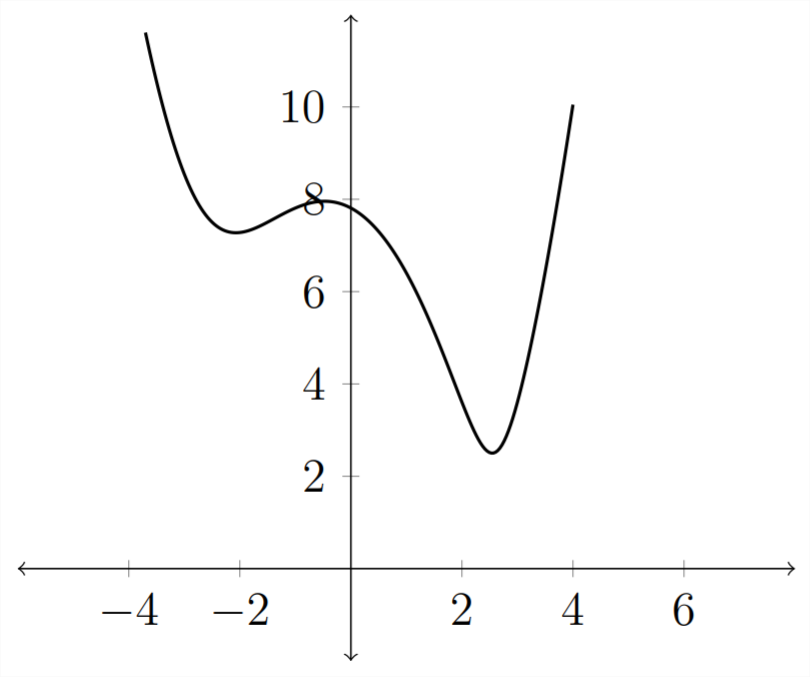
$clipboard_e3b603f080c13b1f6de005b109ebee647.png$
Note that in this graph, the $x$ axis represents the $x$ values from the original graph, but the $y$ axis in this graph is the distance of a point on the original curve from the point $(5,2) .$ We can see that this distance function has a clear minimum value that occurs between $x=2$ and $x=4 .$ We can use the graphing calculator to find this value - in Calculus we would use algebra to find this value.
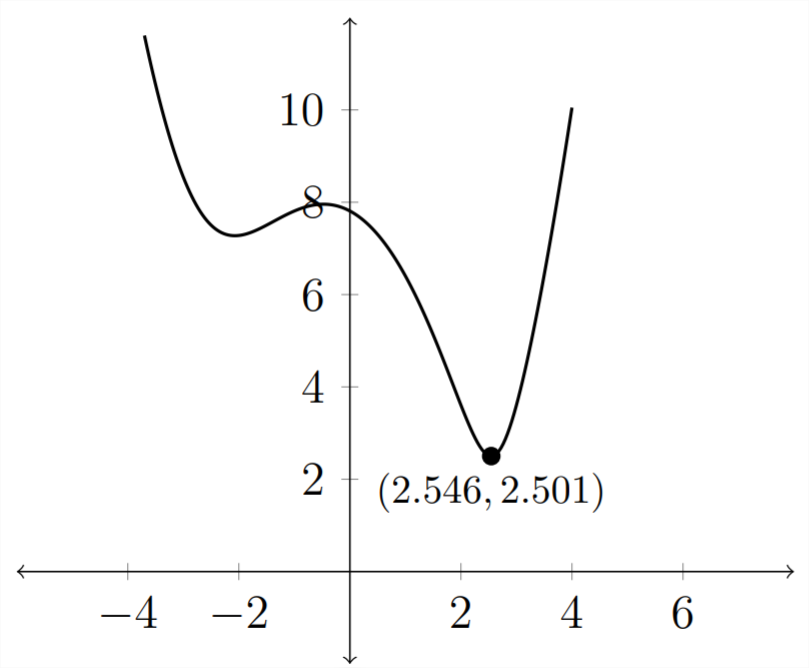
$clipboard_ed564b29313f15e8baf2048d0f743b1e1.png$
Both values indicated in the graph are approximate. The value $x \approx 2.546$ indicates the $x$ value of the point on the original curve that is closest to the point (5,2) The $y \approx 2.501$ indicates the distance of the point from the point (5,2)
since the $x$ value of the point on the original curve that is closest to the point (5,2) is about $2.546,$ that means that the $y$ value is:
\[
y=x^{2}-4 \approx 2.546^{2}-4 \approx 6.482-4 \approx 2.482
\]
So the answer for Part 2 is that (2.546,2.482) is closest point on the curve $y=x^{2}-4$ to the point (5,2)
3) We already determined the distance when we found the minimum point on the distance graph. The distance is about 2.501 units.

Exercises $4.9(a)$
1) Given the function $f(x)=4-x^{2}$, find $x$ and $y$ coordinates of the point on the curve that is closest to the point $(7,3) .$ How far away from the point (7,3) is the point you found?
2) Given the function $f(x)=6-x^{2},$ find $x$ and $y$ coordinates of the point on the curve that is closest to the point $(1,1) .$ How far away from the point (1,1) is the point you found?
3) Given the function $f(x)=x^{2}+2 x-5,$ find $x$ and $y$ coordinates of the point
on the curve that is closest to the point $(-2,5) .$ How far away from the point (-2,5) is the point you found?
4) Given the function $f(x)=x^{2}-5 x+8,$ find $x$ and $y$ coordinates of the point on the curve that is closest to the point $(-2,2) .$ How far away from the point (-2,2) is the point you found?
5) Given the function $f(x)=x^{3}-4 x^{2}+2 x+1,$ find $x$ and $y$ coordinates of the point on the curve that is closest to the point $(2,1) .$ How far away from the point
(2,1) is the point you found?
6) Given the function $f(x)=2 x^{3}-5 x-1,$ find $x$ and $y$ coordinates of the point
on the curve that is closest to the point $(-2,8) .$ How far away from the point (-2,8) is the point you found?
7) A rectangle has one corner in the 1 st quadrant on the graph of $y=16-x^{2}$ one corner at the origin and the other two corners on the positive $x$ axis and the positive $y$ axis.
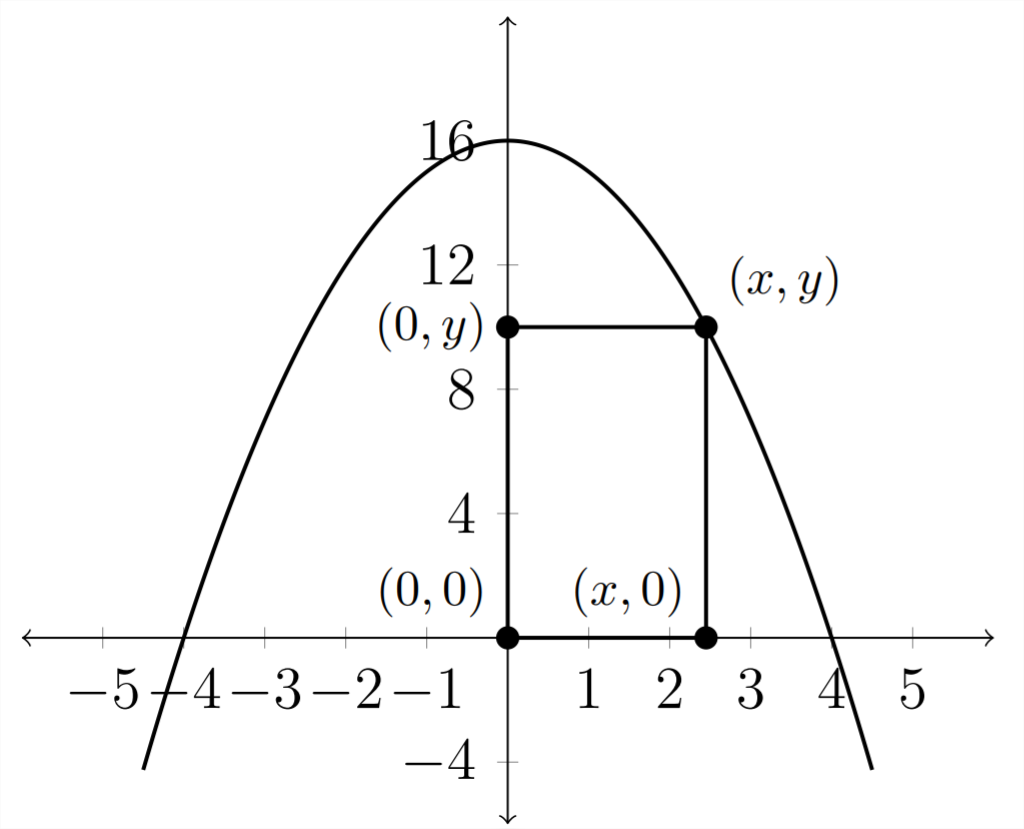
$clipboard_edd7efcab8fd1498b082c528ca5f3c240.png$
a) Express the area $A$ of the rectangle as a function of $x$.
b) For what value of $x$ is the area largest?
c) What is the maximum area?

8) A rectangle is inscribed in a semi-circle of radius 5 so that two corners are on the $x$ axis and two corners are on the semi-circle.
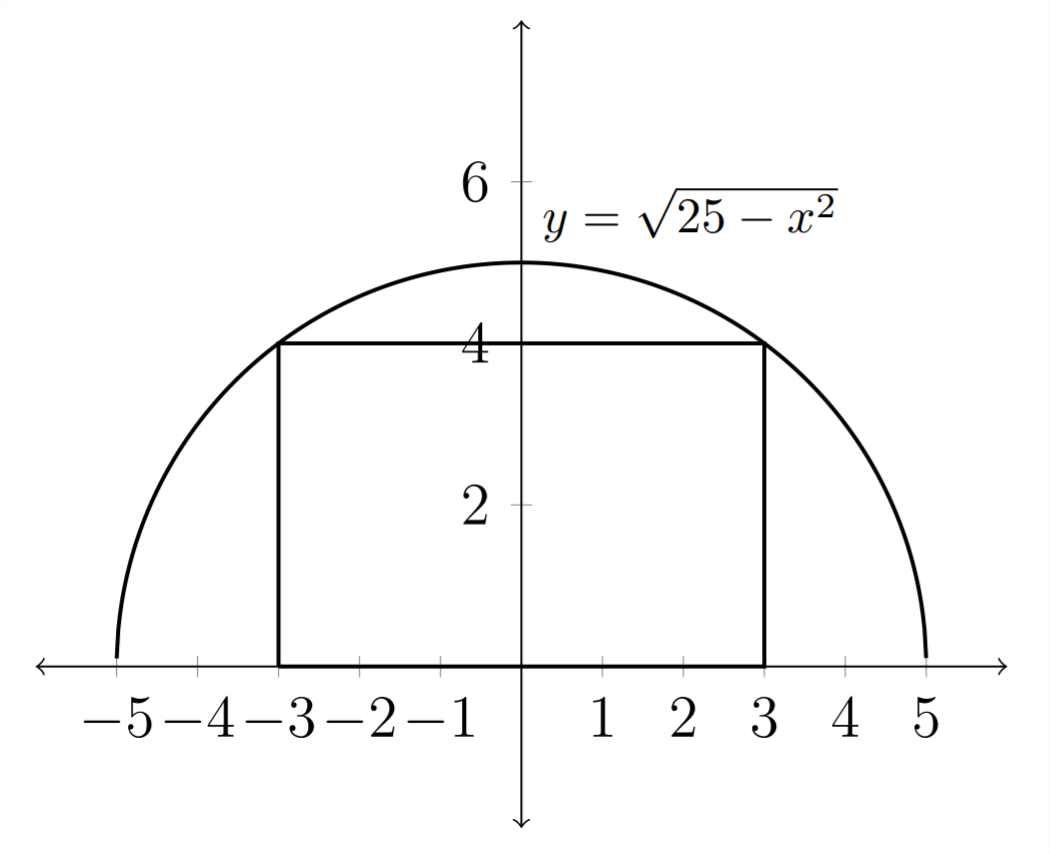
$clipboard_e652563c536276598174806a09ab77b0e.png$

The formula for the graph of the semi-circle is $y=\sqrt{25-x^{2}}$
a) Express the area $A$ of the rectangle as a function of $x$.
b) For what value of $x$ is the area largest?
c) What is the maximum area?

Geometry/cost Optimization
A closed box with a square base is built from material that costs $\$ 1$ per $\mathrm{ft}^{2}$ for the four sides and the bottom and $\$ 5$ per $\mathrm{ft}^{2}$ for the top. What are the dimensions of the box of largest volume that can be constructed for $\$ 72 ?$

There are two issues we are working with in this problem - the volume of the box and the surface area of the box. The volume of the box is important because that's what we're looking to maximize. The surface area of the box is important because that's what will control the cost of the box - notice that the costs are given in terms of $\mathrm{ft}^{2}$ or square feet which is related to the surface area.

The box has a square base, but the height is some other dimension - $h$. So the volume of the box will be length $*$ width $*$ height, but since the box has a square base the length and width will be the same - we'll call them $x$. From this we see that the volume can be expressed as:
\[
V=x * x * h=x^{2} h
\]
For the cost of the box, we need to know the surface area. Each side of the box should be included - the base and the top have the same area ( $x^{2}$ ) because they are both squares that are $x$ units on each side. The four sides of the box are all rectangles that are $x$ by $h$ units. That means each one has an area of $x * h-$ so all four would be $4 * x * h$ or $4 x h$
This makes the surface area of the box:
\[
S=2 x^{2}+4 x h
\]
The cost of the box then will be:
\[
C=x^{2}(\$ 1)+x^{2}(\$ 5)+4 x h(\$ 1)
\]
Here we see the one $x^{2}$ is multiplied by $\$ 1,$ because the bottom will cost $\$ 1$ per $\mathrm{ft}^{2},$ but the other $x^{2}$ is multiplied by $\$ 5,$ because the top costs $\$ 5$ per $\mathrm{ft}^{2}$. The four sides : $4 x h$ is also multiplied by \$1.

So, our final formula for the cost is:
\[
C=6 x^{2}+4 x h
\]
but we already know that we want to spend $\$ 72$ on the box, so we can say that:
\[
72=6 x^{2}+4 x h
\]
This means that:
\[
\begin{array}{c}
\frac{72-6 x^{2}}{4 x}=h \\
\text { or } \\
\frac{18}{x}-1.5 x=h
\end{array}
\]
The reason why this is important is that it will allow us to express the volume of the box in terms of $x .$ Remember that the volume was:
\[
V=x^{2} h
\]
so now we can see that:
\[
\begin{array}{c}
V=x^{2}\left(\frac{18}{x}-1.5 x\right) \\
\text { or } \\
V=18 x-1.5 x^{3}
\end{array}
\]

The graph for this function is below:

We can see in the graph that the maximum volume given a cost of $\$ 72$ will be when the base of the box is 2 feet by 2 feet. The volume will be $24 \mathrm{ft}^{3}$ and the height will be 6 feet. So the answer to the question is $2 \mathrm{ft} \times 2 \mathrm{ft} \times 6 \mathrm{ft}$

Exercises $4.9$(b)
1) A rectangular storage container with an open top has a volume of $10 \mathrm{m}^{3}$. The length of its base is twice the width. Material for the base costs $\$ 10$ per square meter. The sides require material that costs $\$ 6$ per square meter. Find the cost of materials for the cheapest such container.
2) A poster is to contain $108 \mathrm{cm}^{2}$ of printed matter, with margins of $6 \mathrm{cm}$ each at the top and bottom of the page and $2 \mathrm{cm}$ on each side of the page. What is the minimum cost of the poster if it is to be made of material which costs $\$ 0.20$ per square centimeter?
3) If $1200 \mathrm{cm}^{2}$ of material is available to make a box with a square base and an open top, find the largest possible volume of the box.
4) $\quad A$ box with a square base and open top must have a volume of $32,000 \mathrm{cm}^{3}$ Find the dimensions of the box that minimizes the amount of material used.
5) A Norman window has the shape of a semi-circle on top of a rectangle so that the diameter of the semi-circle is the same as the width of the rectangle. Given that the perimeter of the window should be $30 \mathrm{ft}$, find the dimensions of the window that will admit the greatest amount of sunlight (maximize the area).
6) A rectangular box with no top is to be made from material costing $\$ 0.50$ per square foot. The width of the base is 5 ft and it will have a volume of $6 \mathrm{ft}^{3}$. What are the dimensions of the box that minimizes the cost? What is the cost of this box?
Surface Area of a cylinder $=2 \pi r^{2}+2 \pi r h$
Volume of a cylinder $=\pi r^{2} h$
7) A cylindrical can with a top will be made from 200 in $^{2}$ of tin. What would be the height and radius of the can of maximum volume?
8) A cylindrical can with a top will have a volume of $500 \mathrm{cm}^{3}$. If the sides and bottom cost $\$ 0.002$ per square $\mathrm{cm}$ and the top costs $\$ 0.0035$ per square $\mathrm{cm},$ find the dimensions of the least expensive can that will have a volume of $500 \mathrm{cm}^{3}$ How much does it cost to make this can?

Distance Optimization
One ship is 10 miles due east of a buoy and is sailing due west, towards the buoy at 12 mph. Another ship is 10 miles due south of the same buoy and sailing due north, also towards the buoy at 7 mph.
a) Write a function that represents the distance between the two ships in terms of
$t,$ the elapsed time in hours.
b) Graph the function and determine the value of $t$ when the ships are closest together. How far apart are the ships at this time?
Round the value of $t$ to the nearest 100 th of an hour.
Round the distance to the nearest tenth of a mile.
Here is a diagram that represents the problem:
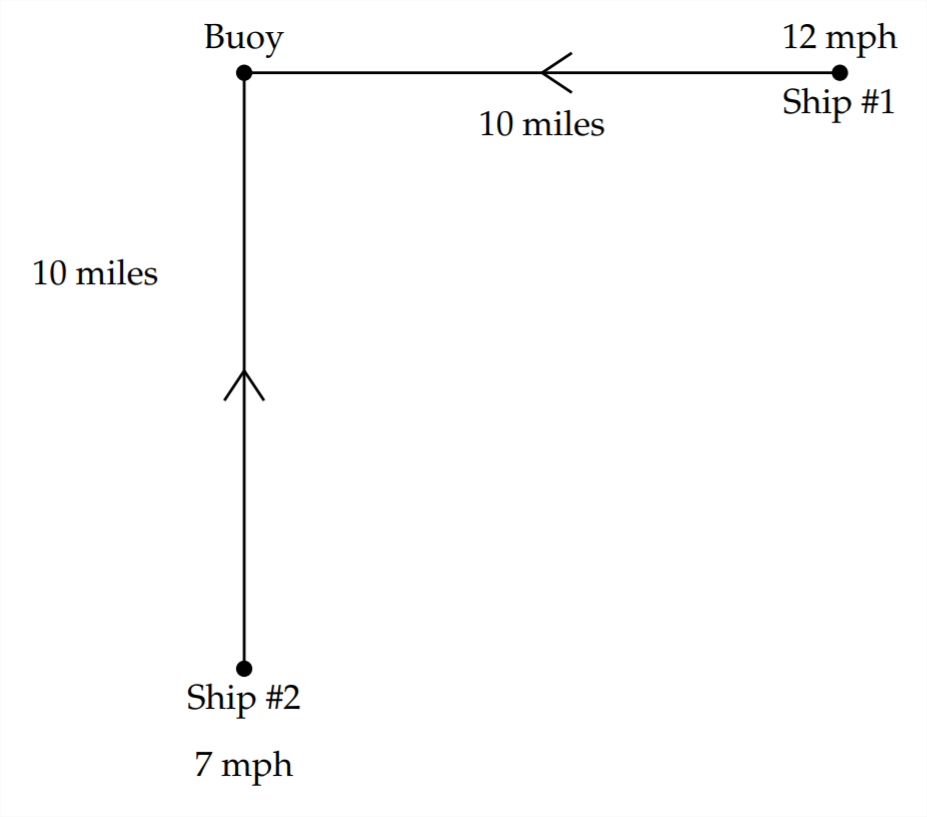
$clipboard_eb9e00c7329a1f1f445410b591e4a3238.png$
The distance between the two ships is measured along the diagonal. Because this creates a right triangle, we can use the Pythagorean Theorem to represent the distance between the ships.
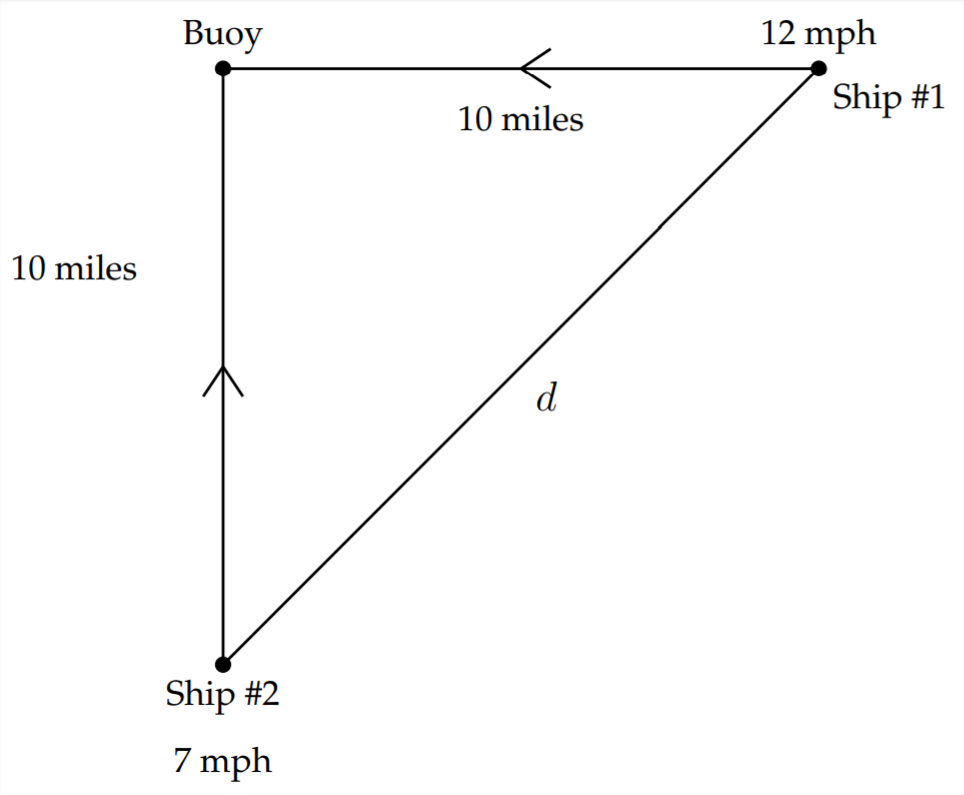
$clipboard_e74bee849393b3df7ec6a2df683b51955.png$

In this case the legs of the right triangle begin as 10 miles, but they get shorter as the ships travel closer to the buoy. For Ship #1, the distance decreases by 12 miles every hour - this means that the first ship will pass the buoy in less than one hour. The distance between Ship #1 and the buoy can be represented as $(10-12 t)$ where $t$ is the number of hours spent traveling. Similarly, the distance between Ship #2 and the buoy can be represented as $(10-7 t)$

So, using the Pythagorean Theorem, we can represent the distance between the ships at any given time as:
\[
d^{2}=(10-7 t)^{2}+(10-12 t)^{2}
\]
or
\[
d=\sqrt{(10-7 t)^{2}+(10-12 t)^{2}}
\]

The graph of this distance function looks like this:
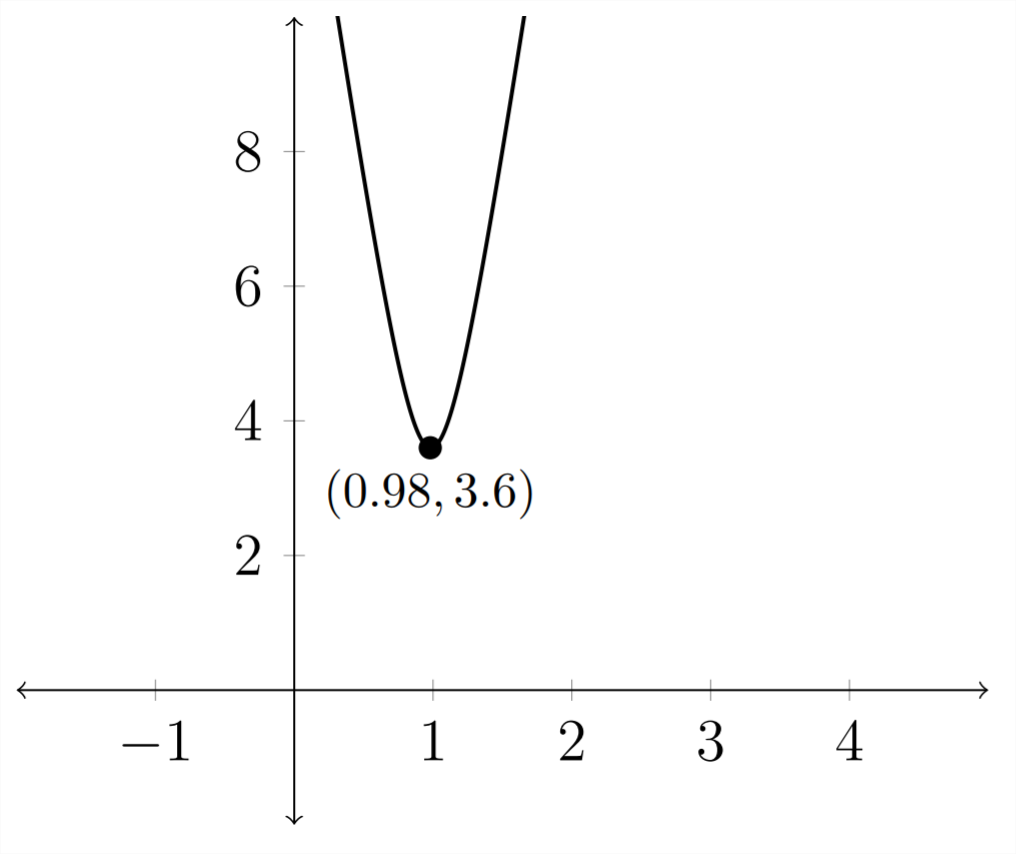
$clipboard_eb88a12d9da8ec2238680e51797cd86e5.png$
The minimum point on the distance graph indicates the time at which the ships are closest together. After traveling for 0.98 hours, the ships will be about 3.6 miles apart. They will then start moving farther apart.

Exercises $4.9(c)$
1) A runner starts running north from a given point running at 5 meters per second. At the same time, a second runner heads east from the same starting point, running at 8 meters per second. Represent the distance between the runners as a function of $t,$ the elapsed time. How long will it take for the runners to be 150 meters apart?

2) A runner starts running north from a given point running at 10 meters per second. At the same time, a second runner heads east from the same starting point, running at 7 meters per second. Represent the distance between the runners as a function of $t,$ the elapsed time. How long will it take for the runners to be 200 meters apart?

3) At $1 \mathrm{pm}$ a bicycle is 9 miles due north of an ice cream shop and is traveling south (towards the ice cream shop) at 15 mph. At the same time, another bike rider is 2 miles east of the ice cream shop and is traveling east (away from the ice cream shop) at 12 mph. Represent the distance between the bike riders at any given time after $1 \mathrm{pm}$. At what time is the distance between the riders at a minimum? How far apart are they at this point?

4) A car leaves a four-way intersection at 9: 15 am, traveling south at 70 mph. At the same time, another car is 65 miles west of the intersection traveling east at 55 mph. Express the distance between the two cars as a function of the time since they left the intersection. At what time are the cars closest together? How far apart from each other are they at this time?

At Noon, a dune buggy is in the desert at the point $A$ indicated below. Point $A$ is $40 \mathrm{km}$ from a paved road, which covers the $50 \mathrm{km}$ between points $\mathrm{B}$ and $\mathrm{D}$

If the dune buggy can travel 45 kph in the desert and 75 kph on the road, where is the best place for the driver to leave the desert and turn onto the road in order to minimize the travel time?

What time does the driver arrive at Point $D$ assuming they follow the path for minimal travel time?
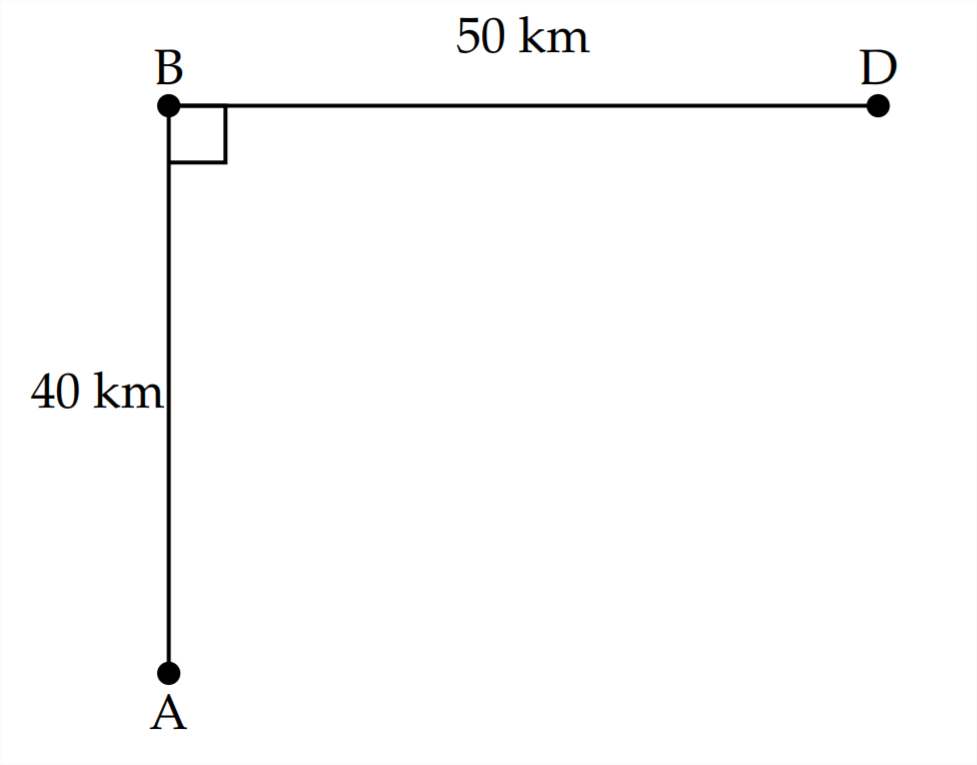
$clipboard_e68c08dcf1e02297969accf18f1362a8d.png$
One option is that the dune buggy can travel in a straight line from A to B (at 45 kph) and then travel on the paved road from $\mathrm{B}$ to $\mathrm{D}$ (at $75 \mathrm{kph}$ ). This would take $1.5 \mathrm{hrs}$
Another option is for the dune buggy to travel straight from A to D at 45 kph. The distance here is about $64 \mathrm{km}$ (found using the Pythagorean Theorem). That means the travel time would be about 1.423 hrs.

The optimization here says that, if the dune buggy were to travel part of the way in the desert (along a diagonal) and the rest of the way on the paved road, then there might be a minimal time that is shorter than the 1.423 hrs. it would take going straight from $\mathrm{A}$ to $\mathrm{D}$
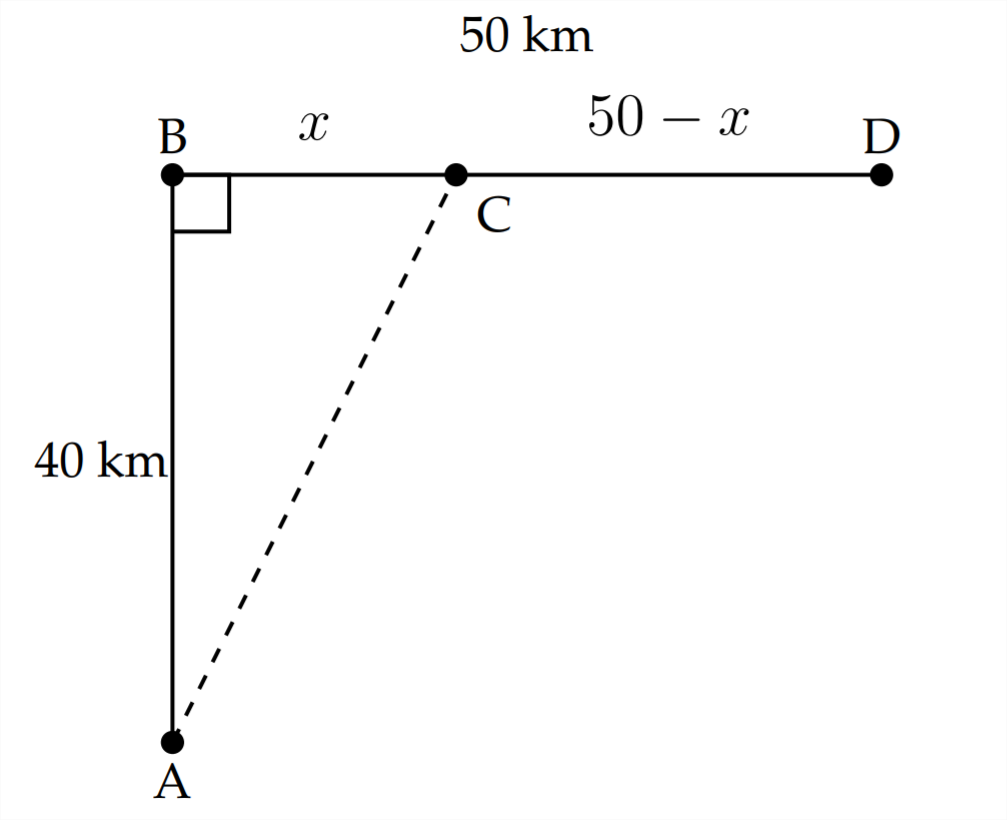
$clipboard_e2295318b695f61ac8d9ab88bb2320a63.png$
If we express the distance between $\mathrm{B}$ and $\mathrm{C}$ as $x,$ then the distance between $\mathrm{C}$ and D will be $50-x$. The distance travelled in the desert is the distance from A to $C$ and this is found using the Pythagorean Theorem.
\[
\overline{A C}=\sqrt{40^{2}+x^{2}}=\sqrt{x^{2}+1600}
\]
since $d=r * t,$ then the time it takes travel a given distance will be $\frac{d}{r}=t$
In the case of this problem the time to travel from A to C is:
\[
t_{1}=\frac{\sqrt{x^{2}+1600}}{45}
\]
The time to travel from $C$ to $D$ is:
\[
t_{2}=\frac{50-x}{75}
\]
So, the total travel time will be:
\[
t=t_{1}+t_{2}=\frac{x^{2}+1600}{45}+\frac{50-x}{75}
\]

The graph of this function is below:
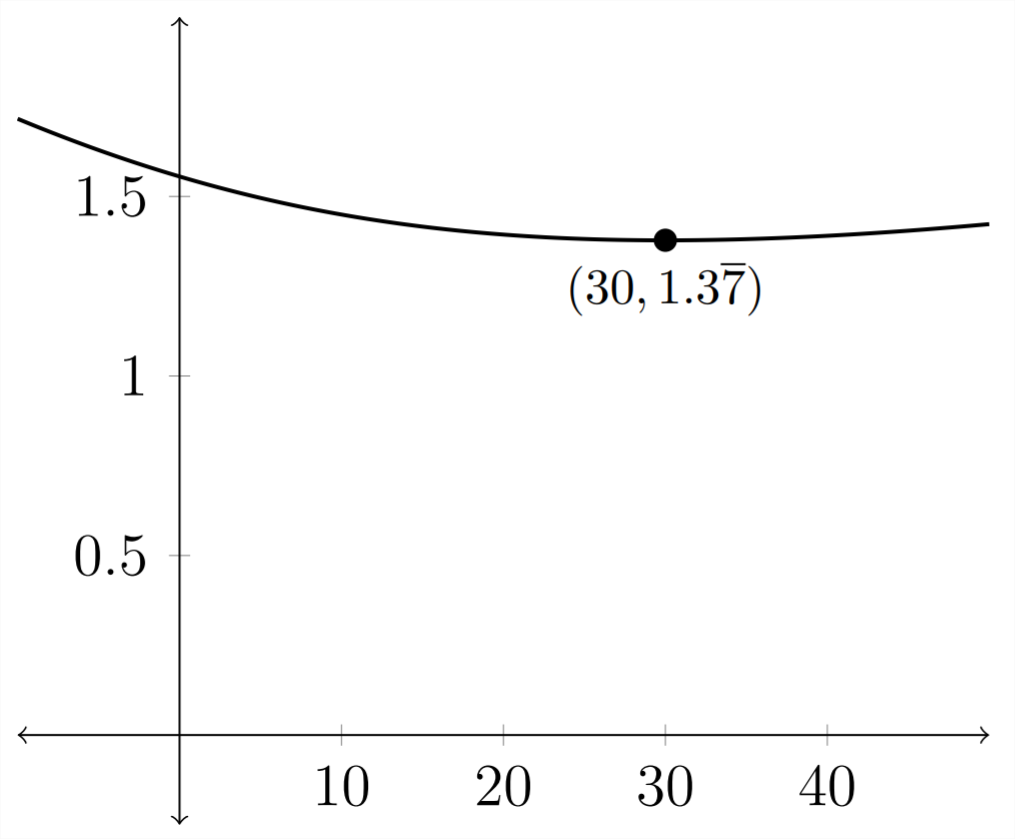
$clipboard_e2412b12667e8bcb0ec65a5eda119bfbd.png$
It is hard to see, but there is a minimum for the graph where $x=30$ and $t=1.3 \overline{7}$

Exercises $4.9(d)$
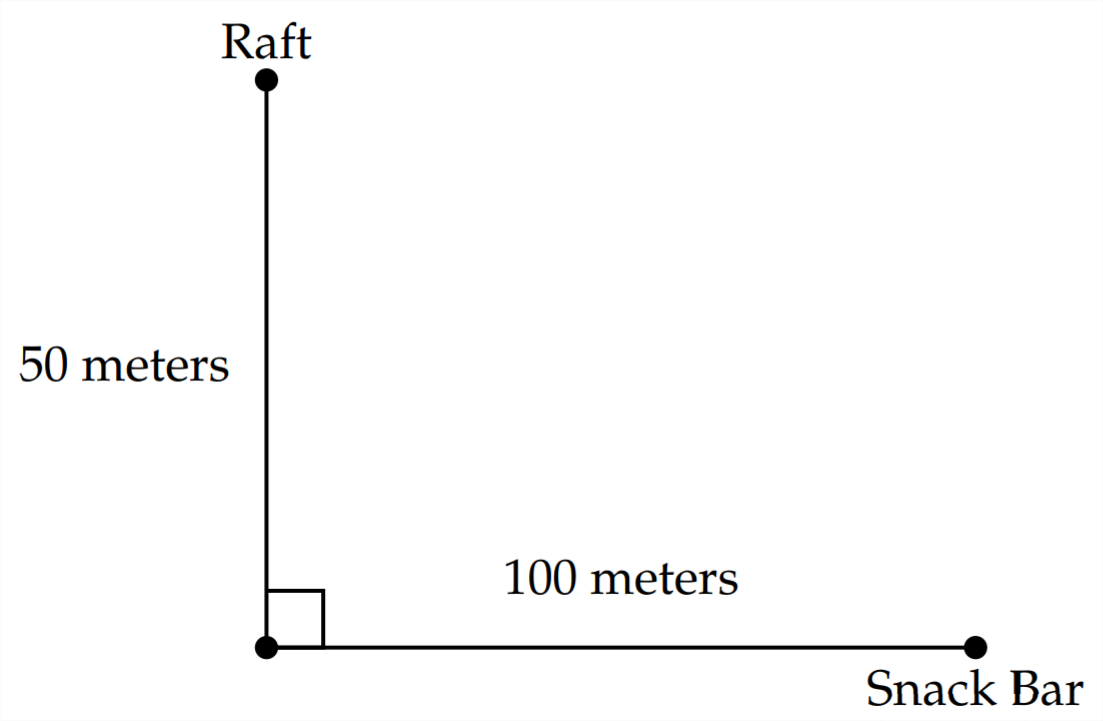
1) A woman wants to swim to shore from a raft that is 50 meters offshore and then run to the snack bar located 100 meters down the shoreline. The woman swims 1 meter per second and runs at 5 meters per second. Where on the shoreline should she swim to minimize her travel time?
$clipboard_ebe8f9a73ae39955568b3ebb25b6ab7ee.png$
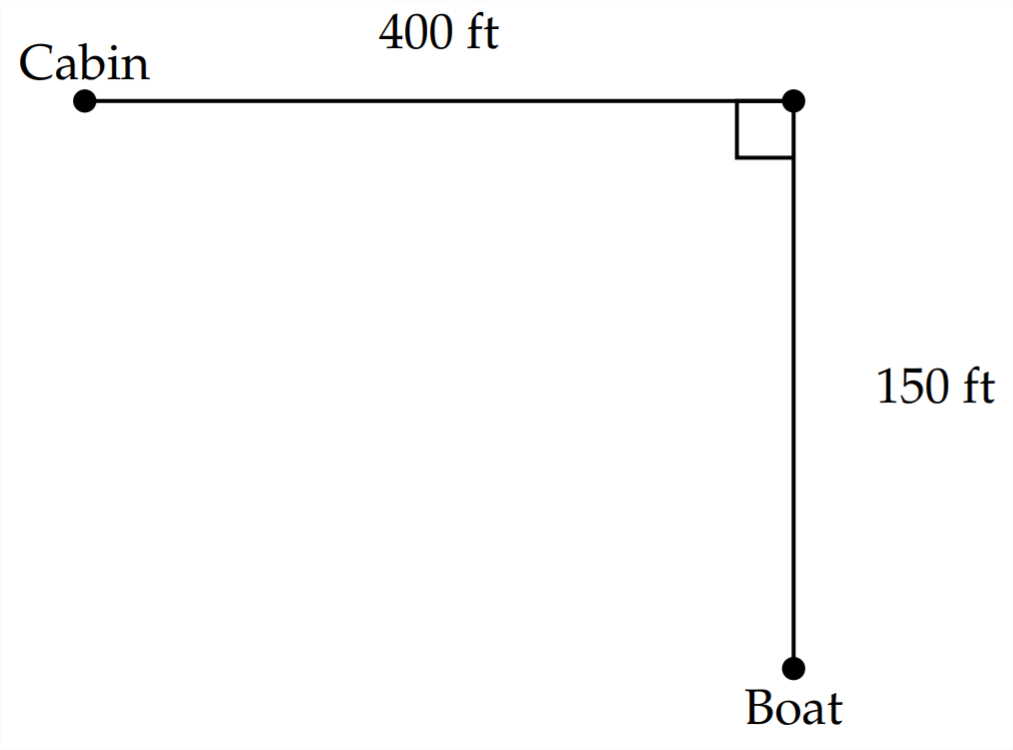
2) A man is in a boat on a lake $150 \mathrm{ft}$ from shore. He wants to return to his cabin. He is $400 \mathrm{ft}$ down the shoreline from the cabin. He plans to row to shore, leave the boat where he lands and then run the rest of the way to the cabin. If he rows 7 ft per second and runs 15 ft per second, where should he beach the rowboat to minimize the travel time?
$clipboard_e757f167e6800177b3679c37301149d65.png$
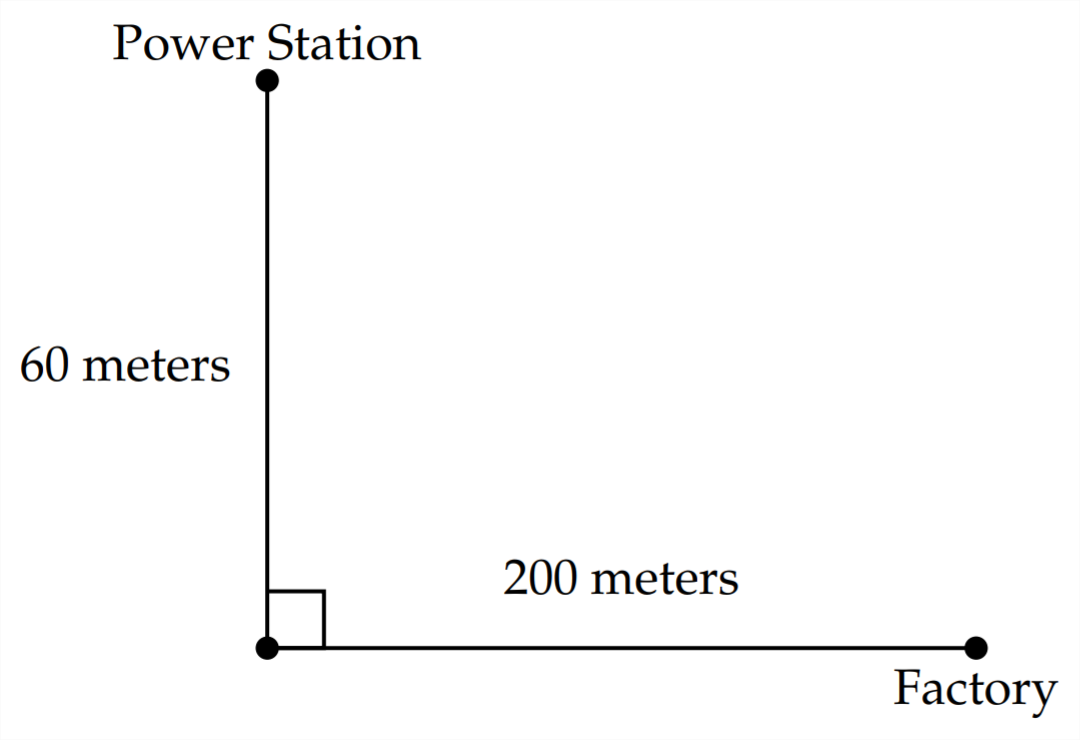
3) A power station and a factory are located on opposite sides of a river that is
60 meters wide. The factory is 200 meters from the point on the shore directly opposite the power station. A power line must be laid between the power station and the factory. It costs $\$ 25$ per meter to run the cable in the river and $\$ 20$ per meter to run the cable on the land. How much of the cable should be laid in the river and how much should be laid on land to minimize the cost? Where should the cable come ashore? What is the minimum cost?
$clipboard_eaaccebcfb6fc58fd516de178e73e5110.png$
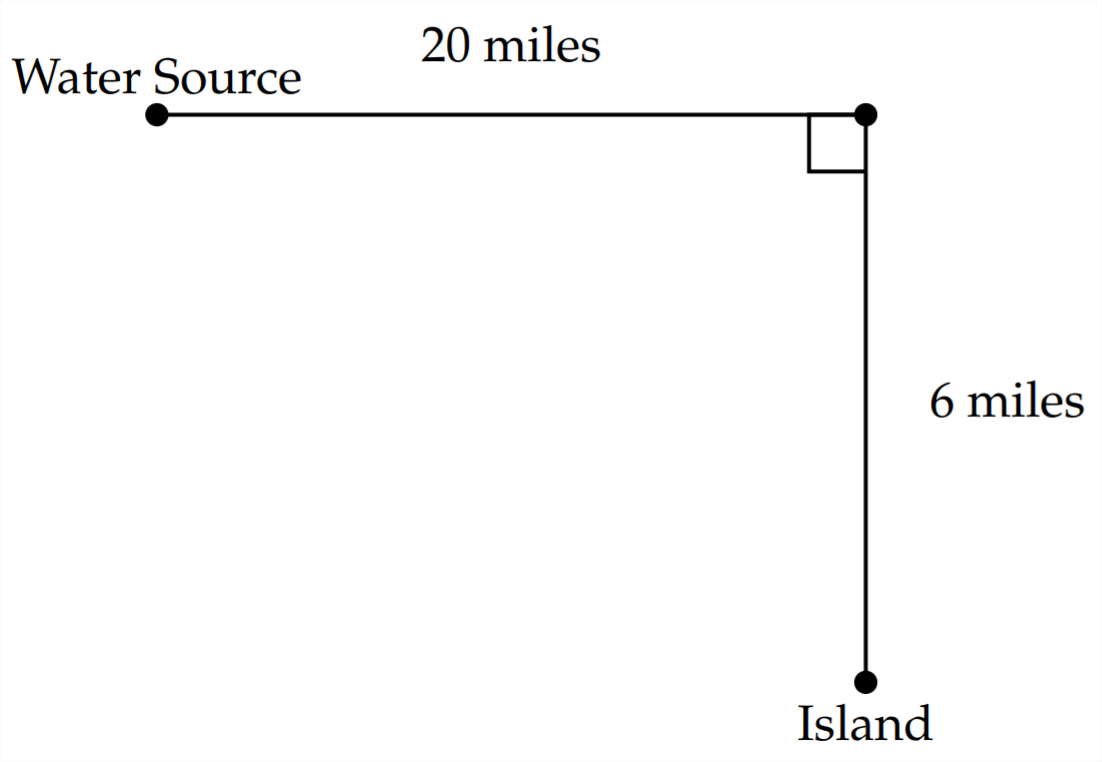
4) A freshwater pipeline is being constructed to an island that is 6 miles from the mainland. The water source is 20 miles down the coast from the point on the shore that is closest to the island. The cost of laying the pipeline along the shore is $\$ 8,000$ per mile while the cost of laying the pipeline in the water is $\$ 12,000$ per mile. How much of the pipeline should be laid in the water and how much should be laid on land to minimize the cost? Where should the pipeline leave the shore? What is the minimum cost?
$clipboard_e29d8f6003738a82bac68edfa3b657840.png$