2.E: Solving Linear Equations and Inequalities (Exercises)

Last updated
Save as PDF

Page ID: 20021

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

2.1: Solving Equations - One Step

In Exercises 1-6, which of the numbers following the given equation are solutions of the given equation? Support your response with work similar to that shown in Example 2.1.1.

1) $x+2=4 ; \quad 3,2,9,5$

Answer: $2$

2) $x+6=9 ; \quad 4,6,3,10$

3) $x-9=4 ; \quad 16,14,20,13$

Answer: $13$

4) $x-3=5 ; \quad 9,15,8,11$

5) $x-3=6 ; \quad 9,16,10,12$

Answer: $9$

6) $x-5=7 ; \quad 15,13,19,12$

In Exercises 7-12, are the following equations equivalent?

7) $x-1=-7$ and $x=-8$

Answer: No

8) $x-7=-8$ and $x=-15$

9) $x-5=-5$ and $x=0$

Answer: Yes

10) $x-3=-3$ and $x=0$

11) $x^{2}=1$ and $x=1$

Answer: No

12) $x^{2}=16$ and $x=4$

In Exercises 13-32, solve the given equation for $x$.

13) $x-20=9$

Answer: $29$

14) $x-10=5$

15) $16=x-3$

Answer: $19$

16) $16=x-8$

17) $x+11=20$

Answer: $9$

18) $x+10=18$

19) $9=x-19$

Answer: $28$

20) $4=x-11$

21) $20=9+x$

Answer: $11$

22) $18=7+x$

23) $18=17+x$

Answer: $1$

24) $15=7+x$

25) $7+x=19$

Answer: $12$

26) $16+x=17$

27) $x-9=7$

Answer: $16$

28) $x-2=8$

29) $x+15=19$

Answer: $4$

30) $x+6=10$

31) $10+x=15$

Answer: $5$

32) $18+x=19$

In Exercises 33-40, solve the equation and simplify your answer.

33) $x-\dfrac{4}{9}=\dfrac{2}{7}$

Answer: $\dfrac{46}{63}$

34) $x-\dfrac{1}{3}=\dfrac{1}{2}$

35) $x+\dfrac{7}{4}=-\dfrac{4}{9}$

Answer: $-\dfrac{79}{36}$

36) $x+\dfrac{1}{2}=-\dfrac{9}{7}$

37) $x+\dfrac{5}{9}=\dfrac{7}{2}$

Answer: $\dfrac{53}{18}$

38) $x+\dfrac{1}{4}=\dfrac{1}{3}$

39) $x-\dfrac{9}{8}=-\dfrac{1}{2}$

Answer: $\dfrac{5}{8}$

40) $x-\dfrac{5}{9}=-\dfrac{2}{3}$

In Exercises 41-46, solve the given equation for $x$.

41) $-5.1 x=-12.75$

Answer: $2.5$

42) $-3.5 x=-22.4$

43) $-6.9 x=-58.65$

Answer: $8.5$

44) $-1.4 x=-4.34$

45) $-3.6 x=-24.12$

Answer: $6.7$

46) $-6.4 x=-39.68$

In Exercises 47-52, solve the given equation for $x$.

47) $\dfrac{x}{2}=-11$

Answer: $-22$

48) $\dfrac{x}{8}=12$

49) $\dfrac{x}{8}=-18$

Answer: $-144$

50) $\dfrac{x}{-4}=-17$

51) $\dfrac{x}{-7}=15$

Answer: $-105$

52) $\dfrac{x}{8}=-7$

2.2: Solving Equations - Multiple Steps

In Exercises 1-16, solve the given equation for $x$.

1) $2 x-20=-12$

Answer: $4$

2) $-4 x-1=3$

3) $-11+3 x=-44$

Answer: $-11$

4) $-8+14 x=-22$

5) $-5 x+17=112$

Answer: $-19$

6) $3 x+12=51$

7) $-16 x-14=2$

Answer: $-1$

8) $4 x-4=64$

9) $5-13 x=70$

Answer: $-5$

10) $11+10 x=81$

11) $11+10 x=81$

Answer: $8$

12) $-4-16 x=-100$

13) $7-x=-7$

Answer: $14$

14) $20-3 x=35$

15) $-4 x+14=74$

Answer: $-15$

16) $-4 x+15=27$

In Exercises 17-24, solve the equation and simplify your answer.

17) $\dfrac{x}{7}-\dfrac{1}{3}=-\dfrac{9}{8}$

Answer: $-\dfrac{133}{24}$

18) $\dfrac{x}{8}-\dfrac{8}{3}=-\dfrac{4}{7}$

19) $\dfrac{x}{7}+\dfrac{4}{9}=\dfrac{3}{2}$

Answer: $\dfrac{133}{18}$

20) $\dfrac{x}{5}+\dfrac{1}{6}=\dfrac{8}{7}$

21) $\dfrac{x}{2}+\dfrac{2}{3}=\dfrac{4}{7}$

Answer: $-\dfrac{4}{21}$

22) $\dfrac{x}{7}+\dfrac{4}{5}=\dfrac{3}{4}$

23) $\dfrac{x}{5}-\dfrac{9}{2}=-\dfrac{5}{3}$

Answer: $\dfrac{85}{6}$

24) $\dfrac{x}{5}-\dfrac{8}{9}=-\dfrac{3}{2}$

In Exercises 26-32, solve each equation.

25) $0.3 x+1.7=3.05$

Answer: $4.5$

26) $-7.2 x+2.9=64.10$

27) $1.2 x+5.2=14.92$

Answer: $8.1$

28) $-7.3 x+1.8=-45.65$

29) $3.5 x-3.7=-26.10$

Answer: $-6.4$

30) $-1.4 x-4.7=5.80$

31) $-4.7 x-7.4=-48.29$

Answer: $8.7$

32) $-5.2 x-7.2=38.04$

In Exercises 33-44, solve each equation.

33) $13-9 x=11-5 x$

Answer: $\dfrac{1}{2}$

34) $11-10 x=13-4 x$

35) $11 x+10=19 x+20$

Answer: $-\dfrac{5}{4}$

36) $20 x+19=10 x+13$

37) $11-15 x=13-19 x$

Answer: $\dfrac{1}{2}$

38) $13-11 x=17-5 x$

39) $9 x+8=4-19 x$

Answer: $-\dfrac{1}{7}$

40) $10 x+8=6-2 x$

41) $7 x+11=16-18 x$

Answer: $\dfrac{1}{5}$

42) $11 x+8=2-17 x$

43) $12 x+9=4 x+7$

Answer: $-\dfrac{1}{4}$

44) $6 x+3=16 x+11$

In Exercises 45-56, solve each equation.

45) $8(5 x-3)-3(4 x+6)=4$

Answer: $\dfrac{23}{14}$

46) $6(3 x-8)-6(4 x+6)=3$

47) $2 x-4(4-9 x)=4(7 x+8)$

Answer: $\dfrac{24}{5}$

48) $4 x-9(6-2 x)=2(5 x+7)$

49) $2(6-2 x)-(4 x-9)=9$

Answer: $\dfrac{3}{2}$

50) $2(8-5 x)-(2 x-6)=4$

51) $3(5 x-6)-7(7 x+9)=3$

Answer: $-\dfrac{42}{17}$

52) $9(3 x-7)-9(2 x+9)=6$

53) $2 x-2(4-9 x)=8(6 x+2)$

Answer: $-\dfrac{6}{7}$

54) $3 x-3(5-9 x)=6(8 x+2)$

55) $2(7-9 x)-(2 x-8)=7$

Answer: $\dfrac{3}{4}$

56) $8(5-2 x)-(8 x-9)=4$

2.3: Clearing Fractions and Decimals

In Exercises 1-6, simplify the expression.

1) 16$\left(\dfrac{9}{2} x\right)$

Answer: $72x$

2) 27$\left(\dfrac{7}{9} x\right)$

3) 14$\left(\dfrac{3}{2} x\right)$

Answer: $21x$

4) $-12\left(\dfrac{9}{4} x\right)$

5) 70$\left(\dfrac{9}{7} x\right)$

Answer: $90x$

6) $-27\left(\dfrac{5}{3} x\right)$

In Exercises 7-18, for each of the following equations, clear fractions by multiplying both sides by the least common denominator. Solve the resulting equation for $x$ and reduce your answer to lowest terms.

7) $-\dfrac{9}{7} x-\dfrac{1}{3}=\dfrac{5}{3}$

Answer: $-\dfrac{14}{9}$

8) $-\dfrac{1}{2} x-\dfrac{3}{4}=-\dfrac{5}{9}$

9) $\dfrac{7}{3} x+\dfrac{5}{9}=\dfrac{2}{3} x-\dfrac{4}{3}$

Answer: $-\dfrac{17}{15}$

10) $\dfrac{2}{3} x-\dfrac{9}{4}=-\dfrac{5}{8} x-\dfrac{4}{3}$

11) $\dfrac{9}{4} x-\dfrac{8}{7}=\dfrac{3}{2}$

Answer: $\dfrac{74}{63}$

12) $-\dfrac{7}{3} x-\dfrac{2}{9}=-\dfrac{4}{3}$

13) $-\dfrac{3}{4} x=-\dfrac{8}{3}$

Answer: $\dfrac{32}{9}$

14) $-\dfrac{2}{3} x=\dfrac{5}{7}$

15) $x+\dfrac{3}{4}=\dfrac{6}{5}$

Answer: $\dfrac{9}{20}$

16) $x-\dfrac{2}{9}=\dfrac{1}{4}$

17) $-\dfrac{1}{3} x-\dfrac{4}{3}=-\dfrac{3}{4} x-\dfrac{8}{5}$

Answer: $-\dfrac{16}{25}$

18) $-\dfrac{6}{7} x-\dfrac{3}{5}=-\dfrac{9}{7} x-\dfrac{1}{2}$

In Exercises 19-32, clear decimals from the given equation by multiplying by the appropriate power of ten, then solve the resulting equation for $x$. Your ﬁnal answer should be a fraction reduced to lowest terms.

19) $2.39 x+0.71=-1.98 x+2.29$

Answer: $\dfrac{158}{437}$

20) $0.12 x+0.52=-1.47 x-2.12$

21) $0.4 x-1.55=2.14$

Answer: $\dfrac{369}{40}$

22) $0.8 x-2.18=1.49$

23) $2.6 x-2.54=-2.14 x$

Answer: $\dfrac{127}{237}$

24) $-1.4 x-2.98=0.55 x$

25) $0.7 x=-2.3 x-2.8$

Answer: $-\dfrac{14}{15}$

26) $3.4 x=1.8 x+2.5$

27) $-4.8 x-2.7=-1.9$

Answer: $-\dfrac{1}{6}$

28) $-2.4 x+2.5=2.3$

29) $1.7 x+2.1=-1.6 x+2.5$

Answer: $\dfrac{4}{33}$

30) $-1.2 x+0.4=-2.7 x-1.9$

31) $2.5 x+1.9=0.9 x$

Answer: $-\dfrac{19}{16}$

32) $4.4 x+0.8=2.8 x$

2.4: Formulae

In Exercises 1-30, solve the given formulas for the indicated variable.

1) $F=k x$ for $x$

Answer: $x=\dfrac{F}{k}$

2) $A=\pi r^{2}$ for $\pi$

3) $E=m c^{2}$ for $m$

Answer: $m=\dfrac{E}{c^{2}}$

4) $v=v_{0}+a t$ for $v_{0}$

5) $A=\pi r_{1} r_{2}$ for $r_{2}$

Answer: $r_{2}=\dfrac{A}{\pi r_{1}}$

6) $y=m x+b$ for $b$

7) $F=m a$ for $a$

Answer: $a=\dfrac{F}{m}$

8) $V=l w h$ for $l$

9) $C=2 \pi r$ for $r$

Answer: $r=\dfrac{C}{2 \pi}$

10) $F=k x$ for $k$

11) $y=m x+b$ for $x$

Answer: $x=\dfrac{y-b}{m}$

12) $I=\dfrac{V}{R}$ for $V$

13) $F=q v B$ for $v$

Answer: $v=\dfrac{F}{q B}$

14) $x+d=e$ for $x$

15) $V=\dfrac{1}{3} \pi r^{2} h$ for $h$

Answer: $h=\dfrac{3 V}{\pi r^{2}}$

16) $P=I R T$ for $I$

17) $I=\dfrac{V}{R}$ for $R$

Answer: $R=\dfrac{V}{I}$

18) $F=\dfrac{9}{5} C+32$ for $C$

19) $F=\dfrac{k q Q}{r^{2}}$ for $q$

Answer: $q=\dfrac{r^{2} F}{k Q}$

20) $A x+B y=C$ for $y$

21) $P=2 W+2 L$ for $W$

Answer: $W=\dfrac{P-2 L}{2}$

22) $A=\dfrac{1}{2} h\left(b_{1}+b_{2}\right)$ for $b_{1}$

23) $A=\dfrac{1}{2} h\left(b_{1}+b_{2}\right)$ for $h$

Answer: $h=\dfrac{2 A}{b_{1}+b_{2}}$

24) $A=\dfrac{a+b+c}{3}$ for $b$

25) $y-y_{0}=m\left(x-x_{0}\right)$ for $m$

Answer: $m=\dfrac{y-y_{0}}{x-x_{0}}$

26) $A=\dfrac{1}{2} b h$ for $b$

27) $F=\dfrac{G M m}{r^{2}}$ for $M$

Answer: $M=\dfrac{r^{2} F}{G m}$

28) $A=\dfrac{a+b+c}{3}$ for $a$

29) $d=v t$ for $v$

Answer: $v=\dfrac{d}{t}$

30) $x+d=e$ for $d$

31) Let $W$ and $L$ represent the width and length of a rectangle, respectively, and let $A$ represent its area.

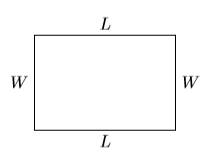
The area of the rectangle is given by the formula \[A = LW \nonumber \]Solve this formula for $L$. Then, given that the area of the rectangle is $A = 1073$ square meters and its width is $W = 29$ meters, determine its length.

Answer: $37$ square meters

32) Let $b_1$ and $b_2$ represent the parallel bases of a trapezoid and let $h$ represent its height.

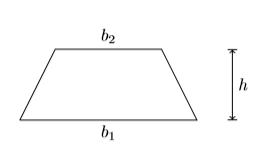
The area of the trapezoid is given by the formula:

\[A=\dfrac{1}{2}\left(b_{1}+b_{2}\right) h \nonumber \]

Solve this formula for $b_1$. Then, given that the area is $A = 2457$ square centimeters, the second base is $b_2 = 68$ centimeters, and the height is $h = 54$ centimeters, ﬁnd the length $b_1$ of the ﬁrst base.

33) A parallelogram is a quadrilateral (four sided ﬁgure) whose opposite sides are parallel.

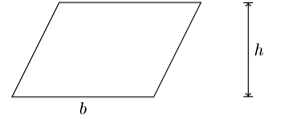
The area of the parallelogram is computed using the formula:

\[A = bh \nonumber \]

Solve this formula for $b$. Next, given that the area is $A = 2418$ square feet and the height is $h = 31$ feet, ﬁnd the length of the base of the parallelogram.

Answer: $78$ feet

34) Let $b_1$ and $b_2$ represent the parallel bases of a trapezoid and let $h$ represent its height.

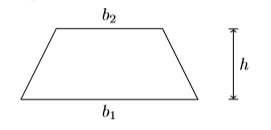
The area of the trapezoid is given by the formula:

\[A=\dfrac{1}{2}\left(b_{1}+b_{2}\right) h \nonumber \]

Solve this formula for $h$. Then, given that the area is $A = 3164$ square yards, the bases are $b_1 = 38$ yards and $b_2 = 75$ yards, ﬁnd the height $h$ of the trapezoid.

35) Let $b$ and $h$ represent the length of the base and the height of a triangle, respectively, and let $A$ represent the area of the triangle.

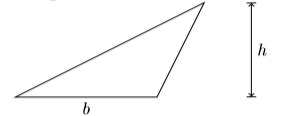
The area of the triangle is computed using the formula:

\[A=\dfrac{1}{2} b h \nonumber \]

Solve this formula for $b$. Next, given that the area is $A = 1332$ square inches and the height is $h = 36$ inches, ﬁnd the length of the base of the triangle.

Answer: $74$ inches

36) The circumference of a circle, somewhat like the term perimeter, is the distance around the circle. The diameter of a circle is a line segment drawn through the center of the circle.

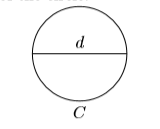
Since the time of the ancient Greeks, it has been known that the ratio of the circumference to the diameter is a constant, denoted by the symbol $\pi $.

\[\dfrac{C}{d}=\pi \nonumber \]

Solve the formula for $d$. Then, given $C = 188.4$ yards and $\pi =3.14$, ﬁnd the length of the diameter $d$.

37) Let $W$ and $L$ represent the width and length of a rectangle, respectively, and let $P$ represent its perimeter.

The perimeter (distance around) of the rectangle is found by summing its four sides, then combining like terms.

\[P =2W +2L \nonumber \]

Solve $P =2W +2L$ for $W$. Then, given that the perimeter is $P = 256$ meters and the length is $L = 73$ meters, use your result to calculate the width.

Answer: $55$ meters

2.5: Applications

1) Two angles are said to be complementary if their sum is ninety degrees. Suppose you have two complementary angles such that the second angle is $6$ degrees larger than $2$ times the measure of the ﬁrst angle. Find the angles.

Answer: $28$, $62$ degrees

2) Two angles are said to be complementary if their sum is ninety degrees. Suppose you have two complementary angles such that the second angle is $10$ degrees larger than $3$ times the measure of the ﬁrst angle. Find the angles.

3) Two angles are said to be supplementary if their sum is $180$ degrees. Suppose you have two supplementary angles such that the second angle is $10$ degrees larger than $4$ times the measure of the ﬁrst angle. Find the angles.

Answer: $34$, $146$ degrees

4) Two angles are said to be supplementary if their sum is $180$ degrees. Suppose you have two supplementary angles such that the second angle is $12$ degrees larger than $5$ times the measure of the ﬁrst angle. Find the angles.

5) The three sides of a triangle are consecutive integers. If the perimeter (sum of the three sides) of the triangle is $483$ meters, ﬁnd the length of each side of the triangle.

Answer: $160$, $161$, $162$ meters

6) The three sides of a triangle are consecutive integers. If the perimeter (sum of the three sides) of the triangle is $486$ yards, ﬁnd the length of each side of the triangle.

7) Four less than eight times a certain number is $−660$. Find the number.

Answer: $-82$

8) Nine less than ﬁve times a certain number is $141$. Find the number.

9) Alan is hiking a trail that is $70$ miles long. After several days, he is four times as far from the beginning of the trail as he is from the end. How much further does he have to hike?

Answer: $14$ miles

10) Joe is hiking a trail that is $30$ miles long. After several days, he is two times as far from the beginning of the trail as he is from the end. How much further does he have to hike?

11) Martha takes roll in her sixth grade grade class and ﬁnds that $2$ students are missing. If her actual class size is $36$ students, what percentage of her class is absent? Round your answer to the nearest percent.

Answer: $6\%$

12) Alice takes roll in her ﬁrst grade grade class and ﬁnds that $7$ students are missing. If her actual class size is $37$ students, what percentage of her class is absent? Round your answer to the nearest percent.

13) Lily cuts a piece of yarn into three pieces. The second pieces is $3$ times as long as the ﬁrst piece, and the third piece is 6 centimeters longer than the ﬁrst piece. If the total length of the yarn is $211$ centimeters, ﬁnd the lengths of each of the three pieces.

Answer: $41$, $123$, and $47$ centimeters

14) Jane cuts a piece of twine into three pieces. The second pieces is $7$ times as long as the ﬁrst piece, and the third piece is $5$ feet longer than the ﬁrst piece. If the total length of the twine is $320$ feet, ﬁnd the lengths of each of the three pieces.

15) The three sides of a triangle are consecutive even integers. If the perimeter (sum of the three sides) of the triangle is $450$ yards, ﬁnd the length of each side of the triangle.

Answer: $148$, $150$, $152$ yards

16) The three sides of a triangle are consecutive even integers. If the perimeter (sum of the three sides) of the triangle is $318$ feet, ﬁnd the length of each side of the triangle.

17) The perimeter of a triangle is $414$ yards. The second side of the triangle is $7$ times as long as the ﬁrst side and the third side of the triangle is $9$ yards longer than the ﬁrst side. Find the lengths of each of the three sides of the triangle.

Answer: $45$, $315$, and $54$ yards

18) The perimeter of a triangle is $54$ inches. The second side of the triangle is $2$ times as long as the ﬁrst side and the third side of the triangle is $6$ inches longer than the ﬁrst side. Find the lengths of each of the three sides of the triangle.

19) The sum of three consecutive odd integers is $−543$. Find the smallest of the three consecutive odd integers.

Answer: $-183$

20) The sum of three consecutive odd integers is $−225$. Find the smallest of the three consecutive odd integers.

21) The sum of the angles of a triangle is $180^{\circ}$. In triangle $\triangle A B C$, the degree measure of angle $B$ is $4$ times the degree measure of angle $A$. The degree measure of angle $C$ is $30$ degrees larger than the degree measure of angle $A$. Find the degree measures of each angle of triangle $\triangle A B C$.

Answer: $25^{\circ}, 100^{\circ}, 55^{\circ}$

22) The sum of the angles of a triangle is $180^{\circ}$. In triangle $\triangle A B C$, the degree measure of angle $B$ is $4$ times the degree measure of angle $A$. The degree measure of angle $C$ is $60$ degrees larger than the degree measure of angle $A$. Find the degree measures of each angle of triangle $\triangle A B C$.

23) The sum of three consecutive integers is $−384$. Find the largest of the three consecutive integers.

Answer: \(−127\

24) The sum of three consecutive integers is $−501$. Find the largest of the three consecutive integers.

25) Seven more than two times a certain number is $181$. Find the number.

Answer: $87$

26) Nine more than two times a certain number is $137$. Find the number.

27) The three sides of a triangle are consecutive odd integers. If the perimeter (sum of the three sides) of the triangle is $537$ feet, ﬁnd the length of each side of the triangle.

Answer: $177$, $179$, $181$ feet

28) The three sides of a triangle are consecutive odd integers. If the perimeter (sum of the three sides) of the triangle is $471$ centimeters, ﬁnd the length of each side of the triangle.

29) A store advertises that it is oﬀering a $14\%$ discount on all articles purchased at the store. If Yao pays $\$670.80$ for an article, what was the marked price for the article?

Answer: $\$ 780.00$

30) A store advertises that it is oﬀering a $12\%$ discount on all articles purchased at the store. If Roberto pays $\$560.56$ for an article, what was the marked price for the article?

31) The sum of three consecutive even integers is $−486$. Find the smallest of the three consecutive even integers.

Answer: $-164$

32) The sum of three consecutive even integers is $−354$. Find the smallest of the three consecutive even integers.

33) Burt inherits $\$45,500$. He decides to invest part of the inheritance in a mutual fund and the remaining part in a certiﬁcate of deposit. If the amount invested in the certiﬁcate of deposit is $\$3,500$ more than $6$ times the amount invested in the mutual fund, ﬁnd the amount invested in each account.

Answer: $\$ 6,000, \$ 39,500$

34) Phoenix inherits $\$12,000$. He decides to invest part of the inheritance in a mutual fund and the remaining part in a certiﬁcate of deposit. If the amount invested in the certiﬁcate of deposit is $\$3,000$ more than $8$ times the amount invested in the mutual fund, ﬁnd the amount invested in each account.

2.6: Inequalities

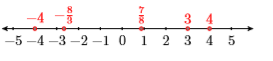
1) Draw a number line, then plot the numbers $4,3,-4,7 / 8$, and $−8/3$ on your number line. Label each point with its value. Finally, list the numbers in order, from smallest to largest.

Answer: $Ans 2.6.1.png$

2) Draw a number line, then plot the numbers $5,3,-4,5 / 7$, and $−4/3$ on your number line. Label each point with its value. Finally, list the numbers in order, from smallest to largest.

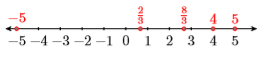
3) Draw a number line, then plot the numbers $-5,5,4,2 / 3$, and $8/3$ on your number line. Label each point with its value. Finally, list the numbers in order, from smallest to largest.

Answer: $Ans 2.6.3.png$

4) Draw a number line, then plot the numbers $-3,-2,4,1 / 3$, and $5/2$ on your number line. Label each point with its value. Finally, list the numbers in order, from smallest to largest.

In Exercises 5-20, shade each of the following sets on a number line.

5) $\{x : x \geq-7\}$

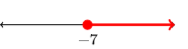
Answer: $Ans 2.6.5.png$

6) $\{x : x \geq-1\}$

7) $\{x : x<2\}$

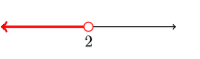
Answer: $Ans 2.6.7.png$

8) $\{x : x<-6\}$

9) $(-\infty, 2)$

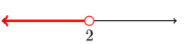
Answer: $Ans 2.6.9.png$

10) $(-\infty,-9)$

11) $(6, \infty)$

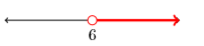
Answer: $Ans 2.6.11.png$

12) $(5, \infty)$

13) $\{x : x>7\}$

Answer: $Ans 2.6.13.png$

14) $\{x : x>-8\}$

15) $[0, \infty)$

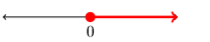
Answer: $Ans 2.6.15.png$

16) $[7, \infty)$

17) $\{x : x \leq-2\}$

Answer: $Ans 2.6.17.png$

18) $\{x : x \leq 7\}$

19) $(-\infty, 3]$

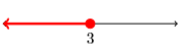
Answer: $Ans 2.6.19.png$

20) $(-\infty,-1]$

In Exercises 21-28, use set-builder notation to describe the shaded region on the given number line.

21)

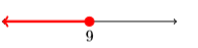
Answer: $\{x : x \leq 9\}$

22)

23)

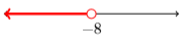
Answer: $\{x : x<-8\}$

24)

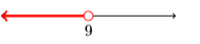
25)

Answer: $\{x : x>-2\}$

26)

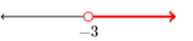
27)

Answer: $\{x : x \geq-3\}$

28)

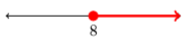
In Exercises 29-36, use interval notation to describe the shaded region on the given number line.

29)

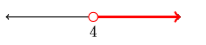
Answer: $(4, \infty)$

30)

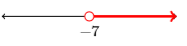
31)

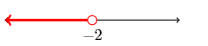
Answer: $(-\infty,-2)$

32)

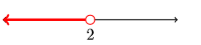
33)

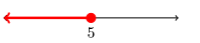
Answer: $(-\infty, 5]$

34)

35)

Answer: $[1, \infty)$

36)

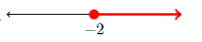
In Exercises 37-44, solve each of the given inequalities. Sketch the solution on a number line, then use set-builder and interval notation to describe your solution.

37) $x+10<19$

Answer: $(-\infty, 9)$

38) $x+17 \geq 7$

39) $4 x<8$

Answer: $(-\infty, 2)$

40) $16 x \geq-2$

41) $-2 x \leq-2$

Answer: $[1, \infty)$

42) $-18 x>-20$

43) $x-18>-10$

Answer: $(8, \infty)$

44) $x-8 \leq-18$

In Exercises 45-62, solve each of the given inequalities. Sketch the solution on a number line, then use set-builder and interval notation to describe your solution.

45) $-5 x-6 \geq 4-9 x$

Answer: $[5 / 2, \infty)$

46) $2 x-7 \geq-3-4 x$

47) $16 x-6 \leq 18$

Answer: $(-\infty, 3 / 2]$

48) $8 x-14 \leq-12$

49) $-14 x-6 \geq-10-4 x$

Answer: $(-\infty, 2 / 5]$

50) $-13 x-4 \geq-2-5 x$

51) $5 x+18<38$

Answer: $(-\infty, 4)$

52) $9 x+16<79$

53) $-16 x-5 \geq-11-6 x$

Answer: $(-\infty, 3 / 5]$

54) $-11 x-7 \geq-15-5 x$

55) $2 x-9 \geq 5-8 x$

Answer: $[7 / 5, \infty)$

56) $-3 x-6 \geq-2-9 x$

57) $-10 x-4 \leq 18$

Answer: $[-11 / 5, \infty)$

58) $-6 x-14 \leq 1$

59) $-12 x+4<-56$

Answer: $(5, \infty)$

60) $-18 x+6<-12$

61) $15 x+5<6 x+2$

Answer: $(-\infty,-1 / 3)$

62) $12 x+8<3 x+5$

In Exercises 63-76, solve each of the given inequalities. Sketch the solution on a number line, then use set-builder and interval notation describe your solution.

63) $\dfrac{3}{2} x>\dfrac{9}{8}$

Answer: $(3 / 4, \infty)$

64) $\dfrac{6}{7} x>\dfrac{3}{4}$

65) $x+\dfrac{3}{2}<\dfrac{9}{5}$

Answer: $(-\infty, 3 / 10)$

66) $x+\dfrac{1}{4}<-\dfrac{1}{5}$

67) $\dfrac{4}{7}-\dfrac{1}{6} x \leq \dfrac{4}{3} x-\dfrac{1}{2}$

Answer: $[5 / 7, \infty)$

68) $\dfrac{5}{3}-\dfrac{3}{4} x \leq \dfrac{7}{4} x-\dfrac{3}{5}$

69) $x-\dfrac{3}{8} \geq-\dfrac{9}{7}$

Answer: $[-51 / 56, \infty)$

70) $x-\dfrac{7}{2} \geq \dfrac{1}{5}$

71) $\dfrac{6}{5} x \leq-\dfrac{4}{7}$

Answer: $[10 / 21, \infty)$

72) $\dfrac{4}{3} x \leq \dfrac{2}{9}$

73) $-\dfrac{6}{5} x-\dfrac{7}{3} \leq \dfrac{5}{9}-\dfrac{2}{9} x$

Answer: $[-65 / 22, \infty)$

74) $-\dfrac{3}{7} x-\dfrac{1}{2} \leq \dfrac{3}{2}-\dfrac{2}{7} x$

75) $\dfrac{9}{7} x+\dfrac{9}{2}>\dfrac{1}{7} x+\dfrac{7}{2}$

Answer: $(-7 / 8, \infty)$

76) $\dfrac{5}{7} x+\dfrac{9}{2}>\dfrac{1}{3} x+\dfrac{5}{2}$

In Exercises 77-84, solve each of the given inequalities. Sketch the solution on a number line, then use set-builder and interval notation containing fractions in reduced form to describe your solution.

77) $-3.7 x-1.98 \leq 3.2$

Answer: $[-7 / 5, \infty)$

78) $-3.6 x-3.32 \leq 0.8$

79) $-3.4 x+3.5 \geq 0.9-2.2 x$

Answer: $(-\infty, 13 / 6]$

80) $-2.6 x+3.1 \geq-2.9-1.7 x$

81) $-1.3 x+2.9>-2.6-3.3 x$

Answer: $(-11 / 4, \infty)$

82) $2.5 x+2.1>1.4-3.8 x$

83) $2.2 x+1.9<-2.3$

Answer: $(-\infty,-21 / 11)$

84) $1.6 x+1.2<1.6$

Search

Text Color

Text Size

Margin Size

Font Type