5.E: Polynomial Functions (Exercises)

5.1: Functions

In Exercises 1-6, state the domain and range of the given relation.

1) $R=\{(7,4),(2,4),(4,2),(8,5)\}$

Answer

Domain $=\{2,4,7,8\}$ and Range $=\{2,4,5\}$

2) $S=\{(6,4),(3,3),(2,5),(8,7)\}$

3) $T=\{(7,2),(3,1),(9,4),(8,1)\}$

Answer

Domain $=\{3,7,8,9\}$ and Range $=\{1,2,4\}$

4) $R=\{(0,1),(8,2),(6,8),(9,3)\}$

5) $T=\{(4,7),(4,8),(5,0),(0,7)\}$

Answer

Domain $=\{0,4,5\}$ and Range $=\{0,7,8\}$

6) $T=\{(9,0),(3,6),(8,0),(3,8)\}$

In Exercises 7-10, state the domain and range of the given relation.

7)

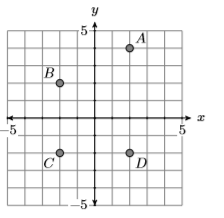
Answer

Domain $=\{-2,2\}$ and Range $=\{-2,2,4\}$

8)

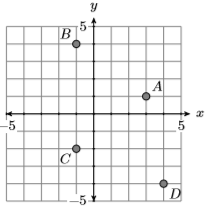
9)

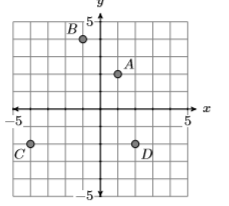
Answer

Domain $=\{-4,-1,1,2\}$ and Range $=\{-2,2,4\}$

10)

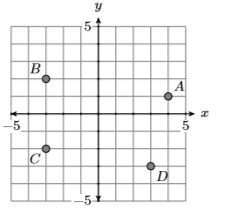
In Exercises 11-18, determine whether the given relation is a function.

11) $R=\{(-6,-4),(-4,-4),(1,-4)\}$

Answer

Function

12) $T=\{(-8,-3),(-4,-3),(2,-3)\}$

13) $T=\{(-1,-7),(2,-5),(4,-2)\}$

Answer

Function

14) $S=\{(-6,-6),(-4,0),(9,1)\}$

15) $T=\{(-9,1),(1,6),(1,8)\}$

Answer

Not a function

16) $S=\{(-7,0),(1,1),(1,2)\}$

17) $R=\{(-7,-8),(-7,-6),(-5,0)\}$

Answer

Not a function

18) $T=\{(-8,-9),(-8,-4),(-5,9)\}$

In Exercises 19-22, determine whether the given relation is a function.

19)

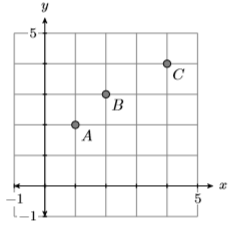
Answer

Function

20)

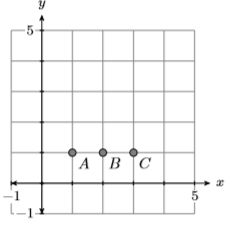
21)

Answer

Not a function

22)

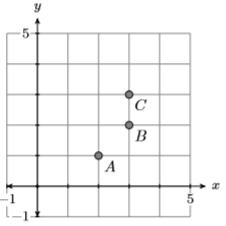
23) Given $f(x)=|6 x-9|$, evaluate $f(8)$.

Answer

$39$

24) Given $f(x)=|8 x-3|$, evaluate $f(5)$.

25) Given $f(x)=-2 x^{2}+8$, evaluate $f(3)$.

Answer

$-10$

26) Given $f(x)=3 x^{2}+x+6$, evaluate $f(-3)$.

27) Given $f(x)=-3 x^{2}+4 x+1$, evaluate $f(2)$.

Answer

$-3$

28) Given $f(x)=-3 x^{2}+4 x-2$, evaluate $f(2)$.

29) Given $f(x)=|5 x+9|$, evaluate $f(-8)$.

Answer

$31$

30) Given $f(x)=|9 x-6|$, evaluate $f(4)$.

31) Given $f(x)=\sqrt{x-6}$, evaluate $f(42)$.

Answer

$6$

32) Given $f(x)=\sqrt{x+8}$, evaluate $f(41)$.

33) Given $f(x)=\sqrt{x-7}$, evaluate $f(88)$.

Answer

$9$

34) Given $f(x)=\sqrt{x+9}$, evaluate $f(16)$.

35) Given $f(x)=-4 x+6$, evaluate $f(8)$.

Answer

$-26$

36) Given $f(x)=-9 x+2$, evaluate $f(-6)$.

37) Given $f(x)=-6 x+7$, evaluate $f(8)$.

Answer

$-41$

38) Given $f(x)=-6 x-2$, evaluate $f(5)$.

39) Given $f(x)=-2 x^{2}+3 x+2$ and $g(x)=3 x^{2}+5 x-5$, evaluate $f(3)$ and $g(3)$.

Answer

$f(3)=-7$ and $g(3)=37$

40) Given $f(x)=3 x^{2}-3 x-5$ and $g(x)=2 x^{2}-5 x-8$, evaluate $f(-2)$ and $g(-2)$.

41) Given $f(x)=6 x-2$ and $g(x)=-8 x+9$, evaluate $f(-7)$ and $g(-7)$.

Answer

$f(-7)=-44$ and $g(-7)=65$

42) Given $f(x)=5 x-3$ and $g(x)=9 x-9$, evaluate $f(-2)$ and $g(-2)$.

43) Given $f(x)=4 x-3$ and $g(x)=-3 x+8$, evaluate $f(-3)$ and $g(-3)$.

Answer

$f(-3)=-15$ and $g(-3)=17$

44) Given $f(x)=8 x+7$ and $g(x)=2 x-7$, evaluate $f(-9)$ and $g(-9)$.

45) Given $f(x)=-2 x^{2}+5 x-9$ and $g(x)=-2 x^{2}+3 x-4$, evaluate $f(-2)$ and $g(-2)$.

Answer

$f(-2)=-27$ and $g(-2)=-18$

46) Given $f(x)=-3 x^{2}+5 x-2$ and $g(x)=3 x^{2}-4 x+2$, evaluate $f(-1)$ and $g(-1)$.

5.2: Polynomials

In Exercises 1-6, state the coefficient and the degree of each of the following terms.

1) $3 v^{5} u^{6}$

Answer

Coefficient $=3,$ Degree $=11$

2) $-3 b^{5} z^{8}$

3) $-5 v^{6}$

Answer

Coefficient $=-5,$ Degree $=6$

4) $-5 c^{3}$

5) $2 u^{7} x^{4} d^{5}$

Answer

Coefficient $=2,$ Degree $=16$

6) $9 w^{4} c^{5} u^{7}$

In Exercises 7-16, state whether each of the following expressions is a monomial, binomial, or trinomial.

7) $-7 b^{9} c^{3}$

Answer

Monomial

8) $7 b^{6} c^{2}$

9) $4 u+7 v$

Answer

Binomial

10) $-3 b+5 c$

11) $3 b^{4}-9 b c+9 c^{2}$

Answer

Trinomial

12) $8 u^{4}+5 u v+3 v^{4}$

13) $5 s^{2}+9 t^{7}$

Answer

Binomial

14) $-8 x^{6}-6 y^{7}$

15) $2 u^{3}-5 u v-4 v^{4}$

Answer

Trinomial

16) $6 y^{3}-4 y z+7 z^{3}$

In Exercises 17-20, sort each of the given polynomials in descending powers of $x$.

17) $-2 x^{7}-9 x^{13}-6 x^{12}-7 x^{17}$

Answer

$-7 x^{17}-9 x^{13}-6 x^{12}-2 x^{7}$

18) $2 x^{4}-8 x^{19}+3 x^{10}-4 x^{2}$

19) $8 x^{6}+2 x^{15}-3 x^{11}-2 x^{2}$

Answer

$2 x^{15}-3 x^{11}+8 x^{6}-2 x^{2}$

20) $2 x^{6}-6 x^{7}-7 x^{15}-9 x^{18}$

In Exercises 21-24, sort each of the given polynomials in ascending powers of $x$.

21) $7 x^{17}+3 x^{4}-2 x^{12}+8 x^{14}$

Answer

$3 x^{4}-2 x^{12}+8 x^{14}+7 x^{17}$

22) $6 x^{18}-6 x^{4}-2 x^{19}-7 x^{14}$

23) $2 x^{13}+3 x^{18}+8 x^{7}+5 x^{4}$

Answer

$5 x^{4}+8 x^{7}+2 x^{13}+3 x^{18}$

24) $-6 x^{18}-8 x^{11}-9 x^{15}+5 x^{12}$

In Exercises 25-32, simplify the given polynomial, combining like terms, then arranging your answer in descending powers of $x$.

25) $-5 x+3-6 x^{3}+5 x^{2}-9 x+3-3 x^{2}+6 x^{3}$

Answer

$2 x^{2}-14 x+6$

26) $-2 x^{3}+8 x-x^{2}+5+7+6 x^{2}+4 x^{3}-9 x$

27) $4 x^{3}+6 x^{2}-8 x+1+8 x^{3}-7 x^{2}+5 x-8$

Answer

$12 x^{3}-x^{2}-3 x-7$

28) $-8 x^{3}-2 x^{2}-7 x-3+7 x^{3}-9 x^{2}-8 x+9$

29) $x^{2}+9 x-3+7 x^{2}-3 x-8$

Answer

$8 x^{2}+6 x-11$

30) $-4 x^{2}-6 x+3-3 x^{2}+3 x-6$

31) $8 x+7+2 x^{2}-8 x-3 x^{3}-x^{2}$

Answer

$-3 x^{3}+x^{2}+7$

32) $-x^{2}+8-7 x+8 x-5 x^{2}+4 x^{3}$

In Exercises 33-44, simplify the given polynomial, combining like terms, then arranging your answer in a reasonable order, perhaps in descending powers of either variable. Note: Answers may vary, depending on which variable you choose to dictate the order.

33) $-8 x^{2}-4 x z-2 z^{2}-3 x^{2}-8 x z+2 z^{2}$

Answer

$-11 x^{2}-12 x z$

34) $-5 x^{2}+9 x z-4 z^{2}-6 x^{2}-7 x z+7 z^{2}$

35) $-6 u^{3}+4 u v^{2}-2 v^{3}-u^{3}+6 u^{2} v-5 u v^{2}$

Answer

$-7 u^{3}+6 u^{2} v-u v^{2}-2 v^{3}$

36) $7 a^{3}+6 a^{2} b-5 a b^{2}+4 a^{3}+6 a^{2} b+6 b^{3}$

37) $-4 b^{2} c-3 b c^{2}-5 c^{3}+9 b^{3}-3 b^{2} c+5 b c^{2}$

Answer

$9 b^{3}-7 b^{2} c+2 b c^{2}-5 c^{3}$

38) $4 b^{3}-6 b^{2} c+9 b c^{2}-9 b^{3}-8 b c^{2}+3 c^{3}$

39) $-8 y^{2}+6 y z-7 z^{2}-2 y^{2}-3 y z-9 z^{2}$

Answer

$-10 y^{2}+3 y z-16 z^{2}$

40) $8 x^{2}+x y+3 y^{2}-x^{2}+7 x y+y^{2}$

41) $7 b^{2} c+8 b c^{2}-6 c^{3}-4 b^{3}+9 b c^{2}-6 c^{3}$

Answer

$-4 b^{3}+7 b^{2} c+17 b c^{2}-12 c^{3}$

42) $7 x^{3}-9 x^{2} y+3 y^{3}+7 x^{3}+3 x y^{2}-7 y^{3}$

43) $9 a^{2}+a c-9 c^{2}-5 a^{2}-2 a c+2 c^{2}$

Answer

$4 a^{2}-a c-7 c^{2}$

44) $7 u^{2}+3 u v-6 v^{2}-6 u^{2}+7 u v+6 v^{2}$

In Exercises 45-50, state the degree of the given polynomial.

45) $3 x^{15}+4+8 x^{3}-8 x^{19}$

Answer

$19$

46) $-4 x^{6}-7 x^{16}-5+3 x^{18}$

47) $7 x^{10}-3 x^{18}+9 x^{4}-6$

Answer

$18$

48) $3 x^{16}-8 x^{5}+x^{8}+7$

49) $-2-x^{7}-5 x^{5}+x^{10}$

Answer

$10$

50) $x^{11}+7 x^{16}+8-7 x^{10}$

51) Given $f(x)=5 x^{3}+4 x^{2}-6$, evaluate $f(-1)$.

Answer

$-7$

52) Given $f(x)=-3 x^{3}+3 x^{2}-9$, evaluate $f(-1)$.

53) Given $f(x)=5 x^{4}-4 x-6$, evaluate $f(-2)$.

Answer

$82$

54) Given $f(x)=-2 x^{4}-4 x-9$, evaluate $f(2)$.

55) Given $f(x)=3 x^{4}+5 x^{3}-9$, evaluate $f(-2)$.

Answer

$-1$

56) Given $f(x)=-3 x^{4}+2 x^{3}-6$, evaluate $f(-1)$.

57) Given $f(x)=3 x^{4}-5 x^{2}+8$, evaluate $f(-1)$.

Answer

$6$

58) Given $f(x)=-4 x^{4}-5 x^{2}-3$, evaluate $f(3)$.

59) Given $f(x)=-2 x^{3}+4 x-9$, evaluate $f(2)$.

Answer

$-17$

60) Given $f(x)=4 x^{3}+3 x+7$, evaluate $f(-2)$.

In Exercises 61-64, use your graphing calculator to sketch the the given quadratic polynomial. In each case the graph is a parabola, so adjust the WINDOW parameters until the vertex is visible in the viewing window, then follow the Calculator Submission Guidelines when reporting your solution on your homework.

61) $p(x)=-2 x^{2}+8 x+32$

Answer

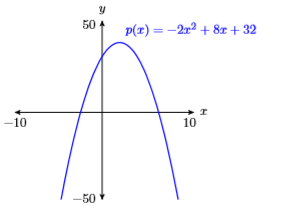
62) $p(x)=2 x^{2}+6 x-18$

63) $p(x)=3 x^{2}-8 x-35$

Answer

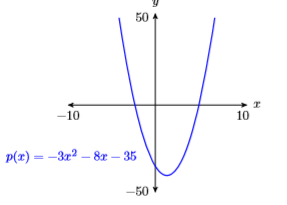
64) $p(x)=-4 x^{2}-9 x+50$

In Exercises 65-68, use your graphing calculator to sketch the polynomial using the given WINDOW parameters. Follow the Calculator Submission Guidelines when reporting your solution on your homework.

65) $p(x)=x^{3}-4 x^{2}-11 x+30$
$\mathbf{X} \min =-10 \quad \mathbf{X} \max =10$
$\mathbf{Y} \min =-50 \quad \mathbf{Y} \max =50$

Answer

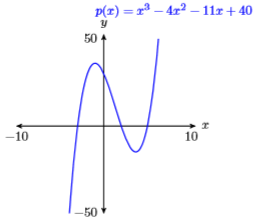
66) $p(x)=-x^{3}+4 x^{2}+27 x-90$
$\mathbf{X} \min =-10 \quad \mathbf{X} \max =10$
$\mathbf{Y} \min =-150 \quad \mathbf{Y} \max =50$

67) $p(x)=x^{4}-10 x^{3}-4 x^{2}+250 x-525$
$\mathbf{X} \min =-10 \quad \mathbf{X} \max =10$
$\mathbf{Y} \min =-1000 \quad \mathbf{Y} \max =500$

Answer

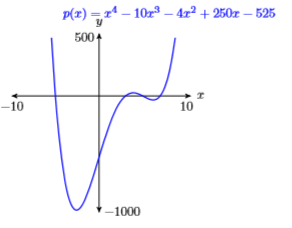
68) $p(x)=-x^{4}+2 x^{3}+35 x^{2}-36 x-180$
$\mathbf{X} \min =-10 \quad \mathbf{X} \max =10$
$\mathbf{Y} \min =-50 \quad \mathbf{Y} \max =50$

5.3: Applications of Polynomials

1) A firm collects data on the amount it spends on advertising and the resulting revenue collected by the firm. Both pieces of data are in thousands of dollars.

$x$ (advertising costs)	0	5	15	20	25	30
$R$ (revenue)	6347	6524	7591	8251	7623	7478

The data is plotted then fitted with the following second degree polynomial, where $x$ is the amount invested in thousands of dollars and $R(x)$ is the amount of revenue earned by the firm (also in thousands of dollars).

$R(x)=−4.1x^2 + 166.8x+ 6196$

Use the graph and then the polynomial to estimate the firm’s revenue when the firm invested $\$10,000$ in advertising.

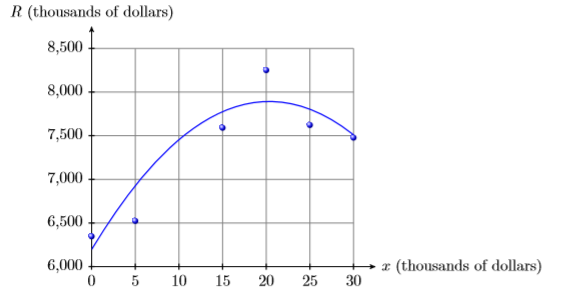
Answer

Approximately $\$7,454,000$

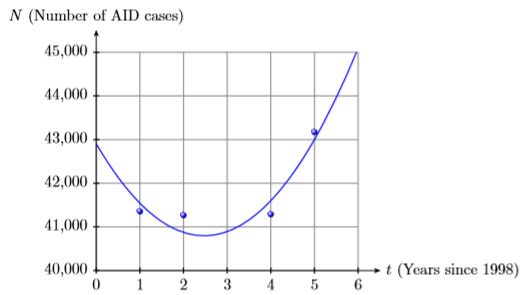
2) The table below lists the estimated number of aids cases in the United States for the years 1999-2003.

Year	1999	2000	2002	2003
AIDS Cases	41,356	41,267	41,289	43,171

The data is plotted then fitted with the following second degree polynomial, where $t$ is the number of years that have passed since 1998 and $N(t)$ is the number of aids case reported $t$ years after 1998.

$N(t) = 345.14t^2−1705.7t+ 42904$

Use the graph and then the polynomial to estimate the number of AIDS cases in the year 2001.

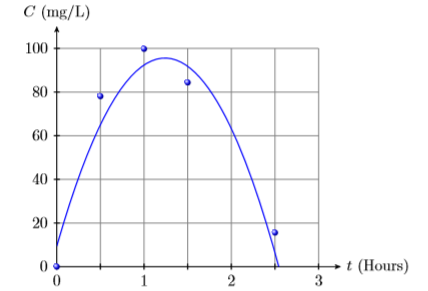
3) The following table records the concentration (in milligrams per liter) of medication in a patient’s blood after indicated times have passed.

Time (Hours)	0	0.5	1	0.5	2.5
Concentration(mg/L)	0	78.1	99.8	84.4	15.6

The data is plotted then fitted with the following second degree polynomial, where $t$ is the number of hours that have passed since taking the medication and $C(t)$ is the concentration (in milligrams per liter) of the medication in the patient’s blood after $t$ hours have passed.

$C(t)=−56.214t^2 + 139.31t+9.35$

Use the graph and then the polynomial to estimate the the concentration of medication in the patient’s blood $2$ hours after taking the medication.

Answer

Approximately $63 \mathrm{mg} / \mathrm{L}$

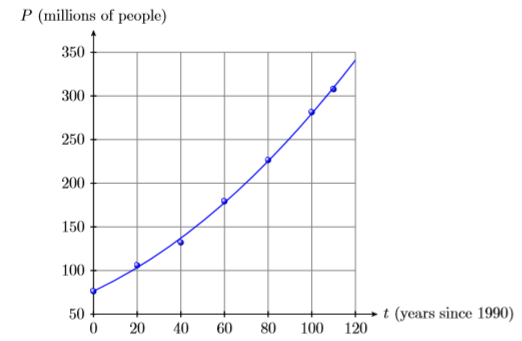
4) The following table records the population (in millions of people) of the United States for the given year.

Year	1900	1920	1940	1960	1980	2000	2010
Population (millions)	76.2	106.0	132.2	179.3	226.5	281.4	307.7

The data is plotted then fitted with the following second degree polynomial, where $t$ is the number of years that have passed since 1990 and $P(t)$ is the population (in millions) $t$ years after 1990.

$P(t)=0 .008597t^2 +1,1738t+ 76 .41$

Use the graph and then the polynomial to estimate the the population of the United States in the year 1970.

5) If a projectile is launched with an initial velocity of $457$ meters per second ($457 \mathrm{m/s}$) from a rooftop $75$ meters ($75 \mathrm{m}$) above ground level, at what time will the projectile first reach a height of $6592$ meters ($6592 \mathrm{m}$)? Round your answer to the nearest second.

Note: The acceleration due to gravity near the earth’s surface is $9.8$ meters per second per second ($9.8 \mathrm{m} / \mathrm{s}^{2}$).

Answer

$17.6$ seconds

6) If a projectile is launched with an initial velocity of $236$ meters per second ($236 \mathrm{m/s}$) from a rooftop $15$ meters ($15\mathrm{m}$) above ground level, at what time will the projectile first reach a height of $1838$ meters ($1838\mathrm{m}$)? Round your answer to the nearest second.

Note: The acceleration due to gravity near the earth’s surface is $9.8$ meters per second per second ($9.8 \mathrm{m} / \mathrm{s}^{2}$).

7) If a projectile is launched with an initial velocity of $229$ meters per second ($229 \mathrm{m/s}$) from a rooftop $58$ meters ($58\mathrm{m}$) above ground level, at what time will the projectile first reach a height of $1374$ meters ($1374\mathrm{m}$)? Round your answer to the nearest second.

Note: The acceleration due to gravity near the earth’s surface is 9.8 meters per second per second ($9.8 \mathrm{m} / \mathrm{s}^{2}$).

Answer

$6.7$ seconds

8) If a projectile is launched with an initial velocity of $234$ meters per second ($234 \mathrm{m/s}$) from a rooftop $16$ meters ($16\mathrm{m}$) above ground level, at what time will the projectile first reach a height of $1882$ meters ($1882\mathrm{m}$)? Round your answer to the nearest second.

Note: The acceleration due to gravity near the earth’s surface is $9.8$ meters per second per second ($9.8 \mathrm{m} / \mathrm{s}^{2}$).

In Exercises 9-12, first use an algebraic technique to find the zero of the given function, then use the 2:zero utility on your graphing calculator to locate the zero of the function. Use the Calculator Submission Guidelines when reporting the zero found using your graphing calculator.

9) $f(x)=3.25 x-4.875$

Answer

Zero: $1.5$

10) $f(x)=3.125-2.5 x$

11) $f(x)=3.9-1.5 x$

Answer

Zero: $2.6$

12) $f(x)=0.75 x+2.4$

13) If a projectile is launched with an initial velocity of $203$ meters per second ($203 \mathrm{m/s}$) from a rooftop $52$ meters ($52\mathrm{m}$) above ground level, at what time will the projectile return to ground level? Round your answer to the nearest tenth of a second.

Note: The acceleration due to gravity near the earth’s surface is $9.8$ meters per second per second ($9.8 \mathrm{m} / \mathrm{s}^{2}$).

Answer

$41.7$ seconds

14) If a projectile is launched with an initial velocity of $484$meters per second ($484 \mathrm{m/s}$) from a rooftop $17$ meters ($17\mathrm{m}$) above ground level, at what time will the projectile return to ground level? Round your answer to the nearest tenth of a second.

Note: The acceleration due to gravity near the earth’s surface is $9.8$ meters per second per second ($9.8 \mathrm{m} / \mathrm{s}^{2}$).

15) If a projectile is launched with an initial velocity of $276$ meters per second ($276 \mathrm{m/s}$) from a rooftop $52$ meters ($52\mathrm{m}$) above ground level, at what time will the projectile return to ground level? Round your answer to the nearest tenth of a second.

Note: The acceleration due to gravity near the earth’s surface is $9.8$ meters per second per second ($9.8 \mathrm{m} / \mathrm{s}^{2}$).

Answer

$56.5$ seconds

16) If a projectile is launched with an initial velocity of $204$ meters per second ($204 \mathrm{m/s}$) from a rooftop $92$ meters ($92\mathrm{m}$) above ground level, at what time will the projectile return to ground level? Round your answer to the nearest tenth of a second.

Note: The acceleration due to gravity near the earth’s surface is $9.8$ meters per second per second ($9.8 \mathrm{m} / \mathrm{s}^{2}$).

5.4: Adding and Subtracting Polynomials

In Exercises 1-8, simplify the given expression. Arrange your answer in some sort of reasonable order.

1) $\left(-8 r^{2} t+7 r t^{2}+3 t^{3}\right)+\left(9 r^{3}+2 r t^{2}+4 t^{3}\right)$

Answer

$9 r^{3}-8 r^{2} t+9 r t^{2}+7 t^{3}$

2) $\left(-a^{3}-8 a c^{2}-7 c^{3}\right)+\left(-7 a^{3}-8 a^{2} c+8 a c^{2}\right)$

3) $\left(7 x^{2}-6 x-9\right)+\left(8 x^{2}+10 x+9\right)$

Answer

$15 x^{2}+4 x$

4) $\left(-7 x^{2}+5 x-6\right)+\left(-10 x^{2}-1\right)$

5) $\left(-2 r^{2}+7 r s+4 s^{2}\right)+\left(-9 r^{2}+7 r s-2 s^{2}\right)$

Answer

$-11 r^{2}+14 r s+2 s^{2}$

6) $\left(-2 r^{2}+3 r t-4 t^{2}\right)+\left(7 r^{2}+4 r t-7 t^{2}\right)$

7) $\left(-8 y^{3}-3 y^{2} z-6 z^{3}\right)+\left(-3 y^{3}+7 y^{2} z-9 y z^{2}\right)$

Answer

$-11 y^{3}+4 y^{2} z-9 y z^{2}-6 z^{3}$

8) $\left(7 y^{2} z+8 y z^{2}+2 z^{3}\right)+\left(8 y^{3}-8 y^{2} z+9 y z^{2}\right)$

In Exercises 9-14, simplify the given expression by distributing the minus sign.

9) $-\left(5 x^{2}-4\right)$

Answer

$-5 x^{2}+4$

10) $-\left(-8 x^{2}-5\right)$

11) $-\left(9 r^{3}-4 r^{2} t-3 r t^{2}+4 t^{3}\right)$

Answer

$-9 r^{3}+4 r^{2} t+3 r t^{2}-4 t^{3}$

12) $-\left(7 u^{3}-8 u^{2} v+6 u v^{2}+5 v^{3}\right)$

13) $-\left(-5 x^{2}+9 x y+6 y^{2}\right)$

Answer

$5 x^{2}-9 x y-6 y^{2}$

14) $-\left(-4 u^{2}-6 u v+5 v^{2}\right)$

In Exercises 15-22, simplify the given expression. Arrange your answer in some sort of reasonable order.

15) $\left(-u^{3}-4 u^{2} w+7 w^{3}\right)-\left(u^{2} w+u w^{2}+3 w^{3}\right)$

Answer

$-u^{3}-5 u^{2} w-u w^{2}+4 w^{3}$

16) $\left(-b^{2} c+8 b c^{2}+8 c^{3}\right)-\left(6 b^{3}+b^{2} c-4 b c^{2}\right)$

17) $\left(2 y^{3}-2 y^{2} z+3 z^{3}\right)-\left(-8 y^{3}+5 y z^{2}-3 z^{3}\right)$

Answer

$10 y^{3}-2 y^{2} z-5 y z^{2}+6 z^{3}$

18) $\left(4 a^{3}+6 a c^{2}+5 c^{3}\right)-\left(2 a^{3}+8 a^{2} c-7 a c^{2}\right)$

19) $\left(-7 r^{2}-9 r s-2 s^{2}\right)-\left(-8 r^{2}-7 r s+9 s^{2}\right)$

Answer

$r^{2}-2 r s-11 s^{2}$

20) $\left(-4 a^{2}+5 a b-2 b^{2}\right)-\left(-8 a^{2}+7 a b+2 b^{2}\right)$

21) $\left(10 x^{2}+2 x-6\right)-\left(-8 x^{2}+14 x+17\right)$

Answer

$18 x^{2}-12 x-23$

22) $\left(-5 x^{2}+19 x-5\right)-\left(-15 x^{2}+19 x+8\right)$

In Exercises 23-28, for the given polynomial functions $f(x)$ and $g(x)$, simplify $f(x)+g(x)$. Arrange your answer in descending powers of $x$.

23) $\begin{aligned}f(x)&=-2 x^{2}+9 x+7 \\ g(x)&=8 x^{3}-7 x^{2}+5\end{aligned}$

Answer

$8 x^{3}-9 x^{2}+9 x+12$

24) $\begin{aligned}f(x)&=-8 x^{3}+6 x-9 \\ g(x)&=x^{3}-x^{2}+3 x\end{aligned}$

25) $\begin{aligned}f(x)&=5 x^{3}-5 x^{2}+8 x \\ g(x)&=7 x^{2}-2 x-9\end{aligned}$

Answer

$5 x^{3}+2 x^{2}+6 x-9$

26) $\begin{aligned}f(x)&=-x^{2}+8 x+1 \\ g(x)&=-7 x^{3}+8 x-9\end{aligned}$

27) $\begin{aligned}f(x)&=-3 x^{2}-8 x-9 \\ g(x)&=5 x^{2}-4 x+4\end{aligned}$

Answer

$2 x^{2}-12 x-5$

28) $\begin{aligned}f(x)&=-3 x^{2}+x-8 \\ g(x)&=7 x^{2}-9\end{aligned}$

In Exercises 29-34, for the given polynomial functions $f(x)$ and $g(x)$, simplify $f(x)−g(x)$. Arrange your answer in descending powers of $x$.

29) $\begin{aligned}f(x)&=-6 x^{3}-7 x+7 \\ g(x)&=-3 x^{3}-3 x^{2}-8 x\end{aligned}$

Answer

$-3 x^{3}+3 x^{2}+x+7$

30) $\begin{aligned}f(x)&=5 x^{3}-5 x+4 \\ g(x)&=-8 x^{3}-2 x^{2}-3 x\end{aligned}$

31) $\begin{aligned}f(x)&=12 x^{2}-5 x+4 \\ g(x)&=8 x^{2}-16 x-7\end{aligned}$

Answer

$4 x^{2}+11 x+11$

32) $\begin{aligned}f(x)&=-7 x^{2}+12 x+17 \\ g(x)&=-10 x^{2}-17\end{aligned}$

33) $\begin{aligned}f(x)&=-3 x^{3}-4 x+2 \\ g(x)&=-4 x^{3}-7 x^{2}+6\end{aligned}$

Answer

$x^{3}+7 x^{2}-4 x-4$

34) $\begin{aligned}f(x)&=-9 x^{2}+9 x+3 \\ g(x)&=7 x^{3}+7 x^{2}+5\end{aligned}$

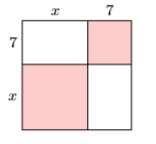
In Exercises 35-36, find the area of the given square by summing the areas of its four parts.

35)

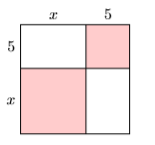
Answer

$x^{2}+10 x+25$

36)

37) Rachel runs a small business selling wicker baskets. Her business costs for producing and selling x wicker baskets are given by the polynomial function $C(x) = 232+ 7x−0.0085x^2$. The revenue she earns from selling x wicker baskets is given by the polynomial function $R(x) = 33.45x$. Find a formula for $P(x)$, the profit made from selling $x$ wicker baskets. Use your formula to determine Rachel’s profit if she sells $233$ wicker baskets. Round your answer to the nearest cent.

Answer

$\$6,392.31$

38) Eloise runs a small business selling baby cribs. Her business costs for producing and selling $x$ baby cribs are given by the polynomial function $C(x) = 122 + 8x − 0.0055x^2$. The revenue she earns from selling $x$ baby cribs is given by the polynomial function $R(x) = 33.45x$. Find a formula for $P(x)$, the profit made from selling $x$ baby cribs. Use your formula to determine Eloise’s profit if she sells $182$ baby cribs. Round your answer to the nearest cent.

5.5: Laws of Exponents

In Exercises 1-8, simplify each of the given exponential expressions.

1) $(-4)^{3}$

Answer

$-64$

2) $(-9)^{2}$

3) $\left(-\dfrac{5}{7}\right)^{0}$

Answer

$1$

4) $\left(-\dfrac{2}{5}\right)^{0}$

5) $\left(-\dfrac{4}{3}\right)^{2}$

Answer

$\dfrac{16}{9}$

6) $\left(-\dfrac{2}{3}\right)^{2}$

7) $(-19)^{0}$

Answer

$1$

8) $(-17)^{0}$

In Exercises 9-18, simplify each of the given exponential expressions.

9) $(7 v-6 w)^{18} \cdot(7 v-6 w)^{17}$

Answer

$(7 v-6 w)^{35}$

10) $(8 a+7 c)^{3} \cdot(8 a+7 c)^{19}$

11) $3^{4} \cdot 3^{0}$

Answer

$3^{4}$

12) $5^{7} \cdot 5^{0}$

13) $4^{n} \cdot 4^{8 n+3}$

Answer

$4^{9 n+3}$

14) $4^{6 m+5} \cdot 4^{m-5}$

15) $x^{8} \cdot x^{3}$

Answer

$x^{11}$

16) $a^{9} \cdot a^{15}$

17) $2^{5} \cdot 2^{3}$

Answer

$2^{8}$

18) $2^{10} \cdot 2^{3}$

In Exercises 19-28, simplify each of the given exponential expressions.

19) $\dfrac{4^{16}}{4^{16}}$

Answer

$1$

20) $\dfrac{3^{12}}{3^{12}}$

21) $\dfrac{w^{11}}{w^{7}}$

Answer

$w^{4}$

22) $\dfrac{c^{10}}{c^{8}}$

23) $\dfrac{(9 a-8 c)^{15}}{(9 a-8 c)^{8}}$

Answer

$(9 a-8 c)^{7}$

24) $\dfrac{(4 b+7 c)^{15}}{(4 b+7 c)^{5}}$

25) $\dfrac{2^{9 n+5}}{2^{3 n-4}}$

Answer

$2^{6 n+9}$

26) $\dfrac{2^{4 k-9}}{2^{3 k-8}}$

27) $\dfrac{4^{17}}{4^{9}}$

Answer

$4^{8}$

28) $\dfrac{2^{17}}{2^{6}}$

In Exercises 29-38, simplify each of the given exponential expressions.

29) $\left(4^{8 m-6}\right)^{7}$

Answer

$4^{56 m-42}$

30) $\left(2^{2 m-9}\right)^{3}$

31) $\left[(9 x+5 y)^{3}\right]^{7}$

Answer

$(9 x+5 y)^{21}$

32) $\left[(4 u-v)^{8}\right]^{9}$

33) $\left(4^{3}\right)^{2}$

Answer

$4^{6}$

34) $\left(3^{4}\right)^{2}$

35) $\left(c^{4}\right)^{7}$

Answer

$c^{28}$

36) $\left(w^{9}\right)^{5}$

37) $\left(6^{2}\right)^{0}$

Answer

$1$

38) $\left(8^{9}\right)^{0}$

In Exercises 39-48, simplify each of the given exponential expressions.

39) $(u w)^{5}$

Answer

$u^{5} w^{5}$

40) $(a c)^{4}$

41) $(-2 y)^{3}$

Answer

$-8 y^{3}$

42) $(-2 b)^{3}$

43) $\left(3 w^{9}\right)^{4}$

Answer

$81 w^{36}$

44) $\left(-3 u^{9}\right)^{4}$

45) $\left(-3 x^{8} y^{2}\right)^{4}$

Answer

$81 x^{32} y^{8}$

46) $\left(2 x^{8} z^{6}\right)^{4}$

47) $\left(7 s^{6 n}\right)^{3}$

Answer

$343 s^{18 n}$

48) $\left(9 b^{6 n}\right)^{3}$

In Exercises 49-56, simplify each of the given exponential expressions.

49) $\left(\dfrac{v}{2}\right)^{3}$

Answer

$\dfrac{v^{3}}{8}$

50) $\left(\dfrac{t}{9}\right)^{2}$

51) $\left(-\dfrac{2}{u}\right)^{2}$

Answer

$\dfrac{4}{u^{2}}$

52) $\left(-\dfrac{3}{w}\right)^{3}$

53) $\left(-\dfrac{r^{8}}{5}\right)^{4}$

Answer

$\dfrac{r^{32}}{625}$

54) $\left(-\dfrac{x^{11}}{5}\right)^{5}$

55) $\left(\dfrac{5}{c^{9}}\right)^{4}$

Answer

$\dfrac{625}{c^{36}}$

56) $\left(\dfrac{5}{u^{12}}\right)^{2}$

57) Complete each of the laws of exponents presented in the first column, then use the results to simplify the expressions in the second column.

$a^{m} a^{n}=?$	$a^{3} a^{5}=?$
$\dfrac{a^{m}}{a^{n}}=?$	$\dfrac{a^{6}}{a^{2}}=?$
$\left(a^{m}\right)^{n}=?$	$\left(a^{5}\right)^{7}=?$
$(a b)^{m}=?$	$(a b)^{9}=?$
$\left(\dfrac{a}{b}\right)^{m}=?$	$\left(\dfrac{a}{b}\right)^{3}=?$

Answer

The general answers are: $a^{m+n}, a^{m-n}, a^{m n}, a^{m} b^{m}, \dfrac{a^m}{b^m}$.

The specific answers are: $a^{8}, a^{4}, a^{35}, a^{9} b^{9}, \dfrac{a^3}{b^3}$.

5.6: Multiplying Polynomials

In Exercises 1-10, simplify the given expression.

1) $-3(7 r)$

Answer

$-21 r$

2) $7(3 a)$

3) $\left(-9 b^{3}\right)\left(-8 b^{6}\right)$

Answer

$72b^{9}$

4) $\left(8 s^{3}\right)\left(-7 s^{4}\right)$

5) $\left(-7 r^{2} t^{4}\right)\left(7 r^{5} t^{2}\right)$

Answer

$-49 r^{7} t^{6}$

6) $\left(-10 s^{2} t^{8}\right)\left(-7 s^{4} t^{3}\right)$

7) $\left(-5 b^{2} c^{9}\right)\left(-8 b^{4} c^{4}\right)$

Answer

$40 b^{6} c^{13}$

8) $\left(-9 s^{2} t^{8}\right)\left(7 s^{5} t^{4}\right)$

9) $\left(-8 v^{3}\right)\left(4 v^{4}\right)$

Answer

$-32 v^{7}$

10) $\left(-9 y^{3}\right)\left(3 y^{5}\right)$

In Exercises 11-22, use the distributive property to expand the given expression.

11) $9\left(-2 b^{2}+2 b+9\right)$

Answer

$-18 b^{2}+18 b+81$

12) $9\left(-4 b^{2}+7 b-8\right)$

13) $-4\left(10 t^{2}-7 t-6\right)$

Answer

$-40 t^{2}+28 t+24$

14) $-5\left(-7 u^{2}-7 u+2\right)$

15) $-8 u^{2}\left(-7 u^{3}-8 u^{2}-2 u+10\right)$

Answer

$56 u^{5}+64 u^{4}+16 u^{3}-80 u^{2}$

16) $-3 s^{2}\left(-7 s^{3}-9 s^{2}+6 s+3\right)$

17) $10 s^{2}\left(-10 s^{3}+2 s^{2}+2 s+8\right)$

Answer

$-100 s^{5}+20 s^{4}+20 s^{3}+80 s^{2}$

18) $8 u^{2}\left(9 u^{3}-5 u^{2}-2 u+5\right)$

19) $2 s t\left(-4 s^{2}+8 s t-10 t^{2}\right)$

Answer

$-8 s^{3} t+16 s^{2} t^{2}-20 s t^{3}$

20) $7 u v\left(-9 u^{2}-3 u v+4 v^{2}\right)$

21) $-2 u w\left(10 u^{2}-7 u w-2 w^{2}\right)$

Answer

$-20 u^{3} w+14 u^{2} w^{2}+4 u w^{3}$

22) $-6 v w\left(-5 v^{2}+9 v w+5 w^{2}\right)$

In Exercises 23-30, use the technique demonstrated in Example 5.6.8 and Example 5.6.9 to expand each of the following expressions using the distributive property.

23) $(-9 x-4)(-3 x+2)$

Answer

$27 x^{2}-6 x-8$

24) $(4 x-10)(-2 x-6)$

25) $(3 x+8)(3 x-2)$

Answer

$9 x^{2}+18 x-16$

26) $(-6 x+8)(-x+1)$

27) $-12 x^{3}+14 x^{2}+6 x-5$

Answer

$-\dfrac{930}{289}$

28) $(4 x-6)\left(-7 x^{2}-10 x+10\right)$

29) $(x-6)\left(-2 x^{2}-4 x-4\right)$

Answer

$-2 x^{3}+8 x^{2}+20 x+24$

30) $(5 x-10)\left(-3 x^{2}+7 x-8\right)$

In Exercises 31-50, use the shortcut technique demonstrated in Example 5.6.10, Example 5.6.11, and Example 5.6.12 to expand each of the following expressions using the distributive property.

31) $(8 u-9 w)(8 u-9 w)$

Answer

$64 u^{2}-144 u w+81 w^{2}$

32) $(3 b+4 c)(-8 b+10 c)$

33) $(9 r-7 t)(3 r-9 t)$

Answer

$27 r^{2}-102 r t+63 t^{2}$

34) $(-6 x-3 y)(-6 x+9 y)$

35) $(4 r-10 s)\left(-10 r^{2}+10 r s-7 s^{2}\right)$

Answer

$-40 r^{3}+140 r^{2} s-128 r s^{2}+70 s^{3}$

36) $(5 s-9 t)\left(-3 s^{2}+4 s t-9 t^{2}\right)$

37) $(9 x-2 z)\left(4 x^{2}-4 x z-10 z^{2}\right)$

Answer

$36 x^{3}-44 x^{2} z-82 x z^{2}+20 z^{3}$

38) $(r-4 t)\left(7 r^{2}+4 r t-2 t^{2}\right)$

39) $(9 r+3 t)^{2}$

Answer

$81 r^{2}+54 r t+9 t^{2}$

40) $(4 x+8 z)^{2}$

41) $(4 y+5 z)(4 y-5 z)$

Answer

$16 y^{2}-25 z^{2}$

42) $(7 v+2 w)(7 v-2 w)$

43) $(7 u+8 v)(7 u-8 v)$

Answer

$49 u^{2}-64 v^{2}$

44) $(6 b+8 c)(6 b-8 c)$

45) $(7 b+8 c)^{2}$

Answer

$49 b^{2}+112 b c+64 c^{2}$

46) $(2 b+9 c)^{2}$

47) $\left(2 t^{2}+9 t+4\right)\left(2 t^{2}+9 t+4\right)$

Answer

$4 t^{4}+36 t^{3}+97 t^{2}+72 t+16$

48) $\left(3 a^{2}-9 a+4\right)\left(3 a^{2}-9 a+2\right)$

49) $\left(4 w^{2}+3 w+5\right)\left(3 w^{2}-6 w+8\right)$

Answer

$12 w^{4}-15 w^{3}+29 w^{2}-6 w+40$

50) $\left(4 s^{2}+3 s+8\right)\left(2 s^{2}+4 s-9\right)$

51) The demand for widgets is given by the function $x = 320−0.95p$, where $x$ is the demand and $p$ is the unit price. What unit price should a retailer charge for widgets in order that his revenue from sales equals $\$7,804$? Round your answers to the nearest cent.

Answer

$\$ 26.47$, $\$ 310.37$

52) The demand for widgets is given by the function $x = 289−0.91p$, where $x$ is the demand and $p$ is the unit price. What unit price should a retailer charge for widgets in order that his revenue from sales equals $\$7,257$? Round your answers to the nearest cent.

53) In the image that follows, the edge of the outer square is $6$ inches longer than $3$ times the edge of the inner square.

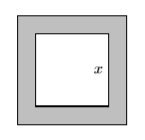
1. Express the area of the shaded region as a polynomial in terms of $x$, the edge of the inner square. Your final answer must be presented as a second degree polynomial in the form $A(x)=ax^2 + bx + c$.
2. Given that the edge of the inner square is $5$ inches, use the polynomial in part (a) to determine the area of the shaded region.

Answer

$A(x)=8 x^{2}+36 x+36$, $A(5)=416$ square inches

54) In the image that follows, the edge of the outer square is $3$ inches longer than $2$ times the edge of the inner square.

1. Express the area of the shaded region as a polynomial in terms of $x$, the edge of the inner square. Your final answer must be presented as a second degree polynomial in the form $A(x)=ax^2 + bx + c$.
2. Given that the edge of the inner square is $4$ inches, use the polynomial in part (a) to determine the area of the shaded region.

55) A rectangular garden is surrounded by a uniform border of lawn measuring $x$ units wide. The entire rectangular plot measures $31$ by $29$ feet.

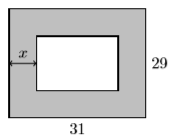
1. Find the area of the interior rectangular garden as a polynomial in terms of $x$. Your final answer must be presented as a second degree polynomial in the form $A(x)=ax^2 + bx + c$.
2. Given that the width of the border is $9.3$ feet, use the polynomial in part (a) to determine the area of the interior rectangular garden.

Answer

$899-120 x+4 x^{2}$, $128.96$ square feet

56) A rectangular garden is surrounded by a uniform border of lawn measuring $x$ units wide. The entire rectangular plot measures $35$ by $24$ feet.

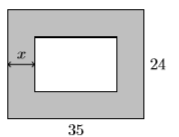
1. Find the area of the interior rectangular garden as a polynomial in terms of $x$. Your final answer must be presented as a second degree polynomial in the form $A(x)=ax^2 + bx + c$.
2. Given that the width of the border is $1.5$ feet, use the polynomial in part (a) to determine the area of the interior rectangular garden.

5.7: Special Products

In Exercises 1-12, use the FOIL shortcut as in Example 5.7.3 and Example 5.7.4 to multiply the given binomials.

1) $(5 x+2)(3 x+4)$

Answer

$15 x^{2}+26 x+8$

2) $(5 x+2)(4 x+3)$

3) $(6 x-3)(5 x+4)$

Answer

$30 x^{2}+9 x-12$

4) $(6 x-2)(4 x+5)$

5) $(5 x-6)(3 x-4)$

Answer

$15 x^{2}-38 x+24$

6) $(6 x-4)(3 x-2)$

7) $(6 x-2)(3 x-5)$

Answer

$18 x^{2}-36 x+10$

8) $(2 x-3)(6 x-4)$

9) $(6 x+4)(3 x+5)$

Answer

$18 x^{2}+42 x+20$

10) $(3 x+2)(4 x+6)$

11) $(4 x-5)(6 x+3)$

Answer

$24 x^{2}-18 x-15$

12) $(3 x-5)(2 x+6)$

In Exercises 13-20, use the difference of squares shortcut as in Example 5.7.5 to multiply the given binomials.

13) $(10 x-12)(10 x+12)$

Answer

$100 x^{2}-144$

14) $(10 x-11)(10 x+11)$

15) $(6 x+9)(6 x-9)$

Answer

$36 x^{2}-81$

16) $(9 x+2)(9 x-2)$

17) $(3 x+10)(3 x-10)$

Answer

$9 x^{2}-100$

18) $(12 x+12)(12 x-12)$

19) $(10 x-9)(10 x+9)$

Answer

$100 x^{2}-81$

20) $(4 x-6)(4 x+6)$

In Exercises 21-28, use the squaring a binomial shortcut as in Example 5.7.8 to expand the given expression.

21) $(2 x+3)^{2}$

Answer

$4 x^{2}+12 x+9$

22) $(8 x+9)^{2}$

23) $(9 x-8)^{2}$

Answer

$81 x^{2}-144 x+64$

24) $(4 x-5)^{2}$

25) $(7 x+2)^{2}$

Answer

$49 x^{2}+28 x+4$

26) $(4 x+2)^{2}$

27) $(6 x-5)^{2}$

Answer

$36 x^{2}-60 x+25$

28) $(4 x-3)^{2}$

In Exercises 29-76, use the appropriate shortcut to multiply the given binomials.

29) $(11 x-2)(11 x+2)$

Answer

$121 x^{2}-4$

30) $(6 x-7)(6 x+7)$

31) $(7 r-5 t)^{2}$

Answer

$49 r^{2}-70 r t+25 t^{2}$

32) $(11 u-9 w)^{2}$

33) $(5 b+6 c)(3 b-2 c)$

Answer

$15 b^{2}+8 b c-12 c^{2}$

34) $(3 r+2 t)(5 r-3 t)$

35) $(3 u+5 v)(3 v-5 v)$

Answer

$9 u^{2}-25 v^{2}$

36) $(11 a+4 c)(11 a-4 c)$

37) $\left(9 b^{3}+10 c^{5}\right)\left(9 b^{3}-10 c^{5}\right)$

Answer

$81 b^{6}-100 c^{10}$

38) $\left(9 r^{5}+7 t^{2}\right)\left(9 r^{5}-7 t^{2}\right)$

39) $(9 s-4 t)(9 s+4 t)$

Answer

$81 s^{2}-16 t^{2}$

40) $(12 x-7 y)(12 x+7 y)$

41) $(7 x-9 y)(7 x+9 y)$

Answer

$49 x^{2}-81 y^{2}$

42) $(10 r-11 t)(10 r+11 t)$

43) $(6 a-6 b)(2 a+3 b)$

Answer

$12 a^{2}+6 a b-18 b^{2}$

44) $(6 r-5 t)(2 r+3 t)$

45) $(10 x-10)(10 x+10)$

Answer

$100 x^{2}-100$

46) $(12 x-8)(12 x+8)$

47) $(4 a+2 b)(6 a-3 b)$

Answer

$24 a^{2}-6 b^{2}$

48) $(3 b+6 c)(2 b-4 c)$

49) $(5 b-4 c)(3 b+2 c)$

Answer

$15 b^{2}-2 b c-8 c^{2}$

50) $(3 b-2 c)(4 b+5 c)$

51) $(4 b-6 c)(6 b-2 c)$

Answer

$24 b^{2}-44 b c+12 c^{2}$

52) $(4 y-4 z)(5 y-3 z)$

53) $\left(11 r^{5}+9 t^{2}\right)^{2}$

Answer

$121 r^{10}+198 r^{5} t^{2}+81 t^{4}$

54) $\left(11 x^{3}+10 z^{5}\right)^{2}$

55) $(4 u-4 v)(2 u-6 v)$

Answer

$8 u^{2}-32 u v+24 v^{2}$

56) $(4 u-5 w)(5 u-6 w)$

57) $\left(8 r^{4}+7 t^{5}\right)^{2}$

Answer

$64 r^{8}+112 r^{4} t^{5}+49 t^{10}$

58) $\left(2 x^{5}+5 y^{2}\right)^{2}$

59) $(4 r+3 t)(4 r-3 t)$

Answer

$16 r^{2}-9 t^{2}$

60) $(3 r+4 s)(3 r-4 s)$

61) $(5 r+6 t)^{2}$

Answer

$25 r^{2}+60 r t+36 t^{2}$

62) $(12 v+5 w)^{2}$

63) $(3 x-4)(2 x+5)$

Answer

$6 x^{2}+7 x-20$

64) $(5 x-6)(4 x+2)$

65) $(6 b+4 c)(2 b+3 c)$

Answer

$12 b^{2}+26 b c+12 c^{2}$

66) $(3 v+6 w)(2 v+4 w)$

67) $\left(11 u^{2}+8 w^{3}\right)\left(11 u^{2}-8 w^{3}\right)$

Answer

$121 u^{4}-64 w^{6}$

68) $\left(3 u^{3}+11 w^{4}\right)\left(3 u^{3}-11 w^{4}\right)$

69) $(4 y+3 z)^{2}$

Answer

$16 y^{2}+24 y z+9 z^{2}$

70) $(11 b+3 c)^{2}$

71) $(7 u-2 v)^{2}$

Answer

$49 u^{2}-28 u v+4 v^{2}$

72) $(4 b-5 c)^{2}$

73) $(3 v+2 w)(5 v+6 w)$

Answer

$15 v^{2}+28 v w+12 w^{2}$

74) $(5 y+3 z)(4 y+2 z)$

75) $(5 x-3)(6 x+2)$

Answer

$30 x^{2}-8 x-6$

76) $(6 x-5)(3 x+2)$

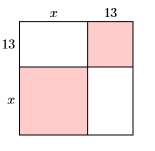
For each of the following figure, compute the area of the square using two methods.

1. Find the area by summing the areas of its parts (see Example 5.5.7).
2. Find the area by squaring the side of the square using the squaring a binomial shortcut.

77)

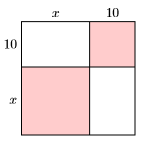
Answer

$A=x^{2}+20 x+100$

78)

79) A square piece of cardboard measures $12$ inches on each side. Four squares, each having a side of $x$ inches, are cut and removed from each of the four corners of the square piece of cardboard. The sides are then folded up along the dashed lines to form a box with no top.

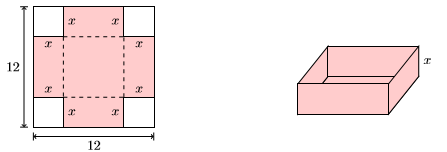
1. Find the volume of the box as a function of $x$, the measure of the side of each square cut from the four corner of the original piece of cardboard. Multiply to place your answer in standard polynomial form, simplifying your answer as much as possible.
2. Use the resulting polynomial to determine the volume of the box if squares of length $1.25$ inches are cut from each corner of the original piece of cardboard. Round your answer to the nearest cubic inch.

Answer

1. $V(x)=144 x-48 x^{2}+4 x^{3}$
2. $V(1.25) \approx 113$ cubic inches

80) Consider again the box formed in Exercise 79.

1. Find the surface area of the box as a function of $x$, the measure of the side of each square cut from the four corner of the original piece of cardboard. Multiply to place your answer in standard polynomial form, simplifying your answer as much as possible.
2. Use the resulting polynomial to determine the surface area of the box if squares of length $1.25$ inches are cut from each corner of the original piece of cardboard. Round your answer to the nearest square inch.