7.1: Negative Exponents

Last updated

Feb 21, 2022
Save as PDF
- 7: Rational Expressions
- 7.2: Scientiﬁc Notation

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

We begin with a seemingly silly but powerful definition on what it means to raise a number to a power of $−1$ .

Raising to a Power of $−1$

To raise an object to a power of $−1$ , simply invert the object (turn it upside down).

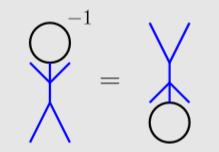
$fig 7.1.a.png$

More formally, inverting a number is known as taking its reciprocal.

Example $\PageIndex{1}$

Simplify each of the following expressions:

$4^{-1}$
$\left ( \dfrac{2}{3} \right )^{-1}$
$-\left ( \dfrac{3}{5} \right )^{-1}$

Solution

In each case, we simply invert the given number.

$\left ( \dfrac{2}{3} \right )^{-1} = \dfrac{3}{2}$
$-\left ( \dfrac{3}{5} \right )^{-1} = -\dfrac{5}{3}$

Exercise $\PageIndex{1}$

Simplify: $\left ( \dfrac{7}{4} \right )^{-1}$

Answer: $\dfrac{4}{7}$

You might be asking “Why does raising to the power of minus one invert the number?” To answer this question, recall the product of a number and its reciprocal is one. For example,

$4\cdot \dfrac{1}{4} = 1 \label{Eq7.1.1}$

Next, consider what happens when we multiply $4^1$ and $4^{−1}$ . If we apply the usual law of exponents (assuming they work for both positive and negative exponents), we would add the exponents ( $1 + (−1) = 0$ ).

$4^1\cdot 4^{-1} = 4^0 \label{Eq7.1.2}$

However, because $4^1 = 4$ and $4^0 = 1$ , this last equation is equivalent to:

$4\cdot 4^{-1} = 1 \label{Eq7.1.3}$

When you compare Equation $\ref{Eq7.1.1}$ and $\ref{Eq7.1.3}$ , it is clear that $4^{−1}$ and $1/4$ are both reciprocals of the number $4$ . Because reciprocals are unique, $4^{-1} = \dfrac{1}{4}$ .

In similar fashion, one can discover the meaning of $a^{−n}$ . Start with the fact that multiplying reciprocals yields an answer of one.

$a^n\cdot \dfrac{1}{a^n} = 1 \label{Eq7.1.4}$

If we multiply $a^n$ and $a^{−n}$ , we add the exponents as follows.

$a^n\cdot a^{−n} = a^0 \nonumber$

Providing $a\neq = 0$ , then $a^0 = 1$ , so we can write

$a^n\cdot a^{-n} = 1 \label{Eq7.1.5}$

Comparing Equations $\ref{Eq7.1.4}$ and $\ref{Eq7.1.5}$ , we note that both $1/a^n$ and $a^{−n}$ are reciprocals of $a^n$ . Because every number has a unique reciprocal, $a^{−n}$ and $1/a^n$ are equal.

Raising to a negative integer

Provided a\neq= 0,

$a^{-n} = \dfrac{1}{a^n} \nonumber$

Example $\PageIndex{2}$

Simplify each of the following expressions:

$2^{-3}$
$(-5)^{-2}$
$(-4)^{-3}$

Solution

In each example, we use the property $a^{−n} =1/a^n$ to simplify the given expression.

$\begin{align*} 2^{-3} &= \dfrac{1}{2^3}\\ &= \dfrac{1}{8} \end{align*}$
$\begin{align*} (-5)^{-2} &= \dfrac{1}{(-5)^2}\\ &= \dfrac{1}{25} \end{align*}$
$\begin{align*} (-4)^{-3} &= \dfrac{1}{(-4)^3}\\ &= -\dfrac{1}{64} \end{align*}$

In Raising to a Negative Integer, we’ll address how you can perform each of the above computations mentally.

Exercise $\PageIndex{2}$

Simplify: $3^{-2}$

Answer: $\dfrac{1}{9}$

Laws of Exponents

In the arguments demonstrating that $4^{−1} =1 /4$ and $a^{−n} =1/a^n$ , we appealed to one of the laws of exponents learned in Chapter 5, Section 5. Fortunately, the laws of exponents work exactly the same whether the exponents are positive or negative integers.

Laws of Exponents

If $m$ and $n$ are integers, then:

$a^ma^n = a^{m+n}$
$\dfrac{a^m}{a^n} = a^{m-n}$
$(a^m)^n = a^{mn}$
$(ab)^n = a^nb^n$
$\left (\dfrac{a}{b} \right )^n = \dfrac{a^n}{a^n}$

Example $\PageIndex{3}$

Simplify each of the following expressions:

$y^5y^{−7}$
$2^{−2}\cdot 2^{−3}$
$x^{−4}x^6$

Solution

In each case, we use the first law of exponents ( $a^ma^n = a^{m+n}$ ). Because we are multiplying like bases, we repeat the base and add the exponents.

$\begin{align*} y^5y^{-7} &= y^{5+(-7)}\\ &= y^{-2} \end{align*}$
$\begin{align*} 2^{-2}\cdot 2^{-3} &= 2^{-2+(-3)}\\ &= 2^{-5} \end{align*}$
$\begin{align*} x^{-4}x^{6} &= x^{-4+6}\\ &= x^2 \end{align*}$

Exercise $\PageIndex{3}$

Simplify: $t^8\cdot t^{−4}$

Answer: $t^4$

Example $\PageIndex{4}$

Simplify each of the following expressions:

$\dfrac{x^4}{x^7}$
$\dfrac{3^{-4}}{3^5}$
$\dfrac{z^{-3}}{z^{-5}}$

Solution

In each case, we use the second law of exponents ( $a^m/a^n = a^{m−n}$ ). Because we are dividing like bases, we repeat the base and subtract the exponents. Recall that subtraction means “add the opposite.”

$\begin{align*} \dfrac{x^4}{x^7} &= x^{4-7}\\ &= x^{4+(-7)}\\ &= x^{-3} \end{align*}$
$\begin{align*} \dfrac{3^{-4}}{3^5} &= 3^{-4-5}\\ &= 3^{-4+(-5)}\\ &= 3^{-9} \end{align*}$
$\begin{align*} \dfrac{z^{-3}}{z^{-5}} &= z^{-3-(-5)}\\ &= z^{-3+5}\\ &= z^{2} \end{align*}$

Exercise $\PageIndex{4}$

Simplify: $\dfrac{y^{-6}}{y^{-2}}$

Answer: $y^{-4}$

Example $\PageIndex{5}$

Simplify each of the following expressions:

$(5^{−2})^3$
$(a^{−3})^{−4}$
$(w^2)^{−7}$

Solution

In each case, we are using the third law of exponents ( $(a^m)^n = a^{mn}$ ). Because we are raising a power to another power, we repeat the base and multiply the exponents.

$\begin{align*} (5^{-2})^3 &= 5^{(-2)(3)}\\ &= 5^{-6} \end{align*}$
$\begin{align*} (a^{-3})^{-4} &= a^{(-3)(-4)}\\ &= a^{12} \end{align*}$
$\begin{align*} (w^2)^{-7} &= w^{(2)(-7)}\\ &= w^{-14} \end{align*}$

Exercise $\PageIndex{5}$

Simplify: $(z^5)^{−2}$

Answer: $z^{-10)$

Raising to a Negative Integer

We know what happens when you raise a number to $−1$ , you invert the number or turn it upside down. But what happens when you raise a number to a negative integer other than negative one?

As an example, consider the expression $3^{−2}$ . Using the third law of exponents ( $(a^m)^n = a^{mn}$ ), we can write this expression in two equivalent forms.

Note that $3^{−2}$ is equivalent to $(3^2)^{−1}$ . They are equivalent because the third law of exponents instructs us to multiply the exponents when raising a power to another power. Finally, note that to evaluate $(3^2)^{−1}$ , we first square, then invert the result. $\begin{align*} 3^{-2} &= (3^2)^{-1} \quad \color {Red} \text {Repeat base and multiply exponents.}\\ &= 9^{-1} \quad \color {Red} \text {Simplify: } 3^2=9\\ &= \dfrac{1}{9} \quad \color {Red} \text {Simplify: } 9^{-1}=1/9 \end{align*} \nonumber$
Note that $3^{−2}$ is also equivalent to $(3^{−1})^2$ . They are equivalent because the third law of exponents instructs us to multiply the exponents when raising a power to another power. Finally, note that to evaluate $(3^{−1})^2$ , we first invert, then square the result. $\begin{align*} 3^{-2} &= (3^{-1})^2 \quad \color {Red} \text {Repeat base and multiply exponents.}\\ &= \left (\dfrac{1}{3} \right )^2 \quad \color {Red} \text {Simplify: } 3^{-1}=1/3\\ &= \dfrac{1}{9} \quad \color {Red} \text {Simplify: } (1/3)^{2}=1/9 \end{align*} \nonumber$

Using either technique, $3^{−2} =1/9$ . You can either square and invert, or you can invert and square. In each case, the $2$ means “square” and the minus sign means “invert,” and this example shows that it doesn’t matter which you do first.

Example $\PageIndex{6}$

Simplify each of the following expressions:

$5^{−3}$
$(−4)^{−2}$
$\left (\dfrac{3}{5} \right )^{-2}$
$\left (-\dfrac{2}{3} \right )^{-3}$

Solution

We’ll cube then invert. $\begin{align*} 5^{-3} &= (5^3)^{-1} \quad \color {Red} \text {Repeat base and multiply exponents.}\\ &= 125^{-1} \quad \color {Red} \text {Simplify: } 5^{3}=125\\ &= \dfrac{1}{125} \quad \color {Red} \text {Invert: } 125^{-1}=1/125 \end{align*} \nonumber$ Note that the three means “cube” and the minus sign means “invert,” so it is possible to do all of this work mentally: cube $5$ to get $125$ , then invert to get $1/125$ .
We’ll square then invert. $\begin{align*} (-4)^{-2} &= ((-4)^2)^{-1} \quad \color {Red} \text {Repeat base and multiply exponents.}\\ &= 16^{-1} \quad \color {Red} \text {Simplify: } (-4)^{2}=16\\ &= \dfrac{1}{16} \quad \color {Red} \text {Invert: } 16^{-1}=1/16 \end{align*} \nonumber$ Note that the two means “square” and the minus sign means “invert,” so it is possible to do all of this work mentally: square $−4$ to get $16$ , then invert to get $1/16$ .
Again, we’ll square then invert. $\begin{align*} \left (\dfrac{3}{5} \right )^{-2} &= \left ( \left (\dfrac{3}{5} \right )^{2} \right )^{-1} \quad \color {Red} \text {Repeat base and multiply exponents.}\\ &= \left (\dfrac{9}{25} \right )^{-1} \quad \color {Red} \text {Simplify: } (3/5)^{2}=9/25\\ &= \dfrac{25}{9} \quad \color {Red} \text {Invert: } (9/25)^{-1}=25/9 \end{align*} \nonumber$ Note that the two means “square” and the minus sign means “invert,” so it is possible to do all of this work mentally: square $3/5$ to get $9/25$ , then invert to get $25/9$ .
This time we’ll cube then invert. $\begin{align*} \left (-\dfrac{2}{3} \right )^{-3} &= \left ( \left (-\dfrac{2}{3} \right )^{3} \right )^{-1} \quad \color {Red} \text {Repeat base and multiply exponents.}\\ &= \left (-\dfrac{8}{27} \right )^{-1} \quad \color {Red} \text {Simplify: } (-2/3)^{2}=-8/27\\ &= -\dfrac{27}{8} \quad \color {Red} \text {Invert: } (-8/27)^{-1}=-27/8 \end{align*} \nonumber$ Note that the three means “cube” and the minus sign means “invert,” so it is possible to do all of this work mentally: cube $−2/3$ to get $−8/27$ , then invert to get $−27/8$ .

Exercise $\PageIndex{6}$

Simplify: $\left (\dfrac{5}{4} \right )^{-3}$

Answer: $\dfrac{64}{125}$

Applying the Laws of Exponents

In this section we’ll simplify a few more complicated expressions using the laws of exponents.

Example $\PageIndex{7}$

Simplify: $(2x^{−2}y^3)(−3x^5y^{−6})$

Solution

All the operators involved are multiplication, so the commutative and associative properties of multiplication allow us to change the order and grouping. We’ll show this regrouping here, but this step can be done mentally. $(2x−2y^3)(−3x^5y^{−6}) = [(2)(−3)](x^{−2}x^5)(y^3y^{−6}) \nonumber$ When multiplying, we repeat the base and add the exponents. $\begin{align*} &= -6x^{-2+5}y^{3+(-6)} \\ &= -6x^3y^{-3} \end{align*} \nonumber$ In the solution above, we’ve probably shown way too much work. It’s far easier to perform all of these steps mentally, multiplying the $2$ and the $−3$ , then repeating bases and adding exponents, as in: $(2x^{−2}y^3)(−3x^5y^{−6})=−6x^3y^{−3} \nonumber$

Exercise $\PageIndex{7}$

Simplify: $(−5x^8y^{−2})(−2x^{−6}y^{−1})$

Answer: $10x^2y^{−3}$

Example $\PageIndex{8}$

Simplify: $\dfrac{6x^{-2}y^5}{9x^3y^{-2}}$

Solution

The simplest approach is to first write the expression as a product.

$\dfrac{6x^{-2}y^5}{9x^3y^{-2}} = \dfrac{6}{9}\cdot \dfrac{x^{-2}}{x^3}\cdot \dfrac{y^5}{y^{-2}} \nonumber$

Reduce $6/9$ to lowest terms. Because we are dividing like bases, we repeat the base and subtract the exponents.

$\begin{align*} &= \dfrac{2}{3}x^{-2-3}y^{5-(-2)}\\ &= \dfrac{2}{3}x^{-2+(-3)}y^{5+2}\\ &= \dfrac{2}{3}x^{-5}y^{7} \end{align*} \nonumber$ In the solution above, we’ve probably shown way too much work. It’s far easier to imagine writing the expression as a product, reducing 6/9, then repeating bases and subtracting exponents, as in:

$\dfrac{6x^{-2}y^5}{9x^3y^{-2}} = \dfrac{2}{3}x^{-5}y^{7} \nonumber$

Exercise $\PageIndex{8}$

Simplify: $\dfrac{10x^{3}y^{-1}}{4x^{-2}y^{5}}$

Answer: $\dfrac{5}{2}x^{5}y^{-6}$

Example $\PageIndex{9}$

Simplify: $(2x^{−2}y^4)^{−3}$

Solution

The fourth law of exponents ( $(ab)^n = a^nb^n$ ) says that when you raise a product to a power, you must raise each factor to that power. So we begin by raising each factor to the minus three power.

$(2x^{−2}y^3)^{−3} =2^{−3}(x^{−2})^{−3}(y^4)^{−3} \nonumber$

To raise two to the minus three, we must cube two and invert: $2^{−3} =1 /8$ . Secondly, raising a power to a power requires that we repeat the base and multiply exponents.

$\begin{align*} &= \dfrac{1}{8}x^{(-2)(-3)}y^{(4)(-3)}\\ &= \dfrac{1}{8}x^{6}y^{-12} \end{align*} \nonumber$

In the solution above, we’ve probably shown way too much work. It’s far easier raise each factor to the minus three mentally: $2^{−3} =1 /8$ , then multiply each exponent on the remaining factors by $−3$ , as in

$(2x^{-2}y^4)^{-3} = \dfrac{1}{8}x^{6}y^{-12} \nonumber$

Exercise $\PageIndex{9}$

Simplify: $(3x^4y^{−3})^{−2}$

Answer: $\dfrac{1}{9}x^{-8}y^{6}$

Clearing Negative Exponents

Often, we’re asked to provide a final answer that is free of negative exponents. It is common to hear the instruction “no negative exponents in the final answer.” Let’s explore a couple of techniques that allow us to clear our answer of negative exponents.

Example $\PageIndex{10}$

Consider the expression: $\dfrac{x^2}{y^{-3}} \nonumber$

Simplify so that the resulting equivalent expression contains no negative exponents.

Solution

Raising y to the $−3$ means we have to cube and invert, so $y^{−3} = 1/y^3$ .

$\dfrac{x^2}{y^{-3}} = \dfrac{x^2}{\tfrac{1}{y^3}} \nonumber$

To divide $x^2$ by $1/y^3$ , we invert and multiply.

$\begin{align*} &= x^2 \div \dfrac{1}{y^{3}}\\ &= \dfrac{x^2}{1}\cdot \dfrac{y^{3}}{1}\\ &= x^2y^3 \end{align*} \nonumber$

Alternate approach: An alternate approach takes advantage of the laws of exponents. We begin by multiplying numerator and denominator by $y^3$ .

$\begin{align*} \dfrac{x^2}{y^{-3}} &= \dfrac{x^2}{y^{-3}} \cdot \dfrac{y^3}{y^{3}}\\ &= \dfrac{x^2y^3}{y^0}\\ &= x^2y^3 \end{align*} \nonumber$

In the last step, note how we used the fact that $y^0 = 1$

Exercise $\PageIndex{10}$

Simplify the expression $\dfrac{y^5}{x^{-2}} \nonumber$ so that the resulting equivalent expression contains no negative exponents.

Answer: $y^5x^2$

Example $\PageIndex{11}$

Consider the expression: $\dfrac{2x^2y^{-2}}{z^{3}} \nonumber$ Simplify so that the resulting equivalent expression contains no negative exponents.

Solution

Again, we can remove all the negative exponents by taking reciprocals. In this case $y^{−2} =1/y^2$ (square and invert).

$\begin{align*} \dfrac{2x^2y^{-2}}{z^{3}} &= \dfrac{2x^2\cdot \tfrac{1}{y ^2}}{z^{3}} \\ &= \dfrac{\tfrac{2x^2}{y^2}}{z^3} \end{align*} \nonumber$

To divide $2x^2/y^2$ by $z^3$ , we invert and multiply.

$\begin{align*} &= \dfrac{2x^2}{y^2}\div {z^{3}} \\ &= \dfrac{2x^2}{y^2}\cdot \dfrac{1}{z^3}\\ &= \dfrac{2x^2}{y^2z^3} \end{align*} \nonumber$

Alternate approach: An alternate approach again takes advantage of the laws of exponents. We begin by multiplying numerator and denominator by $y^2$ .

$\begin{align*} \dfrac{2x^2y^{-2}}{z^{3}} &= \dfrac{2x^2y^{-2}}{z^3}\cdot \dfrac{y^2}{y^2} \\ &= \dfrac{2x^2y^0}{y^2z^3}\\ &= \dfrac{2x^2}{y^2z^3} \end{align*} \nonumber$

In the last step, note how we used the fact that $y^0 = 1$ .

Exercise $\PageIndex{11}$

Simplify the expression $\dfrac{x^{-3}y^2}{3z^{-4}} \nonumber$ so that the resulting equivalent expression contains no negative exponents.

Answer: $\dfrac{y^2z^4}{3x^3}$

Search

Text Color

Text Size

Margin Size

Font Type

Laws of Exponents

Raising to a Negative Integer

Applying the Laws of Exponents

Clearing Negative Exponents

Support Center

How can we help?