7.3: Simplifying Rational Expressions

Last updated
Save as PDF

Page ID: 19893

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Any time you divide a polynomial by a second polynomial, you form what is You will ﬁnd that material quite helpful for this section. known as a rational expression.

Note

Readers are strongly encouraged to review the material on fractions presented in Section 3 of Chapter 1.

Rational expression

The expression \[\dfrac{p(x)}{q(x)} \nonumber\] where $p(x)$ and $q(x)$ are polynomials, is called a rational expression.

For example, each of the following is a rational expression.

$\dfrac{x+2}{3x}$
$\dfrac{x+3}{x^2-2x-4}$
$\dfrac{2x}{3y^2}$

In example a), the rational expression is composed of a binomial over a monomial. Example b) is constructed by dividing a binomial by a trinomial. Example c) is composed of a monomial over a monomial, the type of rational expression that will gain the most attention in this section.

Multiplying and Dividing Rational Expressions

We will concentrate on rational expressions with monomial numerators and denominators. Recall that to form the product of two rational numbers, we simply multiply numerators and denominators. The same technique is used to multiply any two rational expressions.

Multiplying rational expressions

Given $a/b$ and $c/d$, their product is deﬁned as:\[\dfrac{a}{b}\cdot \dfrac{c}{d}=\dfrac{ac}{bd} \nonumber \]

Remember, you need only multiply numerators and denominators. For example:

$\dfrac{x}{3}\cdot \dfrac{2}{y} = \dfrac{2x}{3y}$
$\dfrac{2a}{3b^2}\cdot \dfrac{5a}{9b^3} = \dfrac{10a^2}{27b^5}$
$\dfrac{x}{2y}\cdot \left (-\dfrac{3x}{4y^2} \right ) = -\dfrac{3x^2}{8y^3}$

Of course, as the next example shows, sometimes you also need to reduce your answer to lowest terms.

Example $\PageIndex{1}$

Simplify: $\dfrac{2}{x}\cdot \dfrac{x^2}{4}$.

Solution

Multiply numerators and denominators.

\[\dfrac{2}{x}\cdot \dfrac{x^2}{4} = \dfrac{2x^5}{4x^3} \nonumber \]

Now, there several diﬀerent ways you can reduce this answer to lowest terms, two of which are shown below.

You can factor numerator and denominator, then cancel common factors. \[\begin{align*} \dfrac{2x^5}{4x^3}&= \dfrac{2\cdot x\cdot x\cdot x\cdot x\cdot x}{2\cdot 2\cdot x\cdot x\cdot x}\\ &= \dfrac{\not{2}\cdot \not {x}\cdot \not{x}\cdot \not{x}\cdot x\cdot x}{\not{2}\cdot 2\cdot \not{x}\cdot \not{x}\cdot \not{x}}\\ &= \dfrac{x^2}{2} \end{align*} \nonumber\]

Or you can write the answer as a product, repeat the base and subtract exponents.\[\begin{align*} \dfrac{2x^5}{4x^3}&= \dfrac{2}{4}\cdot \dfrac{x^5}{x^3} \\ &= \dfrac{1}{2}\cdot x^{5-3} \\ &= \dfrac{1}{2}x^2 \end{align*} \nonumber \]

As dividing by $2$ is the same as multiplying by $1/2$, these answers are equivalent. Also, note that the right-hand method is more eﬃcient

Exercise $\PageIndex{1}$

Simply: $\dfrac{9}{x^2}\cdot \dfrac{x}{6}$.

Answer: $\dfrac{3}{2x}$

Recall that when dividing fractions, we invert the second fraction and multiply.

Dividing rational expressions

Given a/b and c/d, their quotient is deﬁned as:\[\begin{align*} \dfrac{a}{b}\div \dfrac{c}{d} &= \dfrac{a}{b}\cdot \dfrac{d}{c}\\ &= \dfrac{ad}{bc} \end{align*}\nonumber\]

Example $\PageIndex{2}$

Simplify: $\dfrac{x^2}{y}\div \dfrac{x^4}{2y^2}$.

Solution

Invert, then multiply.

\[\begin{align*} \dfrac{x^2}{y}\div \dfrac{x^4}{2y^2} &= \dfrac{x^2}{y}\cdot \dfrac{2y^2}{x^4}\\ &= \dfrac{2x^2y^2}{x^4y} \end{align*} \nonumber \]

Now, there several diﬀerent ways you can reduce this answer to lowest terms, two of which are shown below.

You can factor numerator and denominator, then cancel common factors. \[\begin{align*} \dfrac{2x^2y^2}{x^4y}&= \dfrac{2\cdot x\cdot x\cdot y\cdot y}{x\cdot x\cdot x\cdot x\cdot y}\\ &= \dfrac{2\cdot \not{x}\cdot \not{x}\cdot \not{y}\cdot y}{\not{x}\cdot \not{x}\cdot x\cdot x\cdot \not{y}}\\ &= \dfrac{2y}{x^2} \end{align*} \nonumber\]

Or you can write the answer as a product, repeat the base and subtract exponents.\[\begin{align*} \dfrac{2x^2y^2}{x^4y}&= 2\cdot \dfrac{x^2}{x^4}\cdot \dfrac{y^2}{y^1}\\ &= 2x^{-2}y^1\\ &= \dfrac{2y}{x^2} \end{align*} \nonumber\]In the last step, $x^{−2}$ is the same as $1/x^2$, then we multiply numerators and denominators.

Note that the right-hand method is more eﬃcient.

Exercise $\PageIndex{2}$

Simplify: $\dfrac{3y}{x^3}\div \dfrac{y^2}{4x}$.

Answer: $\dfrac{12}{x^2y}$

Adding and Subtracting Rational Expressions

First, recall the rules for adding or subtracting fractions that have a “common” denominator.

Adding rational expressions

Given $a/c$ and $b/c$, their sum is deﬁned as:\[\dfrac{a}{c} + \dfrac{b}{c}=\dfrac{a+b}{c} \nonumber\]That is, add the numerators and place the result over the common denominator.

The following examples each share a common denominator. We add the numerators, then place the result over the common denominator.

\[\dfrac{5}{7}+\dfrac{1}{7}=\dfrac{6}{7},\quad \dfrac{2}{x}+\dfrac{3}{x}=\dfrac{5}{x}, \quad \text {and} \quad \dfrac{x}{y}+\dfrac{3y}{y}=\dfrac{x+3y}{y} \nonumber\]

Example $\PageIndex{3}$

Simplify: $\dfrac{3x}{xy}+\dfrac{2y}{xy} \nonumber$.

Solution

Add the numerators, placing the result over the common denominator.

\[\dfrac{3x}{xy}+\dfrac{2y}{xy} = \dfrac{3x+2y}{xy} \nonumber\]

Exercise $\PageIndex{3}$

Simplify: $\dfrac{4x}{x^2y}+\dfrac{5y^2}{x^2y}$

Answer: $\dfrac{4x+5y^2}{x^2y}$

Subtracting rational expressions

Given $a/c$ and $b/c$, their diﬀerence is deﬁned as:\[\dfrac{a}{c} - \dfrac{b}{c}=\dfrac{a-b}{c} \nonumber\]That is, subtract the numerators and place the result over the common denominator.

The following examples each share a common denominator. We subtract the numerators, then place the result over the common denominator.

\[\dfrac{7}{9}-\dfrac{2}{9}=\dfrac{2}{9},\quad \dfrac{5a}{b}-\dfrac{3a}{b}=\dfrac{2a}{b}, \quad \text {and} \quad \dfrac{3x}{xy}-\dfrac{5y}{xy}=\dfrac{3x-5y}{xy} \nonumber\]

As the next example shows, sometimes you may have to reduce your answer to lowest terms.

Example $\PageIndex{4}$

Simplify: $\dfrac{5xy}{2z}-\dfrac{3xy}{2z}$.

Solution

Subtract the numerators, placing the result over the common denominator.

\[\begin{align*} \dfrac{5xy}{2z}-\dfrac{3xy}{2z} &= \dfrac{5xy-3xy}{2z}\\ &= \dfrac{2xy}{2z} \end{align*} \nonumber \]

To reduce to lowest terms, divide both numerator and denominator by $2$.

\[\dfrac{xy}{z} \nonumber \]

Exercise $\PageIndex{4}$

Simplify: $\dfrac{8x}{3yz^2}-\dfrac{2x}{3yz^2}$.

Answer: $\dfrac{2x}{yz^2}$

The Least Common Denominator

When adding or subtracting, if the rational expressions do not share a common denominator, you must ﬁrst make equivalent fractions with a common denominator.

Least common denominator

If the fractions $a/b$ and $c/d$ do not share a common denominator, then the least common denominator for $b$ and $d$ is deﬁned as the smallest number (or expression) divisible by both $b$ and $d$. In symbols, $\mathrm{LCD}(b,d)$ represents the least common denominator of $b$ and $d$.

Example $\PageIndex{5}$

Simplify: $\dfrac{x}{6}+\dfrac{2x}{9}$.

Solution

The smallest number divisible by both $6$ and $9$ is $18$; i.e., $\mathrm{LCD}(6,9) = 18$. We must ﬁrst make equivalent fractions with a common denominator of $18$.

\[\begin{align*} \dfrac{x}{6}+\dfrac{2x}{9} &= \dfrac{x}{6}\cdot {\color {Red}\dfrac{3}{3}}+\dfrac{2x}{9}\cdot {\color {Red}\dfrac{2}{2}}\\ &= \dfrac{3x}{18}+\dfrac{4x}{18} \end{align*} \nonumber \]

\[=\dfrac{7x}{18} \nonumber \]

Exercise $\PageIndex{5}$

Simplify: $\dfrac{3x}{8}+\dfrac{5x}{6}$.

Answer: $\dfrac{29x}{24}$

Example $\PageIndex{6}$

Simplify: $\dfrac{y}{8x}-\dfrac{y}{12x}$.

Solution

The smallest expression divisible by both $8x$ and $12x$ is $24x$; i.e., $\mathrm{LCD}(8x,12x) = 24x$. We must ﬁrst make equivalent fractions with a common denominator of $24x$, then place the diﬀerence of the numerators over the common denominator.

\[\begin{align*} \dfrac{y}{8x}-\dfrac{y}{12x} &= \dfrac{y}{8x}\cdot {\color {Red}\dfrac{3}{3}}-\dfrac{y}{12x}\cdot {\color {Red}\dfrac{2}{2}}\\ &= \dfrac{3y}{24x}-\dfrac{2y}{24x}\\ &= \dfrac{y}{24x} \end{align*} \nonumber\]

Exercise $\PageIndex{6}$

Simplify: $\dfrac{x}{8y}-\dfrac{x}{10y}$.

Answer: $\dfrac{x}{40y}$

In Example $\PageIndex{5}$, it was not diﬃcult to imagine the smallest number divisible by both $6$ and $9$. A similar statement might apply to Example $\PageIndex{6}$. This is not the case in all situations.

Example $\PageIndex{7}$

Simplify: $\dfrac{5y}{72}-\dfrac{y}{108}$.

Solution

In this example, it is not easy to conjure up the smallest number divisible by both $72$ and $108$. As we shall see, prime factorization will come to the rescue.

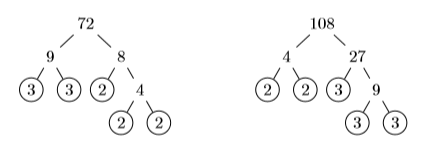
$fig 7.3.a.png$

Thus, $72 = 2^3\cdot 3^2$ and $108 = 2^2\cdot 3^3$.

Note: Procedure for ﬁnding the least common denominator (LCD)

To ﬁnd the least common denominator for two or more fractions, proceed as follows:

Prime factor each denominator, putting your answers in exponential form.
To determine the $\mathrm{LCD}$, write down each factor that appears in your prime factorizations to the highest power that it appears.

Following the procedure above, we list the prime factorization of each denominator in exponential form. The highest power of $2$ that appears is $2^3$. The highest power of $3$ that appears is $3^3$.

\[\begin{align*} 72 &= 2^3\cdot 3^2 \quad \color {Red} \text {Prime factor } 72.\\ 108 &= 2^2\cdot 3^3 \quad \color {Red} \text {Prime factor } 108.\\ \mathrm{LCD} &= 2^3\cdot 3^3 \quad \color {Red} \text {Highest power of } 2 \text { is } 2^3. \text { Highest power of } 3 \text { is } 3^3. \end{align*} \nonumber\]

Therefore, the $\mathrm{LCD}$ is $2^3\cdot 3^3 = 8\cdot 27$ or $216$. Hence:

\[\begin{align*} \dfrac{5y}{72}-\dfrac{y}{108} &= \dfrac{5y}{72}\cdot {\color {Red}\dfrac{3}{3}}-\dfrac{y}{108}\cdot {\color {Red}\dfrac{2}{2}} \quad \color {Red} \text {Make equivalent fractions.} \\ &= \dfrac{15y}{216}-\dfrac{2y}{216} \quad \color {Red} \text {Simplify.} \\ &= \dfrac{13y}{216} \quad \color {Red} \text {Subtract numerators.} \end{align*} \nonumber\]

Exercise $\PageIndex{7}$

Simplify: $\dfrac{7x}{36}-\dfrac{3x}{40}$.

Answer: $\dfrac{43x}{360}$

Example $\PageIndex{8}$

Simplify: $\dfrac{7}{15xy^2}-\dfrac{11}{20x^2}$

Solution

Prime factor each denominator, placing the results in exponential form.

\[\begin{align*} 15xy^2 &= 3\cdot 5\cdot x\cdot y^2 \\ 20x^2 &= 2^2 \cdot 5\cdot x^2 \end{align*} \nonumber \]

To ﬁnd the $\mathrm{LCD} $, list each factor that appears to the highest power that it appears.

\[\mathrm{LCD} = 2^2\cdot 3\cdot 5\cdot x^2 \cdot y^2 \nonumber \]

Simplify.

\[\mathrm{LCD} = 60 x^2 y^2 \nonumber \]

After making equivalent fractions, place the diﬀerence of the numerators over this common denominator.

\[\begin{align*} \dfrac{7}{15xy^2}-\dfrac{11}{20x^2} &= \dfrac{7}{15xy^2}\cdot {\color {Red}\dfrac{4x}{4x}}-\dfrac{11}{20x^2}\cdot {\color {Red}\dfrac{3y^2}{3y^2}}\\ &= \dfrac{28x}{60x^2y^2}-\dfrac{33y^2}{60x^2y^2}\\ &= \dfrac{28x-33y^2}{60x^2y^2} \end{align*} \nonumber \]

Exercise $\PageIndex{8}$

Simplify: $\dfrac{11}{18xy^2}+\dfrac{7x}{30xy}$

Answer: $\dfrac{55+21x^2}{90x^2y}$

Dividing a Polynomial by a Monomial

We know that multiplication is distributive with respect to addition; that is, $a(b + c)=ab + ac$. We use this property to perform multiplications such as: \[x^2(2x^2 −3x−8) = 2x^4 −3x^3 −8x^2 \nonumber \] However, it is also true that division is distributive with respect to addition.

Distributive property for division

If $a$, $b$, and $c$ are any numbers, then:\[\dfrac{a+b}{c} = \dfrac{a}{c}+\dfrac{b}{c} \nonumber \]

For example, note that\[\dfrac{4+6}{2} = \dfrac{4}{2}+\dfrac{6}{2} \nonumber \]

This form of the distributive property can be used to divide a polynomial by a monomial.

Example $\PageIndex{9}$

Divide $x^2 −2x−3$ by $x^2$.

Solution

We use the distributive property, dividing each term by $x^2$.

\[\dfrac{x^2-2x-3}{x^2} = \dfrac{x^2}{x^2}-\dfrac{2x}{x^2}-\dfrac{3}{x^2} \nonumber \]

Now we reduce each term of the last result to lowest terms, canceling common factors.

\[= 1-\dfrac{2}{x}-\dfrac{3}{x^2} \nonumber \]

Exercise $\PageIndex{9}$

Divide $9x^3+8x^2−6x$ by $3x^2$.

Answer: $3x+\dfrac{8}{3}-\dfrac{2}{x}$

Example $\PageIndex{10}$

Divide $2x^3 −3x + 12$ by $6x^3$.

Solution

We use the distributive property, dividing each term by $6x^3$.

\[\dfrac{2x^3-3x+12}{6x^3} = \dfrac{2x^3}{6x^3}-\dfrac{3x}{6x^3}+\dfrac{12}{6x^3} \nonumber\]

Now we reduce each term of the last result to lowest terms, canceling common factors.

\[= \dfrac{1}{3}-\dfrac{1}{2x^2}+\dfrac{2}{x^3} \nonumber\]

Exercise $\PageIndex{10}$

Divide $−4x^2 +6x−9$ by $2x^4$.

Answer: $-\dfrac{2}{x^2}+\dfrac{3}{x^3}-\dfrac{9}{x^4}$

Search

Text Color

Text Size

Margin Size

Font Type