7.2: Scientiﬁc Notation

Last updated

Feb 21, 2022
Save as PDF
- 7.1: Negative Exponents
- 7.3: Simplifying Rational Expressions

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

We begin this section by examining powers of ten.

$\begin{align*} 10^1 &= 10\\ 10^2 &= 10\cdot 10 = 100\\ 10^3 &= 10\cdot 10\cdot 10 = 1,000\\ 10^4 &= 10\cdot 10\cdot 10\cdot 10 = 10,000 \end{align*} \nonumber$

Note that the answer for $10^3$ is a one followed by three zeros. The answer for $10^4$ is a one followed by four zeros. Do you see the pattern?

Nonnegative powers of ten

In the expression $10^n$ , the exponent matches the number of zeros in the answer. Hence, $10^n$ will be a $1$ followed by $n$ zeros.

Example $\PageIndex{1}$

Simplify: $10^9$ .

Solution

$10^9$ should be a $1$ followed by $9$ zeros. $10^9 =1 ,000,000,000 \nonumber$

Exercise $\PageIndex{1}$

Simplify: $10^6$ .

Answer: $1,000,000$

Next, let’s examine negative powers of ten.

$\begin{align*} 10^{-1} &= \dfrac{1}{10} = 0.1\\ 10^{-2} &= \dfrac{1}{100} = 0.01\\ 10^{-3} &= \dfrac{1}{1000} = 0.001\\ 10^{-4} &= \dfrac{1}{10000} = 0.0001 \end{align*} \nonumber$

Note that the answer for $10^{−3}$ has three decimal places and the answer for $10^{−4}$ contains four decimal places.

Negative powers of ten

In the expression $10^{−n}$ , the exponent matches the number of decimal places in the answer. Hence, $10^{−n}$ will have n decimal places, the ﬁrst $n−1$ of which are zeros and the digit in the nth decimal place is a $1$ .

Example $\PageIndex{2}$

Simplify: $10^{−7}$ .

Solution

$10^{−7}$ should have seven decimal places, the ﬁrst six of which are zeros, and the digit in the seventh decimal place is a $1$ . $10^{−7} = 0 .0000001 \nonumber$

Exercise $\PageIndex{2}$

Simplify: $10^{−5}$ .

Answer: $0.00001$

Multiplying Decimal Numbers by Powers of Ten

Let’s multiply $1.234567$ by $10^3$ , or equivalently, by $1,000$ .

$\begin{array}{ccc} 1.234567 \\ \;\;\times 1000\\ \hline 1234.567000 \end{array} \nonumber$

The sum total of digits to the right of the decimal point in $1.234567$ and $1000$ is $6$ . Therefore, we place the decimal point in the product so that there are six digits to the right of the decimal point.

However, the trailing zeros may be removed without changing the value of the product. That is, $1.234567$ times $1000$ is $1234.567$ . Note that the decimal point in the product is three places further to the right than in the original factor. This observation leads to the following result.

Multiplying by a nonnegative power of ten

Multiplying a decimal number by $10^n$ , where $n = 0, 1, 2, 3, \ldots ,$ will move the decimal point $n$ places to the right.

Example $\PageIndex{3}$

Simplify: $325.6783×10^2$ .

Solution

Multiplying by $10^2$ will move the decimal point two places to the right. Thus: $325.6783×10^2 = 32,567.83 \nonumber$

Exercise $\PageIndex{3}$

Simplify: $23.57889×10^3$

Answer: $23,578.89$

Example $\PageIndex{4}$

Simplify: $1.25×10^5$ .

Solution

Multiplying by $10^5$ will move the decimal point two places to the right. In this case, we need to add zeros at the end of the number to accomplish moving the decimal $5$ places to the right. $1.25×105 = 125,000 \nonumber$

Exercise $\PageIndex{14}$

Simplify: $2.35×10^4$

Answer: $23,500$

Let’s multiply $453.9$ by $10^{−2}$ , or equivalently, by $0.01$ .

$\begin{array}{ccc} 453.9 \\ \times 0.01\\ \hline 4.539 \end{array} \nonumber$

The sum total of digits to the right of the decimal point in $453.9$ and $0.01$ is $3$ . Therefore, we place the decimal point in the product so that there are $3$ digits to the right of the decimal point. That is, $453.9×10^{−2} = 4.539$ . Note that the decimal point in the product is two places further to the left than in the original factor. This observation leads to the following result.

Multiplying by a negative power of ten

Multiplying a decimal number by $10^{−n}$ , where $n = 1, 2, 3, \ldots ,$ will move the decimal point $n$ places to the left.

Example $\PageIndex{5}$

Simplify: $14,567.8×10^{−3}$ .

Solution

Multiplying by $10^{−3}$ will move the decimal point three places to the left. Thus: $14,567.8×10^{−3} = 14 .5678 \nonumber$

Exercise $\PageIndex{5}$

Simplify: $3,854.2×10^{−1}$

Answer: $385 .42$

Example $\PageIndex{6}$

Simplify: $4.3×10^{−4}$ .

Solution

Multiplying by $10^{−4}$ will move the decimal point four places to the left. In this case, we need to add some leading zeros at the beginning of the number to accomplish moving the decimal $4$ places to the left. $4.3×10^{−4} =0.00043\nonumber$ . Note also the leading zero before the decimal point. Although $.00043$ is an equivalent number, the form $0.00043$ is preferred in mathematics and science.

Exercise $\PageIndex{6}$

Simplify: $2.2×10^{−2}$

Answer: $0.022$

Scientiﬁc Notation Form

We start by deﬁning the form of a number called scientiﬁc notation.

Scientiﬁc notation

A number having the form $a×10^b \nonumber$ where $b$ is an integer and $1 ≤| a| < 10$ , is said to be in scientiﬁc notation.

The requirement $1 ≤| a| < 10$ says that the magnitude of a must be a least $1$ and less than $10$ .

The number $12.34×10^{−4}$ is not in scientiﬁc notation because $|12.34| = 12.34$ is larger than $10$ .
The number $−0.95×10^3$ is not in scientiﬁc notation because $|−0.95|= 0.95$ is less than $1$ .
The number $7.58×10^{−12}$ is in scientiﬁc notation because $|7.58|=7.58$ is greater than or equal to $1$ and less than $10$ .
The number $−1.0×10^{15}$ is in scientiﬁc notation because $|−1.0|=1.0$ is greater than or equal to $1$ and less than $10$ .

After contemplating these examples, it follows that a number in scientiﬁc notation should have exactly one of the digits $1, 2, 3, \ldots , 9$ before the decimal point. Exactly one, no more, no less. Thus, each of the following numbers is in scientiﬁc notation.

$4.7×10^8, \quad −3.764×10^{−1}, \quad 3.2×10^0, \quad \text {and} \quad −1.25×10^{−22} \nonumber$

Placing a Number in Scientiﬁc Notation

To place a number into scientiﬁc notation, we need to move the decimal point so that exactly one of the digits $1, 2, 3, \ldots , 9$ remains to the left of the decimal point, then multiply by the appropriate power of $10$ so that the result is equivalent to the original number.

Example $\PageIndex{7}$

Place the number $1,234$ in scientiﬁc notation.

Solution

Move the decimal point three places to the left so that it is positioned just after the $1$ . To make this new number equal to $1,234$ , multiply by $10^3$ . Thus: $1,234 = 1.234×10^3 \nonumber$

Check: Multiplying by $10^3$ moves the decimal three places to the right, so: $1.234×10^3 =1,234 \nonumber$ This is the original number, so our scientiﬁc notation form is correct.

Exercise $\PageIndex{7}$

Place the number $54,321$ in scientiﬁc notation.

Answer: $5 .4321×10^4$

Example $\PageIndex{8}$

Place the number $0.000025$ in scientiﬁc notation.

Solution

Move the decimal point ﬁve places to the right so that it is positioned just after the $2$ . To make this new number equal to $0.000025$ , multiply by $10^{−5}$ . Thus: $0.000025 = 2.5×10^{−5} \nonumber$

Check: Multiplying by $10^{−5}$ moves the decimal ﬁve places to the left, so: $2.5×10^{−5} = 0 .000025 \nonumber$ This is the original number, so our scientiﬁc notation form is correct.

Exercise $\PageIndex{8}$

Place the number $0.0175$ in scientiﬁc notation.

Answer: $1.75×10^{−2}$

Example $\PageIndex{9}$

Place the number $34.5×10^{−11}$ in scientiﬁc notation.

Solution

First, move the decimal point one place to the left so that it is positioned just after the three. To make this new form equal to $34.5$ , multiply by $10^1$ . $34.5×10^{−11} = 3.45×10^1×10^{−11} \nonumber$ Now, repeat the base $10$ and add the exponents.

$=3 .45×10^{−10} \nonumber$

Exercise $\PageIndex{9}$

Place the number $756.98×10^{−5}$ in scientiﬁc notation.

Answer: $7.5698×10^{−3}$

Example $\PageIndex{10}$

Place the number $0.00093×10^{12}$ in scientiﬁc notation.

Solution

First, move the decimal point four places to the right so that it is positioned just after the nine. To make this new form equal to $0.00093$ , multiply by $10^{−4}$ . $0.00093×10^{12} = 9.3×10^{−4} ×10^{12} \nonumber$

Now, repeat the base $10$ and add the exponents. $=9.3×10^8 \nonumber$

Exercise $\PageIndex{10}$

Place the number $0.00824×10^8$ in scientiﬁc notation.

Answer: $8.24×10^5$

Scientiﬁc Notation and the Graphing Calculator

The TI-84 graphing calculator has a special button for entering numbers in scientiﬁc notation. Locate the “comma” key just about the number $7$ key on the calculator’s keyboard (see Figure $\PageIndex{1}$ ). Just above the “comma” key, printed on the calculator’s case is the symbol EE. It’s in the same color as the 2^nd key, so you’ll have to use the 2^nd key to access this symbol.

fig 7.2.1.png — Figure $\PageIndex{1}$ : Locate the EE label above the “comma” key on the keyboard.

We know that $2.3 × 10^2 = 230$ . Let’s see if the calculator gives the same interpretation.

Enter $2.3$ .
Press the 2^nd key, then the comma key. This will put E on the calculator view screen.
Enter a $2$ .
Press ENTER.

fig 7.2.2.png — Figure $\PageIndex{2}$ : Entering numbers in scientiﬁc notation.

The result of these steps is shown in the ﬁrst image in Figure $\PageIndex{2}$ . Note that the calculator interprets $2.3\mathbf{E}2$ as $2.3×10^2$ and gives the correct answer, $230$ . You can continue entering numbers in scientiﬁc notation (see the middle image in Figure $\PageIndex{2}$ ). However, at some point the numbers become too large and the calculator responds by outputting the numbers in scientiﬁc notaiton. You can also force your calculator to display numbers in scientiﬁc notation in all situations, by ﬁrst pressing the MODE key, then selecting SCI on the ﬁrst line and pressing the ENTER key (see the third image in Figure $\PageIndex{2}$ ). You can return your calculator to “normal” mode by selecting NORMAL and pressing the ENTER key.

Example $\PageIndex{11}$

Use the graphing calculator to simplify: $(2.35×10^{−12})(3.25×10^{−4}) \nonumber$

Solution

First, note that we can approximate $(2.35×10^{−12})(3.25×10^{−4})$ by taking the product of $2$ and $3$ and adding the powers of ten.

$\begin{align*} &(2.35\times 10^{-12})(3.25\times 10^{-4}) \\ &\approx (2\times 10^{-12})(3\times 10^{-4}) \quad \color {Red} \text {Approximate: } 2.35\approx 2 \text { and } 3.25\approx 3 \\ &\approx 6\times 10^{-16} \quad \color {Red} 2\cdot 3 = 6 \text { and } 10^{-12}\cdot 10^{-4} = 10^{-16} \end{align*} \nonumber$

The graphing calculator will provide an accurate answer. Enter $2.35\mathbf{E}-12$ , press the “times” button, then enter 3.25E-4 and press the ENTER button. Be sure to use the “negate” button and not the “subtract” button to produce the minus sign. The result is shown in Figure $\PageIndex{3}$ .

fig 7.2.3.png — Figure $\PageIndex{3}$ : Computing $(2.35×10^{−12})(3.25×10^{−4})$ .

Thus, $(2.35×10^{−12})(3.25×10^{−4})=7 .6375×10^{−16}$ . Note that this is fairly close to our estimate of $6 ×10^{−16}$ .

Exercise $\PageIndex{11}$

Use the graphing calculator to simplify: $(3.42×10^6)(5.86×10^{−9}) \nonumber$

Answer: $2.00412×10^{−2}$

Reporting your answer on your homework

After computing the answer to Example $\PageIndex{11}$ on your calculator, write the following on your homework: $(2.35×10^{−12})(3.25×10^{−4})=7.6375×10^{−16} \nonumber$ Do not write $7.6375\mathbf{E}-16$ .

Example $\PageIndex{12}$

Use the graphing calculator to simplify: $\dfrac{6.1\times 10^{-3}}{(2.7\times 10^4)(1.1\times 10^8)} \nonumber$

Solution

Again, it is not diﬃcult to produce an approximate answer.

$\begin{align*} &\dfrac{6.1\times 10^{-3}}{(2.7\times 10^4)(1.1\times 10^8)} \\ &\approx \dfrac{6\times 10^{-3}}{(3\times 10^4)(1\times 10^8)} \quad \color {Red} 6.1\approx 6, 2.7\approx 3, \text { and } 1.1\approx 1 \\ &\approx \dfrac{6\times 10^{-3}}{3\times 10^{12}} \quad \color {Red} 3\cdot 1=3 \text { and } 10^{4}\cdot 10^{8} = 10^{12}\\ &\approx \dfrac{6}{3}\cdot \dfrac{10^{-3}}{10^{12}} \quad \color {Red} \dfrac{ac}{bd}=\dfrac{a}{b}\cdot \dfrac{c}{d}\\ &\approx 2\times 10^{-15} \quad \color {Red} \dfrac{6}{3}=2 \text { and } \dfrac{10^{-3}}{10^{12}}=10^{-15} \end{align*} \nonumber$

Let’s get a precise answer with our calculator. Enter the numerator as $6.1\mathbf{E}3$ , then press the “division” button. Remember that we must surround the denominator with parentheses. So press the open parentheses key, then enter $2.7\mathbf{E}4$ . Press the “times” key, then enter $1.1\mathbf{E}8$ . Press the close parentheses key and press the ENTER button. The result is shown in Figure $\PageIndex{4}$ .

fig 7.2.4.png — Figure $\PageIndex{4}$ : Computing $6.1×10^{−3}/(2.7×10^4 ×1.1×10^8)$ .

Thus, $6.1×10^{−3}/(2.7×10^4 ×1.1×10^8)=2 .05387205×10^{−15}$ . Note that this is fairly close to our estimate of $2×10^{−15}$ .

Exercise $\PageIndex{12}$

Use the graphing calculator to simplify: $\dfrac{2.6\times 10^{4}}{(7.1\times 10^{-2})(6.3\times 10^7)} \nonumber$

Answer: $5.8126537×10^{−3}$

Example $\PageIndex{13}$

Isaac Newton’s universal law of gravitation is deﬁned by the formula $F = \dfrac{GmM}{r^2} \nonumber$ where $F$ is the force of attraction between two objects having mass $m$ and $M$ , $r$ is the distance between the two objects, and $G$ is Newton’s gravitational constant deﬁned by: $G =6 .67428\times 10^{-11} \text {N(m/kg)}^2 \nonumber$ Given that the mass of the moon is $7.3477×10^{22}$ kilograms (kg), the mass of the earth is $5.9736×10^{24}$ kilograms (kg), and the average distance between the moon and the earth is $3.84403×10^8$ meters (m), ﬁnd the force of attraction between the earth and the moon (in newtons (N)).

Solution

Plug the given numbers into Newton’s universal law of gravitation.

$F=\dfrac{GmM}{r^2} \nonumber$

$F=\dfrac{(6.673\times 10^{-11})(7.3477\times 10^{22})(5.9736\times 10^{24})}{(3.84403\times 10^8)^2} \nonumber$

Enter the expression into your calculator (see Figure $\PageIndex{5}$ ) as:

$(6.673\mathbf{E}-11*7.3477\mathbf{E}22*5.9736\mathbf{E}24)/(3.84403\mathbf{E}8)\wedge 2 \nonumber$

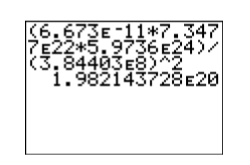
fig 7.2.5.png — Figure $\PageIndex{5}$ : Computing force of attraction between earth and the moon.

Hence, the force of attraction between the earth and the moon is approximately $1.98×10^{20}$ newtons (N).

Exercise $\PageIndex{13}$

The mass of the International Space Station is $450,000$ kg, and its average distance to the center of the earth is $387,000$ m. Find the force of attraction between the earth and the station (in newtons (N)).

Answer: $≈ 1.20×109 N$

Example $\PageIndex{14}$

The closest star to the earth is Alpha Centauri, $4.37$ light-years from the earth. A light-year is the distance that light will travel in one-year’s time. The speed of light is $186,000$ miles per second. How many miles from the earth is Alpha Centauri?

Solution

Because the speed of light is measured in miles per second, let’s ﬁrst compute the number of seconds in $4.37$ years. Because there are $365$ days in a year, $24$ hours in a day, $60$ minutes in an hour, and $60$ seconds in a minute, we can write:

$\begin{aligned} 4.37 \text {yr} &= 4.37\text {yr}\times 365\dfrac{\text {day}}{\text {yr}}\times 24\dfrac{\text {hr}}{\text {day}}\times 60\dfrac{\text {min}}{\text {hr}}\times 60\dfrac{\text {s}}{\text {min}}\\ &= 4.37{\color {Red}\not {\color {Black}\text {yr}}}\times 365\dfrac{\color {Red}\not {\color {Black}\text {day}}}{\color {Red}\not {\color {Black}\text {yr}}}\times 24\dfrac{\color {Red}\not {\color {Black}\text {hr}}}{\color {Red} \not {\color {Black}\text {day}}}\times 60\dfrac{\color {Red}\not {\color {Black}\text {min}}}{\color {Red}\not {\color {Black}\text {hr}}}\times 60\dfrac{\text {s}}{\color {Red}\not {\color {Black}\text {min}}} \end {aligned} \nonumber$

Note how the units cancel, indicating that the ﬁnal answer is in seconds. With our calculator mode set to scientiﬁc notation (see the image on the right in Figure $\PageIndex{2}$ ), we multiply the numbers to get the result shown in Figure $\PageIndex{6}$ . Rounding, the number of seconds in $4.37$ years is approximately $1.38 × 10^8$ seconds.

Next, we compute the distance the light travels in $4.37$ years. Using the fact that the distance traveled equals the speed times the time traveled, we have:

$\begin{aligned} \text {Distance} &= \text {Speed}\times \text {Time}\\ &= 1.86\times 10^5\dfrac{\text {mi}}{\text {s}}\cdot 1.38\times 10^8\text {s}\\ &= 1.86\times 10^5\dfrac{\text {mi}}{\color {Red}\not {\color {Black}\text {s}}}\cdot 1.38\times 10^8 {\color {Red}\not {\color {Black}\text {s}}} \end {aligned} \nonumber$

Note how the units cancel, indicating that our answer is in miles. Again, with our calculator set in scientiﬁc notation mode, we compute the product of $1.86×10^5$ and $1.38×10^8$ . The result is shown in the image on the right in Figure $\PageIndex{6}$ .

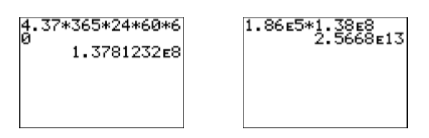
fig 7.2.6.png — Figure $\PageIndex{6}$ : Computing the distance to Alpha Centauri in miles.

Thus, the star Alpha Centauri is approximately $2.5668×10^{13}$ miles from the earth, or $2.5668×10^{13} \text {miles} ≈ 25,668,000,000,000 \text {miles} \nonumber$ pronounced “twenty-ﬁve quadrillion, six hundred sixty-eight trillion miles.”

Exercise $\PageIndex{14}$

The star Sirius is $8.58$ light-years from the earth. How many miles from the earth is Sirius?

Answer: $≈ 5.2425×10^{13}$ miles

Search

Text Color

Text Size

Margin Size

Font Type

Multiplying Decimal Numbers by Powers of Ten

Scientiﬁc Notation Form

Placing a Number in Scientiﬁc Notation

Scientiﬁc Notation and the Graphing Calculator

Support Center

How can we help?