7.4: Solving Rational Equations

Last updated
Save as PDF

Page ID: 19894

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

In Section 3 of Chapter 2, we showed that the most eﬃcient way to solve an equation containing fractions was to ﬁrst clear the fractions by multiplying both sides of the equation by the least common denominator. For example, given the equation

\[\dfrac{1}{2}x+\dfrac{1}{3}=\dfrac{1}{4} \nonumber \]

we would ﬁrst clear the fractions by multiplying both sides by $12$.

\[\begin{align*} 12\left [ \dfrac{1}{2}x + \dfrac{1}{3}\right ] &= \left [ \dfrac{1}{4} \right ]12\\ 6x+4 &= 3 \end{align*} \nonumber \]

This procedure works equally well when the the denominators contain a variable.

Example $\PageIndex{1}$

Solve for $x$: $1-\dfrac{2}{x} = \dfrac{3}{x^2}$

Solution

The common denominator is $x^2$. We begin by clearing fractions, multiplying both sides of the equation by $x^2$.

\[\begin{align*} 1-\dfrac{2}{x} &= \dfrac{3}{x^2} \quad \color {Red} \text {Original equation.}\\ {\color {Red} x^2}\left [1- \dfrac{2}{x} \right] &= \left [ \dfrac{3}{x^2} \right ]{\color {Red} x^2} \quad \color {Red} \text {Multiply both sides by } x^2. \end{align*} \nonumber \]

Now we use the distributive property.

\[{\color {Red} x^2}[1]-{\color {Red} x^2}\left [\dfrac{2}{x} \right ] = \left [\dfrac{3}{x^2} \right ]{\color {Red} x^2} \quad \color {Red} \text {Distribute } x^2. \nonumber \]

Now we cancel common factors and simplify.

\[x^2 - 2x =3 \quad \color {Red} \text {Cancel. Simplify. } \nonumber \]

The resulting equation is nonlinear ($x$ is raised to a power larger than $1$). Make one side zero, then factor.

\[\begin{align*} x^2-2x-3 &= 0 \quad \color {Red} \text {Nonlinear. Make one side zero.}\\ (x-3)(x+1) &= 0 \quad \color {Red} \text {Factor.} \end{align*} \nonumber \]

Use the zero product property to complete the solution. Either the ﬁrst factor is zero or the second factor is zero.

\[\begin{align*} x-3 &= 0 \\ x &= 3 \end{align*} \nonumber\]

\[\begin{align*} x+1 &= 0 \\ x &= -1 \end{align*} \nonumber\]

Hence, the solutions are $x = −1$ and $x = 3$.

Check. Substitute $−1$ for $x$, then $3$ for $x$ in the original equation and simplify.

\[\begin{align*} 1-\dfrac{2}{x} &= \dfrac{3}{x^2} \\ 1-\dfrac{2}{({\color {Red} -1})^2} &= \dfrac{3}{({\color {Red} -1})^2} \\ 1+2 &= 3\\ 3 &= 3 \end{align*} \nonumber\]

and

\[\begin{align*} 1-\dfrac{2}{x} &= \dfrac{3}{x^2} \\ 1-\dfrac{2}{({\color {Red} 3})} &= \dfrac{3}{({\color {Red} 3})^2} \\ 1-\dfrac{2}{3} &= \dfrac{3}{9}\\ \dfrac{1}{3} &= \dfrac{1}{3} \end{align*} \nonumber\]

Note that both result in true statements, showing that both $x =−1$ and $x =3$ check in the original equation.

Exercise $\PageIndex{1}$

Solve for $x$: $1-\dfrac{6}{x} = -\dfrac{8}{x^2}$

Answer: $2,4$

Example $\PageIndex{2}$

Solve for $x$: $6-\dfrac{22}{x^2}=\dfrac{29}{x}$

Solution

The common denominator is $x^2$.

\[\begin{align*} 6-\dfrac{22}{x^2} &= \dfrac{29}{x} \quad \color {Red} \text {Original equation.}\\ {\color {Red} x^2}\left [6-\dfrac{22}{x^2} \right ] &= \left [\dfrac{29}{x} \right ] {\color {Red} x^2} \quad \color {Red} \text {Multiply both sides by } x^2\\ {\color {Red} x^2}[6]-{\color {Red} x^2}\left [\dfrac{22}{x^2} \right ] &= \left [\dfrac{29}{x} \right ] {\color {Red} x^2} \quad \color {Red} \text {Distribute } x^2 \\ 6x^2-22 &= 29x \quad \color {Red} \text {Cancel and Simplify.} \end{align*} \nonumber \]

This last equation is nonlinear. Make one side zero.

\[6x^2 −29x−22 = 0 \nonumber \]

The integer pair $4$ and $−33$ has product $ac = −132$ and sum $b = −29$. Break up the middle term into a sum using this pair, then factor by grouping.

\[\begin{align*} 6x^2 +4x-33x-22 &= 0 \\ 2x(3x + 2)-11(3x + 2) &= 0 \\ (2x - 11)(3x + 2) &= 0 \end{align*} \nonumber \]

Finally, use the zero product property to write:

\[\begin{align*} 2x - 11 &= 0 \\ 2x &= 11 \\ x &= \dfrac{11}{2} \end{align*} \nonumber \]

\[\begin{align*} 3x + 2 &= 0 \\ 3x &= -2 \\ x &= -\dfrac{2}{3} \end{align*}\]

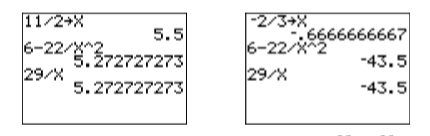
Check: Let’s check these solutions with our calculators. Enter $11/2$, push the STO► button, push the $\mathrm{X,T,\theta,n}$ button and the ENTER key (see the calculator screen on the left in Figure $\PageIndex{1}$). Next, enter the left-hand side of the equation as $6-22/X^2$ and press ENTER. Enter the right-hand side of the equation as $29/X$ and press ENTER. The results are the same (see the calculator screen on the left in Figure $\PageIndex{1}$ ). This veriﬁes that $11/2$ is a solution of $6−22/x^2 = 29/x$.

The calculator screen on the right in Figure $\PageIndex{1}$ shows a similar check of the solution $x = −2/3$.

fig 7.4.1.png — Figure $\PageIndex{1}$: Checking the solutions of $6-\dfrac{22}{x^2}=\dfrac{29}{x}$

Exercise $\PageIndex{2}$

Solve for $x$: $\dfrac{7}{x^2}+8=-\dfrac{30}{x}$

Answer: $−1/4, −7/2$

Solving Rational Equations with the Graphing Calculator

Let’s use the graphing calculator to solve an equation containing rational expressions.

Example $\PageIndex{3}$

Consider the following equation: \[2-\dfrac{9}{x}=\dfrac{5}{x^2} \nonumber \]Solve the equation algebraically, then solve the equation graphically using your graphing calculator. Compare your solutions.

Solution

Algebraic solution: First, an algebraic approach. Multiply both sides of the equation by the common denominator $x^2$.

\[\begin{align*} 2-\dfrac{9}{x} &= \dfrac{5}{x^2} \quad \color {Red} \text {Original equation.}\\ {\color {Red} x^2}\left [2-\dfrac{9}{x} \right ] &= \left [\dfrac{5}{x^2} \right ] {\color {Red} x^2} \quad \color {Red} \text {Multiply both sides by } x^2\\ {\color {Red} x^2}[2]-{\color {Red} x^2}\left [\dfrac{9}{x} \right ] &= \left [\dfrac{5}{x^2} \right ] {\color {Red} x^2} \quad \color {Red} \text {Distribute } x^2 \\ 2x^2-9x &= 5 \quad \color {Red} \text {Cancel and Simplify.} \end{align*} \nonumber\]

The last equation is nonlinear. Make one side zero.

\[2x^2 −9x−5=0 \quad \color {Red} \text {Make one side zero.} \nonumber \]

The integer pair $−10$ and $1$ have product equaling $ac = −10$ and sum equaling $b = −9$. Break up the middle term using this pair, then factor by grouping.

\[\begin{align*} 2x^2-10x+x-5 &= 0 \quad \color {Red} -10x+x=-9x\\ 2x(x-5) + 1(x-5) &= 0 \quad \color {Red} \text {Factor by grouping.} \\ (2x + 1)(x-5) &= 0 \quad \color {Red} \text {Factor out } x-5 \end{align*} \nonumber\]

Now use the zero product property to write:

\[\begin{align*} 2x+1 &= 0\\ 2x &= -1\\ x &= -\dfrac{1}{2} \end{align*} \nonumber \]

\[\begin{align*} x-5 &= 0\\ x &= 5 \end{align*} \nonumber\]

Hence, the solutions are $x = −1/2$ and $x = 5$.

Graphical solution: We could load each side of the equation separately, then use the intersect utility to ﬁnd where the graphs intersect. However, in this case, it’s a bit easier to make one side of the equation zero, draw a single graph, then note where the graph crosses the $x$-axis.

\[\begin{align*} 2-\dfrac{9}{x} &= \dfrac{5}{x^2} \quad \color {Red} \text {Original equation.} \\ 2-\dfrac{9}{x} - \dfrac{5}{x^2} &= 0 \quad \color {Red} \text {Make one side zero.} \nonumber \end{align*} \nonumber\]

Load the left-hand side of the equation into $\mathrm{Y1}$ as $\mathrm{2-9/X-5/X}\land 2$ (see the image on the left in Figure $\PageIndex{2}$), then select 6:ZStandard from the ZOOM menu to produce the image at the right in Figure $\PageIndex{2}$.

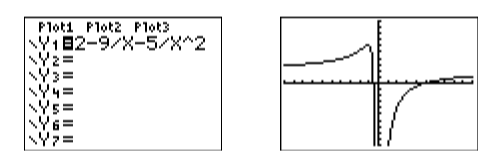
fig 7.4.2.png — Figure $\PageIndex{2}$: Sketch the graph of $y=2-\dfrac{9}{x}-\dfrac{5}{x^2}$.

Next, the solutions of

\[2-\dfrac{9}{x}-\dfrac{5}{x^2} = 0 \nonumber \]

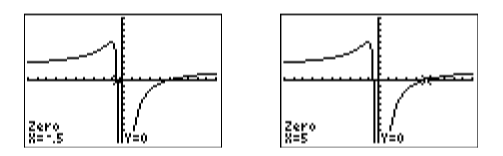
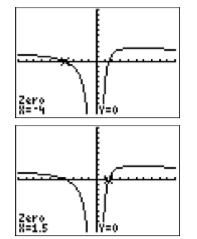
are found by noting where the graph of $y=2-\dfrac{9}{x}-\dfrac{5}{x^2}$ cross the $x$-axis. Select 2:zero from the CALC menu. Use the arrow keys to move the cursor to the left of the ﬁrst $x$-intercept, then press ENTER to set the “Left bound.” Next, move the cursor to the right of the ﬁrst $x$-intercept, then press ENTER to set the “Right bound.” Finally, leave the cursor where it is and press ENTER to set your “Guess.” The calculator responds with the result shown in the ﬁgure on the left in Figure $\PageIndex{3}$.

Repeat the zero-ﬁnding procedure to capture the coordinates of the second $x$-intercept (see the image on the right in Figure $\PageIndex{3}$).

fig 7.4.3.png — Figure $\PageIndex{3}$: Locating the zeros of $y=2-\dfrac{9}{x}-\dfrac{5}{x^2}$.

Reporting the solution on your homework: Duplicate the image in your calculator’s viewing window on your homework page. Use a ruler to draw all lines, but freehand any curves.

Label the horizontal and vertical axes with $x$ and $y$, respectively (see Figure $\PageIndex{4}$).
Place your WINDOW parameters at the end of each axis (see Figure $\PageIndex{4}$).
Label the graph with its equation (see Figure $\PageIndex{4}$).
Drop dashed vertical lines through each $x$-intercept. Shade and label the $x$-values of the points where the dashed vertical line crosses the $x$-axis. These are the solutions of the equation $2− 9/x− 5/x^2 = 0$ (see Figure $\PageIndex{4}$).

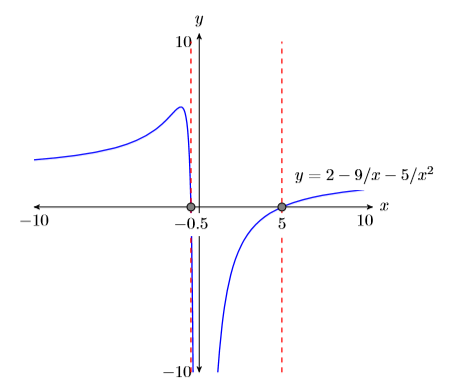
fig 7.4.4.png — Figure $\PageIndex{4}$: Reporting your graphical solution on your homework.

Thus, the calculator is reporting that the solutions of $2−9/x −5/x^2 = 0$ are $x =−0.5$ and $x = 5$, which match the algebraic solutions $x = −1/2$ and $x = 5$.

Exercise $\PageIndex{3}$

Solve the equation $2+\dfrac{5}{x}=\dfrac{12}{x^2}$ both algebraically and graphically, then compare your solutions.

Answer

$−4, 3/2$

$Ex 7.4.3.png$

Numerical Applications

Let’s apply what we’ve learned to an application.

Example $\PageIndex{4}$

The sum of a number and its reciprocal is $41/20$. Find the number.

Solution

In the solution, we address each step of the Requirements for Word Problem Solutions.

Set up a variable dictionary: Let $x$ represent the unknown number.
Set up an equation: If the unknown number is $x$, then its reciprocal is $1/x$. Thus, the “sum of a number and its reciprocal is $41/20$” becomes:\[x+\dfrac{1}{x}=\dfrac{41}{20} \nonumber \]
Solve the equation: Clear the fractions by multiplying both sides by $20x$, the least common denominator.\[\begin{align*} x+\dfrac{1}{x} &= \dfrac{41}{20} \quad \color {Red} \text {Model equation.}\\ {\color {Red}20x}\left [x+\dfrac{1}{x} \right ] &= \left [\dfrac{41}{20} \right ]{\color {Red}20x} \quad \color {Red} \text {Multiply both sides by }20x\\ {\color {Red}20x}[x]+{\color {Red}20x}\left [\dfrac{1}{x} \right ] &= \left [\dfrac{41}{20} \right ]{\color {Red}20x} \quad \color {Red} \text {Distribute }20x.\\ 20x^2+20 &= 41x \quad \color {Red} \text {Cancel and simplify.} \end{align*} \nonumber \]The equation is nonlinear. Make one side zero.\[20x^2 −41x + 20 = 0 \quad \color {Red} \text {Make one side zero.}\nonumber \]The integer pair $−16$ and $−25$ has product $ac = 400$ and sum $b = −41$. Break up the middle term in the last equation into a sum of like terms using this pair, then factor by grouping.\[\begin{align*} 20x^2 - 16x-25x + 20 &= 0 \quad \color {Red} -16x-25x=-41x\\ 4x(5x-4)-5(5x-4) &= 0 \quad \color {Red} \text {Factor by grouping.}\\ (4x-5)(5x-4) &= 0 \quad \color {Red} \text {Factor out }5x-4.\\ \end{align*} \nonumber \]We can now use the zero product property to write: \[\begin{align*} 4x-5 &= 0 \\ 4x &= 5 \\ x &= \dfrac{5}{4} \end{align*} \nonumber\]or\[\begin{align*} 5x-4 &= 0 \\ 5x &= 4 \\ x &= \dfrac{4}{5} \end{align*} \nonumber\]
Answer the question: There are two possible numbers, $5/4$ and $4/5$.
Look back: The sum of the unknown number and its reciprocal is supposed to equal $41/20$. The answer $5/4$ has reciprocal $4/5$. Their sum is:\[\begin{align*} \dfrac{5}{4} + \dfrac{4}{5} &= \dfrac{16}{20} + \dfrac{25}{20}\\ &= \dfrac{41}{20} \end{align*} \nonumber\]Thus, $5/4$ is a valid solution. The second answer $4/5$ has reciprocal $5/4$, so it is clear that their sum is also $41/20$. Hence, $4/5$ is also a valid solution.

Exercise $\PageIndex{4}$

The sum of a number and its reciprocal is $53/14$. Find the number.

Answer: $2/7, 7/2$

Search

Text Color

Text Size

Margin Size

Font Type