7.10: Exercise Supplement
( \newcommand{\kernel}{\mathrm{null}\,}\)
Exercise Supplement
Graphing Linear Equations and Inequalities in One Variable
For the following problems, graph the equations and inequalities.
6x−18=6

- Answer
-
x=4
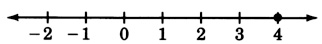
4x−3=−7

5x−1=2

- Answer
-
x=35
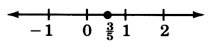
10x−16<4

−2y+1≤5

- Answer
-
y≥−2
−7a12≥2

3x+4≤12

- Answer
-
x≤83
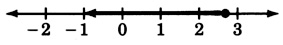
−16≤5x−1≤−11

0<−3y+9≤9

- Answer
-
0≤y<3
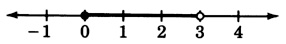
−5c2+1=7

Plotting Points in the Plane
Draw a coordinate system and plot the following ordered pairs.
(3,1),(4,−2),(−1,−3),(0,3),(3,0),(5,−23)
- Answer
-
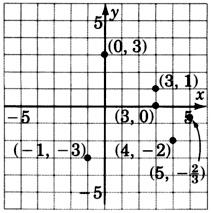
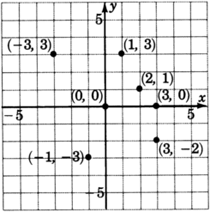
As accurately as possible, state the coordinates of the points that have been plotted on the graph.
Graphing Linear Equations in Two Variables
What is the geometric structure of the graph of all the solutions to the linear equation y=4x−9?
- Answer
-
a straight line
Graphing Linear Equations in Two Variables - Graphing Equations in Slope-Intercept Form
For the following problems, graph the equations.
y−x=2
y+x−3=0
- Answer
-
−2x+3y=−6
2y+x−8=0
- Answer
-
4(x−y)=12
3y−4x+12=0
- Answer
-
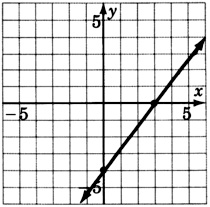
y=−3
y−2=0
- Answer
-
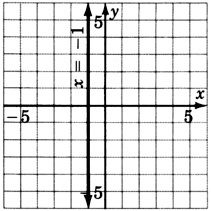
x=4
x+1=0
- Answer
-
x=0
y=0
- Answer
-
The Slope-Intercept Form of a Line
Write the slope-intercept form of a straight line.
The slope of a straight line is a ____ of the steepness of the line.
- Answer
-
measure
Write the formula for the slope of a line that passes through the points (x1,y1) and (x2,y2).
For the following problems, determine the slope and y-intercept of the lines.
y=4x+10
- Answer
-
slope: 4
y-intercept: (0,10)
y=3x−11
y=9x−1
- Answer
-
slope: 9
y-intercept: (0,−1)
y=−x+2
y=−5x−4
- Answer
-
slope: −5
y-intercept: (0,−4)
y=x
y=−6x
- Answer
-
slope: −6
y-intercept: (0,0)
3y=4x+9
4y=5x+1
- Answer
-
slope: 54
y-intercept: (0,14)
2y=9x
5y+4x=6
- Answer
-
slope: −45
y-intercept: (0,65)
7y+3x=10
6y−12x=24
- Answer
-
slope: 2
y-intercept: (0,4)
5y−10x−15=0
3y+3x=1
- Answer
-
slope: −1
y-intercept: (0,13)
7y+2x=0
y=4
- Answer
-
slope: 0
y-intercept: (0,4)
For the following problems, find the slope, if it exists, of the line through the given pairs of points.
(5,2),(6,3)
(8,−2),(10,−6)
- Answer
-
slope: −2
(0,5),(3,4)
(1,−4),(3,3)
- Answer
-
slope: 72
(0,0),(−8,−5)
(−6,1),(−2,7)
- Answer
-
slope: 32
(−3,−2),(−4,−5)
(4,7),(4,−2)
- Answer
-
No Slope
(−3,1),(4,1)
(13,34),(29,−56)
- Answer
-
slope: 574
Moving left to right, lines with slope rise while lines with slope decline.
Compare the slopes of parallel lines.
- Answer
-
The slopes of parallel lines are equal.
Finding the Equation of a Line
For the following problems, write the equation of the line using the given information. Write the equation in slope-intercept form.
Slope=4, y-intercept=5
Slope=3, y-intercept=−6
- Answer
-
y=3x−6
Slope=1, y-intercept=8
Slope=1, y-intercept=−2
- Answer
-
y=x−2
Slope=−5, y-intercept=1
Slope=−11, y-intercept=−4
- Answer
-
y=−11x−4
Slope=2, y-intercept=0
Slope=−1, y-intercept=0
- Answer
-
y=−x
m=3,(4,1)
m=2,(1,5)
- Answer
-
y=2x+3
m=6,(5,−2)
m=−5,(2,−3)
- Answer
-
y=−5x+7
m=−9,(−4,−7)
m=−2,(0,2)
- Answer
-
y=−2x+2
m=−1,(2,0)
(2,3),(3,5)
- Answer
-
y=2x−1
(4,4),(5,1)
(6,1),(5,3)
- Answer
-
y=−2x+13
(8,6),(7,2)
(−3,1),(2,3)
- Answer
-
y=25x+115
(−1,4),(−2,−4)
(0,−5),(6,−1)
- Answer
-
y=23x−5
(2,1),(6,1)
(−5,7),(−2,7)
- Answer
-
y=7 (zero slope)
(4,1),(4,3)
(−1,−1),(−1,5)
- Answer
-
x=−1 (no slope)
(0,4),(0,−3)
(0,2),(1,0)
- Answer
-
y=−2x+2
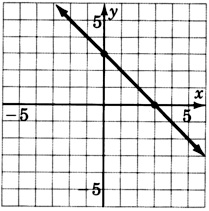
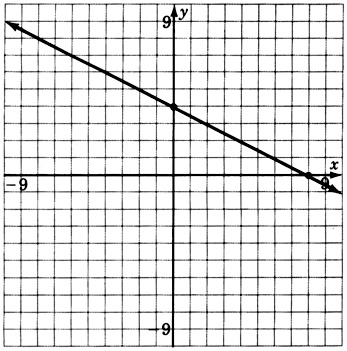
For the following problems, reading only from the graph, determine the equation of the line.
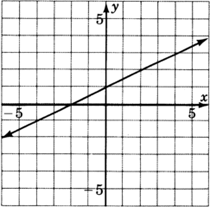
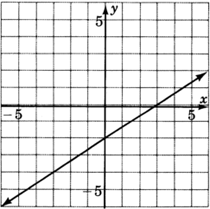
- Answer
-
y=23x−2
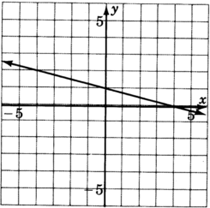
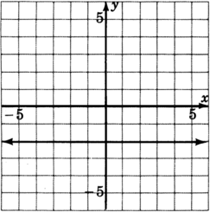
- Answer
-
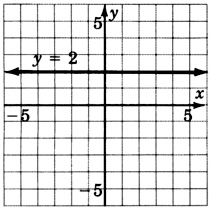
y=−2
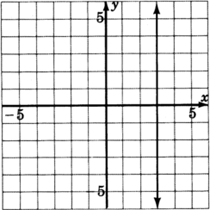
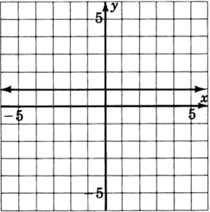
- Answer
-
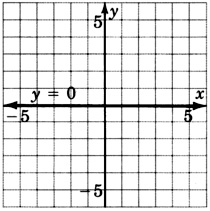
y=1
Graphing Linear Inequalities in Two Variables
For the following problems, graph the inequalities.
y≤x+2
y<−12+3

- Answer
-
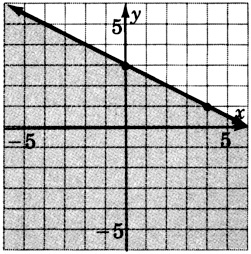
y>13x−3

−2x+3y≤−6

- Answer
-

2x+5y≥20

4x−y+12>0

- Answer
-
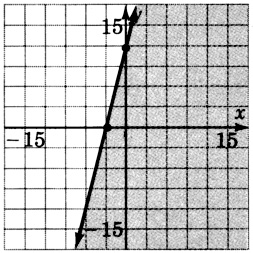
y≥−2

x<3

- Answer
-
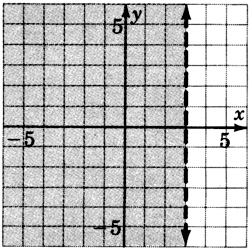
y≤0



