7.11: Proficiency Exam
- Page ID
- 60042
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Proficiency Exam
For the following problems, construct a coordinate system and graph the inequality.
\(−6x+4>−14\)
- Answer
-
\(x<3\)
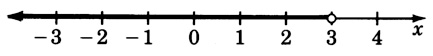
\(−8<x+6≤−4\)
- Answer
-
\(−14<x≤−10\)
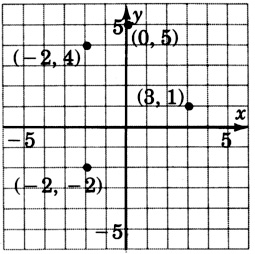
Plot the ordered pairs \((3, 1),(−2, 4),(0, 5),(−2, −2)\).
- Answer
-
As accurately as possible, label the coordinates of the points that have been plotted on the graph.
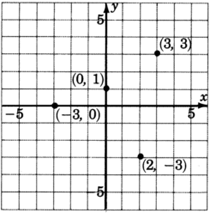
- Answer
-
\((0,1),(3,3),(−3,0),(2,−3)\)
What is the geometric structure of the graph of all the solutions to the equation \(2y+3x=−4\)?
- Answer
-
straight line
In what form is the linear equation in two variables \(ax+by=c\)?
- Answer
-
general form
In what form is the linear equation in two variables \(y=mx+b\)?
- Answer
-
slope-intercept
If an ordered pair is a solution to a linear equation in two variables, where does it lie geometrically?
- Answer
-
It lies on the line.
Consider the graph of \(y=\dfrac{2}{7}x+16\). If we were to place our pencil at any point on the line and then move it horizontally \(7\) units to the right, how many units and in what direction would we have to move our pencil to get back on the line?
- Answer
-
\(2\) units up
For the following problems, find the slope, if it exists, of the line containing the following points.
(−6, −1) and (0, 8)
- Answer
-
\(\dfrac{3}{2}\)
(−2, −8) and (−2, 10)
- Answer
-
no slope; vertical line at \(x=−2\)
Determine the slope and \(y\)−intercept of the line \(3y+2x+1=0\).
- Answer
-
slope = \(-\dfrac{2}{3}\), \(y\)-intercept is \((0, -\dfrac{1}{3})\)
As we look at a graph left to right, do lines with a positive slope rise or decline?
- Answer
-
rise
For the following problems, find the equation of the line using the information provided. Write the equation in slope-intercept form
Slope = \(4\), \(y\)-intercept = \(−3\).
- Answer
-
\(y=4x−3\)
Slope = \(-\dfrac{3}{2}\), \(y\)-intercept = \(\dfrac{4}{3}\).
- Answer
-
\(y = -\dfrac{3}{2}x + \dfrac{4}{3}\)
Slope = \(\dfrac{2}{3}\), passes through \((-1, 2)\)
- Answer
-
\(y = \dfrac{2}{3}x + \dfrac{8}{3}\)
Slope = \(7\), passes through \((0, 0)\)
- Answer
-
\(y=7x\)
Passes through the points \((5, 2)\) and \((2, 1)\).
- Answer
-
\(y = \dfrac{1}{3}x + \dfrac{1}{3}\)
For the following problems, graph the equation of inequality.
\(y = \dfrac{1}{3}x - 2\)
- Answer
-
\(y = \dfrac{1}{3}x - 2\)
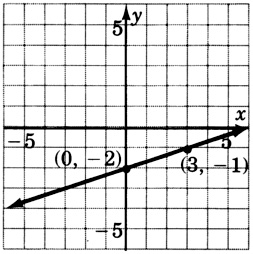
\(5y−2x+15=0\)
- Answer
-
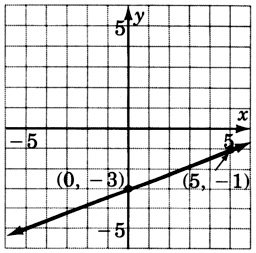
\(4(x+y)=8\)
- Answer
-
\(4(x+y)=8\)
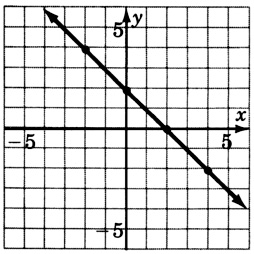
\(\dfrac{3}{2}y + 2 = 0\)
- Answer
-
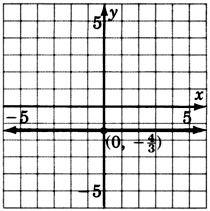
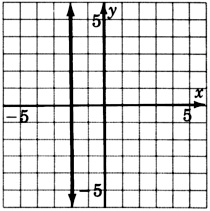
\(x=−2\)
- Answer
-
\(x=−2\)
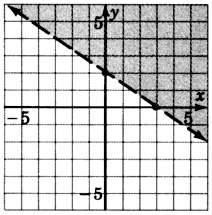
\(2x+3y>6\)
- Answer
-
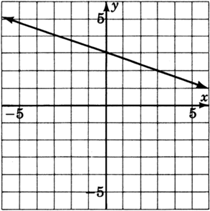
Reading only from the graph, determine the equation of the line.
- Answer
-
\(y = -\dfrac{1}{3}x + 3\)