10.7: Applications
- Page ID
- 49407
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Five-Step Method
We are now in a position to study some applications of quadratic equations. Quadratic equations can arise from a variety of physical (applied) and mathematical (logical) problems.
We will, again, apply the five-step method for solving word problems.
- Step 1: Let \(x\) (or some other letter) represent the unknown quantity.
- Step 2: Translate the verbal expression to mathematical symbols and form an equation.
- Step 3: Solve this equation.
- Step 4: Check the solution by substituting the result into the equation found in step 2.
- Step 5: Write a conclusion.
Remember, step 1 is very important.
Always start by introducing a variable
Once the quadratic equation is developed (step 2), try to solve it by factoring. If factoring doesn't work, use the quadratic formula. A calculator may help to make some of the calculations a little less tedious.
Sample Set A
A producer of personal computer mouse covers determines that the number \(N\) of covers sold is related to the price \(x\) of a cover by \(N = 35x - x^2\). At what price should the producer price a mouse in order to sell \(216\) of them.
\(\begin{array}{flushleft}
\text{Step 1: } & \text{Let } x= \text{ the price of a mouse cover.}\\
\text{Step 2: } & \text{Since } N \text{ is to be } 216 \text{, the equation is }\\
& 216 = 35x - x^2
\end{array}\)
\(\begin{array}{flushleft}
\text{Step 3: } & 216 &= 35x - x^2 & \text{ Rewrite in standard form }\\
& x^2 - 35x + 216 &= 0 & \text{ Try factoring. }\\
& (x-8)(x-27) &= 0\\
& x-8 = 0 & \text{ or } x-27=0 \\
& x = 8 & \text{ or } x=27
\end{array}\)
Check these potential solutions.
\(\begin{array}{flushleft}
\text{Step 4: } & \text{If } x=8, & & & \text{If } x = 27\\
& 35 \cdot 8 &= 216 & \text{ Is this correct? } & 35 \cdot 27 - 27^2 &= 216 & \text{ Is this correct? }\\
& 280 - 64 &= 216 & \text{ Is this correct? } & 945 - 729 &= 216 & \text{ Is this correct? }\\
& 216 &= 216 & \text{ Yes, this is correct. } & 216 &= 216 & \text{ Yes, this is correct. }\\
\end{array}\)
These solutions check.
Step 5: The computer mouse covers can be priced at either $8 or $27 in order to sell 216 of them.
Practice Set A
A manufacturer of cloth personal computer dust covers notices that the number \(N\) of covers sold is related to the price of covers by \(N = 30x - x^2\). At what price should the manufacturer price the covers in order to sell \(216\) of them?
Step 1:
Step 2:
Step 3:
Step 4:
Step 5: In order to sell 216 covers, the manufacturer should price them at either or .
- Answer
-
12 or 18
It is estimated that \(t\) years from now the population of a particular city will be
\(P = t^2 - 24t + 96000\)
How many years from now will the population by 95,856?
Step 1:
Step 2:
Step 3:
Step 4:
Step 5:
- Answer
-
In 9 and 15 years, the population of the city will be 95,865.
Sample Set B
The length of a rectangle is 4 inches more than twice its width. The area is 30 square inches. Find the dimensions (length and width).
Step 1: Let \(x=\) the width. Then, \(2x + 4 = \) the length.
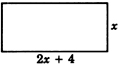
Step 2: The area of a is defined to be the length of the rectangle times the width of the rectangle. Thus,
\(x(2x + 4) = 30\)
\(\begin{array}{flushleft}
\text{Step 3: } & x(2x + 4) &= 30\\
& 2x^2 + 4x &= 30\\
& 2x^2 + 4x - 30 &= 0 & \text{ Divide each side by } 2\\
& x^2 + 2x - 15 &= 0 & \text{ Factor. }\\
& (x+5)(x-3) &= 0
& x &= -5, 3\\
& x & -5 & \text{ has no physical meaning so we disregard it. Check } x=3\\
& x &= 3
\end{array}\)
\(2x + 4 = 2 \cdot 3 + 4 = 10\)
\(\begin{array}{flushleft}
\text{Step 4: } & x(2x + 4) &= 30 & \text{Is this correct?}\\
& 3(2 \cdot 3 + 4) &= 30 & \text{Is this correct?}\\
& 3(6 + 4) &= 30 & \text{Is this correct?}\\
& 3(10) &= 30 & \text{Is this correct?}\\
& 30 &= 30 & \text{Yes, this is correct}
\end{array}\)
Step 5: Width \(= 3\) inches and length \(= 10\) inches.
Practice Set B
The length of a rectangle is 3 feet more than twice its width. The area is 14 square feet. Find the dimensions.
- Answer
-
width = 2 feet, length = 7 feet
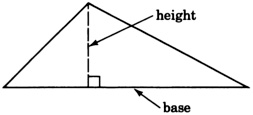
The area of a triangle is 24 square meters. The base is 2 meters longer than the height. Find the base and height. The formula for the area of a triangle is \(A = \dfrac{1}{2} b \cdot h\).
- Answer
-
height = 6 meters, base = 8 meters
Sample Set C
The product of two consecutive integers is 156. Find them
\(\begin{array}{flushleft}
\text{Step 1: } & \text{Let } x &= \text{ the smaller integer.}\\
& x + 1 &= \text{ the next integer}\\
\text{Step 2: } x(x + 1) &= 156\\
\text{Step 3: } x(x + 1) &= 156\\
& x^2 + x &= 156\\
& x^2 + x - 156 &= 0\\
& (x-12)(x - 13) &= 0\\
& x &= 12, -13
\end{array}\)
This factorization may be hard to guess. We could also have used the quadratic formula.
\(\begin{array}{flushleft}
\text{Step 4: } & \text{If } x=12: & 12(2 + 1) &= 156 & \text{Is this correct?}\\
& & 12(13) &= 156 & \text{Is this correct?}\\
& & 156 &= 156 & \text{Yes, this is correct}\\
& \text{If } x=-13 & -13(-13 + 1) &= 156 & \text{Is this correct?}\\
& & -13(-12) &= 156 & \text{Is this correct?}\\
& & 156 &= 156 & \text{Yes, this is correct.}
\end{array}\)
Step 5: There are two solutions: \(12, 13\), and \(-13, -12\)
Practice Set C
The product of two consecutive integers is 210. Find them.
- Answer
-
14 and 15, and –14 and –15
Four is added to an integer and that sum is tripled. When this result is multiplied by the original integer, the product is −12. Find the integer.
- Answer
-
–2
Sample Set D
A box with no top and a square base is to be made by cutting out 2-inch squares from each corner and folding up the sides of a piece of square cardboard. The volume of the box is to be 8 cubic inches. What size should the piece of cardboard be?
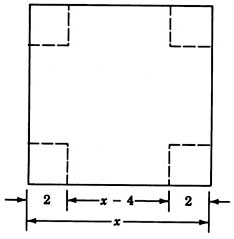
Step 1: Let \(x=\) the length (and width) of the piece of cardboard.
Step 2: The volume of a rectangular box is
\(V = \text{(length) (width) (height)}\)
\(8 = (x-4)(x-4)2\)
\(\begin{array}{flushleft}
\text{Step 3: } & 8=(x-4)(x-4)2\\
& 8=(x^2 - 8x + 16)2\\
& 8=2x^2 - 16x + 32\\
& 2x^2 - 16x + 24 = 0 & \text{Divide each side by } 2\\
& x^2 - 8x + 12 = 0 & \text{Factor.}\\
& (x-6)(x-2) = 0
& x = 6, 2
\end{array}\)
\(x\) cannot equal \(2\) (the cut would go through the piece of cardboard). Check \(x = 6\).
\(\begin{array}{flushleft}
\text{Step 4: } & (6 - 4)(6 - 4)2 &= 8 & \text{Is this correct?}\\
& (2)(2)2 &= 8 & \text{Is this correct?}\\
& 8&=8 & \text{Yes, this is correct.}
\end{array}\)
Step 5: The piece of cardboard should be 6 inches by 6 inches.
Practice Set D
A box with no top and a square base is to be made by cutting 3-inch squares from each corner and folding up the sides of a piece of cardboard. The volume of the box is to be 48 cubic inches. What size should the piece of cardboard be?
- Answer
-
10 in. by 10 in.; 2 by 2 is not physically possible.
Sample Set E
A study of the air quality in a particular city by an environmental group suggests that \(t\) years from now the level of carbon monoxide, in parts per million, in the air will be
\(A = 0.3t^2 + 0.1t + 4.2\)
a) What is the level, in parts per million, of carbon monoxide in the air now?
Since the equation \(A = 0.3t^2 + 0.1t + 4.2\) specifies the level \(t\) years from now, we have \(t = 0\).
\(A = 0.3t^2 + 0.1t + 4.2\\
A = 4.2\)
b) How many years from now will the level of carbon monoxide be at 8 parts per million?
\(\begin{array}{flushleft}
\text{Step 1: } & t &= \text{the number of yeras when the level is } 8\\
\text{Step 2: } & 8 &= 0.3t^2 + 0.1t + 4.2\\
\text{Step 3: } & 8 &= 0.3t^2 + 0.1t + 4.2\\
& 0 &= 0.3t^2 + 0.1t - 3.8 & \text{ This does not readily factor, so we'll use the quadratic formula. }\\
& a &= 0.3, b = 0.1, c = -3.8\\
& t &= \dfrac{-0.1 \pm \sqrt{(0.1)^2 = 4(0.3)(-3.8)}}{2(0.3)}\\
& &= \dfrac{-0.1 \pm \sqrt{0.01 + 4.56}}{0.6} = \dfrac{-0.1 \pm \sqrt{4.57}}{0.6}\\
& &= \dfrac{-0.1 \pm 2.14}{0.6}\\
& t &= 3.4 \text{ and } -3.73
\end{array}\)
\(t = -3.73\) has no physical meaning. Check \(t = 3.4\)
Step 4: This value of \(t\) has been rounded to the nearest tenth. It does check (pretty closely).
Step 5: About 3.4 years from now the carbon monoxide level will be \(8\).
Practice Set E
A study of the air quality in a particular city by an environmental group suggests that t years from now the level of carbon monoxide, in parts per million, in the air will be
\(A = 0.2t^2 + 0.1t + 5.1\)
a) What is the level, in parts per million, now?
b) How many years from now will the level of carbon monoxide be at 8 parts per million? Round to the nearest tenth.
- Answer
-
(a). 5.1 parts per million
(b). 3.6 years
Sample Set F
A contractor is to pour a concrete walkway around a swimming pool that is 20 feet wide and 40 feet long. The area of the walkway is to be 544 square feet. If the walkway is to be of uniform width, how wide should the contractor make it?
Step 1: Let \(x=\) the width of the walkway.
Step 2: A diagram will help us to get the equation
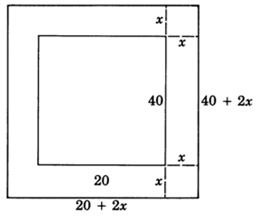
(Area of pool and walkway) - (Area of pool) = (area of walkway)
\((20 + 2x)(40 + 2x) - 20 \cdot 40 = 544\)
\(\begin{array}{flushleft}
\text{Step 3: } & (20 + 2x)(40 + 2x) - 20 \cdot 40 &= 544\\
& 800 + 120x + 4x^2 - 800 &= 544\\
& 120x + 4x^23 &= 544\\
& 4x^2 + 120x - 544 &= 0 & \text{Divide each term by } 4\\
& x^2 + 30x - 136 &= 0 & \text{Solve by factoring. (or quadratic formula) }\\
& (x-4)(x + 34) &= 0
\end{array}\)
\(\begin{array}{flushleft}
x - 4 &= 0 & \text{ or } & x + 34 &= 0\\
x &=4 & \text{ or } & x &= -34 \text{ has no physical meaning}
\end{array}\)
Check a width of 4 feet as a solution.
\(\begin{array}{flushleft}
\text{Step 4: } & \text{Area of pool and walkway } &= (20 + 2 \cdot 4)(40 + 2 \cdot 4)\\
& &= (28)(48)\\
& &= 1344
\end{array}\)
Area of pool \(=(20)(40) = 800\)
Area of walkway \(=1344 - 800 = 544\). Yes, this is correct.
This solution checks.
Step 5: The contractor should make the walkway 4 feet wide.
Practice Set F
A contractor is to pour a concrete walkway around a swimming pool that is 15 feet wide and 25 feet long. The area of the walkway is to be 276 square feet. If the walkway is to be of uniform width, how wide should the contractor make it?
- Answer
-
3 ft wide
Exercises
Some of the following problems have actual applications and some are intended only as logic developers. A calculator may be helpful. The problems appear in groups and correspond to the noted Sample Set problem.
Sample Set A—Type Problems
The manufacturer of electronic fuel injectors determines that the number \(N\) of injectors sold is related to the price \(x\) per injector by \(N = 22x - x^2\). At what price should the manufacturer price the injectors so that 112 of them are sold?
- Answer
-
$8 or $14
The owner of a stained-glass shop determines that the number \(N\) of pieces of a particular type of glass sold in a month is related to the price \(x\) per piece by \(N = 21x - x^2\). At what price should the shop buyer price the glass so that 162 sells?
It is estimated that \(t\) years from now the population of a certain city will be
\(P = t^2 - 15t + 12036\)
a) What is the population now?
b) How many years from now will the population be 12,000?
- Answer
-
(a) 12,036
(b) 3 and 12 years from now
It is estimated that \(t\) years from now the population of a certain city will be
\(P = t^2 - 16t + 24060\)
a) What is the population now?
b) How many years from now will the population be 24,000?
If an object is thrown vertically upward, its height \(h\), above the ground, in feet, after \(t\) seconds is given by \(h = h_0 + v_0t - 16t^2\), where \(h_0\) is the initial height from which the object is thrown and \(v_0\) is the initial velocity of the object. Using this formula and an approach like that of Sample Set A, solve this problem.
A ball thrown vertically into the air has the equation of motion \(h = 48 + 32t - 16t^2\).
a) How high is the ball at \(t = 0\) (the initial height of the ball)?
b) How high is the ball at \(t = 1\) (after 1 second in the air)?
c) When does the ball hit the ground? (Hind: Determine the appropriate value for \(h\) then solve for \(t\) ).
- Answer
-
(a) 48 feet
(b) 64 feet
(c) \(t = 3\)
A woman's glasses accidentally fall off her face while she is looking out of a window in a tall building. The equation relating \(h\), the height above the ground in feet, and \(t\), the time ins seconds her glasses have been falling, is \(h = 64 - 16t^2\).
a) How high was the woman’s face when her glasses fell off?
b) How many seconds after the glasses fell did they hit the ground?
Sample Set B—Type Problems
The length of a rectangle is 6 feet more than twice its width. The area is 8 square feet. Find the dimensions.
- Answer
-
length=8; width=1
The length of a rectangle is 18 inches more than three times its width. The area is 81 square inches. Find the dimensions.
The length of a rectangle is two-thirds its width. The area is 14 square meters. Find the dimensions.
- Answer
-
width = \(\sqrt{21}\); length = \(\dfrac{2}{3} \sqrt{21}\)
The length of a rectangle is four-ninths its width. The area is 144 square feet. Find the dimensions.
The area of a triangle is 14 square inches. The base is 3 inches longer than the height. Find both the length of the base and height.
- Answer
-
\(b=7; h=4\)
The area of a triangle is 34 square centimeters. The base is 1 cm longer than twice the height. Find both the length of the base and the height
Sample Set C—Type Problems
The product of two consecutive integers is 72. Find them.
- Answer
-
−9,−8 or 8,9
The product of two consecutive negative integers is 42. Find them.
The product of two consecutive odd integers is 143. Find them. (Hint: The quadratic equation is factorable, but the quadratic formula may be quicker.)
- Answer
-
−13,−11 or 11,13
The product of two consecutive even integers is 168. Find them.
Three is added to an integer and that sum is doubled. When this result is multiplied by the original integer the product is 20. Find the integer.
- Answer
-
\(n=2,−5\)
Four is added to three times an integer. When this sum and the original integer are multiplied, the product is −1. Find the integer.
Sample Set D—Type Problems
A box with no top and a square base is to be made by cutting out 2-inch squares from each corner and folding up the sides of a piece of cardboard. The volume of the box is to be 25 cubic inches. What size should the piece of cardboard be?
- Answer
-
\(4 + \sqrt{12.5}\) inches
A box with no top and a square base is to made by cutting out 8-inch squares from each corner and folding up the sides of a piece of cardboard. The volume of the box is to be 124 cubic inches. What size should the piece of cardboard be?
Sample Set E—Type Problems
A study of the air quality in a particular city by an environmental group suggests that \(t\) years from now the level of carbon monoxide, in parts per million, will be \(A = 0.1t^2 + 0.1t + 2.2\).
a) What is the level, in parts per million, of carbon monoxide in the air now?
b) How many years from now will the level of carbon monoxide be at 3 parts per million?
- Answer
-
(a) carbon monoxide now 2.2 parts per million
(b) 2.37 years
A similar study to that of problem 21 suggests \(A = 0.3t^2 + 0.25t + 3.0\)
a) What is the level, in parts per million, of carbon monoxide in the air now?
b) How many years from now will the level of carbon monoxide be at 3 parts per million?
Sample Set F—Type Problems
A contractor is to pour a concrete walkway around a wading pool that is 4 feet wide and 8 feet long. The area of the walkway and pool is to be 96 square feet. If the walkway is to be of uniform width, how wide should it be?
- Answer
-
\(x=2\)
Astrophysical Problem
A very interesting application of quadratic equations is determining the length of a solar eclipse (the moon passing between the earth and sun). The length of a solar eclipse is found by solving the quadratic equation
\((a + bt)^2 + (c + dt)^2 = (e + ft)^2\)
for \(t\). The letters \(a, b, c, d, e\), and \(f\) are constants that pertain to a particular eclipse. The equation is a quadratic equation in \(t\) and can be solved by the quadratic formula (and definitely a calculator). Two values of \(t\) will result. The length of the eclipse is just the difference of these \(t\)-values.
The following constants are from a solar eclipse that occurred on August 3, 431 B.C.
\(\begin{array}{flushleft}
a &= -619 & b &= 1438\\
c &= 912 & d &= -833\\
e &= 1890.5 & f&=-2
\end{array}\)
Determine the length of this particular solar eclipse.
Exercises For Review
Find the sum: \(\dfrac{2x + 10}{x^2 + x - 2} + \dfrac{x + 3}{x^2 - 3x + 2}\)
- Answer
-
\(\dfrac{3x + 14}{(x+2)(x-2)}\)
Solve the fractional equation \(\dfrac{4}{x+12} + \dfrac{3}{x + 3} = \dfrac{4}{x^2 + 5x + 6}\)
(Hint: Check for extraneous solutions)
One pipe can fill a tank in 120 seconds and another pipe can fill the same tank in 90 seconds. How long will it take both pipes working together to fill the tank?
- Answer
-
\(51 \dfrac{3}{7}\)
Use the quadratic formula to solve \(10x^2 - 3x - 1 = 0\)
Use the quadratic formula to solve \(4x^2 - 3x = 0\)
- Answer
-
\(x = 0, \dfrac{3}{4}\)


