10.8: Graphing Quadratic Solutions

Last updated
Save as PDF

Page ID: 49408

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Parabolas

We will now study the graphs of quadratic equations in two variables with general form

$y = ax^2 + bx + c, a \not= 0$. $a, b, c$ are real numbers.

Parabola

All such graphs have a similar shape. The graph of a quadratic equation of this type Parabola is called a parabola and it will assume one of the following shapes.

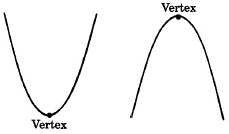
$Two parabolas, one opening upward and one opening downward. The lowest point of the parabola opening upward and the highest point of the parabola opening downward are each labeled as 'Vertex.'$

Vertex

The high point or low point of a parabola is called the vertex of the parabola.

Constructing Graphs of Parabolas

We will construct the graph of a parabola by choosing several x-values, computing to find the corresponding y-values, plotting these ordered pairs, then drawing a smooth curve through them.

Sample Set A

Example $\PageIndex{1}$

Graph $y = x^2$. Construct a table to exhibit several ordered pairs.

$x$	$y=x^2$
0	0
1	1
2	4
3	9
−1	1
−2	4
−3	9

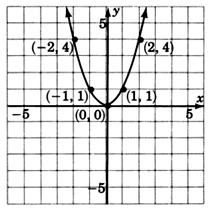
$A graph of a parabola passing through five points with coordinates negative two, four; negative one, one; zero, zero; one, one; and two, four.$

This is the most basic parabola. Although other parabolas may be wider, narrower, moved up or down, moved to the left or right, or inverted, they will all have this same basic shape. We will need to plot as many ordered pairs as necessary to ensure this basic shape.

Example $\PageIndex{2}$

Graph $y = x^2 - 2$. Construct a table of ordered pairs.

$x$	$y=x^2 -2$
0	−2
1	−1
2	2
3	7
−1	−1
−2	2
−3	7

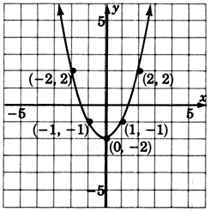
$A graph of a parabola passing through five points with coordinates negative two, two; negative one , negative one; zero, negative two, one, negative one; and two, two.$

Notice that the graph of $y = x^2 - 2$ is precisely the graph of $y = x^2$ but translated 2 units down. Compare the equations of $y = x^2$ and $y = x^2 - 2$. Do you see what causes the 2 unit downward translation?

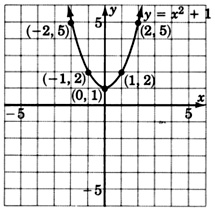
Practice Set A

Practice Problem $\PageIndex{1}$

Use the idea suggested in Sample Set A to sketch (quickly and perhaps not perfectly accurately) the graphs of

$y = x^2 + 1$ and $y = x^2 - 3$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one units on both axes.$

Answer

$A graph of a quadratic equation y equals x square plus one passing through five points with coordinates negative two, five; negative one, two; zero, one; one, two; and two, five.$

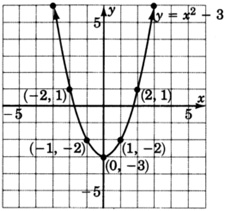
$A graph of a quadratic equation y equals x square minus three passing through five points with coordinates negative two, one; negative one, negative two; zero, negative three; one, negative two; and two, one.$

Sample Set B

Example $\PageIndex{1}$

Graph $y = (x + 2)^2$.

Do we expect the graph to be similar to the graph of $y = x^2$? Make a table of ordered pairs.

$x$	$y$
0	4
1	9
−1	1
−2	0
−3	1
−4	4

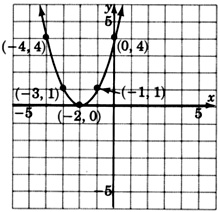
$A graph of a parabola passing through five points with coordinates negative four, four; negative three, one; negative two, zero;negative one, one; and zero, four.$

Notice that the graph of $y = (x + 2)^2$ is precisely the graph of $y = x^2$ but translated 2 units to the left. The $+2$ inside the parentheses moves $y = x^2$ two units to the left. A negative value inside the parentheses makes a move to the right.

Practice Set B

Practice Problem $\PageIndex{1}$

Use the idea suggested in Sample Set B to sketch the graphs of

$y = (x-3)^2$ and $y = (x + 1)^2$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one units on both axes.$

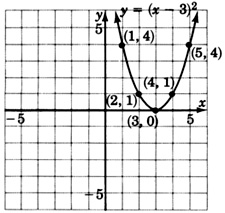
Answer: $A graph of a quadratic equation y equals x minus three the whole square passing through five points with the coordinates one, four; two, one; three, zero; four, one; and five, four.$

Practice Problem $\PageIndex{3}$

Graph $y = (x-2)^2 + 1$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one units on both axes.$

Answer: $A graph of a quadratic equation y equals x square minus three passing through five points with the coordinates zero, five; one, two; two, one; three, two; and four, five.$

Exercises

For the following problems, graph the quadratic equations.

Exercise $\PageIndex{1}$

$y = x^2$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one units on both axes.$

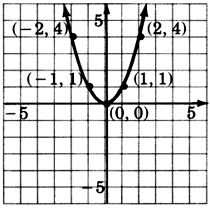
Answer: $A graph of a parabola passing through five points with coordinates negative two, four; negative one, one; zero, zero, one, one; and two, four.$

Exercise $\PageIndex{2}$

$y = -x^2$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one units on both axes.$

Exercise $\PageIndex{3}$

$y = (x-1)^2$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one units on both axes.$

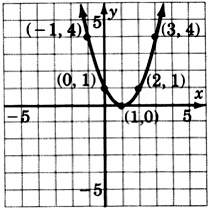
Answer: $A graph of a parabola passing through five points with coordinates negative one, four; zero, one; one, zero, two, one; and three, four.$

Exercise $\PageIndex{4}$

$y = (x-2)^2$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one units on both axes.$

Exercise $\PageIndex{5}$

$y = (x + 3)^2$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one units on both axes.$

Exercise $\PageIndex{6}$

$y = (x + 3)^2$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one units on both axes.$

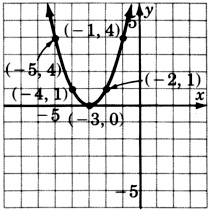
Answer: $A graph of a parabola passing through five points with coordinates negative five, four; negative four, one; negative three,zero; negative two, one; and negative one, four.$

Exercise $\PageIndex{7}$

$y = (x + 1)^2$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one units on both axes.$

Exercise $\PageIndex{8}$

$y = x^2 - 3$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one units on both axes.$

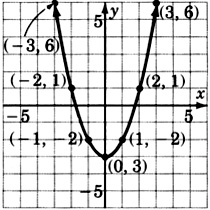
Answer: $A graph of a parabola passing through seven points with coordinates negative three, six; negative two, one; negative one, negative two; zero, negative three; one, negative two; two, one; and three, six.$

Exercise $\PageIndex{9}$

$y = x^2 - 1$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one units on both axes.$

Exercise $\PageIndex{10}$

$y = x^2 + 2$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one units on both axes.$

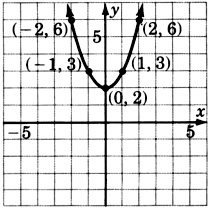
Answer: $A graph of a parabola passing through five points with coordinates negative two, six; negative one, three; zero, two; one, three; and two, six.$

Exercise $\PageIndex{11}$

$y = x^2 + \dfrac{1}{2}$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one units on both axes.$

Exercise $\PageIndex{12}$

$y = x^2 - \dfrac{1}{2}$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one units on both axes.$

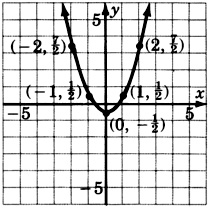
Answer: $A graph of a parabola passing through five points with coordinates negative two, seven over two; negative one, one over two; zero, negative one over two; one, one over two; and two, seven over two.$

Exercise $\PageIndex{13}$

$y = -x^2 + 1$ (compare with problem 2)

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one units on both axes.$

Exercise $\PageIndex{14}$

$y = -x^2 - 1$ (compare with problem 1)
$An xy coordinate plane with gridlines, labeled negative five and five with increments of one units on both axes.$

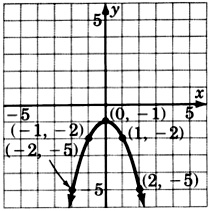
Answer: $A graph of a parabola passing through five points with coordinates negative two, negative five; negative one, negative two; zero, negative one, one, negative two; and two, negative five.$

Exercise $\PageIndex{15}$

$y = (x-1)^2 - 1$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one units on both axes.$

Exercise $\PageIndex{16}$

$y = (x + 3)^2 + 2$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one units on both axes.$

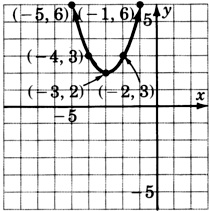
Answer: $A graph of a parabola passing through five points with coordinates negative five, six; negative four, three; negative three, two; negative two, three; and negative one, six.$

Exercise $\PageIndex{17}$

$y = -(x + 1)^2$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one units on both axes.$

Exercise $\PageIndex{18}$

$y = -(x + 3)^2$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one units on both axes.$

Answer: $A graph of a parabola passing through five points with coordinates negative five, negative four; negative four, negative one; negative three, zero; negative two, negative one; and negative one, negative four.$

Exercise $\PageIndex{19}$

$y = 2x^2$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one units on both axes.$

Exercise $\PageIndex{20}$

$y = 3x^2$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one units on both axes.$

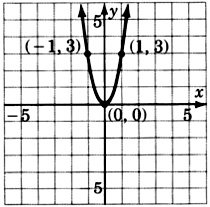
Answer: $A graph of a parabola passing through three points with coordinates negative one, three; zero, zero; and one, three.$

Exercise $\PageIndex{21}$

$y = \dfrac{1}{2}x^2$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one units on both axes.$

For the following problems, try to guess the quadratic equation that corresponds to the given graph.

Exercise $\PageIndex{22}$

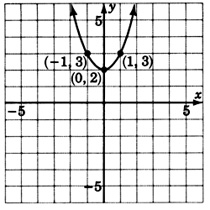
$A graph of a quadratic equation passing through three points with coordinates negative one, three; zero, two; and one, three.$

Exercise $\PageIndex{23}$

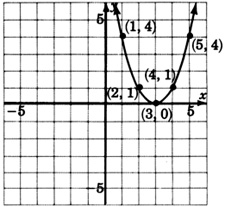
$A graph of a quadratic equation passing through three points with coordinates one, four; two, one; three, zero; four, one and five, four.$

Answer: $y = (x-3)^2$

Exercise $\PageIndex{24}$

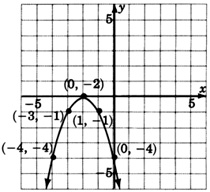
$A graph of a quadratic equation passing through five points with coordinates negative four, negative four; negative three, negative one; negative two, zero ;negative one, negative one; and zero, negative four.$

Exercise $\PageIndex{25}$

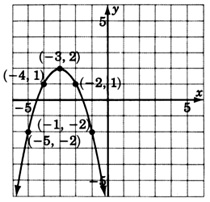
$A graph of a quadratic equation passing through five points with coordinates negative five, negative two; negative four, one; negative three, two;negative two, one; and negative one, negative two.$

Answer: $y = -(x + 3)^2 + 2$

Exercises For Review

Exercise $\PageIndex{26}$

Simplify and write $(x^{-4}y^5)^{-3}(x^{-6}y^4)^2$ so that only positive exponents appear.

Exercise $\PageIndex{27}$

Factor $y^2 - y - 42$

Answer: $(y+6)(y−7)$

Exercise $\PageIndex{28}$

Find the sum: $\dfrac{2}{a - 3} + \dfrac{3}{a + 3} + \dfrac{18}{a^2 - 9}$

Exercise $\PageIndex{29}$

Simplify $\dfrac{2}{4 + \sqrt{5}}$

Answer: $\dfrac{8 - 2\sqrt{5}}{11}$

Exercise $\PageIndex{30}$

Four is added to an integer and that sum is doubled. When this result is multiplied by the original integer, the product is $-6$. Find the integer.

Parabolas

Constructing Graphs of Parabolas

Sample Set A

Example \(\PageIndex{1}\)

Example \(\PageIndex{2}\)

Practice Set A

Practice Problem \(\PageIndex{1}\)

Sample Set B

Example \(\PageIndex{1}\)

Practice Set B

Practice Problem \(\PageIndex{1}\)

Practice Problem \(\PageIndex{3}\)

Exercises

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\)

Exercise \(\PageIndex{4}\)

Exercise \(\PageIndex{5}\)

Exercise \(\PageIndex{6}\)

Exercise \(\PageIndex{7}\)

Exercise \(\PageIndex{8}\)

Exercise \(\PageIndex{9}\)

Exercise \(\PageIndex{10}\)

Exercise \(\PageIndex{11}\)

Exercise \(\PageIndex{12}\)

Exercise \(\PageIndex{13}\)

Exercise \(\PageIndex{14}\)

Exercise \(\PageIndex{15}\)

Exercise \(\PageIndex{16}\)

Exercise \(\PageIndex{17}\)

Exercise \(\PageIndex{18}\)

Exercise \(\PageIndex{19}\)

Exercise \(\PageIndex{20}\)

Exercise \(\PageIndex{21}\)

Exercise \(\PageIndex{22}\)

Exercise \(\PageIndex{23}\)

Exercise \(\PageIndex{24}\)

Exercise \(\PageIndex{25}\)

Exercises For Review

Exercise \(\PageIndex{26}\)

Exercise \(\PageIndex{27}\)

Exercise \(\PageIndex{28}\)

Exercise \(\PageIndex{29}\)

Exercise \(\PageIndex{30}\)