14.6: Exercise

Last updated
Save as PDF

Page ID: 34266

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Skills

Counting Board And Quipu

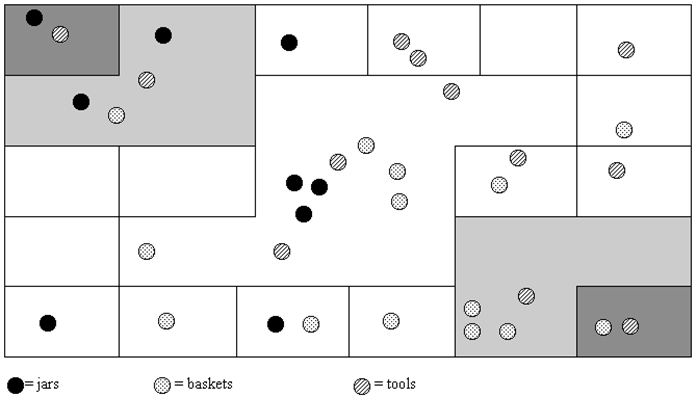
1) In the following Peruvian counting board, determine how many of each item is represented. Please show all of your calculations along with some kind of explanation of how you got your answer. Note the key at the bottom of the drawing.

$clipboard_e0c3bd0462129b752dac84432aaa0118a.png$

2) Draw a quipu with a main cord that has branches (H cords) that show each of the following numbers on them. (You should produce one drawing for this problem with the cord for part a on the left and moving to the right for parts b through d.)

a. 232	b. 5065
c. 23451	d. 3002

Basic Base Conversions

3) 423 in base 5 to base 10	4) 3044 in base 5 to base 10
5) 387 in base 10 to base 5	6) 2546 in base 10 to base 5
7) 110101 in base 2 to base 10	8) 11010001 in base 2 to base 10
9) 100 in base 10 to base 2	10) 2933 in base 10 to base 2
11) Convert 653 in base 7 to base 10	12) Convert 653 in base 10 to base 7
13) 3412 in base 5 to base 2	14) 10011011 in base 2 to base 5

(Hint: convert first to base 10 then to the final desired base)

The Caidoz System

Suppose you were to discover an ancient base-12 positional system made up twelve symbols. Let’s call this base system the Caidoz system. Here are the symbols for each of the numbers 0 through 12:

$clipboard_ee37224e1a84172c879dd825a1675837c.png$

Convert each of the following numbers in Caidoz to base 10

$clipboard_efb90ded3a486be54e3f82dbd093b307f.png$

Convert the following base 10 numbers to Caidoz, using the symbols shown above.

19) 175	20) 3030
21) 10000	22) 5507

Mayan Conversions

Convert the following numbers to Mayan notation. Show your calculations used to get your answers.

23) 135	24) 234
25) 360	26) 1215
27) 10500	28) 1100000

Convert the following Mayan numbers to decimal (base-10) numbers. Show all calculations.

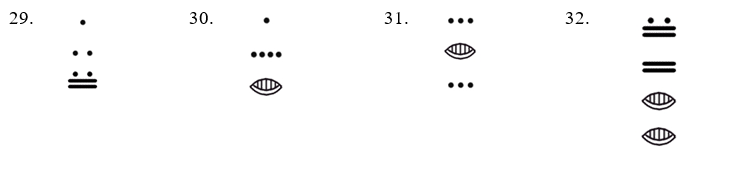
$clipboard_e8eebd940665c72ab21363bb7b9f6bc50.png$

James Bidwell has suggested that Mayan addition was done by “simply combining bars and dots and carrying to the next higher place.” He goes on to say, “After the combining of dots and bars, the second step is to exchange every five dots for one bar in the same position.” After converting the following base 10 numbers into vertical Maya notation (in base 20, of course), perform the indicated addition:

33) 32 + 11	34) 82 + 15
35) 35 + 148	36) 2412 + 5000
37) 450 + 844	38) 10000 + 20000
39) 4500 + 3500	40) 130000 + 30000

41) Use the fact that the Mayans had a base-20 number system to complete the following multiplication table. The table entries should be in Mayan notation. Remember: Their zero looked like this…. Xerox and then cut out the table below, fill it in, and paste it onto your homework assignment if you do not want to duplicate the table with a ruler.

(To think about but not write up: Bidwell claims that only these entries are needed for “Mayan multiplication.” What does he mean?)

Binary and Hexadecimal Conversions

Modern computers operate in a world of “on” and “off” electronic switches, so use a binary counting system – base 2, consisting of only two digits: 0 and 1.

Convert the following binary numbers to decimal (base-10) numbers.

42) 1001	43) 1101
44) 110010	45) 101110

Convert the following base-10 numbers to binary

46) 7	47) 12
48) 36	49) 27

Four binary digits together can represent any base-10 number from 0 to 15. To create a more human-readable representation of binary-coded numbers, hexadecimal numbers, base 16, are commonly used. Instead of using the 8,13,12₁₆ notation used earlier, the letter A is used to represent the digit 10, B for 11, up to F for 15, so 8,13,12₁₆ would be written as 8DC.

Convert the following hexadecimal numbers to decimal (base-10) numbers.

50) C3	51) 4D
52) 3A6	53) BC2

Convert the following base-10 numbers to hexadecimal

54) 152	55) 176
56) 2034	57) 8263

Exploration

58) What are the advantages and disadvantages of bases other than ten.

59) Supposed you are charged with creating a base-15 number system. What symbols would you use for your system and why? Explain with at least two specific examples how you would convert between your base-15 system and the decimal system.

60) Describe an interesting aspect of Mayan civilization that we did not discuss in class. Your findings must come from some source such as an encyclopedia article, or internet site and you must provide reference(s) of the materials you used (either the publishing information or Internet address).

61) For a Papuan tribe in southeast New Guinea, it was necessary to translate the bible passage John 5:5 “And a certain man was there, which had an infirmity 30 and 8 years” into “A man lay ill one man, both hands, five and three years.” Based on your own understanding of bases systems (and some common sense), furnish an explanation of the translation. Please use complete sentences to do so. (Hint: To do this problem, I am asking you to think about how base systems work, where they come from, and how they are used. You won’t necessarily find an “answer” in readings or such…you’ll have to think it through and come up with a reasonable response. Just make sure that you clearly explain why the passage was translated the way that it was.)

62) The Mayan calendar was largely discussed leading up to December 2012. Research how the Mayan calendar works, and how the counts are related to the number based they use.

Search

Text Color

Text Size

Margin Size

Font Type