16.5: Public Key Cryptography

Suppose that you are connecting to your bank’s website. It is possible that someone could intercept any communication between you and your bank, so you’ll want to encrypt the communication. The problem is that all the encryption methods we’ve discussed require than both parties have already agreed on a shared secret encryption key. How can you and your bank agree on a key if you haven’t already?

This becomes the goal of public key cryptography – to provide a way for two parties to agree on a key without a snooping third party being able to determine the key. The method relies on a one-way function; something that is easy to do one way, but hard to reverse. We will explore the Diffie-Hellman-Merkle key exchange method.

As an example, let’s consider mixing paint. It’s easy to mix paint to make a new color, but much harder to separate a mixed paint into the two original colors used.[1][2]

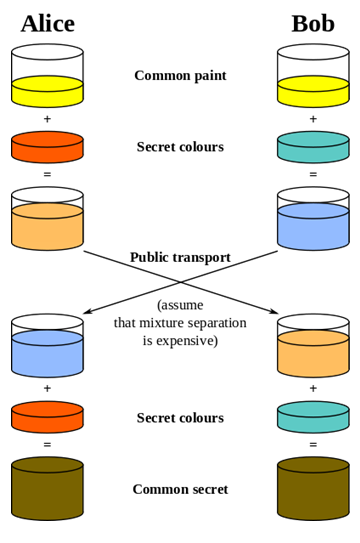Using this analogy, Alice and Bob publically agree on a common starter color. Each then mixes in some of their own secret color. They then exchange their mixed colors.

Since separating colors is hard, even if a snooper were to obtain these mixed colors, it would be hard to obtain the original secret colors.

Once they have exchanged their mixed colors, Alice and Bob both add their secret color to the mix they obtained from the other person. In doing so, both Alice and Bob now have the same common secret color, since it contains a mix of the original common color, Alice’s secret color, and Bob’s secret color.

They now have a common secret color they can use as their encryption key, even though neither Alice nor Bob knows the other’s secret color.

Likewise, there is no way for a snooper to obtain the common secret color without separating one of the mixed colors.

To get this process to work for computer communication, we need to have the process result in a share common number to act as the common secret encryption key. For this, we need a numerical one-way function.

Modular arithmetic

If you think back to doing division with whole numbers, you may remember finding the whole number result and the remainder after division.

Modulus[3]

The modulus is another name for the remainder after division.

For example, 17 mod 5 = 2, since if we divide 17 by 5, we get 3 with remainder 2.

Modular arithmetic is sometimes called clock arithmetic, since analog clocks wrap around times past 12, meaning they work on a modulus of 12. If the hour hand of a clock currently points to 8, then in 5 hours it will point to 1. While \(8+5 = 13\), the clock wraps around after 12, so all times can be thought of as modulus 12. Mathematically, 13 mod 12 = 1.

Example 11

Compute: a) 10 mod 3 b) 15 mod 5 c) \(2^{7}\) mod 5

Solution

a) Since 10 divided by 3 is 3 with remainder 1,10 mod \(3=1\)

b) Since 15 divided by 5 is 3 with no remainder, 15 mod \(5=0\)

c) \(2^{7}=128.128\) divide by 5 is 25 with remainder \(3,\) so \(2^{7}\) mod \(5=3\)

Try it Now 5

Compute: a) 23 mod 7 b) 15 mod 7 c) 2034 mod 7

Answer

a) 2 b) 1 c) 4

Recall that when we divide 17 by 5, we could represent the result as 3 remainder 2, as the mixed number \(3\frac{2}{5}\), or as the decimal 3.4. Notice that the modulus, 2, is the same as the numerator of the fractional part of the mixed number, and that the decimal part 0.4 is equivalent to the fraction . We can use these conversions to calculate the modulus of not-too-huge numbers on a standard calculator.

Modulus on a Standard Calculator

To calculate \(a\) mod \(n\) on a standard calculator

1. Divide \(a\) by \(n\)
2. Subtract the whole part of the resulting quantity
3. Multiply by \(n\) to obtain the modulus

Example 12

Calculate 31345 mod 419

Solution

\(\begin{array}{ll} 31345 / 419=74.8090692 & \text{Now subtract 74 to get just the decimal remainder} \\ 74.8090692-74=0.8090692 & \text{Multiply this by 419 to get the modulus} \\ 0.8090692 \times 419=339 & \text{This tells us 0.8090692 was equivalent to }\frac{339}{419} \end{array}\)

In the text above, only a portion of the decimal value was written down. In practice, you should try to avoid writing down the intermediary steps, and instead allow your calculator to retain as many decimal values as it can.

The one-way function

When you use a prime number \(p\) as a modulus, you can find a special number called a generator, \(g,\) so that \(g^{n}\) mod \(p\) will result in all the values from 1 to \(p-1\)

\(\begin{array}{|l|l|l|}
\hline n & 3^{n} & 3^{n} \mathrm{mod} 7 \\
\hline 1 & 3 & 3 \\
\hline 2 & 9 & 2 \\
\hline 3 & 27 & 6 \\
\hline 4 & 81 & 4 \\
\hline 5 & 243 & 5 \\
\hline 6 & 729 & 1 \\
\hline
\end{array}\)

In the table to the top, notice that when we give values of \(n\) from 1 to \(6,\) we get out all values from 1 to \(6 .\) This means 3 is a generator when 7 is the modulus.

This gives us our one-way function. While it is easy to compute the value of \(g^{n}\) mod \(p\) when we know \(n\), it is difficult to find the exponent \(n\) to obtain a specific value.

For example, suppose we use \(p=23\) and \(g=5 .\) If I pick \(n\) to be \(6,\) I can fairly easily calculate \(5^{6}\) mod \(23=15625\) mod \(23=8\)

If someone else were to tell you \(5^{n} \bmod 23=7\), it is much harder to find \(n\). In this particular case, we’d have to try 22 different values for \(n\) until we found one that worked – there is no known easier way to find \(n\) other than brute-force guessing.

While trying 22 values would not take too long, when used in practice much larger values for \(p\) are used, typically with well over 500 digits. Trying all possibilities would be essentially impossible.

The key exchange

Before we can begin the key exchange process, we need a couple more important facts about modular arithmetic.

Modular Exponentialtion Rule

\(\left(a^{b} \bmod n\right)=(a \bmod n)^{b} \bmod n\)

Example 13

Compute \(12^{5}\) mod 7 using the exponentiation rule.

Solution

Evaluated directly: \(12^{5}=248,832,\) so \(12^{5}\) mod \(7=248,823\) mod \(7=3\)

Using the rule above, \(12^{5}\) mod \(7=(12 \bmod 7)^{5} \bmod 7=5^{5} \bmod 7=3125 \bmod 7=3\)

You may remember a basic exponent rule from algebra:

\[\left(a^{b}\right)^{c}=a^{b c}=a^{c b}=\left(a^{c}\right)^{b} \nonumber \]

For example:

\[64^{2}=\left(4^{3}\right)^{2}=4^{6}=\left(4^{2}\right)^{3}=16^{3} \nonumber \]

We can combine the modular exponentiation rule with the algebra exponent rule to define the modular exponent power rule.

Modular Exponent Power Rule

\[\left(a^{b} \bmod n\right)^{c} \bmod n=\left(a^{b c} \bmod n\right)=\left(a^{c} \bmod n\right)^{b} \bmod n \nonumber \]

Example 14

Verify the rule above if \(a=3, b=4, c=5,\) and \(n=7\)

Solution

\(\left(3^{4} \bmod 7\right)^{5} \bmod 7=(81 \bmod 7)^{5} \bmod 7=4^{5} \bmod 7=1024 \bmod 7=2\)

\(\left(3^{5} \bmod 7\right)^{4} \bmod 7=(243 \bmod 7)^{4} \bmod 7=5^{4} \bmod 7=625 \bmod 7=2,\) the same result.

Try it Now 6

Use the modular exponent rule to calculate \(10000 \bmod 7,\) by noting \(10000=10^{4}\)

Answer

\(10000 \bmod 7=10^{4} \bmod 7=(10 \bmod 7)^{4} \bmod 7=3^{4} \bmod 7=81 \bmod 7=4\)

This provides us the basis for our key exchange. While it will be easier to understand in the following example, here’s the process:

1. Alice and Bob agree publically on values a prime \(p\) and generator \(g\).
2. Alice picks some secret number \(a,\) while Bob picks some secret number \(b\).
3. Alice computes \(A=g^{a} \bmod p\) and sends it to Bob.
4. Bob computes \(B=g^{b}\) mod \(p\) and sends it to Alice.
5. Alice computes \(B^{a} \bmod p,\) which is \(\left(g^{b} \bmod p\right)^{a} \bmod p\).
6. Bob computes \(A^{b} \bmod p,\) which is \(\left(g^{a} \bmod p\right)^{b} \bmod p\).

The modular exponent power rule tells us \(\left(g^{a} \bmod p\right)^{b} \bmod p=\left(g^{b} \bmod p\right)^{a} \bmod p,\) so Alice and Bob will arrive at the same shared value to use as a key, even though neither knows the other's secret number, and no eavesdropper can determine this value knowing only \(g, p, A,\) and \(B\)

Example 15

Alice and Bob publically share a generator and prime modulus. In this case, we’ll use 3 as the generator and 17 as the prime.

Solution

\(\begin{array}{llll} & \textbf{Alice} & & \textbf{Bob} \\ \text{Alice and Bob publically} & g=3, p=17 & \text{Common info} & g=3, p=17 \\ \text{share a generator and prime} & & & \\ \text{modulus.} & & & \\ \text{Each then secretly picks a} & n = 8 & \text{secret number} & n=6 \\ \text{number n of their own.} & & & \\ \text{Each calculates } g^n \bmod p & 3^{8} \bmod 17=16 & & 3^{6} \bmod 17=15 \\ \text{They then exchange these} & A=16 & & B=15 \\ \text{resulting values.} & B=15 & & A=16\\ \text{Each then raises the value} & B^{n} \bmod p= & \text{mix in secret} & A^{n} \bmod p=\\ \text{they received to the power of } & & \text{number} & \\ \text{their secret }n \bmod p & 15^{8} \bmod 17=1 & & 16^{6} \bmod 17=1\\ \text{The result is the shared secret key.} & 1 & \text{shared secret key} & 1 \end{array}\)

The shared secrets come out the same because of the modular exponent power rule

\(\left(a^{b} \bmod n\right)^{c} \bmod n=\left(a^{c} \bmod n\right)^{b} \bmod n .\) Alice computed \(\left(3^{6} \bmod 17\right)^{8} \bmod 17\) while Bob computed \(\left(3^{8} \bmod 17\right)^{6} \bmod 17,\) which
the rule says will give the same results.

Notice that even if a snooper were to obtain both exchanged values \(A=16\) and \(B=15\), there is no way they could obtain the shared secret key from these without having at least one of Alice or Bob’s secret numbers. There is no easy way to obtain the secret numbers from the shared values, since the function was a one-way function.

Using this approach, Alice and Bob can now use the shared secret key obtained as the key for a standard encryption algorithm like DES or AES.

Try it Now 7

Suppose you are doing a key exchange with Kylie using generator 5 and prime 23. Your secret number is 2. What number do you send to Kylie? If Kylie sends you the value 8, determine the shared secret key.

Answer

To compute the number we'd send to Kylie, we raise the generator to the power of our secret number modulus the prime: \(5^{2} \bmod 23=25 \bmod 23=2\).

If Kylie sends us the value \(8,\) we determine the shared secret by raising her number to the power of our secret number modulus the prime: \(8^{2} \bmod 23=64 \bmod 23=18.18\) would be the shared secret.

RSA

There are several other public-key methods used, including RSA, which is very commonly used. RSA involves distributing a public encryption key, which anyone can use to encrypt messages to you, but which can only be decrypted using a separate private key. You can think of this as sending an open padlock to someone – they can lock up information, but no one can unlock it without the key you kept secret.

RSA’s security relies on the difficulty of factoring large numbers. For example, it’s easy to calculate that 53 times 59 is 3127, but given the number 12,317 that is a product of two primes, it’s much harder to find the numbers that multiply to give that number. It’s exponentially harder when the primes each have 100 or more digits. Suppose we find two primes \(p\) and \(q\) and multiply them to get \(n=p q\). This number will be very hard to factor. If we also know \(p\) and \(q\), there are shortcuts to find two numbers \(e\) and \(d\) so that \(m^{e d} \bmod n=m \bmod n\) for all numbers \(m\). Without knowing the factorization of \(n\), finding these values is very hard.

To use RSA, we generate two primes \(p\) and \(q\) and multiply them to get \(n=p q\). since we know the factorization, we can easily find \(e\) and \(d\) so \(m^{e d}=m \bmod n .\) Now, we lock away \(p\)
\(q,\) and \(d .\) We then send the values \(e\) and \(n\) out publically. To encrypt a message \(m,\) the sender computes \(S=m^{e} \bmod n .\) As we saw earlier, the modulus is a one-way function which makes the original message very hard to recover from \(S\). However, we have our private key \(d\) we can use to decrypt the message. When we receive the secret message \(S\), we compute \(S^{d} \bmod n=\left(m^{e}\right)^{d} \bmod n=m^{e d} \bmod n=m \bmod n,\) recovering the original message[4].

Example 16

Suppose that Alice has computed \(n=3127, e=3,\) and \(d=2011 .\) Show how Bob would encrypt the message 50 and how Alice would then decrypt it.

Solution

Bob would only know his message, \(m=50\) and Alice's public key: \(n=3127\) and \(e=3 .\) He would encrypt the message by computing \(m^{e} \bmod n: 50^{3} \bmod 3127=3047\)

Alice can then decrypt this message using her private key \(d\) by computing \(S^{d}\) mod \(n\):

\(3047^{2011} \bmod 3127=50\)

This method differs from Diffie-Hellman-Merkle because no exchange process is needed; Bob could send Alice an encrypted message using Bob’s public key without having to communicate with Alice beforehand to determine a shared secret key. This is especially handy for applications like encrypting email, where both parties might not be online at the same time to perform a Diffie-Hellman-Merkle style key exchange.

---

[1] en.Wikipedia.org/w/index.php?...nge.svg&page=1

[2] For a video overview of this process, see http://www.youtube.com/watch?v=YEBfamv-_do

[3] Sometime, instead of seeing 17 mod 5 = 2, you’ll see 17 ≡ 2 (mod 5). The ≡ symbol means “congruent to” and means that 17 and 2 are equivalent, after you consider the modulus 5.

[4] Many details have been left out, including how e and d are determined, and why this all works. For a bit more detail, see http://www.youtube.com/watch?v=wXB-V_Keiu8, or http://doctrina.org/How-RSA-Works-With-Examples.html