1.11: Implicit Differentiation and Rates of Change

Last updated
Save as PDF

Page ID: 25432

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Many curves of interest are not the graphs of functions. For example, for constants $a>0$ and $b>0,$ the equation

\[\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\] describes an ellipse $E$ which intersects the $x$ -axis at $(-a, 0)$ and $(a, 0)$ and the $y \text { -axis at }(-b, 0) \text { and }(b, 0) \text { (see Figure } 1.11 .1) .$ The ellipse $E$ is not the graph of a function since, for any $-a<x<a,$ both \[\left(x,-\frac{b}{a} \sqrt{a^{2}-x^{2}}\right)\] and \[\left(x, \frac{b}{a} \sqrt{a^{2}-x^{2}}\right)\] lie on $E .$ Nevertheless, we expect that $E$ will have a tangent line at every point. Note, however, that the tangent lines at $(-a, 0)$ and $(a, 0)$ are vertical lines, and so do not have a slope. At all other points, we may find the slope of the tangent line by treating $y$ in $(1.11 .1)$ as a function of $x,$ differentiating both sides of the equation with respect to $x,$ and solving for $\frac{d y}{d x} .$ In general, given a function $f$ of $x$ and $y$ and a constant $c,$ this technique will work to find the slope of the curve defined by an equation $f(x, y)=c .$ Note that in applying this technique we are assuming that $y$ is differentiable. This is in fact true for a wide range of relationships defined by $f,$ but the technical details are beyond the scope of this text.

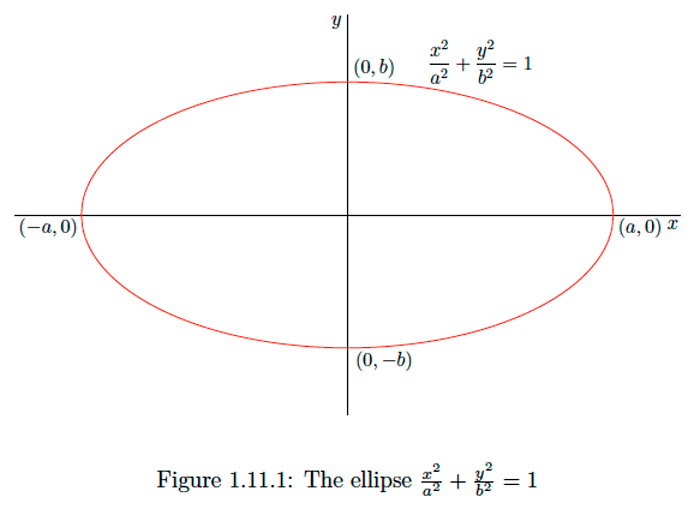
$1-11-1.png$

Example $\PageIndex{1}$

Using $a=2$ and $b=1,(1.11 .1)$ becomes, after multiplying both sides of the equation by 4,

\[x^{2}+4 y^{2}=4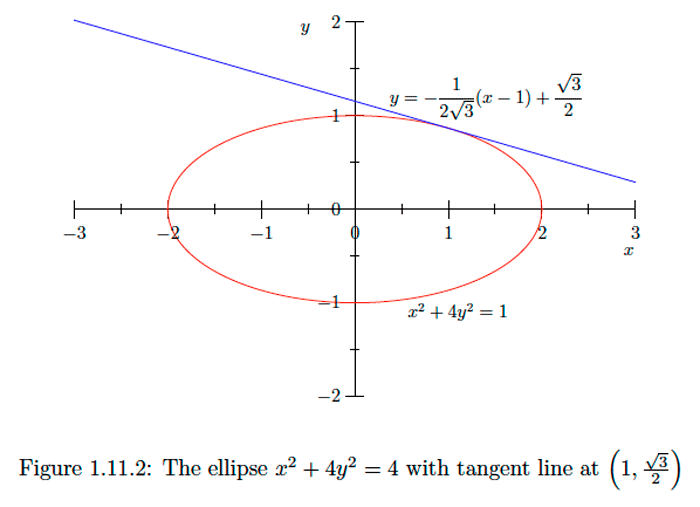 .\] Differentiating both sides of this equation by $x,$ and remembering to use the chain rule when differentiating $y^{2},$ we obtain \[2 x+8 y \frac{d y}{d x}=0 .\] Solving for $\frac{d y}{d x},$ we have \[\frac{d y}{d x}=-\frac{x}{4 y} ,\] which is defined whenever $y \neq 0$ (corresponding to the points $(-2,0)$ and $(2,0),$ at which, as we saw above, the slope of the tangent lines is undefined). For example, we have \[\left.\frac{d y}{d x}\right|_{(x, y)=\left(1, \frac{\sqrt{3}}{2}\right)}=-\frac{1}{2 \sqrt{3}} ,\] and so the equation of the line tangent to the ellipse at the point $\left(1, \frac{\sqrt{3}}{2}\right)$ is \[y=-\frac{1}{2 \sqrt{3}}(x-1)+\frac{\sqrt{3}}{2} .\] See Figure $1.11 .2 .$

$1-11-2.png$

Example $\PageIndex{2}$

Consider the hyperbola $H$ with equation

\[x^{2}-4 x y+y^{2}=4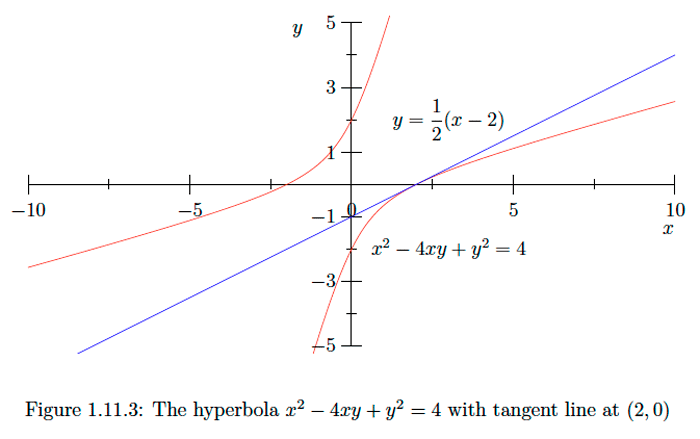 .\] Differentiating both sides of the equation, remembering to treat $y$ as a function of $x,$ we have \[2 x-4 x \frac{d y}{d x}-4 y+2 y \frac{d y}{d x}=0 .\] Solving for $\frac{d y}{d x},$ we see that \[\frac{d y}{d x}=\frac{4 y-2 x}{2 y-4 x}=\frac{2 y-x}{y-2 x} .\] For example, \[\left.\frac{d y}{d x}\right|_{(x, y)=(2,0)}=\frac{2}{4}=\frac{1}{2} .\] Hence the equation of the line tangent to $H$ at $(2,0)$ is \[y=\frac{1}{2}(x-2) .\] See Figure 1.11.3.

$1-11-3.png$

Exercise $\PageIndex{1}$

Find $\frac{d y}{d x}$ if $y^{2}+8 x y-x^{2}=10$.

Answer: $\frac{d y}{d x}=\frac{x-4 y}{4 x+y}$

Exercise $\PageIndex{2}$

Find $\left.\frac{d y}{d x}\right|_{(x, y)=(2,-1)}$ if $x^{2} y+3 x y-12 y=2$.

Answer: $\left.\frac{d y}{d x}\right|_{(x, y)=(2,-1)}=-\frac{7}{2}$

Exercise $\PageIndex{3}$

Find the equation of the line tangent to the circle with equation $x^{2}+y^{2}=25$ at the point $(3,4)$.

Answer: $y=-\frac{3}{4}(x-3)+4$

Exercise $\PageIndex{4}$

Find the equation of the line tangent to the ellipse with equation $x^{2}+x y+y^{2}=19$ at the point $(2,3)$.

Answer: $y=-\frac{7}{8}(x-2)+3$

The technique described above, known as implicit differentiation, is also useful in finding rates of change for variables related by an equation. The next examples illustrate this idea, with the first being similar to examples we saw earlier while discussing the chain rule.

Example $\PageIndex{3}$

Suppose oil is being poured onto the surface of a calm body of water. As the oil spreads out, it forms a right circular cylinder whose volume is

\[V=\pi r^{2} h ,\] where $r$ and $h$ are, respectively, the radius and height of the cylinder. Now suppose the oil is being poured out at a rate of 10 cubic centimeters per second and that the height remains a constant 0.25 centimeters. Then the volume of the cylinder is increasing at a rate of 10 cubic centimeters per second, so \[\frac{d V}{d t}=10 \mathrm{cm}^{3} / \mathrm{sec}\] at any time $t .$ Now with $h=0.25$, \[V=0.25 \pi r^{2} ,\] so \[\frac{d V}{d t}=\frac{1}{2} \pi r \frac{d r}{d t} .\] Hence \[\frac{d r}{d t}=\frac{2}{\pi r} \frac{d V}{d t}=\frac{20}{\pi r} \mathrm{cm} / \mathrm{sec} .\] For example, if $r=10$ centimeters at some time $t=t_{0},$ then \[\left.\frac{d r}{d t}\right|_{t=t_{0}}=\frac{20}{10 \pi}=\frac{2}{\pi} \approx 0.6366 \mathrm{cm} / \mathrm{sec} .\]

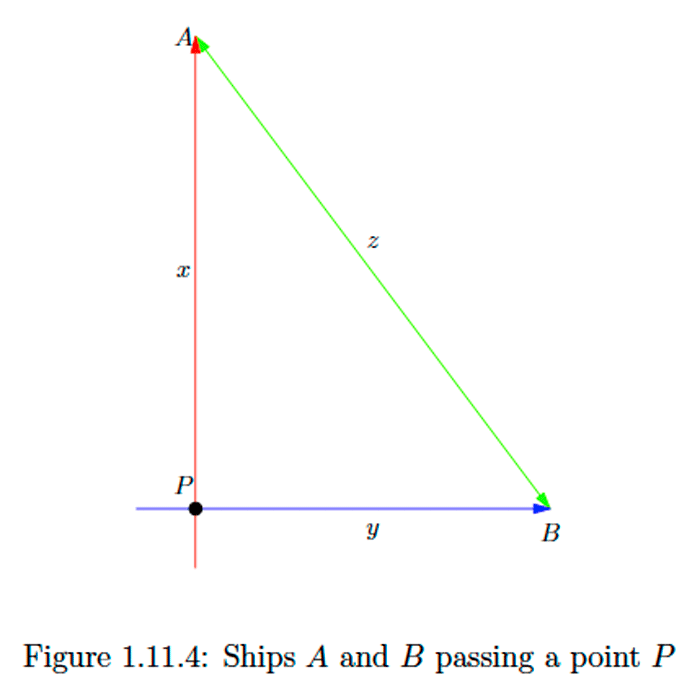
$1-11-4.png$

Example $\PageIndex{4}$

Suppose ship $A,$ headed due north at 20 miles per hour, and ship $B,$ headed due east at 30 miles per hour, both pass through the same point $P$ in the ocean, ship $A$ at noon and ship $B$ two hours later (see Figure 1.11.4) If we let $x$ denote the distance from $A$ to $P$ $t$ hours after noon, $y$ denote the

distance from $B$ to $P$ $t$ hours after noon, and $z$ denote the distance from $A$ to $B$ $t$ hours after noon, then, by the Pythagorean theorem, \[z^{2}=x^{2}+y^{2} .\] Differentiating this equation with respect to $t$, we find \[2 z \frac{d z}{d t}=2 x \frac{d x}{d t}+2 y \frac{d y}{d t} ,\] or \[z \frac{d z}{d t}=x \frac{d x}{d t}+y \frac{d y}{d t} .\] For example, at 4 in the afternoon, that is, when $t=4,$ we know that \[\begin{array}{l}{x=(4)(20)=80 \text { miles, }} \\[12pt] {y=(2)(30)=60 \text { miles, }}\end{array}\] and \[z=\sqrt{80^{2}+60^{2}}=100 \text { miles, }\] so \[100 \frac{d z}{d t}=80 \frac{d x}{d t}+60 \frac{d y}{d t} \text { miles / hour. } \] Since at any time $t$, \[\frac{d x}{d t}=20 \text { miles } / \text { hour }\] and \[\frac{d y}{d t}=30 \text { miles /hour, }\] we have \[\left.\frac{d z}{d t}\right|_{t=4}=\frac{(80)(20)+(60)(30)}{100}=34 \text { miles /hour. }\]

Exercise $\PageIndex{5}$

Suppose the volume of a cube is growing at a rate of 150 cubic centimeters per second. Find the rate at which the length of a side of the cube is growing when each side of the cube is 10 centimeters.

Answer: $\frac{1}{2} \mathrm{cm} / \mathrm{sec}$

Exercise $\PageIndex{6}$

A plane flies over a point $P$ on the surface of the earth at a height of 4 miles. Find the rate of change of the distance between $P$ and the plane one minute later if the plane is traveling at 300 miles per hour.

Answer: 234.26 miles $/$ hour

Exercise $\PageIndex{7}$

Suppose the length of a rectangle is growing at a rate of 2 centimeters per second and its width is growing at a rate of 4 centimeters per second. Find the rate of change of the area of the rectangle when the length is 10 centimeters and the width is 12 centimeters.

Answer: $64 \mathrm{cm}^{2} / \mathrm{sec}$