1.8: Geometry of Numbers

We have already seen that geometrical concepts are sometimes useful in illuminating number theoretic considerations. With the introduction by Minkowski of geometry of numbers a real welding of important parts of number theory and geometry was achieved. This branch of mathematics has been in considerable vogue in the last 20 years, particularly in England where it was and is being developed vigorously by Mordell, Davenport, Mahler and their students.

We shall consider a very brief introduction to this subject. First, we shall examine a proof of the fundamental theorem of Minkowski due to Hajos (1934), then we shall discuss some generalizations and applications of this theorem, and finally we shall investigate some new results and conjectures that are closely related.

In its simplest form the fundamental theorem of Minkowski is the following.

Theorem $\PageIndex{1}$: Fundamental Theorem of Minkowski

Let $R$ be a region in the $x-y$ plane of area $A > 4$, symmetric about the origin and convex. Then $R$ contains a lattice point other than the origin.

First, some preliminary remarks. In the condition $A > 4$, the 4 cannot be replaced by any smaller number. This may be seen by considering the square of side $2 − \epsilon$, centered at the origin. Indeed this example might at first suggest that the theorem is quite intuitive, as it might seem that squeezing this region in any direction and keeping its area fixed would necessarily force the region to cover some lattice point. However the matter is not quite so simple, as other examples reveal that neither central symmetry nor convexity are indispensable. As far as convexity is concerned what is really needed is that with the vectors $\vec{V_1}$ and $\vec{V_2}$ the region should also contain $\dfrac{1}{2} (\vec{V_1} + \vec{V_2})$. The symmetry means that with $\vec{V_1}$ the vector $-\vec{V_1}$ should also be in $R$. Thus the symmetry and convexity together imply that, if $\vec{V_1}$ and $\vec{V_2}$ are in $R$, so is $\dfrac{1}{2} (\vec{V_1} - \vec{V_2})$. This last condition is really sufficient for our purpose and may replace the conditions of symmetry and convexity. It is implied by symmetry and convexity but does not imply either of these conditions.

Another example that perhaps illuminates the significance of Minkowski’s theorem is the following. Consider a line through $O$ having irrational slope $\tan \theta$; see Figure 4. This line passes through no lattice point other than the origin. If we take a long segment of this line, say extending length $R$ on either side of $O$, then there will be a lattice point closest to, and a distance $r$ from,

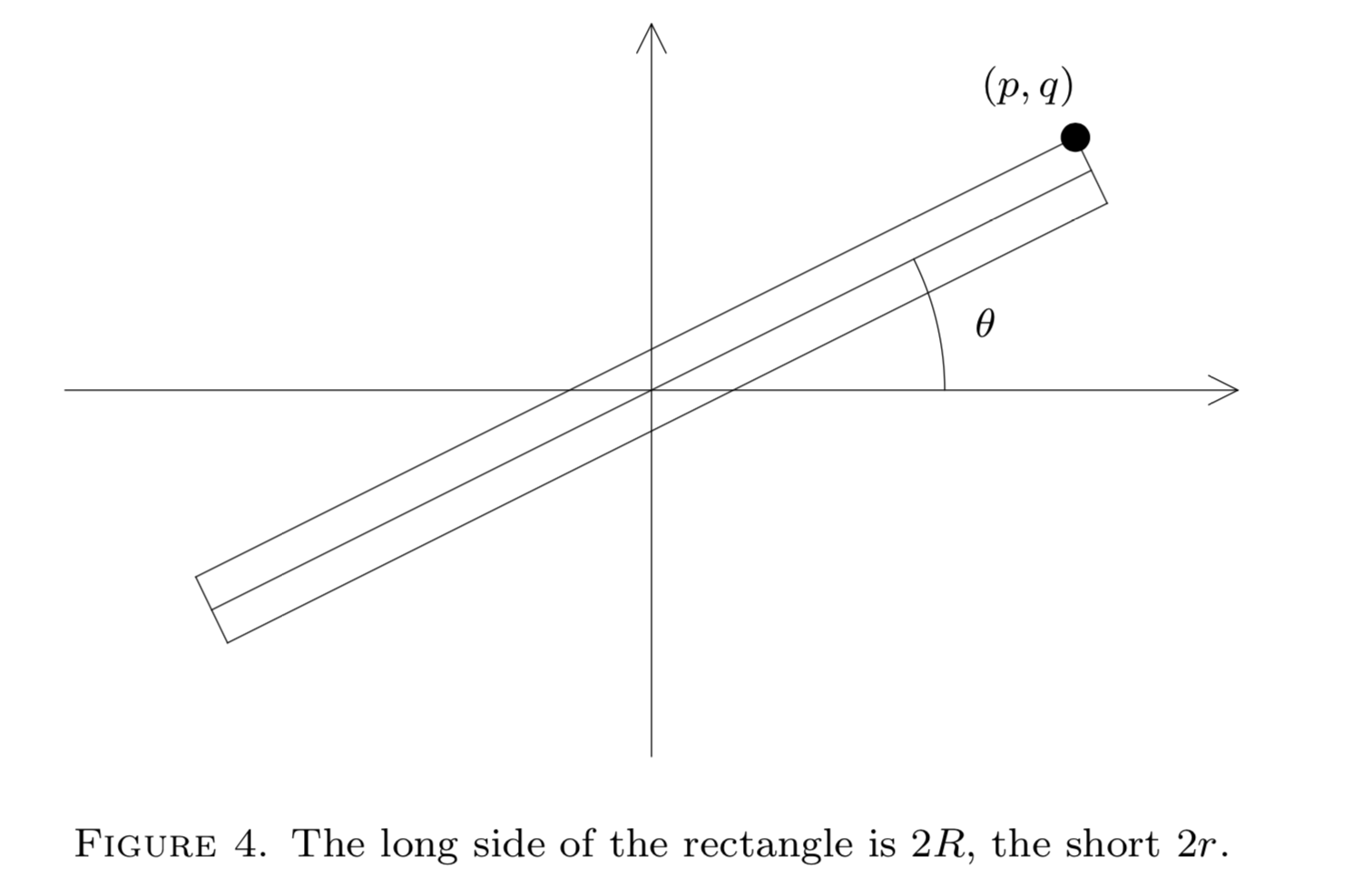
this segment. Hence, no matter how large $R$ is, we can construct a rectangle containing this line segment, which contains no lattice point other than $O$. By the fundamental theorem of Minkowski the area $4rR$ of this rectangle does not exceed 4. Thus $r \le \dfrac{1}{R}$. Note that if $(p, q)$ is a lattice point on the border of the rectangle then $\dfrac{p}{q} \approx \tan \theta$, so that the fundamental theorem of Minkowski will give some information about how closely an irrational number can be approximated by rationals.

Let us now return to Hajos proof of the fundamental theorem of Minkowski. Consider the $x-y$ plane cut up into an infinite chessboard with the basic square of area 4 determined by $|x| \le 1$, $|y| \le 1$. We now cut up the chessboard along the edges of the squares and superimpose all the squares that contain parts of the region $R$. We have now compressed an area > 4 into a region of area 4. This implies that there will be some overlapping, i.e., one can stick a pin through the square so as to pierce $R$ into two points say $V_1$ and $V_2$. Now reassemble the region and let the points $V_1$ and $V_2$ be the vectors $\vec{V_1}$ and $\vec{V_2}$. Consider the fact that the $x$ and $y$ coordinates of $V_1$ and $V_2$ differ by a multiple of 2. We write $V_1 \equiv V_2$ (mod 2), which implies $\dfrac{1}{2} (V_1 - V2) \equiv 0$ (mod 1). Thus $\dfrac{1}{2} (V_1 - V_2)$ is a lattice point different from O (since $V_1 \ne V_2$) in $R$.

The fundamental theorem of Minkowski can easily be generalized to $n$-dimensional space. Indeed we need only replace 4 in the fundamental theorem of Minkowski by 2n and Hajos’ proof goes through. Many extensions and re- finements of the fundamental theorem of Minkowski have been given. I shall return to some of them later.

One of Polya’s earliest papers has the long and curious title “Zahlhlentheoretisches und Wahrscheinlichkeitstheoretisches $\ddot{u}$ber die Sichtweite in Walde und durch Schneefall”. A proof of Polya’s main result in this paper can be greatly simplified and somewhat refined using the fundamental theorem of Minkowski. The problem is this.

Suppose every lattice point other than $O$ is surrounded by a circle of radius $r \le \dfrac{1}{2}$ (a tree in a forest). A man stands at $O$. In direction $\theta$ he can see a distance $f(r, \theta)$. distance f(r,θ). What is the furthest he can see in any direction? That is, determine

$F(r) = \text{max}_{\theta} f(\theta, r)$

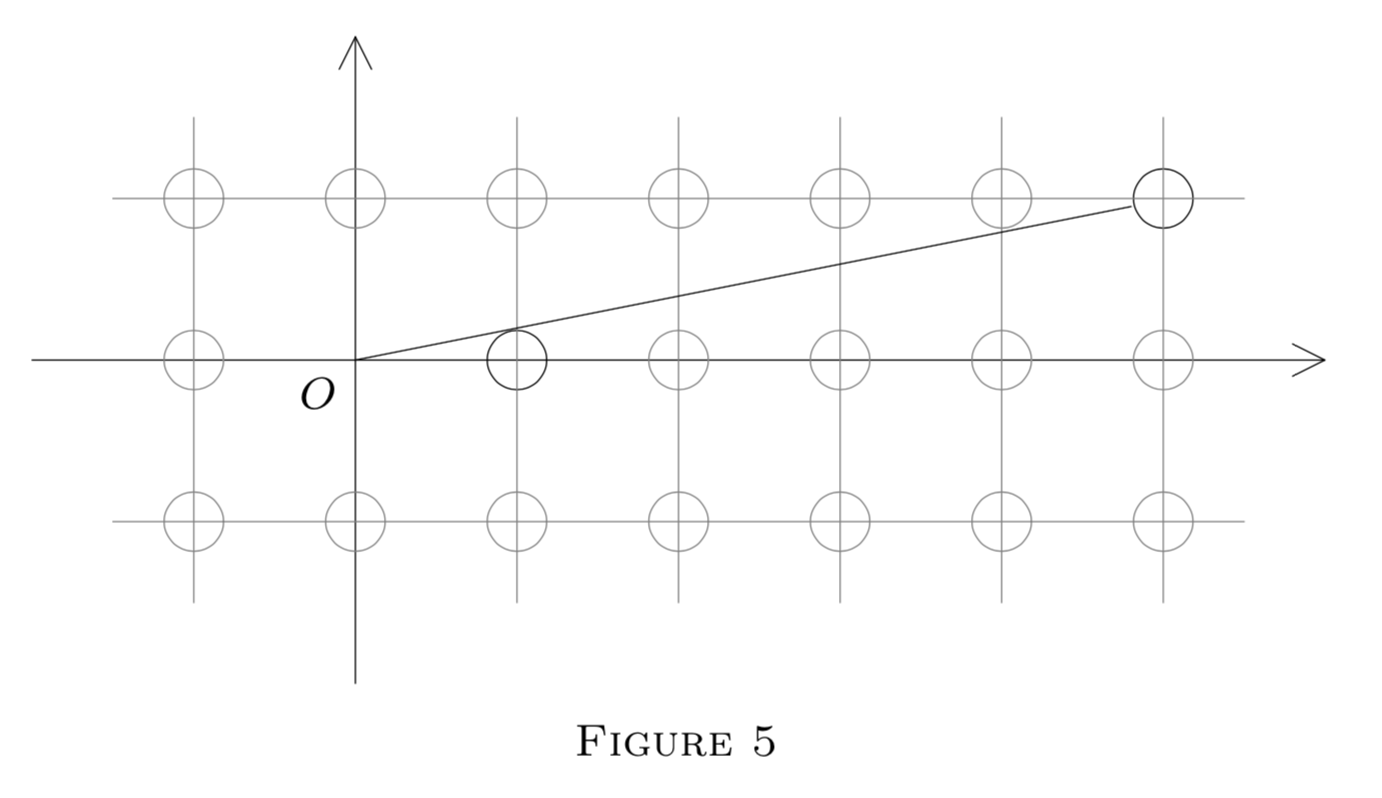
By looking past the circle centered at (1, 0) (Figure 5), we can see almost a distance $\dfrac{1}{r}$. On the other hand we can prove that $F(r) \le \dfrac{1}{r}$. For suppose that we can see a distance $F(r)$ in direction θ. About this line of vision construct a rectangle with side $2r$. This rectangle contains no lattice point, for otherwise the tree centered at such a lattice point would obstruct our line of vision; see Figure 6.

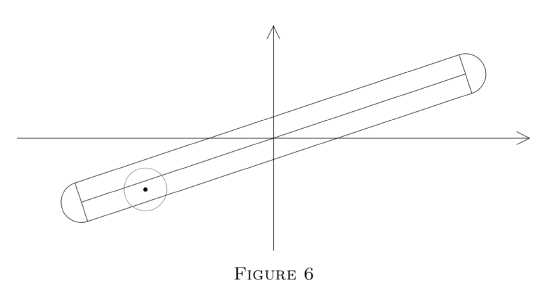
Hence, by the fundamental theorem of Minkowski $4F(r) r \le 4$ and $F(r) \le \dfrac{1}{r}$ as required. Note that no lattice point can be in either semicircle in the diagram. This enables us to improve slightly on Polya’s result. I shall leave the details as an exercise.

A more significant application of the fundamental theorem of Minkowski concerns the possibility of solving in integers a set of linear inequalities.

Consider the inequalities

$|a_{11} x_{1} + a_{12}x_{2} + \cdot\cdot\cdot + a_{1n}x_{n}| \le \lambda_1,$
$|a_{21} x_{1} + a_{22}x_{2} + \cdot\cdot\cdot + a_{2n}x_{n}| \le \lambda_2,$
.
.
.
$|a_{n1} x_{1} + a_{n2}x_{2} + \cdot\cdot\cdot + a_{nn}x_{n}| \le \lambda_n,$

where the $a_{ij}$ are real numbers and the $\lambda_1, \lambda_2, ..., \lambda_n$ are positive numbers. The problem is to find sufficient conditions for the existence of integers $x_1, ..., x_n$, not all 0 satisfying the system. The fundamental theorem of Minkowski can be used to prove that a solution will exist provided the determinant det(aij) of the coefficients is, in absolute value, less than the product $\lambda_1 \cdot \lambda_2 \cdot\cdot\cdot\cdot\cdot \lambda_n$. This comes about in the following way. Geometrically, the inequalities determine an $n$−dimensional parallelepiped whose volume (or content) is

$\dfrac{1}{\text{det} (a_{ij})} \cdot 2^n \cdot \lambda_1 \cdot \lambda_2 \cdot\cdot\cdot\cdot\cdot \lambda_n.$

If $\lambda_1 \cdot \lambda_2 \cdot\cdot\cdot\cdot\cdot \lambda_n > \text{det} (a_{ij})$ then the content exceeds $2^n$ and so contains a lattice point different from $O$.

A very recent analogue of the fundamental theorem of Minkowski is the following. Let $R$ be a convex region, not necessarily symmetric about O, but having its centroid at $O$. If its area exceeds $\dfrac{9}{2}$, then it contains a lattice point not $O$. The constant $\dfrac{9}{2}$ is again best possible, but an n-dimensional analogue of this result is unknown.

The following is a conjectured generalization of the fundamental theorem of Minkowski, which we have unfortunately been unable to prove. Perhaps you will be able to prove or disprove it. Let $R$ be a convex region containing the origin and defined by $r = f(\theta)$, $0 \le \theta < 2 \pi$. If

$\int_0^{\pi} f(\theta) f(\theta + \pi) d \theta > 4$

then $R$ contains a nontrivial lattice point. For symmetrical regions $f(\theta) = f(\theta + \pi)$, and the conjecture reduces to the fundamental theorem of Minkowski.

Here is a somewhat related and only partially solved problem. Let $M(n)$ be defined as the smallest number such that any convex region of area $M(n)$ can be placed so as to cover $n$ lattice points. Clearly $M(1) = 0$. It is not difficult to show that $M(2) = \dfrac{\pi}{4}$, i.e., any convex region whose area exceeds that of a circle of diameter 1 can be used to cover 2 lattice points. To determine $M(3)$ already seems difficult. What one can easily prove is that $M(n) \le n -1$ and we conjecture the existence of a positive constant $c$ such that $M(n) < n - c \sqrt{n}$.