5.4: Reflection across a line
( \newcommand{\kernel}{\mathrm{null}\,}\)
Assume the point
According to Theorem 5.3.1,
Note that
Assume
- Proof
-
Note that if
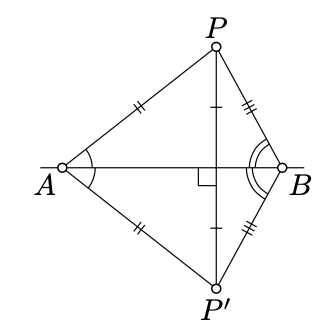
If
Since
The reflection across a line is a motion of the plane. Moreover, if
- Proof
-
Note that the composition of two reflections across the same line is the identity map. In particular, any reflection is a bijection.
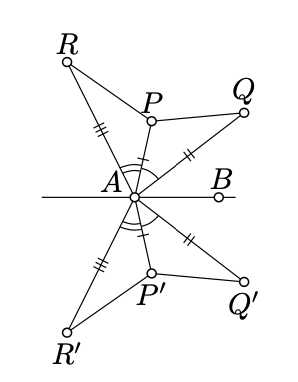
Fix a line
that is, the reflection is distance-preserving, Without loss of generality, we may assume that the points
It follows that
By SAS,
From 5.4.2 and the theorem on the signs of angles of triangles (Theorem 3.3.1) we get
Repeating the same argument for a pair of points
Subtracting 5.4.4 from 5.4.3, we get that
Show that any motion of the plane can be presented as a composition of at most three reflections across lines.
- Hint
-
Choose an arbitrary nondegenerate triangle
If
If
Finally, if
Apply Exercise 4.4.3 to show that the composition of the constructed reflections coincides with the given motion.
The motions of plan can be divided into two types, direct and indirect. The motion
for any
for any
Indeed, by Corollary
Let
- Answer
-
Note that


