10.5: Perpendicular circles
- Page ID
- 23644
Assume two circles \(\Gamma\) and \(\Omega\) intersect at two points \(X\) and \(Y\). Let \(\ell\) and \(m\) be the tangent lines at \(X\) to \(\Gamma\) and \(\Omega\) respectively. Analogously, \(\ell'\) and \(m'\) be the tangent lines at \(Y\) to \(\Gamma\) and \(\Omega\).
From Exercise 9.6.3, we get that \(\ell \perp m\) if and only if \(\ell' \perp m'\).
We say that the circle \(\Gamma\) is perpendicular to the circle \(\Omega\) (briefly \(\Gamma \perp \Omega\)) if they intersect and the lines tangent to the circles at one point (and therefore, both points) of intersection are perpendicular.
Similarly, we say that the circle \(\Gamma\) is perpendicular to the line \(\ell\) (briefly \(\Gamma \perp \ell\)) if \(\Gamma \cap \ell \ne \emptyset\) and \(\ell\) perpendicular to the tangent lines to \(\Gamma\) at one point (and therefore, both points) of intersection. According to Lemma 5.6.2, it happens only if the line l passes thru the center of \(\Gamma\).
Now we can talk about perpendicular circlines.
Assume \(\Gamma\) and \(Omega\) are distinct circles. Then \(\Omega \perp \Gamma\) if and only if the circle \(\Gamma\) coincides with its inversion in \(\Omega\).
- Proof
-
Suppose that \(\Gamma'\) denotes the inverse of \(\Gamma\).
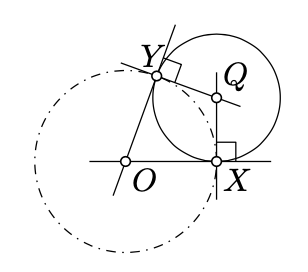
"Only if" part. Let \(O\) be the center of \(\Omega\) and \(Q\) be the center of \(\Gamma\). Let \(X\) and \(Y\) denote the points of intersections of \(\Gamma\) and \(Omega\). According to Lemma 5.6.2, \(\Omega \perp \Gamma\) if and only if \((OX)\) and \((OY)\) are tangent to \(\Gamma\).
Note that \(\Gamma'\) is also tangent to \((OX)\) and \((OY)\) and \(X\) and \(Y\) respectively. It follows that \(X\) and \(Y\) are the foot points of the center of \(\Gamma'\) on \((OX)\) and \((OY)\). Therefore, both \(\Gamma'\) and \(\Gamma\) have the center \(Q\). Finally, \(\Gamma' = \Gamma\), since both circles pass thru \(X\).
"If" part. Assume \(\Gamma = \Gamma'\).
Since \(\Gamma \ne \Omega\), there is a point \(P\) that lies on \(\Gamma\), but not on \(\Omega\). Let \(P'\) be the inverse of \(P\) in \(\Omega\). Since \(\Gamma = \Gamma'\), we have that \(P' \in \Gamma\). In particular, the half-line \([OP)\) intersects \(\Gamma\) at two points. By Exercise 5.6.1, \(O\) lies outside of \(\Gamma\).
As \(\Gamma\) has points inside and outside of \(\Omega\), the circles \(\Gamma\) and \(\Omega\) intersect. The latter follows from Exercise 3.5.1.
Let \(X\) be point of their intersection. We need to show that \((OX)\) is tangent to \(\Gamma\); that is, \(X\) is the only intersection point of \((OX)\) and \(\Gamma\).
Assume \(Z\) is another point of intersection. Since \(O\) is outside of \(\Gamma\), the point \(Z\) lies on the half-line \([OX)\).
Suppose that \(Z'\) denotes the inverse of \(Z\) in \(\Omega\). Clearly, the three points \(Z\), \(Z'\), \(X\) lie on \(\Gamma\) and \((OX)\). The latter contradicts Lemma 5.6.1.
It is convenient to define the inversion in the line \(\ell\) as the reflection across \(\ell\). This way we can talk about inversion in an arbitrary circline.
Let \(\Omega\) and \(\Gamma\) be distinct circlines in the inversive plane. Then the inversion in \(\Omega\) sends \(\Gamma\) to itself if and only if \(\Omega \perp \Gamma\).
- Proof
-
By Thorem \(\PageIndex{1}\), it is sufficient to consider the case when \(\Omega\) or \(\Gamma\) is a line.
Assume \(\Omega\) is a line, so the inversion in \(\Omega\) is a reflection. In this case the statement follows from Corollary 5.4.1.
If \(\Gamma\) is a line, then the statement follows from Theorem 10.3.2.
Let \(P\) and \(P'\) be two distinct points such that \(P'\) is the inverse of \(P\) in the circle \(\Omega\). Assume that the circline \(\Gamma\) passes thru \(P\) and \(P'\). Then \(\Gamma \perp \Omega\).
- Proof
-
Without loss of generality, we may assume that \(P\) is inside and \(P'\) is outside \(\Omega\). By Theorem 3.5.1, \(\Gamma\) intersects \(\Omega\). Suppose that A denotes a point of intersection.
Suppose that \(\Gamma'\) denotes the inverse of \(\Gamma\). Since \(A\) is a self-inverse, the points \(A, P\), and \(P'\) lie on \(\Gamma'\). By Exercise 8.1.1, \(\Gamma'\) = \(\Gamma\) and by Theorem \(\PageIndex{1}\), \(\Gamma \perp \Omega\).
Let \(P\) and \(Q\) be two distinct points inside the circle \(\Omega\). Then there is a unique circline \(\Gamma\) perpendicular to \(\Omega\) that passes thru \(P\) and \(Q\).
- Proof
-
Let \(P'\) be the inverse of the point \(P\) in the circle \(\Omega\). According to Corollary \(\PageIndex{2}\), the circline is passing thru \(P\) and \(Q\) is perpendicular to \(\Omega\) if and only if it passes thru \(P'\).
Note that \(P'\) lies outside of \(\Omega\). Therefore, the points \(P\), \(P'\), and \(Q\) are distinct.
According to Exercise Exercise 8.1.1, there is a unique circline passing thru \(P, Q\), and \(P'\). Hence the result.
Let \(P, Q, P'\), and \(Q'\) be points in the Euclidean plane. Assume \(P'\) and \(Q'\) are inverses of \(P\) and \(Q\) respectively. Show that the quadrangle \(PQP'Q'\) is inscribed.
- Hint
-
Apply Theorem 10.2.1, Theorem 7.4.5 and Theorem 9.2.1.
Let \(\Omega_1\) and \(\Omega_2\) be two perpendicular circles with centers at \(O_1\) and \(O_2\) respectively. Show that the inverse of \(O_1\) in \(\Omega_2\) coincides with the inverse of \(O_2\) in \(\Omega_1\).
- Hint
-
Suppose that \(T\) denotes a point of intersection of \(\Omega_1\) and \(\Omega_2\). Let \(P\) be the foot point of \(T\) on \((O_1O_2)\). Show that \(\triangle O_1PT \sim \triangle O_1TO_2 \sim \triangle TPO_2\). Consider that \(P\) coincides with the inverses of \(O_1\) in \(\Omega_2\) and of \(O_2\) in \(\Omega_1\).
Three distinct circles — \(\Omega_1\), \(\Omega_2\) and \(\Omega_3\), intersect at two points — \(A\) and \(B\). Assume that a circle \(\Gamma\) is perpendicular to \(\Omega_1\) and \(\Omega_2\). Show that \(\Gamma \perp \Omega_3\).
- Hint
-
Since \(\Gamma \perp \Omega_1\) and \(\Gamma \perp \Omega_2\), Corollary \(PageIndex{1}\) implies that the circles \(\Omega_1\) and \(\Omega_2\) are inverted in \(\Gamma\) to themselves. Conclude that the points \(A\) and \(B\) are inverse of each other. Since \(\Omega_3 \ni A, B\), Corollary \(\PageIndex{2}\) implies that \(\Omega_3 \perp \Gamma\).
Let us consider two new construction tools: the circumtool that constructs a circline thru three given points, and the inversion-tool — a tool that constructs an inverse of a given point in a given circline.
Given two circles \(\Omega_1\), \(\Omega_2\) and a point \(P\) that does not lie on the circles, use only circum-tool and inversion-tool to construct a circline \(\Gamma\) that passes thru \(P\), and perpendicular to both \(\Omega_1\) and \(\Omega_2\).
- Hint
-
Let \(P_1\) and \(P_2\) be the inverse of \(P\) in \(\Omega_1\) and \(\Omega_2\). Apply Corollary \(\PageIndex{2}\) and Theorem \(\PageIndex{1}\) to show that a circline \(\Gamma\) that pass thru
\(P, P_1\), and \(P_3\) is a solution.
Given three disjoint circles \(\Omega_1\), \(\Omega_2\) and \(\Omega_3\), use only circum-tool and inversion-tool to construct a circline \(\Gamma\) that perpendicular to each circle \(\Omega_1\), \(\Omega_2\) and \(\Omega_3\).
Think what to do if two of the circles intersect.
- Hint
-
All circles that perpendicular to \(\Omega_1\) and \(\Omega_2\) pass thru a fixed point \(P\). Try to construct \(P\).
If two of the circles intersect, try to apply Corollary 10.6.1.