11.3: Three angles of triangle

Proposition $\PageIndex{1}$

Let $\triangle ABC$ and $\triangle A'B'C'$ be two triangles in the neutral plane such that $AC = A'C'$ and $BC = B'C'$. Then

$AB < A'B'$ if and only if $|\measuredangle ACB| < |\measuredangle A'C'B'|$.

Proof

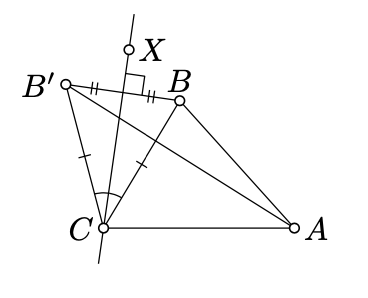
Without loss of generality, we may assume that $A = A'$, $C = C'$, and $\measuredangle ACB$, $\measuredangle ACB' \ge 0$. In this case we need to show that

$AB < AB' \Leftrightarrow \measuredangle ACB < \measuredangle ACB'.$

Choose a point $X$ so that

$\measuredangle ACX = \dfrac{1}{2} \cdot (\measuredangle ACB + \measuredangle ACB').$

Note that

• $(CX)$ bisects $\angle BCB'$.
• $(CX)$ is the perpendicular bisector of $[BB']$.
• $A$ and $B$ lie on the same side of $(CX)$ if and only if

$\measuredangle ACB < \measuredangle ACB'$.

From Exercise 5.2.1, $A$ and $B$ lie on the same side of $(CX)$ if and only if $AB < AB'$. Hence the result.

Theorem $\PageIndex{1}$

Let $\triangle ABC$ be a triangle in the neutral plane. Then

$|\measuredangle ABC| + |\measuredangle BCA| + |\measuredangle CAB| \le \pi.$

The following proof is due to Legendre [12], earler proofs were due to Saccheri [16] and Lambert [11].

Proof

Set

$\begin{array} {rclcrclcrcl} {a} & = & {BC,} & \ \ \ \ \ & {b} & = & {CA,} & \ \ \ \ \ & {c} & = & {AB,} \\ {\alpha} & = & {\measuredangle CAB,} & \ \ \ \ \ & {\beta} & = & {\measuredangle ABC,} & \ \ \ \ \ & {\gamma} & = & {\measuredangle BCA.} \end{array}$

Without loss of generality, we may assume that $\alpha, \beta, \gamma \ge 0$.

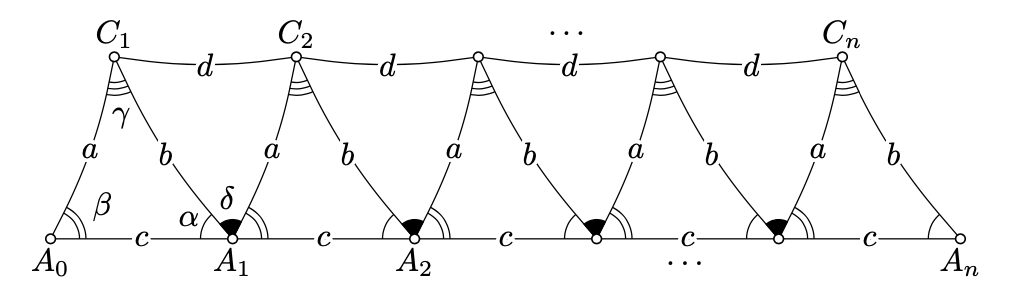
Fix a positive integer $n$. Consider the points $A_0, A_1, ..., A_n$ on the half-line $[BA)$, such that $BA_i = i \cdot c$ for each $i$. (In particular, $A_0 = B$ and $A_1 = A$.) Let us construct the points $C_1, C_2, ..., C_n$, so that $\measuredangle A_iA_{i-1}C_i = \beta$ and $A_{i-1} C_i = a$ for each $i$.

By SAS, we have constructed n congruent triangles

$\triangle ABC = \triangle A_1A_0C_1 \cong \triangle A_2A_1C_2 \cong ... \cong \triangle A_nA_{n-1} C_n.$

Set $d = C_1C_2$ and $\delta = \measuredangle C_2A_1C_1$. Note that

$$\alpha + \beta + \delta = \pi.$$

By Proposition 11.2.1, we get that $\Delta \ge 0$.

By construction

$\triangle A_1C_1C_2 \cong \triangle A_2C_2C_3 \cong ... \cong \triangle A_{n - 1} C_{n - 1} C_n.$

In particular, $C_i C_{i + 1} = d$ for each $i$.

By repeated application of the triangle inequality, we get that

$\begin{array} {rcl} {n \cdot c} & = & {A_0A_n \le} \\ {} & \le & {A_0 C_1 + C_1 C_2 + \cdots + C_{n - 1} C_n + C_n A_n =} \\ {} & = & {a + (n - 1) \cdot d + b.} \end{array}$

In particular,

$c \le d + \dfrac{1}{n} \cdot (a + b - d).$

Since $n$ is arbitrary positive integer, the latter implies $c \le d$. By Proposition $\PageIndex{1}$, it is equivalent to

$\gamma \le \delta.$

From 11.3.1, the theorem follows.

Exercise $\PageIndex{1}$

Let $ABCD$ be a quadrangle in the neutral plane. Suppose that the angles $DAB$ and $ABC$ are right. Show that $AB \le CD$.

Hint

Set $a = AB, b = BC, c = CD$, and $d = DA$; we nned to show that $c \ge a$.

Mimic the proof of Theorem $\PageIndex{1}$ for the shown fence made from copies of quadrangle $ABCD$.