1.5: Triangles
- Page ID
- 34121
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A triangle is formed when three straight line segments bound a portion of the plane. The line segments are called the sides of the triangle. A point where two sides meet is called a vertex of the triangle, and the angle formed is called an angle of the triangle. The symbol for triangle is \(\triangle\).
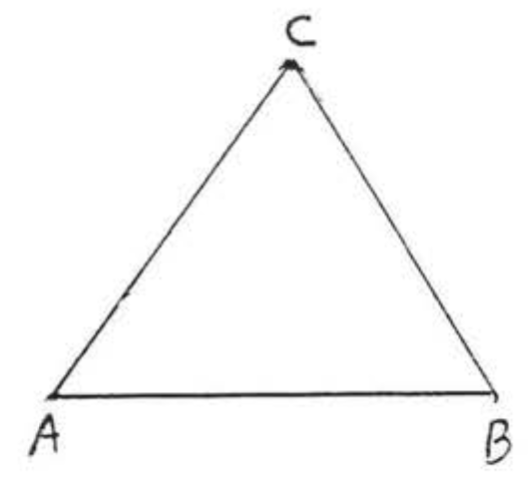
The triangle in Figure \(\PageIndex{1}\) is denoted by \(\triangle ABC\) (or \(\triangle BCA\) or \(\triangle CAB\), etc.).
- Its sides are \(AB\), \(AC\), and \(BC\).
- Its vertices are \(A, B\), and \(C\).
- Its angles are \(\angle A\), \(\angle B\), and \(\angle C\).
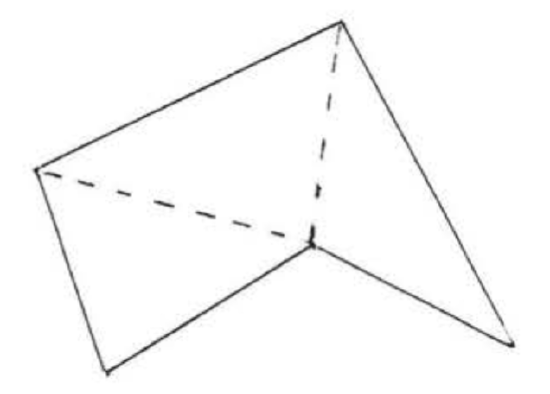
The triangle is the most important figure in plane geometry, This is because figures with more than three sides can always be divided into triangles (Figure \(\PageIndex{2}\)). If we know the properties of a triangle, we can extend this knowledge to the study of other figures as well.
A fundamental property of triangles is the following:
The sum of the angles of a triangle is \(180^{\circ}\).
In \(\triangle ABC\) of Figure \(\PageIndex{1}\), \(\angle A + \angle B + \angle C = 180^{\circ}\).
Find \(\angle C\):
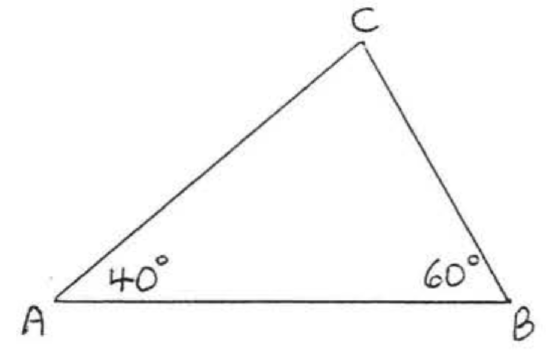
Solution
\[\begin{array} {rcl} {\angle A + \angle B + \angle C} & = & {180^{\circ}} \\ {40^{\circ} + 60^{\circ} + \angle C} & = & {180^{\circ}} \\ {100^{\circ} + \angle C} & = & {180^{\circ}} \\ {\angle C} & = & {180^{\circ} - 100^{\circ}} \\ {\angle C} & = & {80^{\circ}} \end{array} \nonumber\]
Answer: \(\angle C = 80^{\circ}\)
Proof of Theorem \(\PageIndex{1}\): Through \(C\) draw \(DE\) parallel to \(AB\) (see Figure \(\PageIndex{3}\)). Note that we are using the parallel postulate here, \(\angle 1 = \angle A\) and \(\angle 3 = \angle B\) because they are alternate interior angles of parallel lines, Therefore \(\angle A + \angle B + \angle C = \angle 1 + \angle 3 + \angle 2 = 180^{\circ}\).
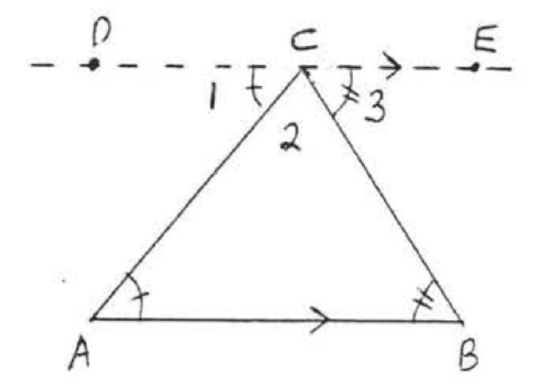
We may verify Theorem \(\PageIndex{1}\) by measuring the angles of a triangle with a protractor and taking the sum, However no measuring instrument is perfectly accurate, It is reasonable to expect an answer such as \(179^{\circ}\), \(182^{\circ}\), \(180.5^{\circ}\), etc. The purpose of our mathematical proof is to assure us that the sum of the angles of every triangle must be exactly \(180^{\circ}\).
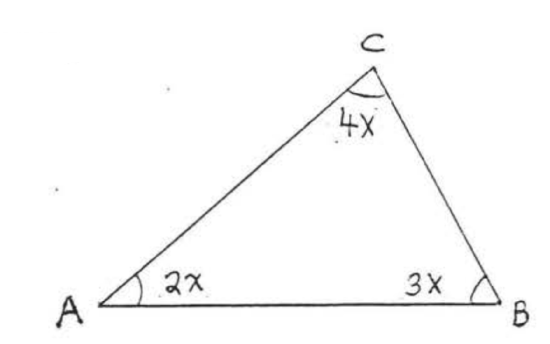
Find \(x\):
Solution
\[\begin{array} {rcl} {\angle A + \angle B + \angle C} & = & {180^{\circ}} \\ {2x + 3x + 4x} & = & {180} \\ {9x} & = & {180} \\ {x} & = & {20} \end{array} \nonumber\]
Check:
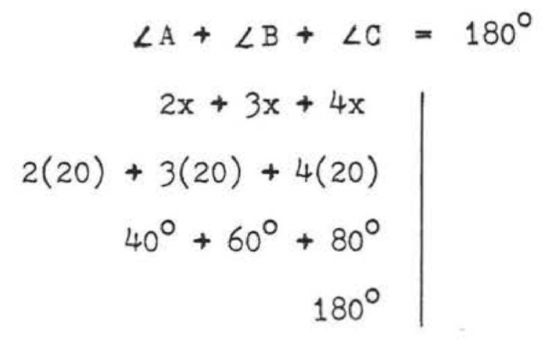
Answer: \(x = 20\).
Find \(y\) and \(x\):
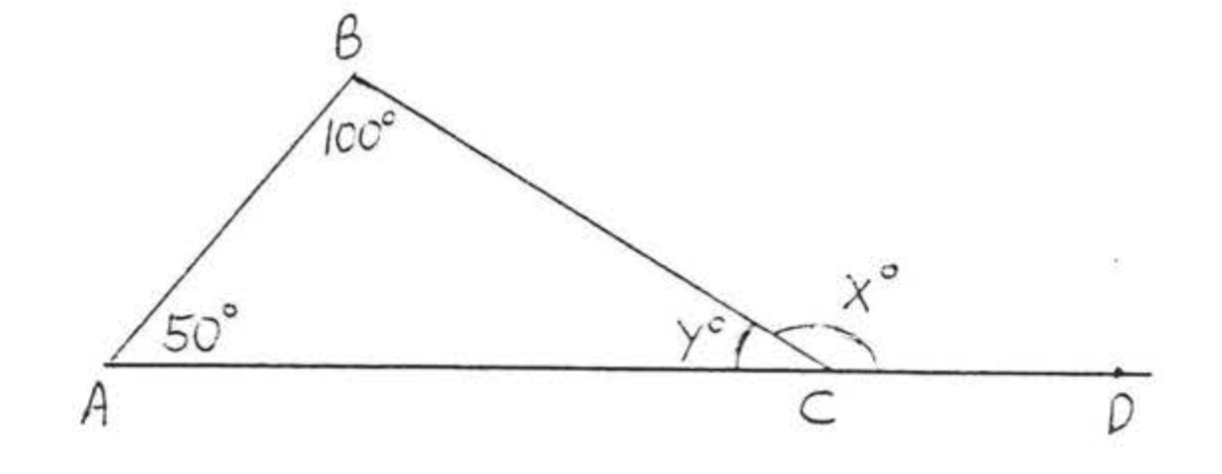
Solution
\[\begin{array} {rcl} {50 + 100 + y} & = & {180} \\ {150 + y} & = & {180} \\ {y} & = & {180 - 150} \\ {y} & = & {30} \\ {} & & {} \\ {x} & = & {180 - 30 = 150} \end{array}\]
Answer: \(y = 30\), \(x = 150\).
In Figure \(\PageIndex{4}\), \(\angle x\) is called an exterior angle of \(\triangle ABC\), \(\angle A\), \(\angle B\), and \(\angle y\) are called the interior angles of \(\triangle ABC\). \(\angle A\) and \(\angle B\) are said to be the interior angles remote from the exterior angle \(\angle x\).
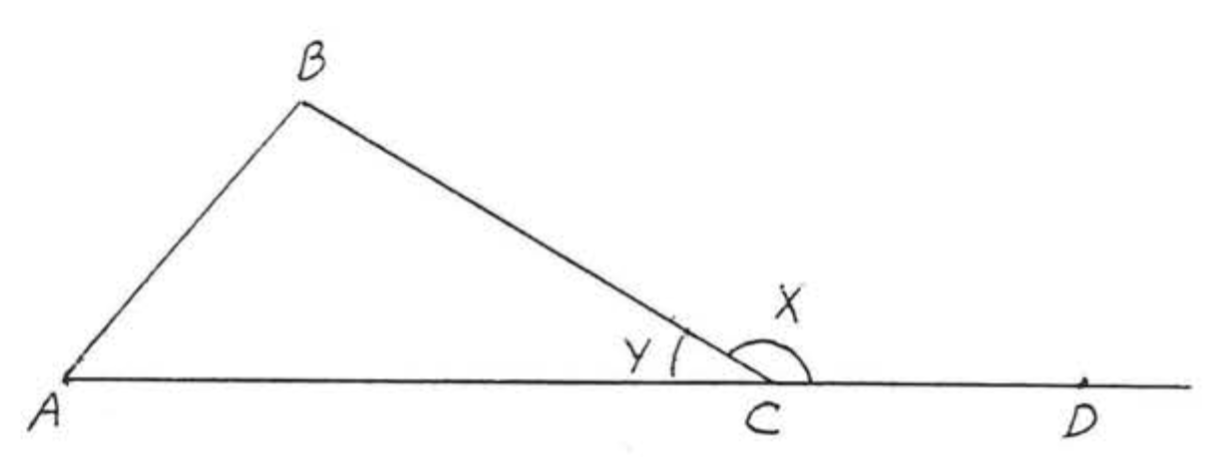
The results of Example \(\PageIndex{3}\) suggest the following theorem.
An exterior angle is equal to the sum of the two remote interior angles,
In Figure \(\PageIndex{4}\), \(\angle x = \angle A + \angle B\).
Find \(x\):
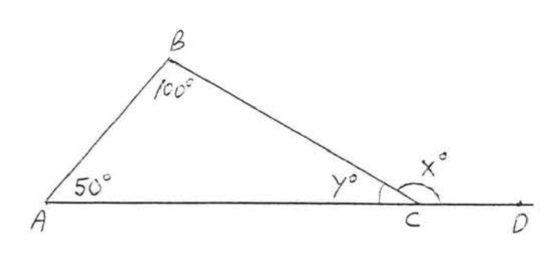
Solution
Using Theorem \(\PageIndex{2}\), \(x^{\circ} = 100^{\circ} + 50^{\circ} = 150^{\circ}\).
Answer: \(x = 150\).
Proof of Theorem \(\PageIndex{2}\): We present this proof in double-column form, with statements in the left column and the reason for each statement in the right column. The last statement is the theorem we wish to prove.
| Statements | Reasons |
| 1. \(\angle A + \angle B + \angle y = 180^{\circ}\) | 1. The sum of the angles of a triangle is \(180^{\circ}\). |
| 2. \(\angle A + \angle B = 180^{\circ} - \angle y\) | 2. Subtract \(\angle y\) from both sides of the equation, statement 1. |
| 3. \(\angle x = 180^{\circ} - \angle y.\) | 3. \(\angle x\) and \(\angle y\) are supplementary. |
| 4. \(\angle x = \angle A + \angle B\). | 4. Both \(\angle x\) (statement 3) and \(\angle A + \angle B\) (statement 2) equal \(180^{\circ} - \angle y\). |
Find \(x\):
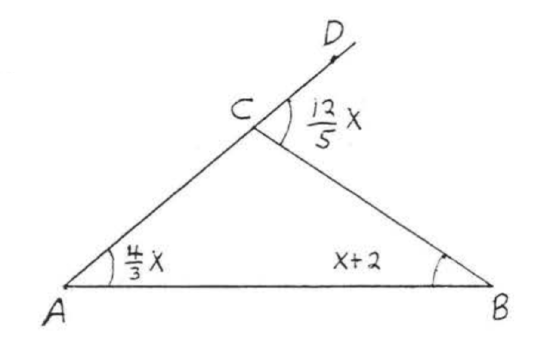
Solution
\(\angle BCD\) is an exterior angle with remote interior angles \(\angle A\) and \(\angle B\). By Theorem \(\PageIndex{2}\),
\[\begin{array} {rcl} {\angle BCD} & = & {\angle A + \angle B} \\ {\dfrac{12}{5} x} & = & {\dfrac{4}{3} x + x + 2} \end{array}\]
The least common denominator (1, c, d) is 15.
\[\begin{array} {rcl} {\begin{array} {c} {^3} \\ {(\cancel{15})} \end{array} \dfrac{12}{\cancel{5}} x} & = & {\begin{array} {c} {^3} \\ {(\cancel{15})} \end{array} \dfrac{4}{\cancel{3}} x + (15)x + (15)(2)} \\ {36x} & = & {20x + 15x + 30} \\ {36x} & = & {35x + 30} \\ {36x - 35x} & = & {30} \\ {x} & = & {30} \end{array} \nonumber\]
Check:
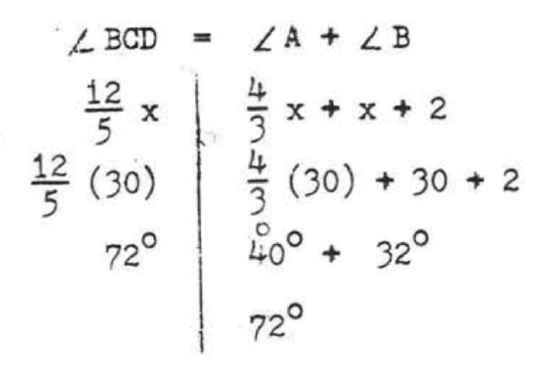
Answer: \(x = 30\).
Our work on the sum of the angles of a triangle can easily be extended to other figures:
Find the sum of the angles of a quadrilateral (four sided figure),
Solution
Divide the quadrilateral into two triangles as illustrated,
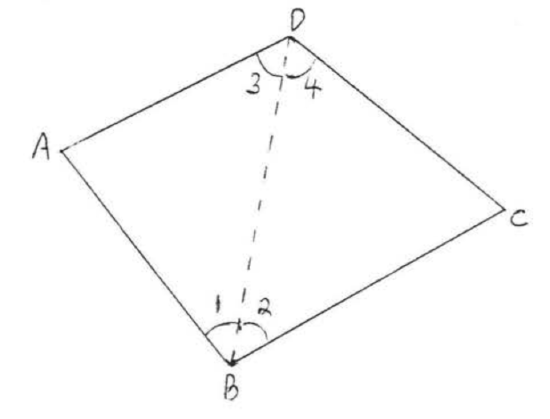
\[\begin{array} {rcl} {\angle A + \angle B + \angle C + \angle D} & = & {\angle A + \angle 1 + \angle 3 + \angle 2 + \angle 4 + \angle C} \\ {} & = & {180^{\circ} + 180^{\circ}} \\ {} & = & {360^{\circ}} \end{array} \nonumber\]
Answer: \(360^{\circ}\).
Find the sum of the angles of a pentagon (five-sided figure).
Solution
Divide the pentagon into three triangles as illustrated, The sum is equal to the sum of the angles of the three triangle = \((3)(180^{\circ}) = 540^{\circ}\).
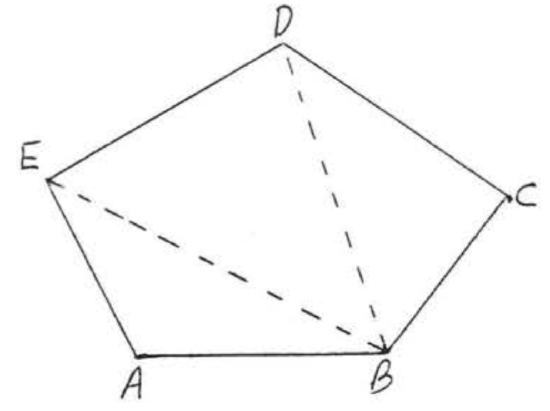
Answer: \(540^{\circ}\).
There is one more simple principle which we will derive from Theorem \(\PageIndex{1}\), Consider the two triangles in Figure \(\PageIndex{5}\).
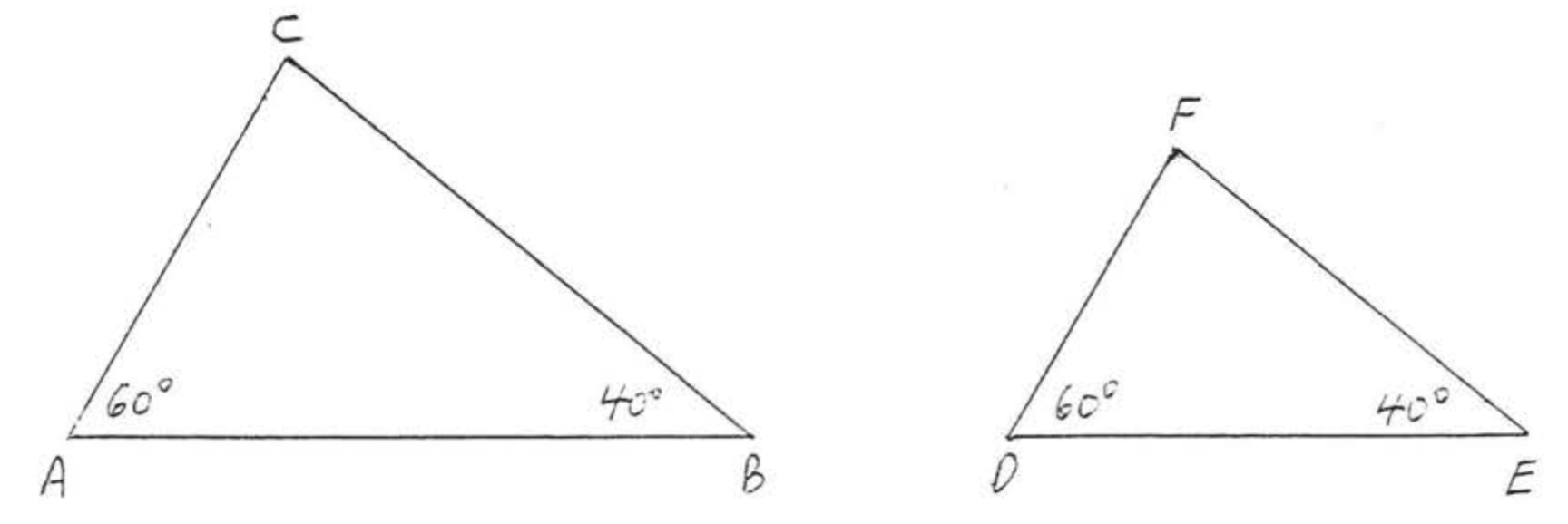
We are given that \(\angle A = \angle D = 60^{\circ}\) and \(\angle B = \angle E = 40^{\circ}\). A short calculation shows that we must also have \(\angle C = \angle F = 80^{\circ}\). This suggests the following theorem:
If two angles of one triangle are equal respectively to two angles of another triangle, then their remaining angles are also equal.
In Figure \(\PageIndex{6}\), if \(\angle A = \angle D\) and \(\angle B = \angle E\) then \(\angle C = \angle F\).
- Proof
-
\(\angle C = 180^{\circ} - (\angle A + \angle B) = 180^{\circ} - (\angle D + \angle E) = \angle F\).
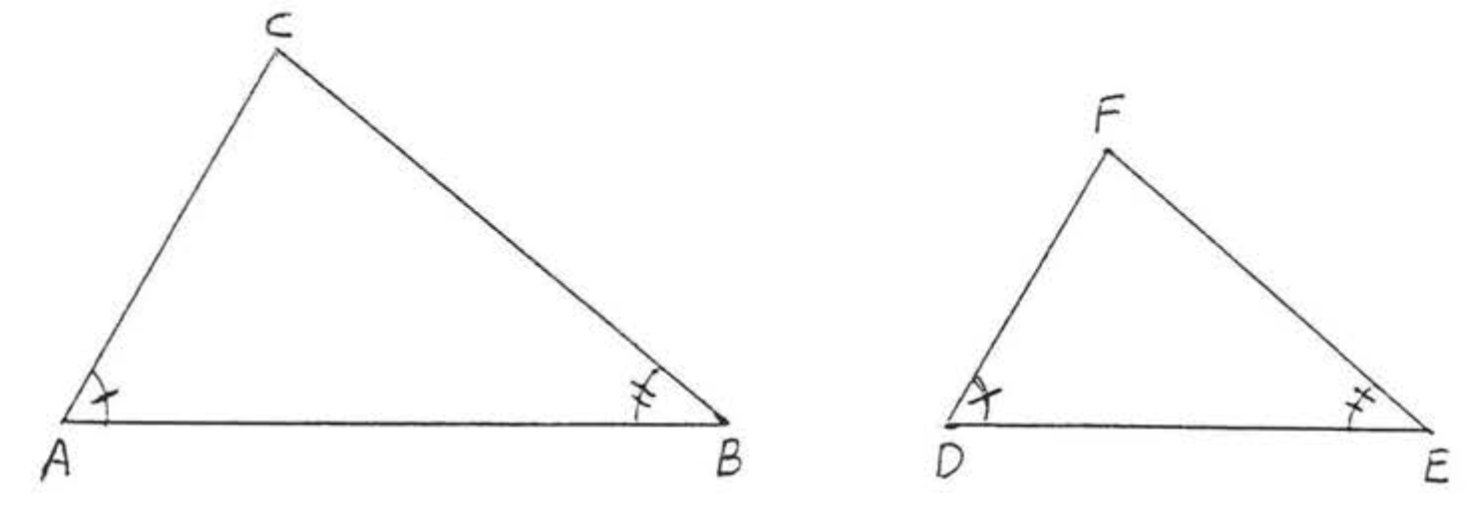
Figure \(\PageIndex{6}\). \(\angle A = \angle D\) and \(\angle B = \angle E\).
Our Theorem \(\PageIndex{1}\), which states that the sum of the angles of a triangle is \(180^{\circ}\), is one of the most important consequences of the parallel postulate, Therefore, one way of testing the truth of the parallel postulate (see the Historical Note in Section 1.4) is to test the truth of Theorem \(\PageIndex{1}\), This was actually tried by the German mathematician, astronomer, and physicist, Karl Friedrich Gauss (1777 - 1855). (This is the same Gauss whose name is used as a unit of measurement in the theory of magnetism), Gauss measured the sum of the angles of the triangle formed by three mountain peaks in Germany, He found the sum of the angles to be 14.85 seconds more than \(180^{\circ}\) (60 seconds 1 minute, 60 minutes = 1 degree). However this small excess could have been due to experimental error, so the sum might actually have been \(180^{\circ}\).
Aside from experimental error, there is another difficulty involved in verifying the angle sum theorem. According to the non-Euclidean geometry of Lobachevsky, the sum of the angles of a triangle is always less than \(180^{\circ}\). In the non-Euclidean geometry of Riemann, the sum of the angles is always more than \(180^{\circ}\), However in both cases the difference from \(180^{\circ}\) is insignificant unless the triangle is very large, Neither theory tells us exactly how large such a triangle should be, Even if we measured the angles of a very large triangle, like one formed by three stars, and found the sum to be indistinguishable from \(180^{\circ}\), we could only say that the angle sum theorem and parallel postulate are apparently true for these large distances, These distances still might be too small to enable us to determine whichgeometric system best describes the universe as a whole,
Problems
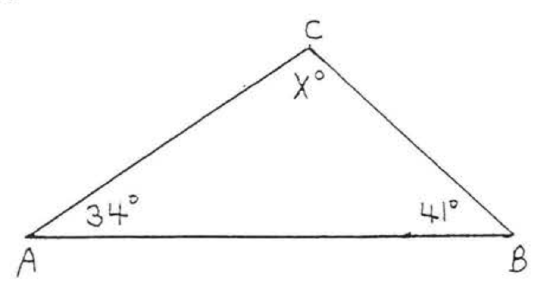
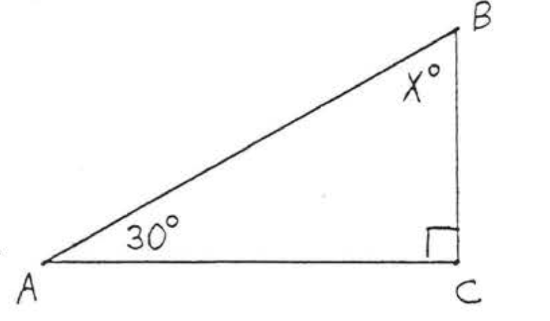
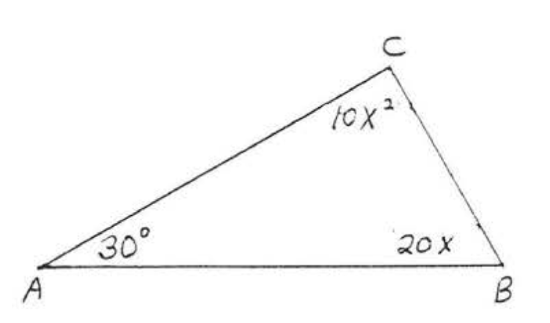
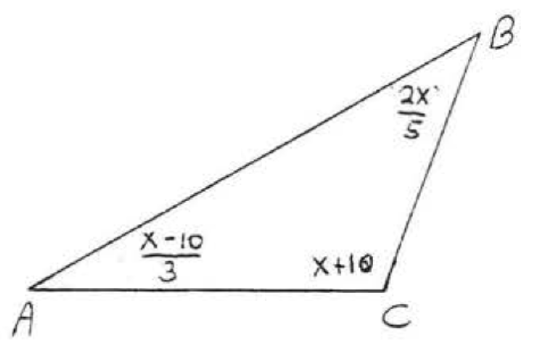
1 - 12. Find \(x\) and all the missing angles of each triangle:
1. 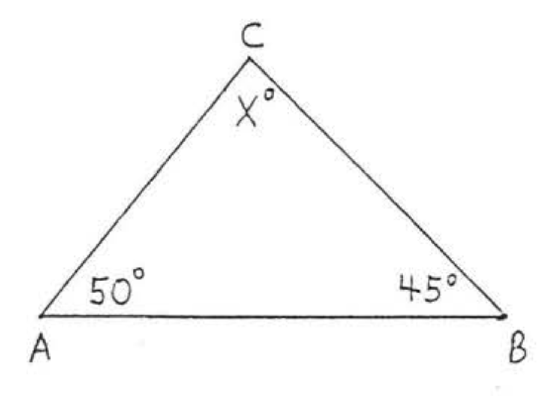 2.
2. 
3. 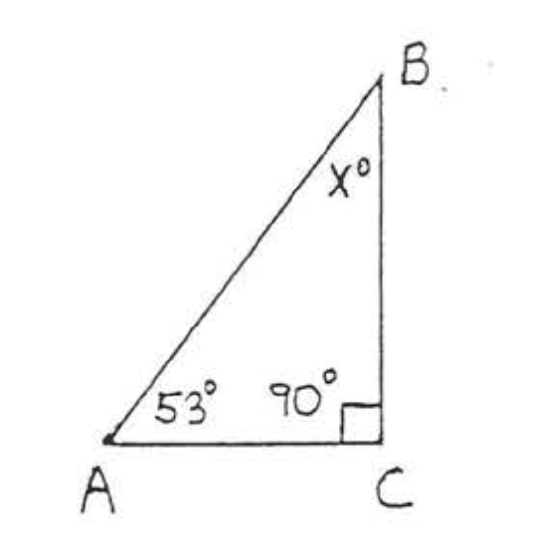 4.
4. 
5. 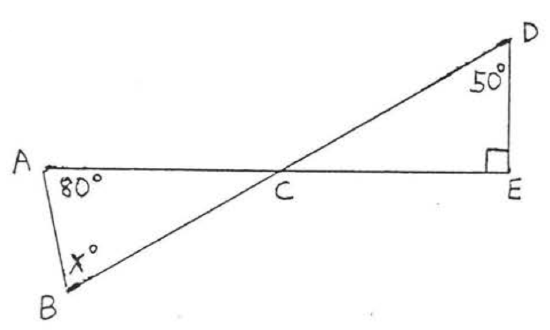 6.
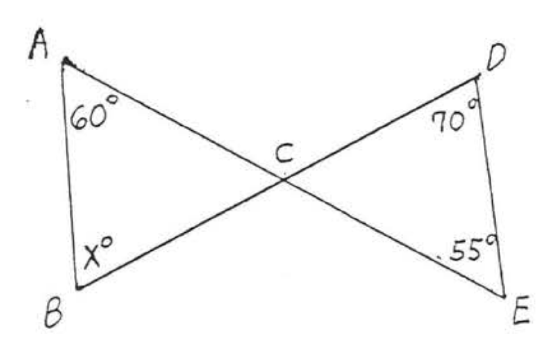
6. 
7. 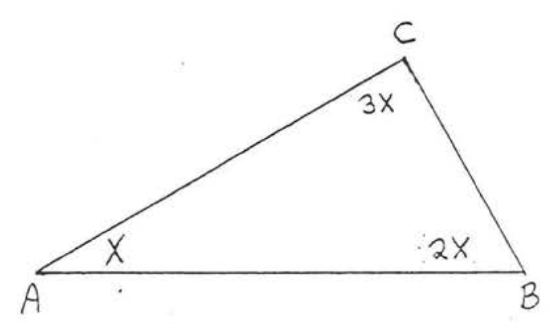 8.
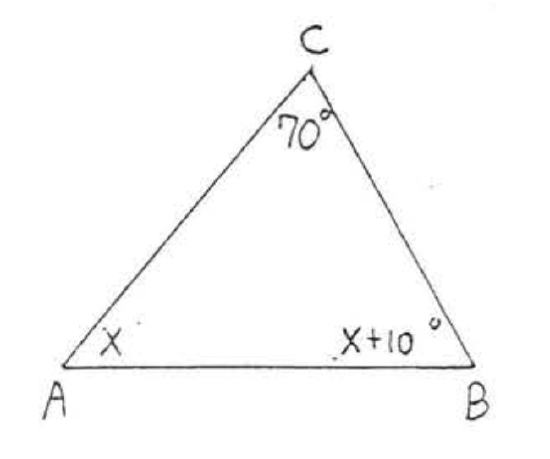
8. 
9. 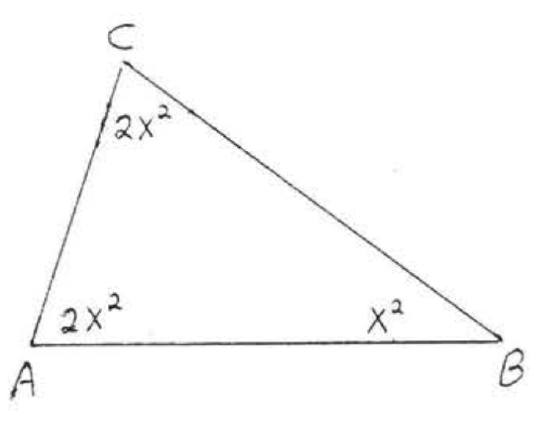 10.
10. 
11. 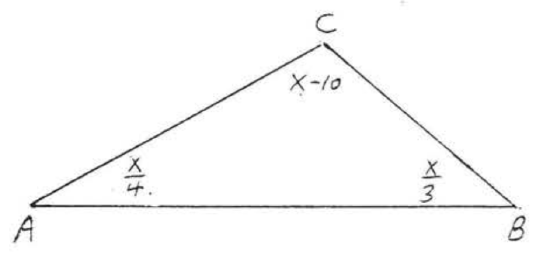 12.
12. 
13 - 14. Find \(x, y\), and \(z\):
13. 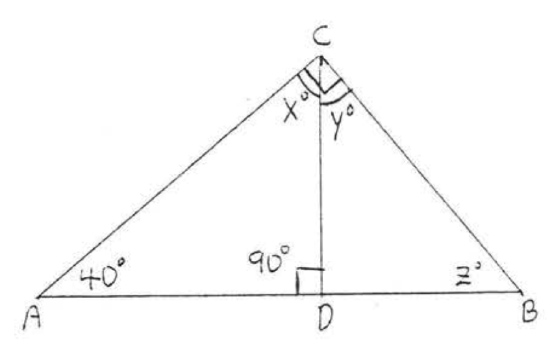 14.
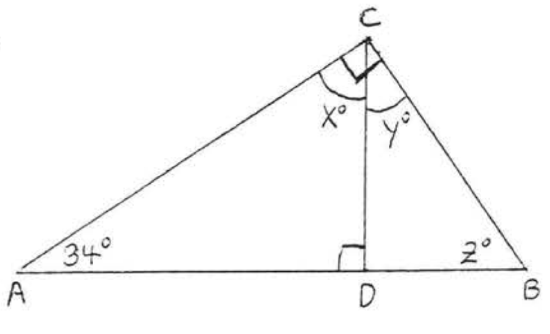
14. 
15 - 20. Find \(x\):
15. 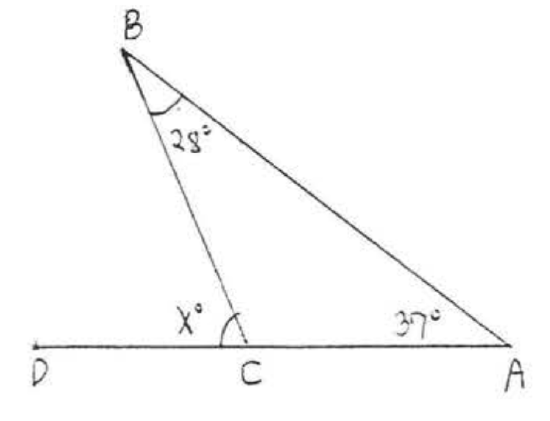 16.
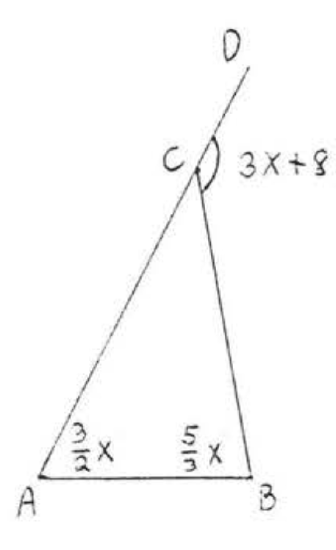
16. 
17. 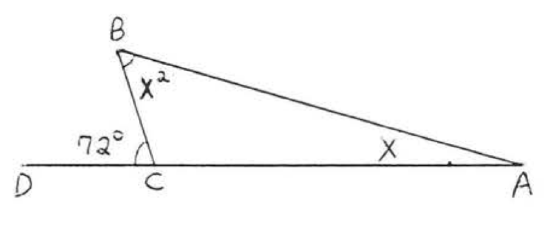 18.
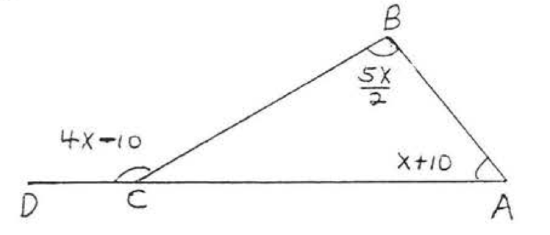
18. 
19. 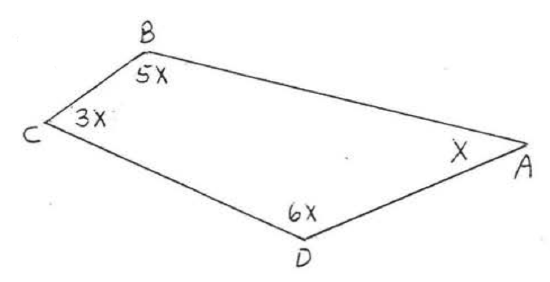 20.
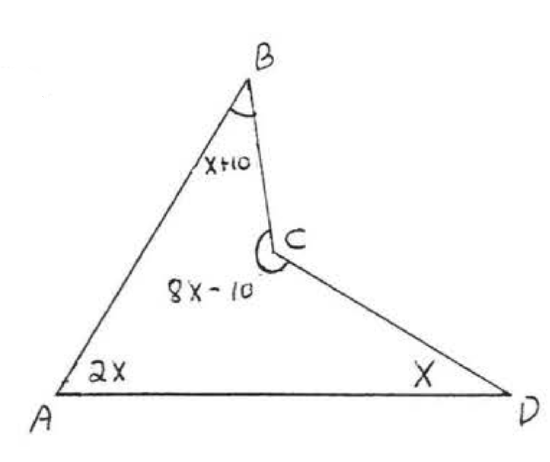
20. 
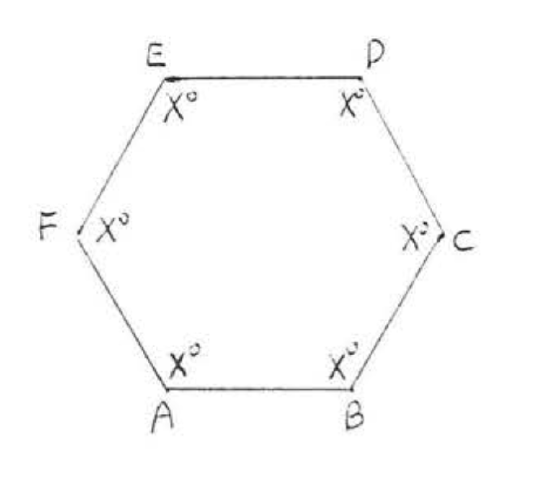
21. Find the sum of the angles of a hexagon (6-sided figure).
22. Find the sum of the angles of an octagon (8-sided figure).
23 - 26. Find \(x\):
23. 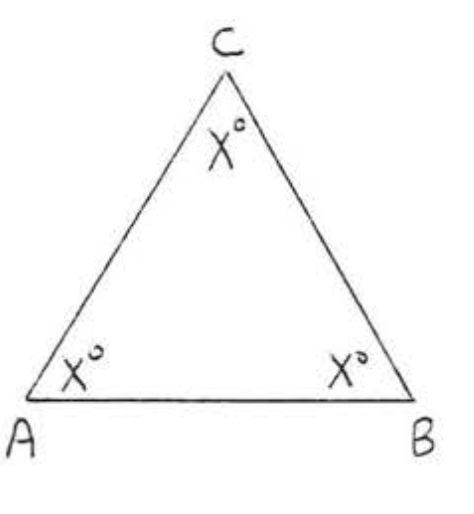 24.
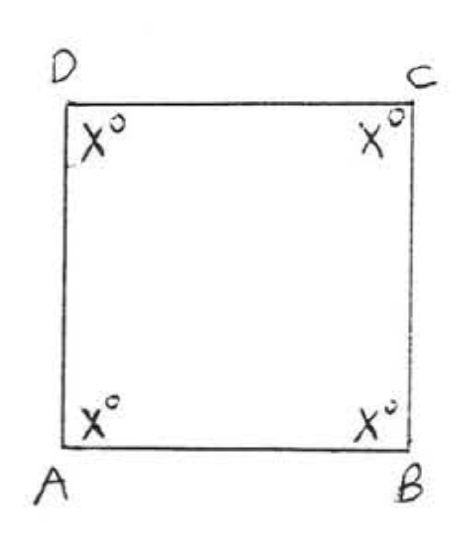
24. 
25. 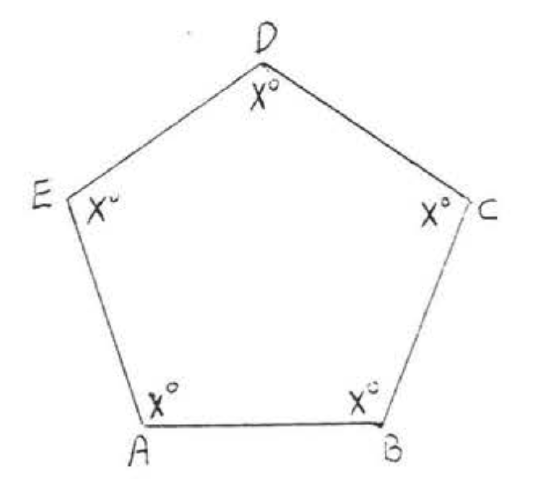 26.
26.