2.6: The SSS Theorem

We now consider the case where the side of two triangles are known to be of the same length.

Theorem $\PageIndex{1}$: Side-Side-Side (SSS) Theorem

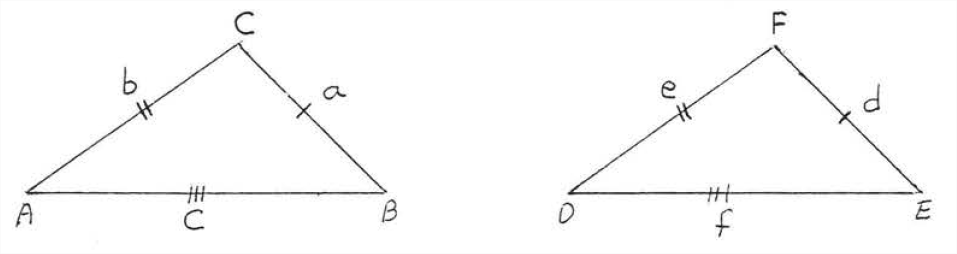
Two triangles are congruent if three sides of one are equal respectively to three sides of the other ($SSS = SSS$).

Theorem $\PageIndex{1}$ is demonstrated in Figure $\PageIndex{1}$: if $a=d, b=e,$ and $c=f$ then $\triangle ABC \cong \triangle DEF$

Figure $\PageIndex{1}$: $\triangle ABC \cong \triangle DEF$ because $SSS = SSS$.

Example $\PageIndex{1}$

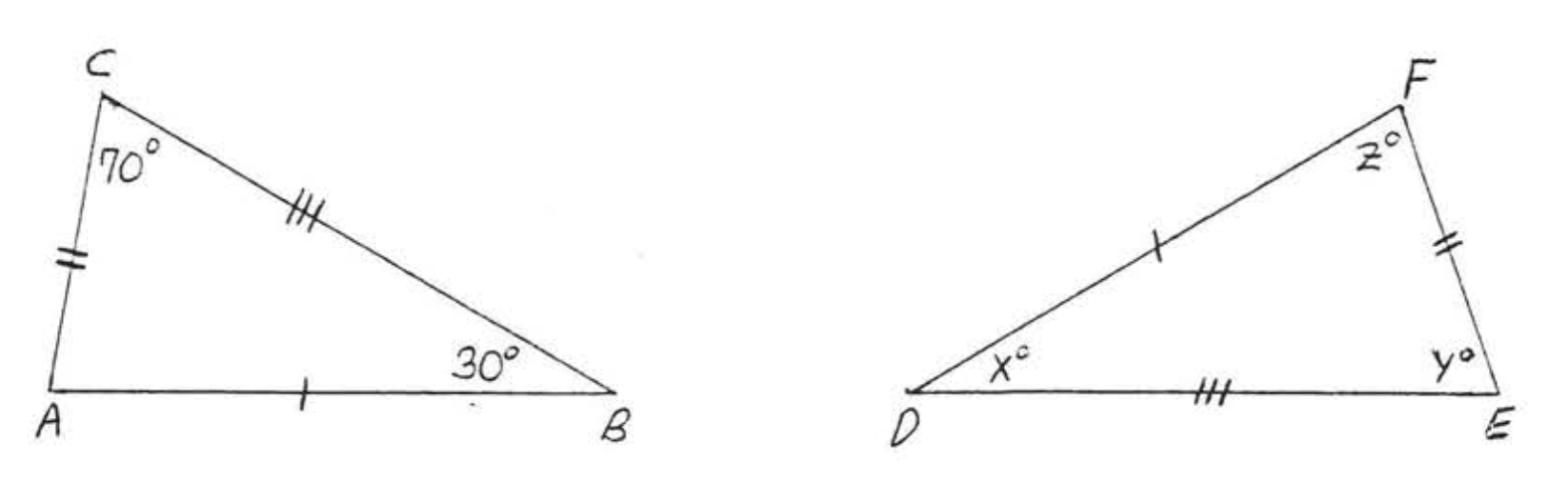
Find $x, y, z:$

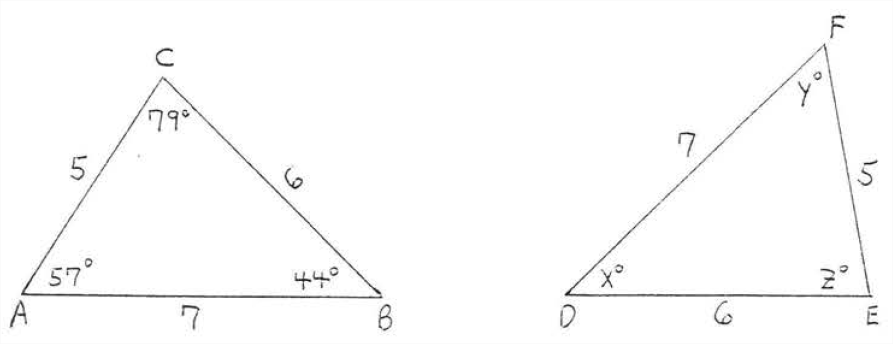
Solution

$AB = 7 = DF$. Therefore $\angle C,$ the angle opposite AB must correspond to $\angle E$, the angle opposite $DF$. In the same way $\angle A$ corresponds to $\angle F$ and $\angle B$ corresponds to $\angle D$. We have $\triangle ABC \cong \triangle FDE$ by $SSS = SSS$, so

$x^{\circ}=\angle D=\angle B=44^{\circ}$

$y^{\circ}=\angle F=\angle A=57^{\circ}$

$z^{\circ}=\angle E=\angle C=79^{\circ}$

Answer: $x = 44, y=57, z=79$

Proof of Theorem $\PageIndex{1}$

In Figure $\PageIndex{1}$, place $\triangle ABC$ and $\triangle DEF$ so that their longest sides coincide, in this case $AB$ and $DE$. This can be done because $AB = c= r = DE.$ Now draw $CF$, forming angles $1,2,3,$ and 4 (Figure $\PageIndex{2}$). The rest of the proof will be presented in double-column form:

Figure $\PageIndex{2}$: Place $\triangle ABC$ and $\triangle DEF$ so that $AB$ and DE coincide and draw $CF$.

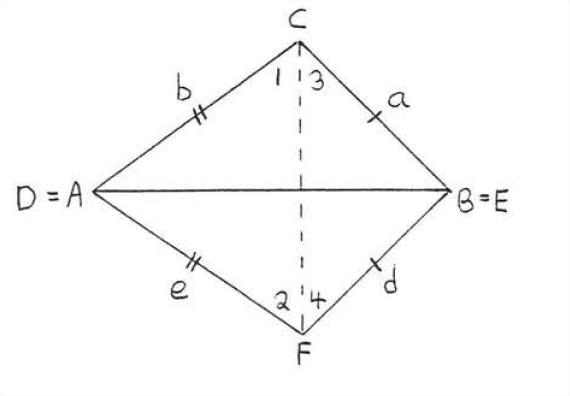
Statement	Reasons
1. $\angle 1 = \angle 2$.	1. The base angles of isosceles triangle $CAF$ are equal (Theorem $\PageIndex{1}$, section 2.5).
2. $\angle 3 = \angle 4$.	2. The base angles of isosceles triangle $CBF$ are equal.
3. $\angle C = \angle F$.	3. $\angle C = \angle 1 + \angle 3 = \angle 2 + \angle 4 = \angle F$.
4. $AC = DF$.	4. Given, $AC = b = e = DF$.
5. $BC = EF$.	5. Given, $BC = a = d = EF$.
6. $\triangle ABC \cong \triangle DEF$.	6. $SAS = SAS$: $AC, \angle C, BC$ of $\triangle ABC = DF$, $\angle F$, $EF$ of $\triangle DEF$.

Example $\PageIndex{2}$

Given $AB = DE, BC = EF,$ and $AC = DF$. Prove $\angle C = \angle F$

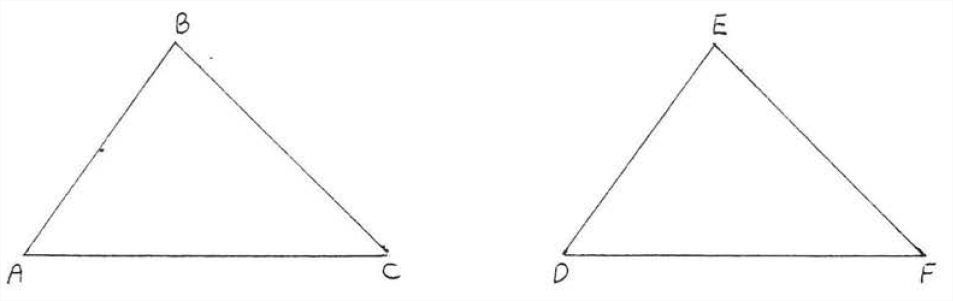
Solution

Statements	Reasons
1. $AB = DE$.	1. Given.
2. $BC = EF$.	2. Given.
3. $AC = DF$.	3. Given.
4. $\triangle ABC \cong \triangle DEF$.	4. $SSS = SSS$: $AB, BC, AC$ of $\triangle ABC = DE$, $EF, DF$ of $\triangle DEF$.
5. $\angle C = \angle F$.	5. Corresponding angles of congruent triangles are equal.

Application: Triangular Bracing

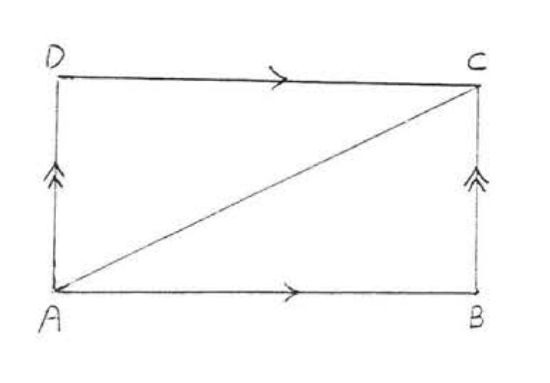
The SSS Theorem is the basis of an important principle of construction engineering called triangular bracing. Imagine the line segments in Figure $\PageIndex{3}$ to be beans of wood or steel joined at the endpoints by nails or screws. If pressure is applied to one of the sides, $ABCD$ will collapse and look like $A'B'C'D'$.

Figure $\PageIndex{3}$: $ABCD$ collapses into $A'B'C'D'$, when pressure is applied.

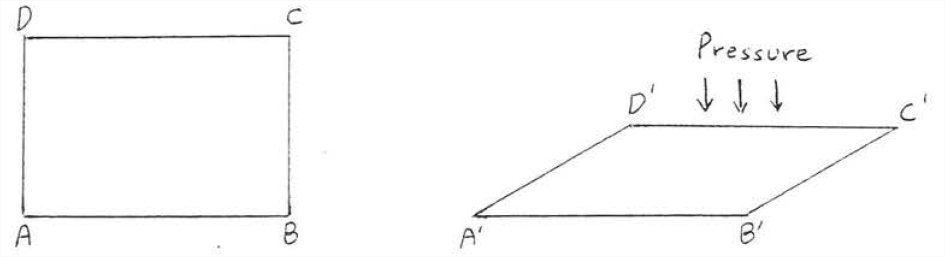
Now suppose points $A$ and $C$ are joined by a new beam, called a brace (Figure $\PageIndex{4}$). The structure will not collapse as long as the beans remain unbroken and joined together. It is impossible to deform $ABCD$ into any other shape $A'B'C'D'$ because if $AB = A'B'$, $BC = B'C'$, and $AC = A'C'$ then $\triangle ABC$ would be congruent to $\triangle A'B'C'$ by $SSS = SSS$.

Figure $\PageIndex{4}$: $ABCD$ cannot collapse into $A'B'C'D'$ as long as the beams remain unbroken and Jotned together.

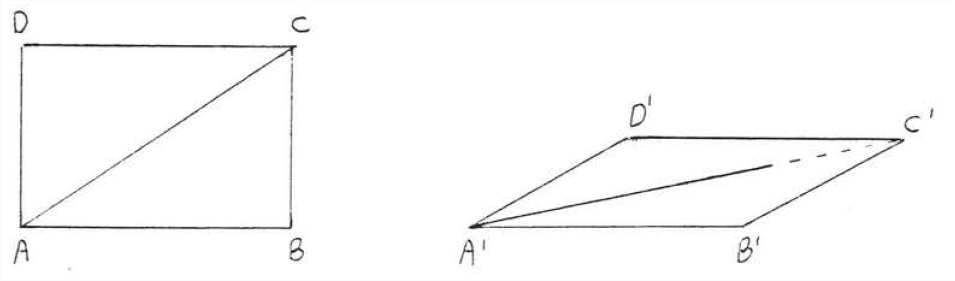
We sometimes say that a triangle is a rigid figure; once the sides of a triangle are fixed the angles cannot be changed. Thus in Figure $\PageIndex{4}$, the shape of $\triangle ABC$ cannot be changed as long as the lengths of its sides remain the same.

Problems

1 - 8. For each of the following (1) write the congruence statement,

(2) given the reason for (1) ($SAS$, $ASA$, $AAS$, or $SSS$ Theorem), and

(3) find $x$, or $x$ and $y$, or $x, y$, and $z$.

1.

2.

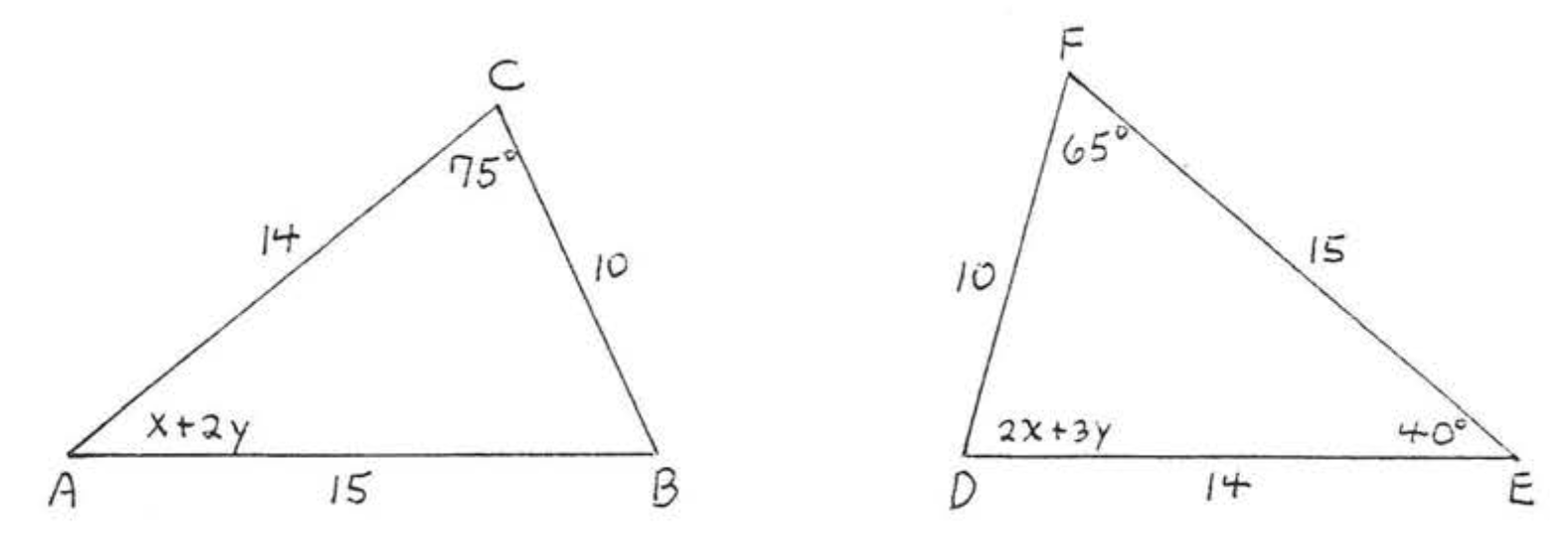
3.

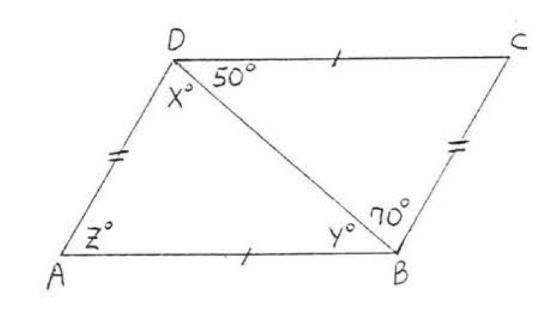
4.

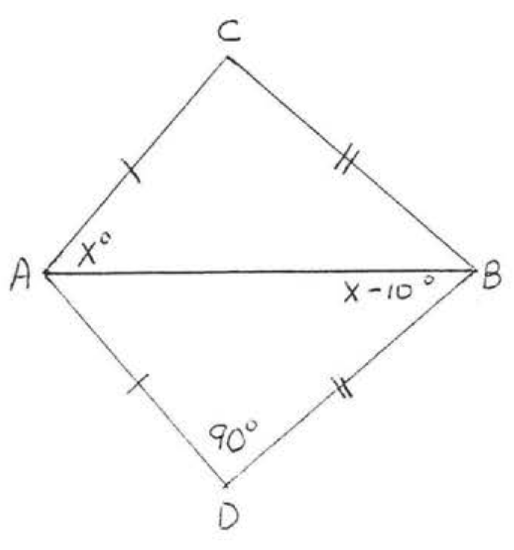
5.

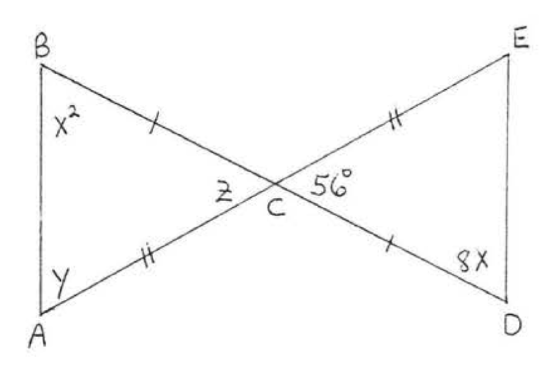
6.

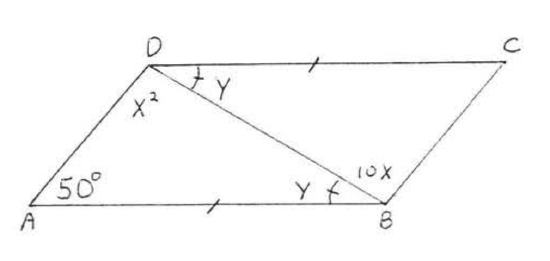
7.

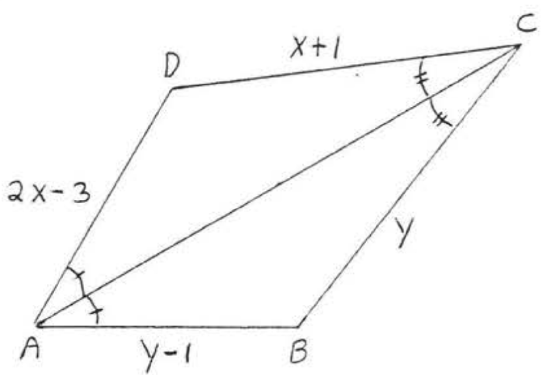
8.

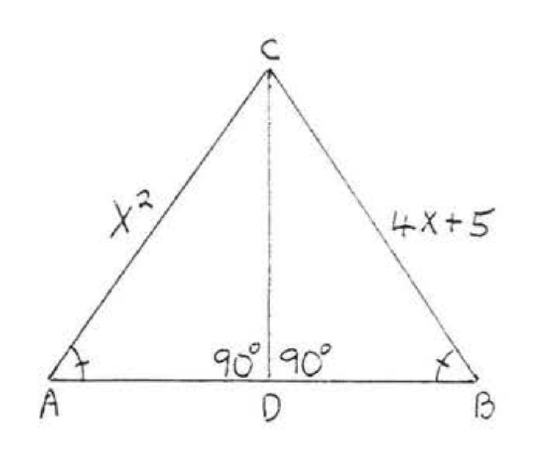
9. Given $AB = DE$, $BC = EF$, and $AC = DF$. Prove $\angle A = \angle D$.

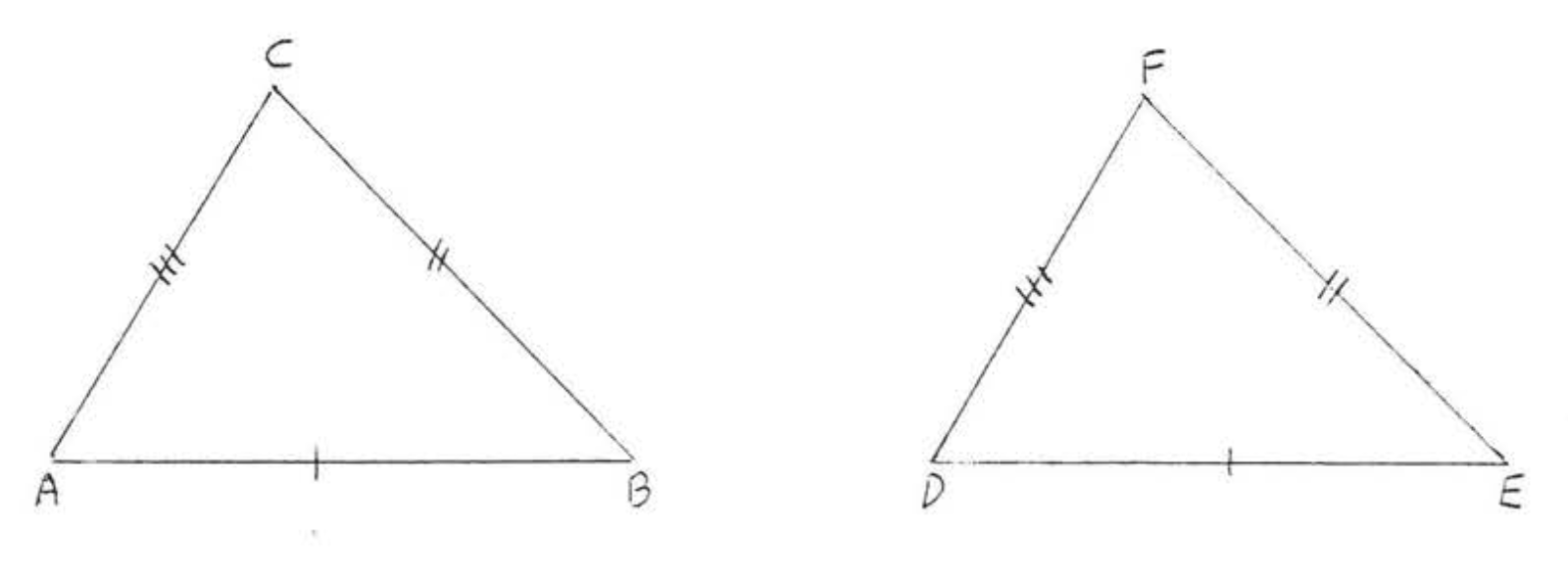
10. Given $AC = BC$. $AD = BD$. Prove $\angle ADC = \angle BDC$.

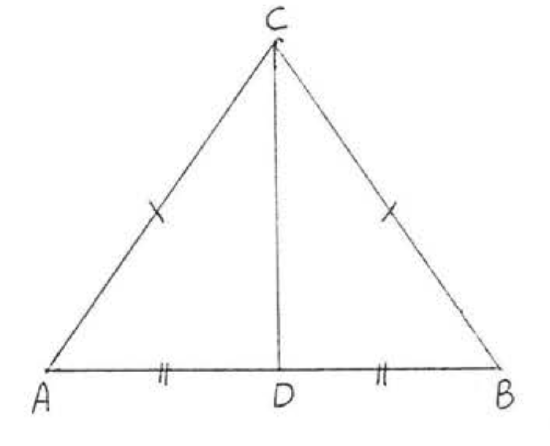
11. Given $AB = AD$, $BC = DC$. Prove $\angle BAC = \angle CAD$.

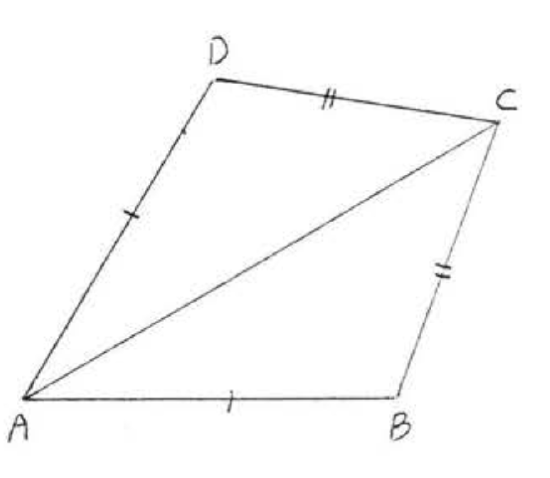
12. Given $AB = CD$, $BC = DA$. Prove $\angle BAC = \angle DCA$.

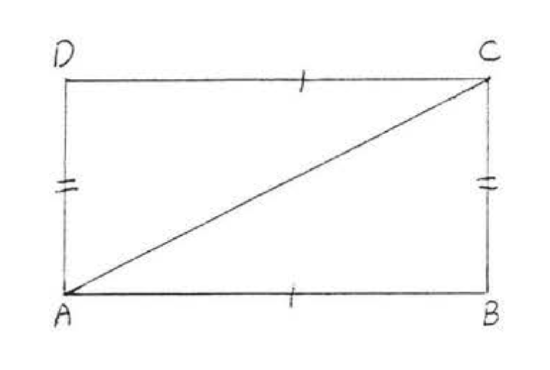
13. Given $AE = CE$, $BE = ED$. Prove $AB = CD$.

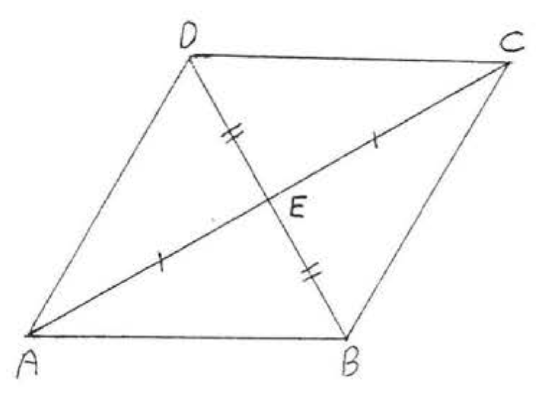
14. Given $AB||CD$, $AD||BC$. Prove $AB = CD$.