6.2: Polar Form
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Convert a complex number from standard form to polar form, and from polar form to standard form.
In the previous section, we identified a complex number z=a+bi with a point (a,b) in the coordinate plane. There is another form in which we can express the same number, called the polar form. The polar form is the focus of this section. It will turn out to be very useful if not crucial for certain calculations as we shall soon see.
Suppose z=a+bi is a complex number, and let r=√a2+b2=|z|. Recall that r is the modulus of z. Note first that (ar)2+(br)2=a2+b2r2=1
We often speak of the principal argument of z. This is the unique angle θ∈(−π,π] such that cosθ=ar, sinθ=br
The polar form of the complex number z=a+bi=r(cosθ+isinθ) is for convenience written as: z=reiθ
Let z=a+bi be a complex number. Then the polar form of z is written as z=reiθ
When given z=reiθ, the identity eiθ=cosθ+isinθ will convert z back to standard form. Here we think of eiθ as a short cut for cosθ+isinθ. This is all we will need in this course, but in reality eiθ can be considered as the complex equivalent of the exponential function where this turns out to be a true equality.
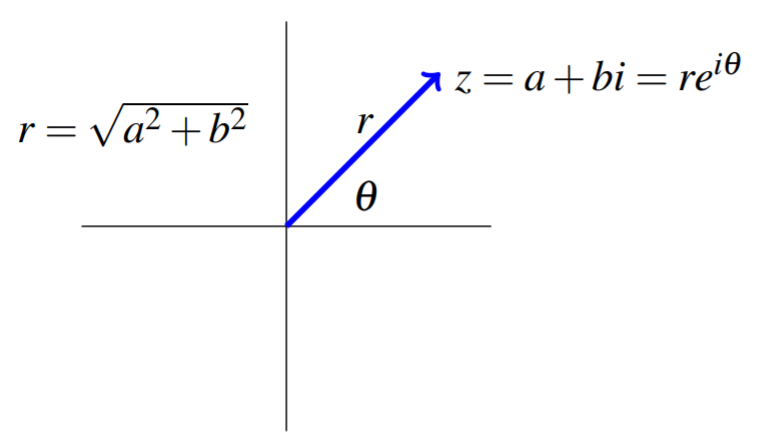
Thus we can convert any complex number in the standard (Cartesian) form z=a+bi into its polar form. Consider the following example.
Let z=2+2i be a complex number. Write z in the polar form z=reiθ
Solution
First, find r. By the above discussion, r=√a2+b2=|z|. Therefore, r=√22+22=√8=2√2
Now, to find θ, we plot the point (2,2) and find the angle from the positive x axis to the line between this point and the origin. In this case, θ=45∘=π4. That is we found the unique angle θ such that θ=cos−1(1/√2) and θ=sin−1(1/√2).
Note that in polar form, we always express angles in radians, not degrees.
Hence, we can write z as z=2√2eiπ4
Notice that the standard and polar forms are completely equivalent. That is not only can we transform a complex number from standard form to its polar form, we can also take a complex number in polar form and convert it back to standard form.
Let z=2e2πi/3. Write z in the standard form z=a+bi
Solution
Let z=2e2πi/3 be the polar form of a complex number. Recall that eiθ=cosθ+isinθ. Therefore using standard values of sin and cos we get: z=2ei2π/3=2(cos(2π/3)+isin(2π/3))=2(−12+i√32)=−1+√3i
You can always verify your answer by converting it back to polar form and ensuring you reach the original answer.


