2.5: Linear Independence

Last updated
Save as PDF

Page ID: 70190

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectives

Understand the concept of linear independence.
Learn two criteria for linear independence.
Understand the relationship between linear independence and pivot columns / free variables.
Recipe: test if a set of vectors is linearly independent / find an equation of linear dependence.
Picture: whether a set of vectors in $\mathbb{R}^2$ or $\mathbb{R}^3$ is linearly independent or not.
Vocabulary words: linear dependence relation / equation of linear dependence.
Essential vocabulary words: linearly independent, linearly dependent.

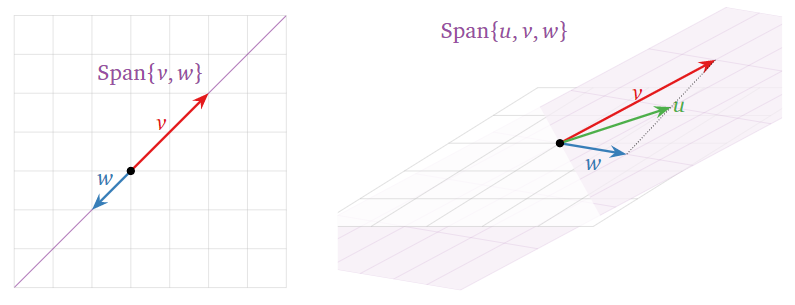
Sometimes the span of a set of vectors is “smaller” than you expect from the number of vectors, as in the picture below. This means that (at least) one of the vectors is redundant: it can be removed without affecting the span. In the present section, we formalize this idea in the notion of linear independence.

$clipboard_e983164810dc9ce7939b1f8561d406f55.png$

Figure $\PageIndex{1}$: Pictures of sets of vectors that are linearly dependent. Note that in each case, one vector is in the span of the others—so it doesn’t make the span bigger.

The Definition of Linear Independence

Definition $\PageIndex{1}$: Linearly Independent and Linearly Dependent

A set of vectors $\{v_1,v_2,\ldots,v_k\}$ is linearly independent if the vector equation

\[ x_1v_1 + x_2v_2 + \cdots + x_kv_k = 0 \nonumber \]

has only the trivial solution $x_1=x_2=\cdots=x_k=0$. The set $\{v_1,v_2,\ldots,v_k\}$ is linearly dependent otherwise.

In other words, $\{v_1,v_2,\ldots,v_k\}$ is linearly dependent if there exist numbers $x_1,x_2,\ldots,x_k\text{,}$ not all equal to zero, such that

\[ x_1v_1 + x_2v_2 + \cdots + x_kv_k = 0. \nonumber \]

This is called a linear dependence relation or equation of linear dependence.

Note: $\PageIndex{1}$

Note that linear dependence and linear independence are notions that apply to a collection of vectors. It does not make sense to say things like “this vector is linearly dependent on these other vectors,” or “this matrix is linearly independent.”

Example $\PageIndex{1}$: Checking linear dependence

Is the set

\[\left\{\left(\begin{array}{c}1\\1\\1\end{array}\right),\:\left(\begin{array}{c}1\\-1\\2\end{array}\right),\:\left(\begin{array}{c}3\\1\\4\end{array}\right)\right\}\nonumber\]

linearly independent?

Solution

Equivalently, we are asking if the homogeneous vector equation

\[x\left(\begin{array}{c}1\\1\\1\end{array}\right)+y\left(\begin{array}{c}1\\-1\\2\end{array}\right)+x\left(\begin{array}{c}3\\1\\4\end{array}\right)=\left(\begin{array}{c}0\\0\\0\end{array}\right)\nonumber\]

has a nontrivial solution. We solve this by forming a matrix and row reducing (we do not augment because of this Observation 2.4.2 in Section 2.4):

\[\left(\begin{array}{ccc}1&1&3 \\ 1&-1&1 \\ 1&2&4\end{array}\right) \quad\xrightarrow{\text{row reduce}}\quad \left(\begin{array}{ccc}1&0&2 \\ 0&1&1 \\ 0&0&0\end{array}\right)\nonumber\]

This says $x = -2z$ and $y = -z$. So there exist nontrivial solutions: for instance, taking $z=1$ gives this equation of linear dependence:

\[-2\left(\begin{array}{c}1\\1\\1\end{array}\right)-\left(\begin{array}{c}1\\-1\\2\end{array}\right)+\left(\begin{array}{c}3\\1\\4\end{array}\right)=\left(\begin{array}{c}0\\0\\0\end{array}\right).\nonumber\]

$clipboard_e3085588f24846f0815457370d946332d.png$

Figure $\PageIndex{2}$: Move the sliders to solve the homogeneous vector equation in this example. Do you see why the vectors need to be coplanar in order for there to exist a nontrivial solution?

Example $\PageIndex{2}$: Checking linear independence

Is the set

\[\left\{\left(\begin{array}{c}1\\1\\-2\end{array}\right),\:\left(\begin{array}{c}1\\-1\\2\end{array}\right),\:\left(\begin{array}{c}3\\1\\4\end{array}\right)\right\}\nonumber\]

linearly independent?

Solution

Equivalently, we are asking if the homogeneous vector equation

\[x\left(\begin{array}{c}1\\1\\-2\end{array}\right)+y\left(\begin{array}{c}1\\-1\\2\end{array}\right)+z\left(\begin{array}{z}3\\1\\4\end{array}\right)=\left(\begin{array}{c}0\\0\\0\end{array}\right)\nonumber\]

has a nontrivial solution. We solve this by forming a matrix and row reducing (we do not augment because of this Observation 2.4.2 in Section 2.4):

\[\left(\begin{array}{ccc}1&1&3 \\ 1&-1&1 \\ -2&2&4\end{array}\right) \quad\xrightarrow{\text{row reduce}}\quad \left(\begin{array}{ccc}1&0&0 \\ 0&1&0 \\ 0&0&1\end{array}\right)\nonumber\]

This says $x = y = z = 0\text{,}$ i.e., the only solution is the trivial solution. We conclude that the set is linearly independent.

$clipboard_e377ac11e1662115e5907de078150dda8.png$

Figure $\PageIndex{3}$: Move the sliders to solve the homogeneous vector equation in this example. Do you see why the vectors would need to be coplanar in order for there to exist a nontrivial solution?

Example $\PageIndex{3}$: Vector parametric form

An important observation is that the vectors coming from the parametric vector form of the solution of a matrix equation $Ax=0$ are linearly independent. In Example 2.4.4 we saw that the solution set of $Ax=0$ for

\[A=\left(\begin{array}{ccc}1&-1&2 \\ -2&2&-4\end{array}\right)?\nonumber\]

\[x=\left(\begin{array}{c}x_1 \\ x_2 \\ x_3\end{array}\right) =x_2\left(\begin{array}{c}1\\1\\0\end{array}\right)+x_3\left(\begin{array}{c}-2\\0\\1\end{array}\right).\nonumber\]

Let's explain why the vectors $(1,1,0)$ and $(-2,0,1)$ are linearly independent. Suppose that

\[\left(\begin{array}{c}0\\0\\0\end{array}\right) =x_2\left(\begin{array}{c}1\\1\\0\end{array}\right) +x_3\left(\begin{array}{c}-2\\0\\1\end{array}\right) =\left(\begin{array}{c} x_2 -2x_3 \\ x_2 \\ x_3\end{array}\right).\nonumber\]

Comparing the second and third coordinates, we see that $x_2=x_3=0$. This reasoning will work in any example, since the entries corresponding to the free variables are all equal to 1 or 0, and are only equal to 1 in one of the vectors. This observation forms part of this theorem in Section 2.7, Theorem 2.7.2.

The above examples lead to the following recipe.

Recipe: Checking Linear Independence

A set of vectors $\{v_1,v_2,\ldots,v_k\}$ is linearly independent if and only if the vector equation

\[ x_1v_1 + x_2v_2 + \cdots + x_kv_k = 0 \nonumber \]

has only the trivial solution, if and only if the matrix equation $Ax=0$ has only the trivial solution, where $A$ is the matrix with columns $v_1,v_2,\ldots,v_k\text{:}$

\[A=\left(\begin{array}{cccc}|&|&\quad &| \\ v_1 & v_2 &\cdots &v_k \\ |&|&\quad &|\end{array}\right).\nonumber\]

This is true if and only if $A$ has a pivot position, Definition 1.2.5 in Section 1.2 in every column.

Solving the matrix equatiion $Ax=0$ will either verify that the columns $v_1,v_2,\ldots,v_k$ are linearly independent, or will produce a linear dependence relation by substituting any nonzero values for the free variables.

(Recall that $Ax=0$ has a nontrivial solution if and only if $A$ has a column without a pivot: see this Observation 2.4.1 in Section 2.4.)

Suppose that $A$ has more columns than rows. Then $A$ cannot have a pivot in every column (it has at most one pivot per row), so its columns are automatically linearly dependent.

Note $\PageIndex{2}$

A wide matrix (a matrix with more columns than rows) has linearly dependent columns.

For example, four vectors in $\mathbb{R}^3$ are automatically linearly dependent. Note that a tall matrix may or may not have linearly independent columns.

Fact $\PageIndex{1}$: Facts About Linear Independence

Two vectors are linearly dependent if and only if they are collinear, i.e., one is a scalar multiple of the other.
Any set containing the zero vector is linearly dependent.
If a subset of $\{v_1,v_2,\ldots,v_k\}$ is linearly dependent, then $\{v_1,v_2,\ldots,v_k\}$ is linearly dependent as well.

Proof

If $v_1 = cv_2$ then $v_1-cv_2=0\text{,}$ so $\{v_1,v_2\}$ is linearly dependent. In the other direction, if $x_1v_1+x_2v_2=0$ with $x_1\neq0$ (say), then $v_1 = -\frac{x_2}{x_1}v_2$.
It is easy to produce a linear dependence relation if one vector is the zero vector: for instance, if $v_1=0$ then
\[ 1\cdot v_1 + 0\cdot v_2 + \cdots + 0\cdot v_k = 0. \nonumber \]
After reordering, we may suppose that $\{v_1,v_2,\ldots,v_r\}$ is linearly dependent, with $r < p$. This means that there is an equation of linear dependence \[ x_1v_1 + x_2v_2 + \cdots + x_rv_r = 0\text{,} \nonumber \] with at least one of $x_1,x_2,\ldots,x_r$ nonzero. This is also an equation of linear dependence among $\{v_1,v_2,\ldots,v_k\}\text{,}$ since we can take the coefficients of $v_{r+1},\ldots,v_k$ to all be zero.

With regard to the first fact, note that the zero vector is a multiple of any vector, so it is collinear with any other vector. Hence facts 1 and 2 are consistent with each other.

Criteria for Linear Independence

In this subsection we give two criteria for a set of vectors to be linearly independent. Keep in mind, however, that the actual definition for linear independence, Definition $\PageIndex{1}$, is above.

Theorem $\PageIndex{1}$

A set of vectors $\{v_1,v_2,\ldots,v_k\}$ is linearly dependent if and only if one of the vectors is in the span of the other ones.

Any such vector may be removed without affecting the span.

Proof

Suppose, for instance, that $v_3$ is in $\text{Span}\{v_1,v_2,v_4\}\text{,}$ so we have an equation like

\[ v_3 = 2v_1 - \frac 12v_2 + 6v_4. \nonumber \]

We can subract $v_3$ from both sides of the equation to get

\[ 0 = 2v_1 - \frac 12v_2 - v_3 + 6v_4. \nonumber \]

This is a linear dependence relation.

In this case, any linear combination of $v_1,v_2,v_3,v_4$ is already a linear combination of $v_1,v_2,v_4\text{:}$

\[\begin{aligned} x_1v_1 + x_2v_2 + x_3v_3 + x_4v_4 &= x_1v_1 + x_2v_2 + x_3\left(2v_1-\frac 12v_2 + 6v_4\right) + x_4v_4\\ &= (x_1+2x_3)v_1 + \left(x_2-\frac 12x_3\right)v_2 + (x_4+6)v_4. \end{aligned}\]

Therefore, $\text{Span}\{v_1,v_2,v_3,v_4\}$ is contained in $\text{Span}\{v_1,v_2,v_4\}$. Any linear combination of $v_1,v_2,v_4$ is also a linear combination of $v_1,v_2,v_3,v_4$ (with the $v_3$-coefficient equal to zero), so $\text{Span}\{v_1,v_2,v_4\}$ is also contained in $\text{Span}\{v_1,v_2,v_3,v_4\}\text{,}$ and thus they are equal.

In the other direction, if we have a linear dependence relation like

\[ 0 = 2v_1 - \frac 12v_2 + v_3 - 6v_4, \nonumber \]

then we can move any nonzero term to the left side of the equation and divide by its coefficient:

\[ v_1 = \frac 12\left(\frac 12v_2 - v_3 + 6v_4\right). \nonumber \]

This shows that $v_1$ is in $\text{Span}\{v_2,v_3,v_4\}$.

We leave it to the reader to generalize this proof for any set of vectors.

Note $\PageIndex{3}$

In a linearly dependent set $\{v_1,v_2,\ldots,v_k\}\text{,}$ it is not generally true that any vector $v_j$ is in the span of the others, only that at least one of them is.

For example, the set $\bigl\{{1\choose 0},\,{2\choose 0},\,{0\choose 1}\bigr\}$ is linearly dependent, but ${0\choose 1}$ is not in the span of the other two vectors. Also see this Figure $\PageIndex{14}$ below.

The previous Theorem $\PageIndex{1}$ makes precise in what sense a set of linearly dependent vectors is redundant.

Theorem $\PageIndex{2}$: Increasing Span Criterion

A set of vectors $\{v_1,v_2,\ldots,v_k\}$ is linearly independent if and only if, for every $j\text{,}$ the vector $v_j$ is not in $\text{Span}\{v_1,v_2,\ldots,v_{j-1}\}$.

Proof

It is equivalent to show that $\{v_1,v_2,\ldots,v_k\}$ is linearly dependent if and only if $v_j$ is in $\text{Span}\{v_1,v_2,\ldots,v_{j-1}\}$ for some $j$. The “if” implication is an immediate consequence of the previous Theorem $\PageIndex{1}$. Suppose then that $\{v_1,v_2,\ldots,v_k\}$ is linearly dependent. This means that some $v_j$ is in the span of the others. Choose the largest such $j$. We claim that this $v_j$ is in $\text{Span}\{v_1,v_2,\ldots,v_{j-1}\}$. If not, then

\[ v_j = x_1v_1 + x_2v_2 + \cdots + x_{j-1}v_{j-1} + x_{j+1}v_{j+1} + \cdots + x_kv_k \nonumber \]

with not all of $x_{j+1},\ldots,x_k$ equal to zero. Suppose for simplicity that $x_k\neq 0$. Then we can rearrange:

\[ v_k = -\frac 1{x_k}\bigl( x_1v_1 + x_2v_2 + \cdots + x_{j-1}v_{j-1} - v_j + x_{j+1}v_{j+1} + \cdots + x_{p-1}v_{p-1} \bigr). \nonumber \]

This says that $v_k$ is in the span of $\{v_1,v_2,\ldots,v_{p-1}\}\text{,}$ which contradicts our assumption that $v_j$ is the last vector in the span of the others.

We can rephrase this as follows:

Note $\PageIndex{4}$

If you make a set of vectors by adding one vector at a time, and if the span got bigger every time you added a vector, then your set is linearly independent.

Pictures of Linear Independence

A set containg one vector $\{v\}$ is linearly independent when $v\neq 0\text{,}$ since $xv = 0$ implies $x=0$.

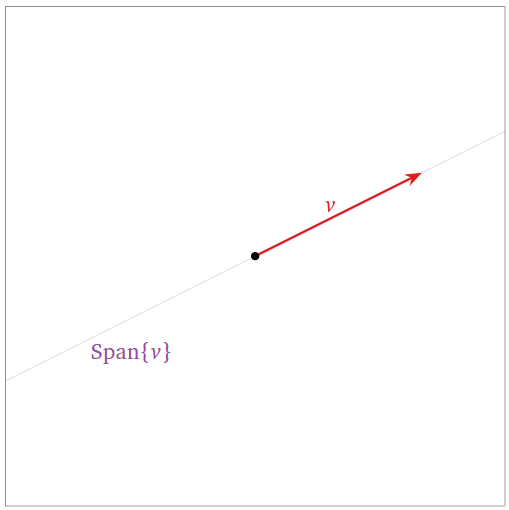
$clipboard_e63890d009191c7095787304a657fb2e6.png$

Figure $\PageIndex{4}$

A set of two noncollinear vectors $\{v,w\}$ is linearly independent:

Neither is in the span of the other, so we can apply the first criterion, Theorem $\PageIndex{1}$.
The span got bigger when we added $w\text{,}$ so we can apply the increasing span criterion, Theorem $\PageIndex{2}$.

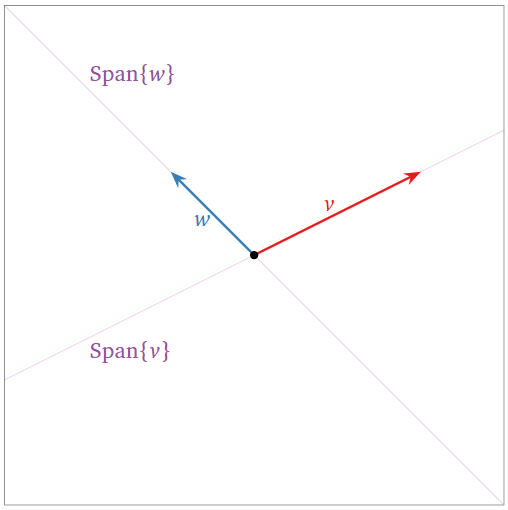
$clipboard_e86914c759da79eec627ffc96d524e7ee.png$

Figure $\PageIndex{5}$

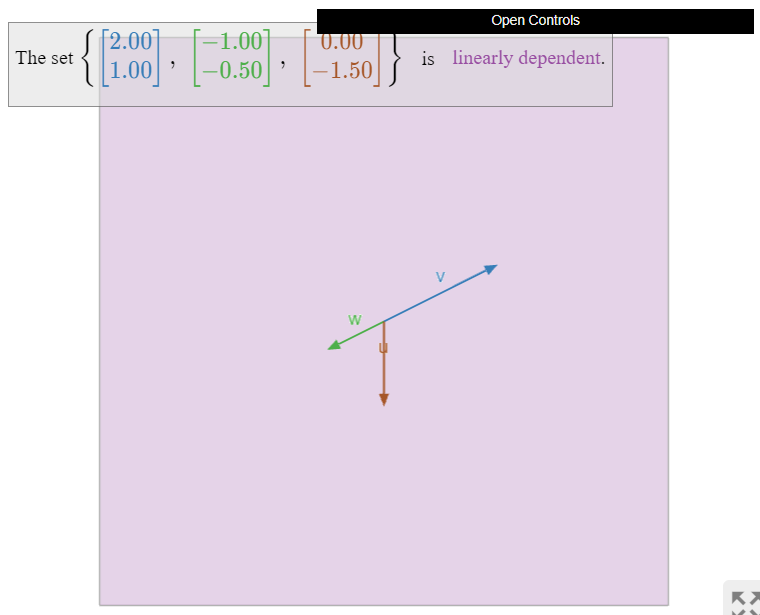
The set of three vectors $\{v,w,u\}$ below is linearly dependent:

$u$ is in $\text{Span}\{v,w\}\text{,}$ so we can apply the first criterion, Theorem $\PageIndex{1}$.
The span did not increase when we added $u\text{,}$ so we can apply the increasing span criterion, Theorem $\PageIndex{2}$.

In the picture below, note that $v$ is in $\text{Span}\{u,w\}\text{,}$ and $w$ is in $\text{Span}\{u,v\}\text{,}$ so we can remove any of the three vectors without shrinking the span.

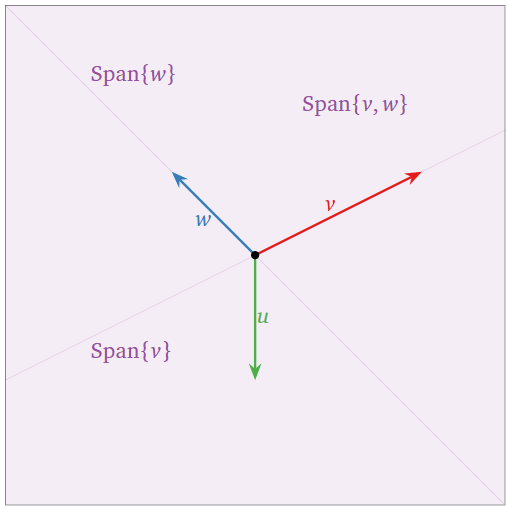
$clipboard_ecfcee67f120e0b88ff771ca0c41a416c.png$

Figure $\PageIndex{6}$

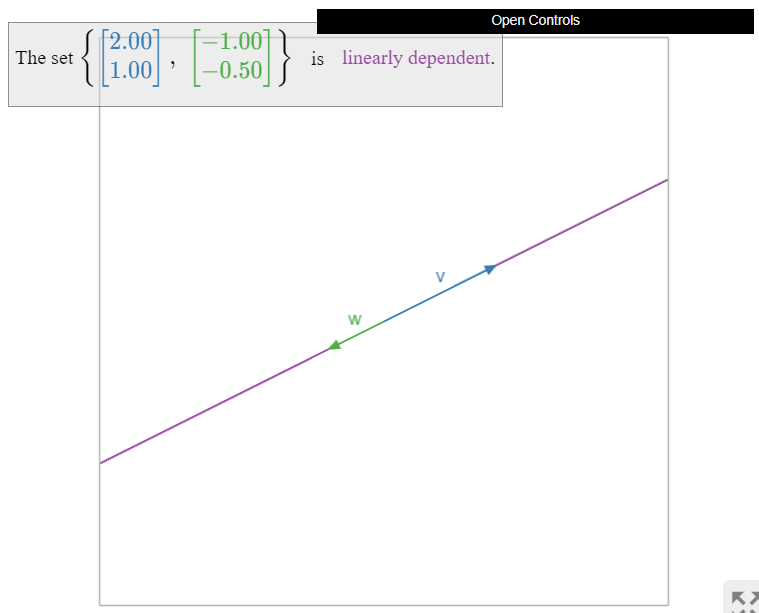
Two collinear vectors are always linearly dependent:

$w$ is in $\text{Span}\{v\}\text{,}$ so we can apply the first criterion, Theorem $\PageIndex{1}$.
The span did not increase when we added $w\text{,}$ so we can apply the increasing span criterion, Theorem $\PageIndex{2}$.

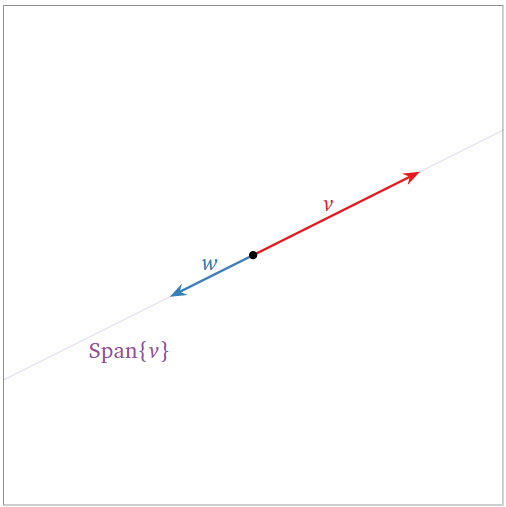
$clipboard_e5384f427cd9950249127c35faa3b1e26.png$

Figure $\PageIndex{7}$

These three vectors $\{v,w,u\}$ are linearly dependent: indeed, $\{v,w\}$ is already linearly dependent, so we can use the third Fact $\PageIndex{1}$.

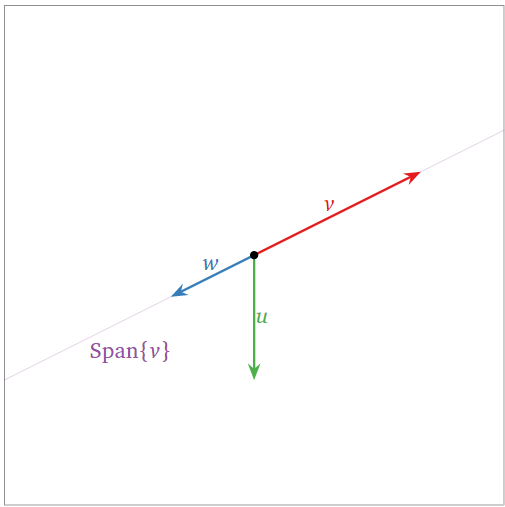
$clipboard_ef976f7b119abf3b375dacb3a05e9adf1.png$

Figure $\PageIndex{8}$

Example $\PageIndex{4}$: Interactive: Linear independence of two vectors in $\mathbb{R}^2$

$clipboard_ed924e46c18748f2dd5216ce7766a98ce.png$

Figure $\PageIndex{9}$: Move the vector heads and the demo will tell you if they are linearly independent and show you their span.

Example $\PageIndex{5}$: Interactive: Linear dependence of three vectors in $\mathbb{R}^2$

$clipboard_e82ab35f48567771c0cc1e297d88cf91b.png$

Figure $\PageIndex{10}$: Move the vector heads and the demo will tell you that they are linearly dependent and show you their span.

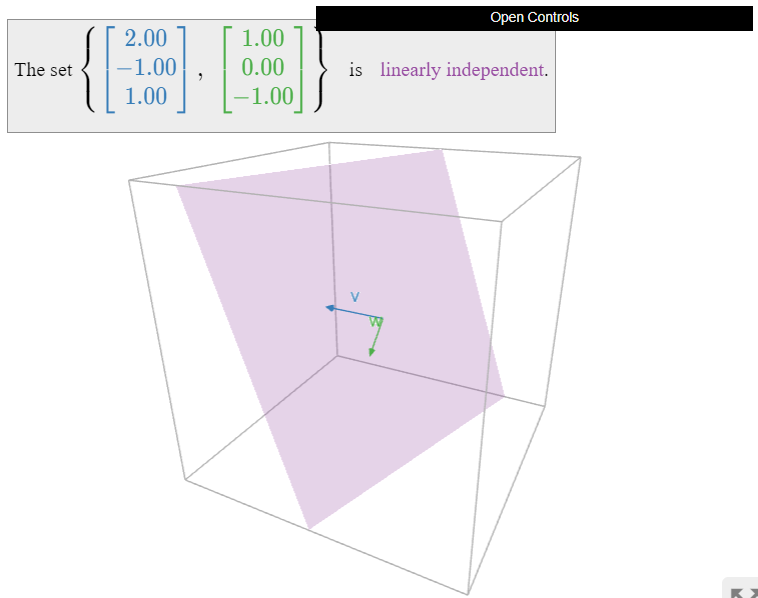
The two vectors $\{v,w\}$ below are linearly independent because they are not collinear.

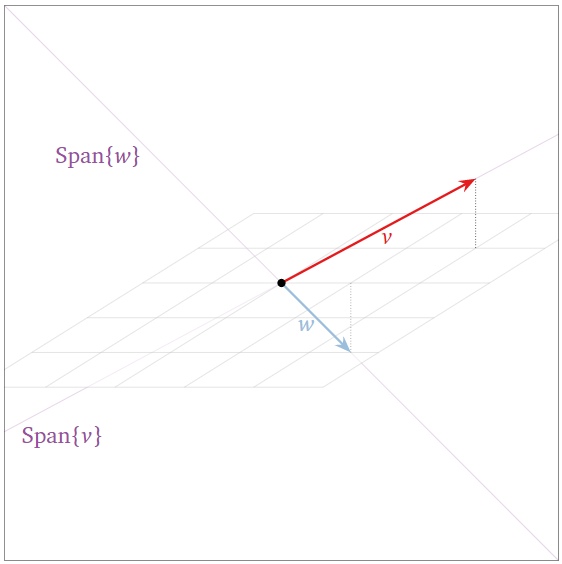
$clipboard_e055c6fcfbb197fbf5c2082cadd21e12a.png$

Figure $\PageIndex{11}$

The three vectors $\{v,w,u\}$ below are linearly independent: the span got bigger when we added $w\text{,}$ then again when we added $u\text{,}$ so we can apply the increasing span criterion, Theorem $\PageIndex{2}$.

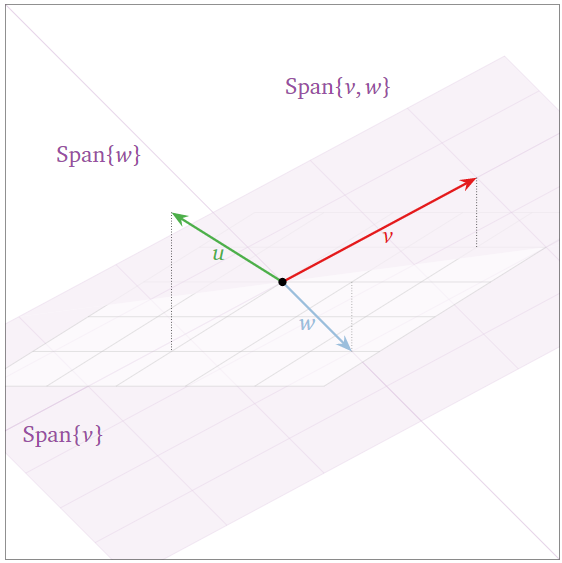
$clipboard_eeb7ea3785d2abbebcdce514479fe35f8.png$

Figure $\PageIndex{12}$

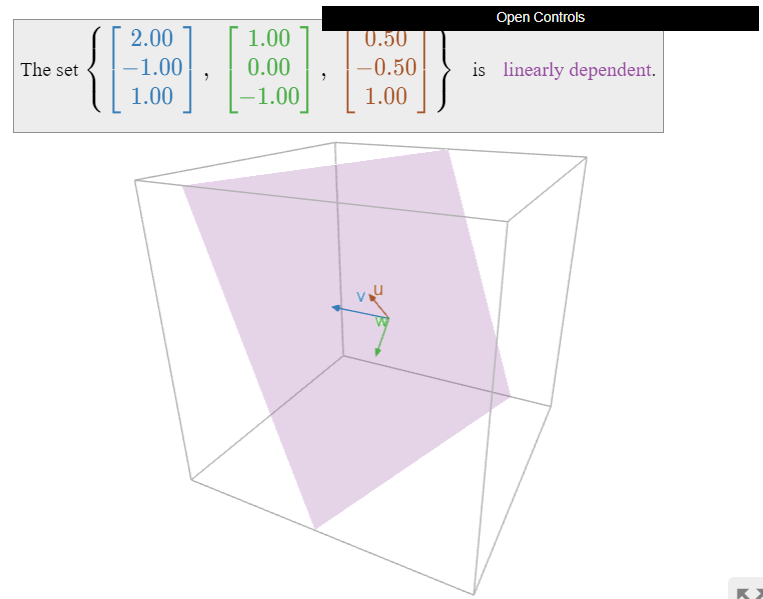
The three coplanar vectors $\{v,w,u\}$ below are linearly dependent:

$u$ is in $\text{Span}\{v,w\}\text{,}$ so we can apply the first criterion, Theorem $\PageIndex{1}$.
The span did not increase when we added $u\text{,}$ so we can apply the increasing span criterion, Theorem $\PageIndex{2}$.

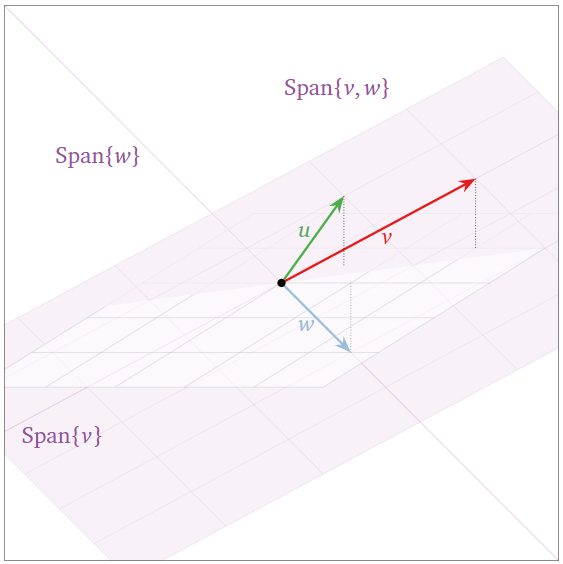
$clipboard_e1e565cf0afcfecfde0559e5235c621ac.png$

Figure $\PageIndex{13}$

Note that three vectors are linearly dependent if and only if they are coplanar. Indeed, $\{v,w,u\}$ is linearly dependent if and only if one vector is in the span of the other two, which is a plane (or a line) (or $\{0\}$).

The four vectors $\{v,w,u,x\}$ below are linearly dependent: they are the columns of a wide matrix, see Note $\PageIndex{2}$. Note however that $u$ is not contained in $\text{Span}\{v,w,x\}$. See this warning, Note $\PageIndex{3}$.

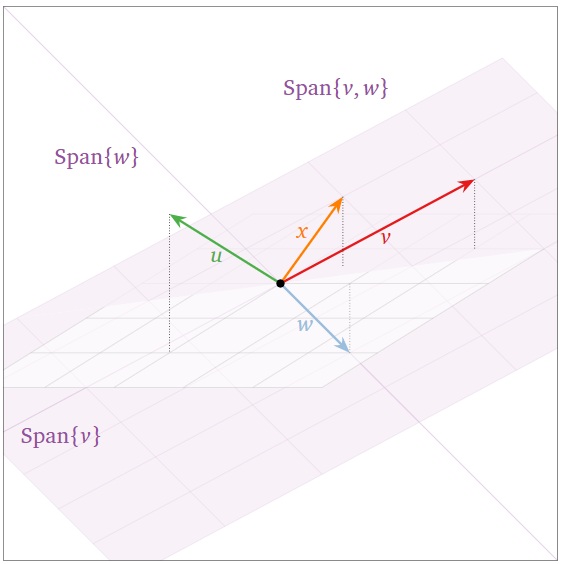
$clipboard_e75437f2ab2c039d7c4886bdec5e2650e.png$

Figure $\PageIndex{14}$: The vectors $\{v,w,u,x\}$ are linearly dependent, but $u$ is not contained in $\text{Span}\{v,w,x\}$.

Example $\PageIndex{6}$: Interactive: Linear independence of two vectors in $\mathbb{R}^3$

$clipboard_e10cd8efc73025353bab8a54ec51c4c83.png$

Figure $\PageIndex{15}$: Move the vector heads and the demo will tell you if they are linearly independent and show you their span.

Example $\PageIndex{7}$: Interactive: Linear independence of three vectors in $\mathbb{R}^3$

$clipboard_eebdeccfc15d71ca3f822c15f0213f1a1.png$

Figure $\PageIndex{16}$: Move the vector heads and the demo will tell you if they are linearly independent and show you their span.

Linear Dependence and Free Variables

In light of this important note, Recipe: Checking Linear Independence, and this criterion, Theorem $\PageIndex{1}$, it is natural to ask which columns of a matrix are redundant, i.e., which we can remove without affecting the column span.

Theorem $\PageIndex{3}$

Let $v_1,v_2,\ldots,v_k$ be vectors in $\mathbb{R}^n\text{,}$ and consider the matrix

\[A=\left(\begin{array}{cccc}|&|&\quad &| \\ v_1 &v_2 &\cdots &v_k \\ |&|&\quad &|\end{array}\right).\nonumber\]

Then we can delete the columns of $A$ without pivots (the columns corresponding to the free variables), without changing $\text{Span}\{v_1,v_2,\ldots,v_k\}$.

The pivot columns are linearly independent, so we cannot delete any more columns without changing the span.

Proof

If the matrix is in reduced row echelon form:

\[A=\left(\begin{array}{cccc}1&0&2&0 \\ 0&1&3&0 \\ 0&0&0&1\end{array}\right)\nonumber\]

then the column without a pivot is visibly in the span of the pivot columns:

\[\left(\begin{array}{c}2\\3\\0\end{array}\right)=2\left(\begin{array}{c}1\\0\\0\end{array}\right)+3\left(\begin{array}{c}0\\1\\0\end{array}\right)+0\left(\begin{array}{c}0\\0\\1\end{array}\right),\nonumber\]

and the pivot columns are linearly independent:

\[\left(\begin{array}{c}0\\0\\0\end{array}\right) =x_1\left(\begin{array}{c}1\\0\\0\end{array}\right)+x_2\left(\begin{array}{c}0\\1\\0\end{array}\right)+x_4\left(\begin{array}{c}0\\0\\1\end{array}\right)=\left(\begin{array}{c}x_1 \\x_2 \\ x_4\end{array}\right)\implies x_1 =x_2 =x_4 =0.\nonumber\]

If the matrix is not in reduced row echelon form, then we row reduce:

\[A=\left(\begin{array}{cccc}1&7&23&3 \\ 2&4&16&0 \\ -1&-2&-8&4\end{array}\right) \quad\xrightarrow{\text{RREF}}\quad \left(\begin{array}{cccc}1&0&2&0 \\ 0&1&3&0 \\ 0&0&0&1\end{array}\right).\nonumber\]

The following two vector equations have the same solution set, as they come from row-equivalent matrices:

\[\begin{aligned} x_1\left(\begin{array}{c}1\\2\\-1\end{array}\right)+x_2\left(\begin{array}{c}7\\4\\-2\end{array}\right)+x_3\left(\begin{array}{c}23\\16\\-8\end{array}\right)+x_4\left(\begin{array}{c}3\\0\\4\end{array}\right)&=0 \\ x_1\left(\begin{array}{c}1\\0\\0\end{array}\right)+x_2\left(\begin{array}{c}0\\1\\0\end{array}\right)+x_3\left(\begin{array}{c}2\\3\\0\end{array}\right)+x_4\left(\begin{array}{c}0\\0\\1\end{array}\right)&=0\end{aligned}\]

We conclude that

\[\left(\begin{array}{c}23\\16\\-8\end{array}\right)=2\left(\begin{array}{c}1\\2\\-1\end{array}\right)+3\left(\begin{array}{c}7\\4\\-2\end{array}\right)+0\left(\begin{array}{c}3\\0\\4\end{array}\right)\nonumber\]

and that

\[x_1\left(\begin{array}{c}1\\2\\-1\end{array}\right)+x_2\left(\begin{array}{c}7\\4\\-2\end{array}\right)+x_4\left(\begin{array}{c}3\\0\\4\end{array}\right)=0\nonumber\]

has only the trivial solution.

Note that it is necessary to row reduce $A$ to find which are its pivot columns, Definition 1.2.5 in Section 1.2. However, the span of the columns of the row reduced matrix is generally not equal to the span of the columns of $A\text{:}$ one must use the pivot columns of the original matrix. See theorem in Section 2.7, Theorem 2.7.2 for a restatement of the above theorem.

Example $\PageIndex{8}$

The matrix

\[A=\left(\begin{array}{cccc}1&2&0&-1 \\ -2&-3&4&5 \\ 2&4&0&-2\end{array}\right)\nonumber\]

has reduced row echelon form

\[\left(\begin{array}{cccc}1&0&-8&-7 \\ 0&1&4&3 \\ 0&0&0&0\end{array}\right).\nonumber\]

Therefore, the first two columns of $A$ are the pivot columns, so we can delete the others without changing the span:

\[\text{Span}\left\{\left(\begin{array}{c}1\\-2\\2\end{array}\right),\:\left(\begin{array}{c}2\\-3\\4\end{array}\right)\right\}=\text{Span}\left\{\left(\begin{array}{c}1\\-2\\2\end{array}\right),\:\left(\begin{array}{c}2\\-3\\4\end{array}\right),\:\left(\begin{array}{c}0\\4\\0\end{array}\right),\:\left(\begin{array}{c}-1\\5\\-2\end{array}\right)\right\}.\nonumber\]

Moreover, the first two columns are linearly independent.

Note $\PageIndex{5}$: Pivot Columns and Dimension

Let $d$ be the number of pivot columns in the matrix

\[A=\left(\begin{array}{cccc}|&|&\quad &| \\ v_1 &v_2 &\cdots &v_k \\ |&|&\quad &| \end{array}\right).\nonumber\]

If $d=1$ then $\text{Span}\{v_1,v_2,\ldots,v_k\}$ is a line.
If $d=2$ then $\text{Span}\{v_1,v_2,\ldots,v_k\}$ is a plane.
If $d=3$ then $\text{Span}\{v_1,v_2,\ldots,v_k\}$ is a 3-space.
Et cetera.

The number $d$ is called the dimension. We discussed this notion in this important note in Section 2.4, Note 2.4.4 and this important note in Section 2.4, Note 2.4.5. We will define this concept rigorously in Section 2.7.

Search

Definition \(\PageIndex{1}\): Linearly Independent and Linearly Dependent

Note: \(\PageIndex{1}\)

Example \(\PageIndex{1}\): Checking linear dependence

Solution

Example \(\PageIndex{2}\): Checking linear independence

Solution

Example \(\PageIndex{3}\): Vector parametric form

Recipe: Checking Linear Independence

Note \(\PageIndex{2}\)

Fact \(\PageIndex{1}\): Facts About Linear Independence

Theorem \(\PageIndex{1}\)

Note \(\PageIndex{3}\)

Theorem \(\PageIndex{2}\): Increasing Span Criterion

Note \(\PageIndex{4}\)

Example \(\PageIndex{4}\): Interactive: Linear independence of two vectors in \(\mathbb{R}^2\)

Example \(\PageIndex{5}\): Interactive: Linear dependence of three vectors in \(\mathbb{R}^2\)

Example \(\PageIndex{6}\): Interactive: Linear independence of two vectors in \(\mathbb{R}^3\)

Example \(\PageIndex{7}\): Interactive: Linear independence of three vectors in \(\mathbb{R}^3\)

Theorem \(\PageIndex{3}\)

Example \(\PageIndex{8}\)

Note \(\PageIndex{5}\): Pivot Columns and Dimension