2.7: Basis and Dimension

Last updated
Save as PDF

Page ID: 70192

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectives

Understand the definition of a basis of a subspace.
Understand the basis theorem.
Recipes: basis for a column space, basis for a null space, basis of a span.
Picture: basis of a subspace of $\mathbb{R}^2 $ or $\mathbb{R}^3 $.
Theorem: basis theorem.
Essential vocabulary words: basis, dimension.

Basis of a Subspace

As we discussed in Section 2.6, a subspace is the same as a span, except we do not have a set of spanning vectors in mind. There are infinitely many choices of spanning sets for a nonzero subspace; to avoid redundancy, usually it is most convenient to choose a spanning set with the minimal number of vectors in it. This is the idea behind the notion of a basis.

Definition $\PageIndex{1}$: Basis

Let $V$ be a subspace of $\mathbb{R}^n $. A basis of $V$ is a set of vectors $\{v_1,v_2,\ldots,v_m\}$ in $V$ such that:

$V = \text{Span}\{v_1,v_2,\ldots,v_m\}\text{,}$ and
the set $\{v_1,v_2,\ldots,v_m\}$ is linearly independent.

Recall that a set of vectors is linearly independent if and only if, when you remove any vector from the set, the span shrinks (Theorem 2.5.1 in Section 2.5). In other words, if $\{v_1,v_2,\ldots,v_m\}$ is a basis of a subspace $V\text{,}$ then no proper subset of $\{v_1,v_2,\ldots,v_m\}$ will span $V\text{:}$ it is a minimal spanning set. Any subspace admits a basis by Theorem 2.6.1 in Section 2.6.

Note $\PageIndex{1}$

A nonzero subspace has infinitely many different bases, but they all contain the same number of vectors.

We leave it as an exercise to prove that any two bases have the same number of vectors; one might want to wait until after learning the invertible matrix theorem in Section 3.5.

Definition $\PageIndex{2}$: Dimension

Let $V$ be a subspace of $\mathbb{R}^n $. The number of vectors in any basis of $V$ is called the dimension of $V\text{,}$ and is written $\dim V$.

Example $\PageIndex{1}$: A basis of $\mathbb{R}^2 $

Find a basis of $\mathbb{R}^2 $.

Solution

We need to find two vectors in $\mathbb{R}^2 $ that span $\mathbb{R}^2 $ and are linearly independent. One such basis is $\bigl\{{1\choose 0},{0\choose 1}\bigr\}\text{:}$

They span because any vector $a\choose b$ can be written as a linear combination of ${1\choose 0},{0\choose 1}\text{:}$
\[\left(\begin{array}{c}a\\b\end{array}\right)=a\left(\begin{array}{c}1\\0\end{array}\right)+b\left(\begin{array}{c}0\\1\end{array}\right).\nonumber\]
They are linearly independent: if
\[x\left(\begin{array}{c}1\\0\end{array}\right)+y\left(\begin{array}{c}0\\1\end{array}\right)=\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}0\\0\end{array}\right)\nonumber\]
then $x=y=0$.

This shows that the plane $\mathbb{R}^2 $ has dimension 2.

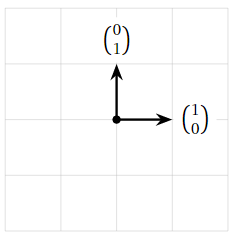
$clipboard_ef648f6cb9fbe0961161638fe96e98cf6.png$

Figure $\PageIndex{1}$

Example $\PageIndex{2}$: All bases of $\mathbb{R}^2 $

Find all bases of $\mathbb{R}^2 $.

Solution

We know from the previous Example $\PageIndex{1}$ that $\mathbb{R}^2 $ has dimension 2, so any basis of $\mathbb{R}^2 $ has two vectors in it. Let $v_1,v_2$ be vectors in $\mathbb{R}^2 \text{,}$ and let $A$ be the matrix with columns $v_1,v_2$.

To say that $\{v_1,v_2\}$ spans $\mathbb{R}^2 $ means that $A$ has a pivot, Definition 1.2.5 in Section 1.2, in every row: see Theorem 2.3.1 in Section 2.3.
To say that $\{v_1,v_2\}$ is linearly independent means that $A$ has a pivot in every column: see Recipe: Checking linear independence in Section 2.5.

Since $A$ is a $2\times 2$ matrix, it has a pivot in every row exactly when it has a pivot in every column. Hence any two noncollinear vectors form a basis of $\mathbb{R}^2 $. For example,

\[\left\{\left(\begin{array}{c}1\\0\end{array}\right),\:\left(\begin{array}{c}1\\1\end{array}\right)\right\}\nonumber\]

is a basis.

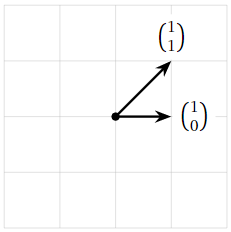
$clipboard_eaee98f686c47a50da0fc4ad4b595c82d.png$

Figure $\PageIndex{2}$

Example $\PageIndex{3}$: The standard basis of $\mathbb{R}^n $

One shows exactly as in the above Example $\PageIndex{1}$ that the standard coordinate vectors

\[e_1=\left(\begin{array}{c}1\\0\\ \vdots \\ 0\\0\end{array}\right),\quad e_2=\left(\begin{array}{c}0\\1\\ \vdots \\ 0\\0\end{array}\right),\quad\cdots ,\quad e_{n-1}=\left(\begin{array}{c}0\\0\\ \vdots \\1\\0\end{array}\right),\quad e_n=\left(\begin{array}{c}0\\0\\ \vdots \\0\\1\end{array}\right)\nonumber\]

form a basis for $\mathbb{R}^n $. This is sometimes known as the standard basis.

In particular, $\mathbb{R}^n $ has dimension $n$.

Example $\PageIndex{4}$

The previous Example $\PageIndex{3}$ implies that any basis for $\mathbb{R}^n $ has $n$ vectors in it. Let $v_1,v_2,\ldots,v_n$ be vectors in $\mathbb{R}^n \text{,}$ and let $A$ be the $n\times n$ matrix with columns $v_1,v_2,\ldots,v_n$.

To say that $\{v_1,v_2,\ldots,v_n\}$ spans $\mathbb{R}^n $ means that $A$ has a pivot position, Definition 1.2.5 in Section 1.2, in every row: see this Theorem 2.3.1 in Section 2.3.
To say that $\{v_1,v_2,\ldots,v_n\}$ is linearly independent means that $A$ has a pivot position in every column: see Recipe: Checking linear independence in Section 2.5.

Since $A$ is a square matrix, it has a pivot in every row if and only if it has a pivot in every column. We will see in Section 3.5 that the above two conditions are equivalent to the invertibility of the matrix $A$.

Example $\PageIndex{5}$

Let

\[V=\left\{\left(\begin{array}{c}x\\y\\z\end{array}\right)\text{ in }\mathbb{R}^{3}|x+3y+z=0\right\}\quad\mathcal{B}=\left\{\left(\begin{array}{c}-3\\1\\0\end{array}\right),\:\left(\begin{array}{c}0\\1\\-3\end{array}\right)\right\}.\nonumber\]

Verify that $V$ is a subspace, and show directly that $\mathcal{B}$ is a basis for $V$.

Solution

First we observe that $V$ is the solution set of the homogeneous equation $x + 3y + z = 0\text{,}$ so it is a subspace: see this note in Section 2.6, Note 2.6.3. To show that $\mathcal{B}$ is a basis, we really need to verify three things:

Both vectors are in $V$ because
\[\begin{array}{rrrrrrl} (-3) &+& 3(1) &+& (0) &=& 0\\ (0) &+& 3(1) &+& (-3) &=& 0.\end{array}\nonumber\]
Span: suppose that $\left(\begin{array}{c}x\\y\\z\end{array}\right)$ is in $V$. Since $x + 3y + z = 0$ we have $y = -\frac 13(x+z)\text{,}$ so
\[\left(\begin{array}{c}x\\y\\z\end{array}\right)=\left(\begin{array}{c}x\\ {-\frac{1}{3}(x+z)} \\ z\end{array}\right)=-\frac{x}{3}\left(\begin{array}{c}-3\\1\\0\end{array}\right)-\frac{z}{3}\left(\begin{array}{c}0\\1\\-3\end{array}\right).\nonumber\]
Hence $\mathcal{B}$ spans $V$.
Linearly independent:
\[c_1\left(\begin{array}{c}-3\\1\\0\end{array}\right)+c_2\left(\begin{array}{c}0\\1\\-3\end{array}\right)=0\implies\left(\begin{array}{c}-3c_1 \\ c_1+c_2 \\ -3c_2\end{array}\right)=\left(\begin{array}{c}0\\0\\0\end{array}\right)\implies c_1=c_2=0.\nonumber\]
Alternatively, one can observe that the two vectors are not collinear.

Since $V$ has a basis with two vectors, it has dimension two: it is a plane.

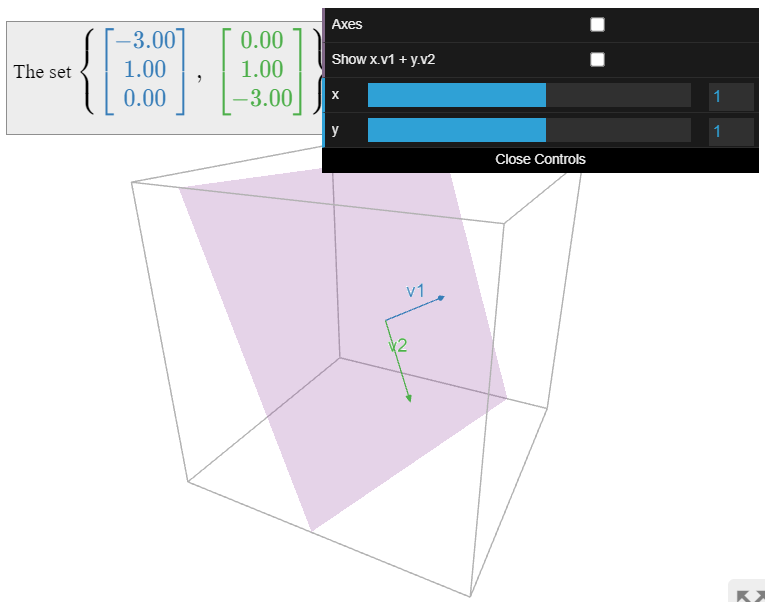
$clipboard_e3a38b437bd7307a882c23cd090e0d6a5.png$

Figure $\PageIndex{3}$: A picture of the plane $V$ and its basis $\mathcal{B} = \{v_1,v_2\}$. Note that $\mathcal{B}$ spans $V$ and is linearly independent.

This example is somewhat contrived, in that we will learn systematic methods for verifying that a subset is a basis. The intention is to illustrate the defining properties of a basis.

Computing a Basis for a Subspace

Now we show how to find bases for the column space of a matrix and the null space of a matrix. In order to find a basis for a given subspace, it is usually best to rewrite the subspace as a column space or a null space first: see this note in Section 2.6, Note 2.6.3

A Basis for the Column Space

First we show how to compute a basis for the column space of a matrix.

Theorem $\PageIndex{1}$

The pivot columns of a matrix $A$ form a basis for $\text{Col}(A)$.

Proof: This is a restatement of Theorem 2.5.3 in Section 2.5.

Note $\PageIndex{2}$

The above theorem is referring to the pivot columns in the original matrix, not its reduced row echelon form. Indeed, a matrix and its reduced row echelon form generally have different column spaces. For example, in the matrix $A$ below:

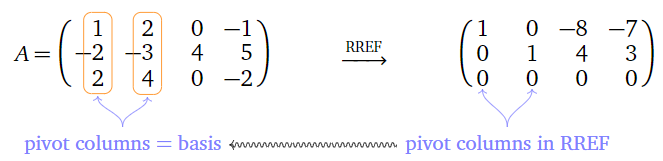
$clipboard_e30df1603622fd0c9c8d44b8b7acbf773.png$

Figure $\PageIndex{4}$

the pivot columns are the first two columns, so a basis for $\text{Col}(A)$ is

\[\left\{\left(\begin{array}{c}1\\-2\\2\end{array}\right),\:\left(\begin{array}{c}2\\-3\\4\end{array}\right)\right\}.\nonumber\]

The first two columns of the reduced row echelon form certainly span a different subspace, as

\[\text{Span}\left\{\left(\begin{array}{c}1\\0\\0\end{array}\right),\:\left(\begin{array}{c}0\\1\\0\end{array}\right)\right\}=\left\{\left(\begin{array}{c}a\\b\\0\end{array}\right)|a,b\text{ in }\mathbb{R}\right\}=(x,y\text{-plane}),\nonumber\]

but $\text{Col}(A)$ contains vectors whose last coordinate is nonzero.

Corollary $\PageIndex{1}$

The dimension of $\text{Col}(A)$ is the number of pivots of $A$.

A Basis of a Span

Computing a basis for a span is the same as computing a basis for a column space. Indeed, the span of finitely many vectors $v_1,v_2,\ldots,v_m$ is the column space of a matrix, namely, the matrix $A$ whose columns are $v_1,v_2,\ldots,v_m\text{:}$

\[A=\left(\begin{array}{cccc}|&|&\quad &| \\ v_1 &v_2 &\cdots &v_m \\ |&|&\quad &|\end{array}\right).\nonumber\]

Example $\PageIndex{6}$: A basis of a span

Find a basis of the subspace

\[V=\text{Span}\left\{\left(\begin{array}{c}1\\-2\\2\end{array}\right),\:\left(\begin{array}{c}2\\-3\\4\end{array}\right),\:\left(\begin{array}{c}0\\4\\0\end{array}\right),\:\left(\begin{array}{c}-1\\5\\-2\end{array}\right)\right\}.\nonumber\]

Solution

The subspace $V$ is the column space of the matrix

\[A=\left(\begin{array}{cccc}1&2&0&-1 \\ -2&-3&4&5 \\ 2&4&0&-2\end{array}\right).\nonumber\]

The reduced row echelon form of this matrix is

\[\left(\begin{array}{cccc}1&0&-8&-7 \\ 0&1&4&3 \\ 0&0&0&0\end{array}\right).\nonumber\]

The first two columns are pivot columns, so a basis for $V$ is

\[\left\{\left(\begin{array}{c}1\\-2\\2\end{array}\right),\:\left(\begin{array}{c}2\\-3\\4\end{array}\right)\right\}.\nonumber\]

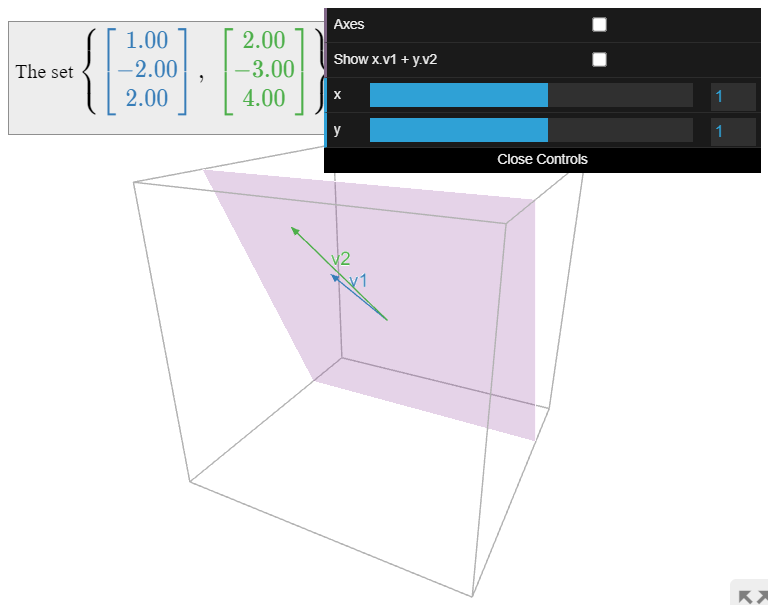
$clipboard_e4d07f10b1cd0f85aeac3bd4b7783e99b.png$

Figure $\PageIndex{5}$: A picture of the plane $V$ and its basis $\mathcal{B} = \{v_1,v_2\}$.

Example $\PageIndex{7}$: Another basis of the same span

Find a basis of the subspace

which does not consist of the first two vectors, as in the previous Example $\PageIndex{6}$.

Solution

The point of this example is that the above Theorem $\PageIndex{1}$ gives one basis for $V\text{;}$ as always, there are infinitely more.

Reordering the vectors, we can express $V$ as the column space of

\[A'=\left(\begin{array}{cccc}0&-1&1&2 \\ 4&5&-2&-3 \\ 0&-2&2&4\end{array}\right).\nonumber\]

The reduced row echelon form of this matrix is

\[\left(\begin{array}{cccc}1&0&3/4 &7/4 \\ 0&1&-1&-2 \\ 0&0&0&0\end{array}\right).\nonumber\]

The first two columns are pivot columns, so a basis for $V$ is

\[\left\{\left(\begin{array}{c}0\\4\\0\end{array}\right),\:\left(\begin{array}{c}-1\\5\\-2\end{array}\right)\right\}.\nonumber\]

These are the last two vectors in the given spanning set.

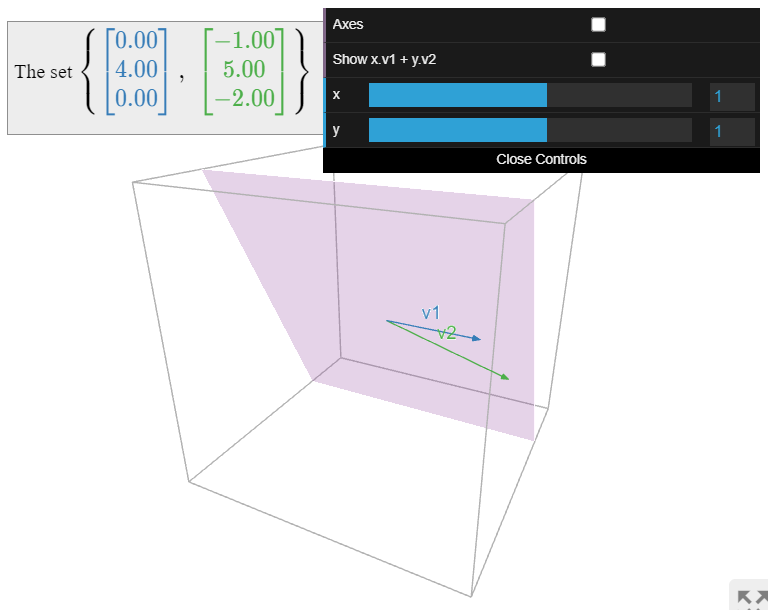
$clipboard_e4e2c376b37b58525fe4fbcc547a4f0ed.png$

Figure $\PageIndex{6}$: A picture of the plane $V$ and its basis $\mathcal{B} = \{v_1,v_2\}$.

A Basis for the Null Space

In order to compute a basis for the null space of a matrix, one has to find the parametric vector form of the solutions of the homogeneous equation $Ax=0$.

Theorem $\PageIndex{2}$

The vectors attached to the free variables in the parametric vector form of the solution set of $Ax=0$ form a basis of $\text{Nul}(A)$.

The proof of the theorem has two parts. The first part is that every solution lies in the span of the given vectors. This is automatic: the vectors are exactly chosen so that every solution is a linear combination of those vectors. The second part is that the vectors are linearly independent. This part was discussed in Example 2.5.3 in Section 2.5.

A Basis for a General Subspace

As mentioned at the beginning of this subsection, when given a subspace written in a different form, in order to compute a basis it is usually best to rewrite it as a column space or null space of a matrix.

Example $\PageIndex{8}$: A basis of a subspace

Let $V$ be the subspace defined by

\[V=\left\{\left(\begin{array}{c}x\\y\\z\end{array}\right)|x+2y=z\right\}.\nonumber\]

Find a basis for $V$. What is $\dim(V)\text{?}$

Solution

First we notice that $V$ is exactly the solution set of the homogeneous linear equation $x + 2y - z = 0$. Hence $V = \text{Nul}\left(\begin{array}{ccc}1&2&-1\end{array}\right).$ This matrix is in reduced row echelon form; the parametric form of the general solution is $x = -2y + z\text{,}$ so the parametric vector form is

\[\left(\begin{array}{c}x\\y\\z\end{array}\right)=y\left(\begin{array}{c}-2\\1\\0\end{array}\right)=z\left(\begin{array}{c}1\\0\\1\end{array}\right).\nonumber\]

It follows that a basis is

\[\left\{\left(\begin{array}{c}-2\\1\\0\end{array}\right),\:\left(\begin{array}{c}1\\0\\1\end{array}\right)\right\}.\nonumber\]

Since $V$ has a basis with two vectors, its dimension is $2\text{:}$ it is a plane.

The Basis Theorem

Recall that $\{v_1,v_2,\ldots,v_n\}$ forms a basis for $\mathbb{R}^n $ if and only if the matrix $A$ with columns $v_1,v_2,\ldots,v_n$ has a pivot in every row and column (see this Example $\PageIndex{4}$). Since $A$ is an $n\times n$ matrix, these two conditions are equivalent: the vectors span if and only if they are linearly independent. The basis theorem is an abstract version of the preceding statement, that applies to any subspace.

Theorem $\PageIndex{3}$: Basis Theorem

Let $V$ be a subspace of dimension $m$. Then:

Any $m$ linearly independent vectors in $V$ form a basis for $V$.
Any $m$ vectors that span $V$ form a basis for $V$.

Proof

Suppose that $\mathcal{B} = \{v_1,v_2,\ldots,v_m\}$ is a set of linearly independent vectors in $V$. In order to show that $\mathcal{B}$ is a basis for $V\text{,}$ we must prove that $V = \text{Span}\{v_1,v_2,\ldots,v_m\}.$ If not, then there exists some vector $v_{m+1}$ in $V$ that is not contained in $\text{Span}\{v_1,v_2,\ldots,v_m\}.$ By the increasing span criterion Theorem 2.5.2 in Section 2.5, the set $\{v_1,v_2,\ldots,v_m,v_{m+1}\}$ is also linearly independent. Continuing in this way, we keep choosing vectors until we eventually do have a linearly independent spanning set: say $V = \text{Span}\{v_1,v_2,\ldots,v_m,\ldots,v_{m+k}\}$. Then $\{v_1,v_2,\ldots,v_{m+k}\}$ is a basis for $V\text{,}$ which implies that $\dim(V) = m+k > m$. But we were assuming that $V$ has dimension $m\text{,}$ so $\mathcal{B}$ must have already been a basis.

Now suppose that $\mathcal{B} = \{v_1,v_2,\ldots,v_m\}$ spans $V$. If $\mathcal{B}$ is not linearly independent, then by this Theorem 2.5.1 in Section 2.5, we can remove some number of vectors from $\mathcal{B}$ without shrinking its span. After reordering, we can assume that we removed the last $k$ vectors without shrinking the span, and that we cannot remove any more. Now $V = \text{Span}\{v_1,v_2,\ldots,v_{m-k}\}\text{,}$ and $\{v_1,v_2,\ldots,v_{m-k}\}$ is a basis for $V$ because it is linearly independent. This implies that $\dim V=m-k < m$. But we were assuming that $\dim V = m\text{,}$ so $\mathcal{B}$ must have already been a basis.

In other words, if you already know that $\dim V = m\text{,}$ and if you have a set of $m$ vectors $\mathcal{B} = \{v_1,v_2,\ldots,v_m\}$ in $V\text{,}$ then you only have to check one of:

$\mathcal{B}$ is linearly independent, or
$\mathcal{B}$ spans $V\text{,}$

in order for $\mathcal{B}$ to be a basis of $V$. If you did not already know that $\dim V = m\text{,}$ then you would have to check both properties.

To put it yet another way, suppose we have a set of vectors $\mathcal{B} = \{v_1,v_2,\ldots,v_m\}$ in a subspace $V$. Then if any two of the following statements is true, the third must also be true:

$\mathcal{B}$ is linearly independent,
$\mathcal{B}$ spans $V\text{,}$ and
$\dim V = m.$

For example, if $V$ is a plane, then any two noncollinear vectors in $V$ form a basis.

Example $\PageIndex{9}$: Two noncollinear vectors form a basis of a plane

Find a basis of the subspace

which is different from the bases in this Example $\PageIndex{6}$ and this Example $\PageIndex{7}$.

Solution

We know from the previous examples that $\dim V = 2$. By the Theorem $\PageIndex{3}$, it suffices to find any two noncollinear vectors in $V$. We write two linear combinations of the four given spanning vectors, chosen at random:

\[w_1=\left(\begin{array}{c}1\\-2\\2\end{array}\right)+\left(\begin{array}{c}2\\-3\\4\end{array}\right)=\left(\begin{array}{c}3\\-5\\6\end{array}\right)\quad w_2=-\left(\begin{array}{c}2\\-3\\4\end{array}\right)+\frac{1}{2}\left(\begin{array}{c}0\\4\\0\end{array}\right)=\left(\begin{array}{c}-2\\5\\-4\end{array}\right).\nonumber\]

Since $w_1,w_2$ are not collinear, $\mathcal{B} = \{w_1,w_2\}$ is a basis for $V$.

$clipboard_e6d6a6eeeaaff43e2a003f5455fe70c4d.png$

Figure $\PageIndex{7}$: A picture of the plane $V$ and its basis $\mathcal{B} = \{w_1,w_2\}$.

Example $\PageIndex{10}$: Finding a basis by inspection

Find a basis for the plane

\[V=\left\{\left(\begin{array}{c}x_1\\x_2\\x_3\end{array}\right)|x_1 +x_2=x_3\right\}\nonumber\]

by inspection. (This plane is expressed in set builder notation, Note 2.2.3 in Section 2.2.)

Solution

First note that $V$ is the null space of the matrix $\left(\begin{array}{ccc}1&1&-1\end{array}\right)$ this matrix is in reduced row echelon form and has two free variables, so $V$ is indeed a plane. We write down two vectors satisfying $x_1 + x_2 = x_3\text{:}$

\[v_1=\left(\begin{array}{c}1\\0\\1\end{array}\right)\quad v_2=\left(\begin{array}{c}0\\1\\1\end{array}\right).\nonumber\]

Since $v_1$ and $v_2$ are not collinear, they are linearly independent; since $\dim(V) = 2\text{,}$ the basis theorem implies that $\{v_1,v_2\}$ is a basis for $V$.

Search

Definition \(\PageIndex{1}\): Basis

Note \(\PageIndex{1}\)

Definition \(\PageIndex{2}\): Dimension

Example \(\PageIndex{1}\): A basis of \(\mathbb{R}^2 \)

Solution

Example \(\PageIndex{2}\): All bases of \(\mathbb{R}^2 \)

Solution

Example \(\PageIndex{3}\): The standard basis of \(\mathbb{R}^n \)

Example \(\PageIndex{4}\)

Example \(\PageIndex{5}\)

Solution

Theorem \(\PageIndex{1}\)

Note \(\PageIndex{2}\)

Corollary \(\PageIndex{1}\)

Example \(\PageIndex{6}\): A basis of a span

Solution

Example \(\PageIndex{7}\): Another basis of the same span

Solution

Theorem \(\PageIndex{2}\)

Example \(\PageIndex{8}\): A basis of a subspace

Solution

Theorem \(\PageIndex{3}\): Basis Theorem

Example \(\PageIndex{9}\): Two noncollinear vectors form a basis of a plane

Solution

Example \(\PageIndex{10}\): Finding a basis by inspection

Solution