4.2: Cofactor Expansions
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Learn to recognize which methods are best suited to compute the determinant of a given matrix.
- Recipes: the determinant of a 3×3 matrix, compute the determinant using cofactor expansions.
- Vocabulary words: minor, cofactor.
In this section, we give a recursive formula for the determinant of a matrix, called a cofactor expansion. The formula is recursive in that we will compute the determinant of an n×n matrix assuming we already know how to compute the determinant of an (n−1)×(n−1) matrix.
At the end is a supplementary subsection on Cramer’s rule and a cofactor formula for the inverse of a matrix.
Cofactor Expansions
A recursive formula must have a starting point. For cofactor expansions, the starting point is the case of 1×1 matrices. The definition of determinant directly implies that
det(a)=a.
To describe cofactor expansions, we need to introduce some notation.
Let A be an n×n matrix.
- The (i,j) minor, denoted Aij, is the (n−1)×(n−1) matrix obtained from A by deleting the ith row and the jth column.
- The (i,j) cofactor Cij is defined in terms of the minor by Cij=(−1)i+jdet(Aij).
Note that the signs of the cofactors follow a “checkerboard pattern.” Namely, (−1)i+j is pictured in this matrix:
(+−+−−+−−+−+−−+−+).
For
A=(123456789),
compute A23 and C23.
Solution
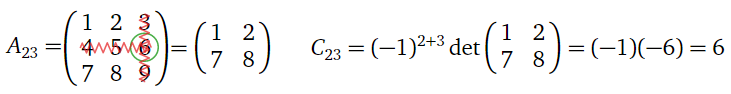
Figure 4.2.1
The cofactors Cij of an n×n matrix are determinants of (n−1)×(n−1) submatrices. Hence the following theorem is in fact a recursive procedure for computing the determinant.
Let A be an n×n matrix with entries aij.
- For any i=1,2,…,n, we have det(A)=n∑j=1aijCij=ai1Ci1+ai2Ci2+⋯+ainCin. This is called cofactor expansion along the ith row.
- For any j=1,2,…,n, we have det(A)=n∑i=1aijCij=a1jC1j+a2jC2j+⋯+anjCnj. This is called cofactor expansion along the jth column.
- Proof
-
First we will prove that cofactor expansion along the first column computes the determinant. Define a function d:{n×n matrices}→R by
d(A)=n∑i=1(−1)i+1ai1det(Ai1).
We want to show that d(A)=det(A). Instead of showing that d satisfies the four defining properties of the determinant, Definition 4.1.1, in Section 4.1, we will prove that it satisfies the three alternative defining properties, Remark: Alternative defining properties, in Section 4.1, which were shown to be equivalent.
- We claim that d is multilinear in the rows of A. Let A be the matrix with rows v1,v2,…,vi−1,v+w,vi+1,…,vn: A=(a11a12a13b1+c1b2+c2b3+c3a31a32a33). Here we let bi and ci be the entries of v and w, respectively. Let B and C be the matrices with rows v1,v2,…,vi−1,v,vi+1,…,vn and v1,v2,…,vi−1,w,vi+1,…,vn, respectively: B=(a11a12a13b1b2b3a31a32a33)C=(a11a12a13c1c2c3a31a32a33). We wish to show d(A)=d(B)+d(C). For i′≠i, the (i′,1)-cofactor of A is the sum of the (i′,1)-cofactors of B and C, by multilinearity of the determinants of (n−1)×(n−1) matrices: (−1)3+1det(A31)=(−1)3+1det(a12a13b2+c2b3+c3)=(−1)3+1det(a12a13b2b3)+(−1)3+1det(a12a13c2c3)=(−1)3+1det(B31)+(−1)3+1det(C31). On the other hand, the (i,1)-cofactors of A,B, and C are all the same: (−1)2+1det(A21)=(−1)2+1det(a12a13a32a33)=(−1)2+1det(B21)=(−1)2+1det(C21). Now we compute d(A)=(−1)i+1(bi+ci)det(Ai1)+∑i′≠i(−1)i′+1ai1det(Ai′1)=(−1)i+1bidet(Bi1)+(−1)i+1cidet(Ci1)+∑i′≠i(−1)i′+1ai1(det(Bi′1)+det(Ci′1))=[(−1)i+1bidet(Bi1)+∑i′≠i(−1)i′+1ai1det(Bi′1)]+[(−1)i+1cidet(Ci1)+∑i′≠i(−1)i′+1ai1det(Ci′1)]=d(B)+d(C), as desired. This shows that d(A) satisfies the first defining property in the rows of A.
We still have to show that d(A) satisfies the second defining property in the rows of A. Let B be the matrix obtained by scaling the ith row of A by a factor of c:
A=(a11a12a13a21a22a23a31a32a33)B=(a11a12a13ca21ca22ca23a31a32a33). We wish to show that d(B)=cd(A). For i′≠i, the (i′,1)-cofactor of B is c times the (i′,1)-cofactor of A, by multilinearity of the determinants of (n−1)×(n−1)-matrices: (−1)3+1det(B31)=(−1)3+1det(a12a13ca22ca23)=(−1)3+1⋅cdet(a12a13a22a23)=(−1)3+1⋅cdet(A31). On the other hand, the (i,1)-cofactors of A and B are the same: (−1)2+1det(B21)=(−1)2+1det(a12a13a32a33)=(−1)2+1det(A21). Now we compute d(B)=(−1)i+1cai1det(Bi1)+∑i′≠i(−1)i′+1ai′1det(Bi′1)=(−1)i+1cai1det(Ai1)+∑i′≠i(−1)i′+1ai′1⋅cdet(Ai′1)=c[(−1)i+1cai1det(Ai1)+∑i′≠i(−1)i′+1ai′1det(Ai′1)]=cd(A), as desired. This completes the proof that d(A) is multilinear in the rows of A. - Now we show that d(A)=0 if A has two identical rows. Suppose that rows i1,i2 of A are identical, with i1<i2: A=(a11a12a13a14a21a22a23a24a31a32a33a34a11a12a13a14). If i≠i1,i2 then the (i,1)-cofactor of A is equal to zero, since Ai1 is an (n−1)×(n−1) matrix with identical rows: (−1)2+1det(A21)=(−1)2+1det(a12a13a14a32a33a34a12a13a14)=0. The (i1,1)-minor can be transformed into the (i2,1)-minor using i2−i1−1 row swaps:
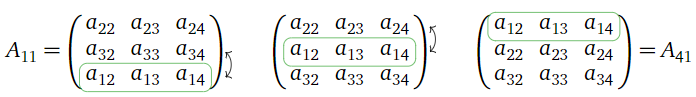
Figure 4.2.2
- Therefore, (−1)i1+1det(Ai11)=(−1)i1+1⋅(−1)i2−i1−1det(Ai21)=−(−1)i2+1det(Ai21). The two remaining cofactors cancel out, so d(A)=0, as desired.
- It remains to show that d(In)=1. The first is the only one nonzero term in the cofactor expansion of the identity: d(In)=1⋅(−1)1+1det(In−1)=1.
This proves that det(A)=d(A), i.e., that cofactor expansion along the first column computes the determinant.
Now we show that cofactor expansion along the jth column also computes the determinant. By performing j−1 column swaps, one can move the jth column of a matrix to the first column, keeping the other columns in order. For example, here we move the third column to the first, using two column swaps:

Figure 4.2.3
Let B be the matrix obtained by moving the jth column of A to the first column in this way. Then the (i,j) minor Aij is equal to the (i,1) minor Bi1, since deleting the ith column of A is the same as deleting the first column of B. By construction, the (i,j)-entry aij of A is equal to the (i,1)-entry bi1 of B. Since we know that we can compute determinants by expanding along the first column, we have
det(B)=n∑i=1(−1)i+1bi1det(Bi1)=n∑i=1(−1)i+1aijdet(Aij).
Since B was obtained from A by performing j−1 column swaps, we have
det(A)=(−1)j−1det(B)=(−1)j−1n∑i=1(−1)i+1aijdet(Aij)=n∑i=1(−1)i+jaijdet(Aij).
This proves that cofactor expansion along the ith column computes the determinant of A.
By the transpose property, Proposition 4.1.4 in Section 4.1, the cofactor expansion along the ith row of A is the same as the cofactor expansion along the ith column of AT. Again by the transpose property, we have det(A)=det(AT), so expanding cofactors along a row also computes the determinant.
- We claim that d is multilinear in the rows of A. Let A be the matrix with rows v1,v2,…,vi−1,v+w,vi+1,…,vn: A=(a11a12a13b1+c1b2+c2b3+c3a31a32a33). Here we let bi and ci be the entries of v and w, respectively. Let B and C be the matrices with rows v1,v2,…,vi−1,v,vi+1,…,vn and v1,v2,…,vi−1,w,vi+1,…,vn, respectively: B=(a11a12a13b1b2b3a31a32a33)C=(a11a12a13c1c2c3a31a32a33). We wish to show d(A)=d(B)+d(C). For i′≠i, the (i′,1)-cofactor of A is the sum of the (i′,1)-cofactors of B and C, by multilinearity of the determinants of (n−1)×(n−1) matrices: (−1)3+1det(A31)=(−1)3+1det(a12a13b2+c2b3+c3)=(−1)3+1det(a12a13b2b3)+(−1)3+1det(a12a13c2c3)=(−1)3+1det(B31)+(−1)3+1det(C31). On the other hand, the (i,1)-cofactors of A,B, and C are all the same: (−1)2+1det(A21)=(−1)2+1det(a12a13a32a33)=(−1)2+1det(B21)=(−1)2+1det(C21). Now we compute d(A)=(−1)i+1(bi+ci)det(Ai1)+∑i′≠i(−1)i′+1ai1det(Ai′1)=(−1)i+1bidet(Bi1)+(−1)i+1cidet(Ci1)+∑i′≠i(−1)i′+1ai1(det(Bi′1)+det(Ci′1))=[(−1)i+1bidet(Bi1)+∑i′≠i(−1)i′+1ai1det(Bi′1)]+[(−1)i+1cidet(Ci1)+∑i′≠i(−1)i′+1ai1det(Ci′1)]=d(B)+d(C), as desired. This shows that d(A) satisfies the first defining property in the rows of A.
Note that the theorem actually gives 2n different formulas for the determinant: one for each row and one for each column. For instance, the formula for cofactor expansion along the first column is
det(A)=n∑i=1ai1Ci1=a11C11+a21C21+⋯+an1Cn1=a11det(A11)−a21det(A21)+a31det(A31)−⋯±an1det(An1).
Remember, the determinant of a matrix is just a number, defined by the four defining properties, Definition 4.1.1 in Section 4.1, so to be clear:
You obtain the same number by expanding cofactors along any row or column.
Now that we have a recursive formula for the determinant, we can finally prove the existence theorem, Theorem 4.1.1 in Section 4.1.
Let us review what we actually proved in Section 4.1. We showed that if det:{n×n matrices}→R is any function satisfying the four defining properties of the determinant, Definition 4.1.1 in Section 4.1, (or the three alternative defining properties, Remark: Alternative defining properties,), then it also satisfies all of the wonderful properties proved in that section. In particular, since det can be computed using row reduction by Recipe: Computing Determinants by Row Reducing, it is uniquely characterized by the defining properties. What we did not prove was the existence of such a function, since we did not know that two different row reduction procedures would always compute the same answer.
Consider the function d defined by cofactor expansion along the first row:
d(A)=n∑i=1(−1)i+1ai1det(Ai1).
If we assume that the determinant exists for (n−1)×(n−1) matrices, then there is no question that the function d exists, since we gave a formula for it. Moreover, we showed in the proof of Theorem 4.2.1 above that d satisfies the three alternative defining properties of the determinant, again only assuming that the determinant exists for (n−1)×(n−1) matrices. This proves the existence of the determinant for n×n matrices!
This is an example of a proof by mathematical induction. We start by noticing that det(a)=a satisfies the four defining properties of the determinant of a 1×1 matrix. Then we showed that the determinant of n×n matrices exists, assuming the determinant of (n−1)×(n−1) matrices exists. This implies that all determinants exist, by the following chain of logic:
1×1 exists⟹2×2 exists⟹3×3 exists⟹⋯.
Find the determinant of
A=(213−121−223).
Solution
We make the somewhat arbitrary choice to expand along the first row. The minors and cofactors are
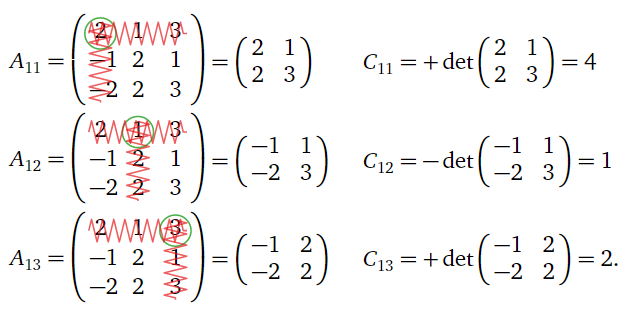
Figure 4.2.4
Thus,
det(A)=a11C11+a12C12+a13C13=(2)(4)+(1)(1)+(3)(2)=15.
Let us compute (again) the determinant of a general 2×2 matrix
A=(abcd).
The minors are
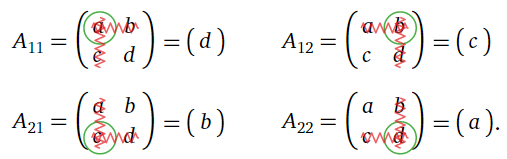
Figure 4.2.5
The minors are all 1×1 matrices. As we have seen that the determinant of a 1×1 matrix is just the number inside of it, the cofactors are therefore
C11=+det(A11)=dC12=−det(A12)=−cC21=−det(A21)=−bC22=+det(A22)=a
Expanding cofactors along the first column, we find that
det(A)=aC11+cC21=ad−bc,
which agrees with the formulas in Definition 3.5.2 in Section 3.5 and Example 4.1.6 in Section 4.1.
We can also use cofactor expansions to find a formula for the determinant of a 3×3 matrix. Let is compute the determinant of
A=(a11a12a13a21a22a23a31a32a33)
by expanding along the first row. The minors and cofactors are:
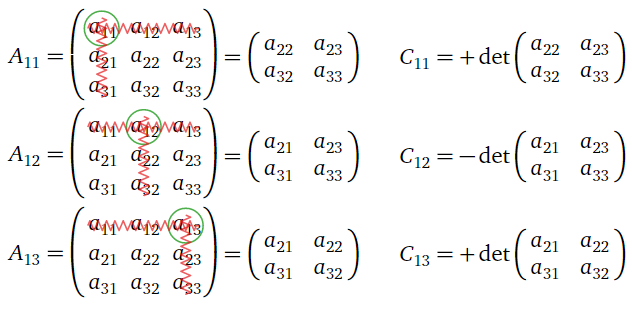
Figure 4.2.6
The determinant is:
det(A)=a11C11+a12C12+a13C13=a11det(a22a23a32a33)−a12det(a21a23a31a33)+a13det(a21a22a31a32)=a11(a22a33−a23a32)−a12(a21a33−a23a31)+a13(a21a32−a22a31)=a11a22a33+a12a23a31+a13a21a32−a13a22a31−a11a23a32−a12a21a33.
The formula for the determinant of a 3×3 matrix looks too complicated to memorize outright. Fortunately, there is the following mnemonic device.
To compute the determinant of a 3×3 matrix, first draw a larger matrix with the first two columns repeated on the right. Then add the products of the downward diagonals together, and subtract the products of the upward diagonals:
det(a11a12a13a21a22a23a31a32a33)=a11a22a33+a12a23a31+a13a21a32−a13a22a31−a11a23a32−a12a21a33
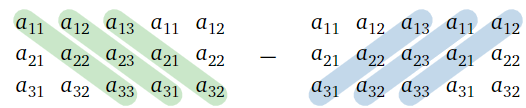
Figure 4.2.7
Alternatively, it is not necessary to repeat the first two columns if you allow your diagonals to “wrap around” the sides of a matrix, like in Pac-Man or Asteroids.
Find the determinant of A=(13520−14−31).
Solution
We repeat the first two columns on the right, then add the products of the downward diagonals and subtract the products of the upward diagonals:
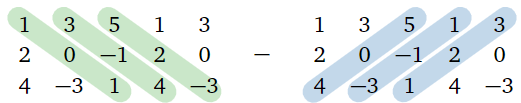
Figure 4.2.8
det(13520−14−31)=(1)(0)(1)+(3)(−1)(4)+(5)(2)(−3)−(5)(0)(4)−(1)(−1)(−3)−(3)(2)(1)=−51.
Cofactor expansions are most useful when computing the determinant of a matrix that has a row or column with several zero entries. Indeed, if the (i,j) entry of A is zero, then there is no reason to compute the (i,j) cofactor. In the following example we compute the determinant of a matrix with two zeros in the fourth column by expanding cofactors along the fourth column.
Find the determinant of
A=(25−3−2−2−32−513−20−1640).
Solution
The fourth column has two zero entries. We expand along the fourth column to find
det(A)=2det(−2−3213−2−164)−5det(25−313−2−164)−0det(don't care)+0det(don't care).
We only have to compute two cofactors. We can find these determinants using any method we wish; for the sake of illustration, we will expand cofactors on one and use the formula for the 3×3 determinant on the other.
Expanding along the first column, we compute
det(−2−3213−2−164)=−2det(3−264)−det(−3264)−det(−323−2)=−2(24)−(−24)−0=−48+24+0=−24.
Using the formula for the 3×3 determinant, we have
det(25−313−2−164)=(2)(3)(4)+(5)(−2)(−1)+(−3)(1)(6)−(2)(−2)(6)−(5)(1)(4)−(−3)(3)(−1)=11.
Thus, we find that
det(A)=2(−24)−5(11)=−103.
Cofactor expansions are also very useful when computing the determinant of a matrix with unknown entries. Indeed, it is inconvenient to row reduce in this case, because one cannot be sure whether an entry containing an unknown is a pivot or not.
Compute the determinant of this matrix containing the unknown λ:
A=(−λ271231−λ2−401−λ70002−λ).
Solution
First we expand cofactors along the fourth row:
det(A)=0det(⋯)+0det(⋯)+0det(⋯)+(2−λ)det(−λ2731−λ201−λ).
We only have to compute one cofactor. To do so, first we clear the (3,3)-entry by performing the column replacement C3=C3+λC2, which does not change the determinant:
det(−λ2731−λ201−λ)=det(−λ27+2λ31−λ2+λ(1−λ)010).
Now we expand cofactors along the third row to find
det(−λ27+2λ31−λ2+λ(1−λ)010)=(−1)2+3det(−λ7+2λ32+λ(1−λ))=−(−λ(2+λ(1−λ))−3(7+2λ))=−λ3+λ2+8λ+21.
Therefore, we have
det(A)=(2−λ)(−λ3+λ2+8λ+21)=λ4−3λ3−6λ2−5λ+42.
It is often most efficient to use a combination of several techniques when computing the determinant of a matrix. Indeed, when expanding cofactors on a matrix, one can compute the determinants of the cofactors in whatever way is most convenient. Or, one can perform row and column operations to clear some entries of a matrix before expanding cofactors, as in the previous example.
We have several ways of computing determinants:
- Special formulas for 2×2 and 3×3 matrices.
This is usually the best way to compute the determinant of a small matrix, except for a 3×3 matrix with several zero entries. - Cofactor expansion.
This is usually most efficient when there is a row or column with several zero entries, or if the matrix has unknown entries. - Row and column operations.
This is generally the fastest when presented with a large matrix which does not have a row or column with a lot of zeros in it. - Any combination of the above.
Cofactor expansion is recursive, but one can compute the determinants of the minors using whatever method is most convenient. Or, you can perform row and column operations to clear some entries of a matrix before expanding cofactors.
Remember, all methods for computing the determinant yield the same number.
Cramer’s Rule and Matrix Inverses
Recall from Proposition 3.5.1 in Section 3.5 that one can compute the determinant of a 2×2 matrix using the rule
A=(d−b−ca)⟹A−1=1det(A)(d−b−ca).
We computed the cofactors of a 2×2 matrix in Example 4.2.3; using C11=d,C12=−c,C21=−b,C22=a, we can rewrite the above formula as
A−1=1det(A)(C11C21C12C22).
It turns out that this formula generalizes to n×n matrices.
Let A be an invertible n×n matrix, with cofactors Cij. Then
A−1=1det(A)(C11C21⋯Cn−1,1Cn1C12C22⋯Cn−1,2Cn2⋮⋮⋱⋮⋮C1,n−1C2,n−1⋯Cn−1,n−1Cn,n−1C1nC2n⋯Cn−1,nCnn).
The matrix of cofactors is sometimes called the adjugate matrix of A, and is denoted adj(A):
adj(A)=(C11C21⋯Cn−1,1Cn1C12C22⋯Cn−1,2Cn2⋮⋮⋱⋮⋮C1,n−1C2,n−1⋯Cn−1,n−1Cn,n−1C1nC2n⋯Cn−1,nCnn).
Note that the (i,j) cofactor Cij goes in the (j,i) entry the adjugate matrix, not the (i,j) entry: the adjugate matrix is the transpose of the cofactor matrix.
In fact, one always has A⋅adj(A)=adj(A)⋅A=det(A)In, whether or not A is invertible.
Use the Theorem 4.2.2 to compute A−1, where
A=(101011110).
Solution
The minors are:
A11=(1110)A12=(0110)A13=(0111)A21=(0110)A22=(1110)A23=(1011)A31=(0111)A32=(1101)A33=(1001)
The cofactors are:
C11=−1C12=1C13=−1C21=1C22=−1C23=−1C31=−1C32=−1C33=1
Expanding along the first row, we compute the determinant to be
det(A)=1⋅C11+0⋅C12+1⋅C13=−2.
Therefore, the inverse is
A−1=1det(A)(C11C21C31C12C22C32C13C23C33)=−12(−11−11−1−1−1−11).
It is clear from the previous example that (???) is a very inefficient way of computing the inverse of a matrix, compared to augmenting by the identity matrix and row reducing, as in Subsection Computing the Inverse Matrix in Section 3.5. However, it has its uses.
- If a matrix has unknown entries, then it is difficult to compute its inverse using row reduction, for the same reason it is difficult to compute the determinant that way: one cannot be sure whether an entry containing an unknown is a pivot or not.
- This formula is useful for theoretical purposes. Notice that the only denominators in (???) occur when dividing by the determinant: computing cofactors only involves multiplication and addition, never division. This means, for instance, that if the determinant is very small, then any measurement error in the entries of the matrix is greatly magnified when computing the inverse. In this way, (???) is useful in error analysis.
The proof of Theorem 4.2.2 uses an interesting trick called Cramer’s Rule, which gives a formula for the entries of the solution of an invertible matrix equation.
Let x=(x1,x2,…,xn) be the solution of Ax=b, where A is an invertible n×n matrix and b is a vector in Rn. Let Ai be the matrix obtained from A by replacing the ith column by b. Then
xi=det(Ai)det(A).
- Proof
-
First suppose that A is the identity matrix, so that x=b. Then the matrix Ai looks like this:
(10b1001b2000b3000b41).
Expanding cofactors along the ith row, we see that det(Ai)=bi, so in this case,
xi=bi=det(Ai)=det(Ai)det(A).
Now let A be a general n×n matrix. One way to solve Ax=b is to row reduce the augmented matrix (A∣b); the result is (In∣x). By the case we handled above, it is enough to check that the quantity det(Ai)/det(A) does not change when we do a row operation to (A∣b), since det(Ai)/det(A)=xi when A=In.
- Doing a row replacement on (A∣b) does the same row replacement on A and on Ai:
(a11a12a13b1a21a22a23b2a31a32a33b3)R2=R2−2R3→(a11a12a13b1a21−2a31a22−2a32a23−2a33b2−2b3a31a32a33b3)(a11a12a13a21a22a23a31a32a33)R2=R2−2R3→(a11a12a13a21−2a31a22−2a32a23−2a33a31a32a33)(a11b1a13a21b2a23a31b3a33)R2=R2−2R3→(a11b1a13a21−2a31b2−2b3a23−2a33a31b3a33).
In particular, det(A) and det(Ai) are unchanged, so det(A)/det(Ai) is unchanged. - Scaling a row of (A∣b) by a factor of c scales the same row of A and of Ai by the same factor:
(a11a12a13b1a21a22a23b2a31a32a33b3)R2=cR2→(a11a12a13b1ca21ca22ca23cb2a31a32a33b3)(a11a12a13a21a22a23a31a32a33)R2=cR2→(a11a12a13ca21ca22ca23a31a32a33)(a11b1a13a21b2a23a31b3a33)R2=cR2→(a11b1a13ca21cb2ca23a31b3a33).
In particular, det(A) and det(Ai) are both scaled by a factor of c, so det(Ai)/det(A) is unchanged. - Swapping two rows of (A∣b) swaps the same rows of A and of Ai:
(a11a12a13b1a21a22a23b2a31a32a33b3)R1⟷R2→(a21a22a23b2a11a12a13b1a31a32a33b3)(a11a12a13a21a22a23a31a32a33)R1⟷R2→(a21a22a23a11a12a13a31a32a33)(a11b1a13a21b2a23a31b3a33)R1⟷R2→(a21b2a23a11b1a13a31b3a33).
In particular, det(A) and det(Ai) are both negated, so det(Ai)/det(A) is unchanged.
- Doing a row replacement on (A∣b) does the same row replacement on A and on Ai:
Compute the solution of Ax=b using Cramer’s rule, where
A=(abcd)b=(12).
Here the coefficients of A are unknown, but A may be assumed invertible.
Solution
First we compute the determinants of the matrices obtained by replacing the columns of A with b:
A1=(1b2d)det(A1)=d−2bA2=(a1c2)det(A2)=2a−c.
Now we compute
det(A1)det(A)=d−2bad−bcdet(A2)det(A)=2a−cad−bc.
It follows that
x=1ad−bc(d−2b2a−c).
Now we use Cramer’s rule to prove the first Theorem 4.2.2 of this subsection.
The jth column of A−1 is xj=A−1ej. This vector is the solution of the matrix equation
Ax=A(A−1ej)=Inej=ej.
By Cramer’s rule, the ith entry of xj is det(Ai)/det(A), where Ai is the matrix obtained from A by replacing the ith column of A by ej:
Ai=(a11a120a14a21a221a24a31a320a34a41a420a44)(i=3,j=2).
Expanding cofactors along the ith column, we see the determinant of Ai is exactly the (j,i)-cofactor Cji of A. Therefore, the jth column of A−1 is
xj=1det(A)(CjiCj2⋮Cjn),
and thus
A−1=(|||x1x2⋯xn|||)=1det(A)(C11C21⋯Cn−1,1Cn1C12C22⋯Cn−1,2Cn2⋮⋮⋱⋮⋮C1,n−1C2,n−1⋯Cn−1,n−1Cn,n−1C1nC2n⋯Cn−1,nCnn).



