1.E: Whole Numbers (Exercises)
- Page ID
- 5266
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)1.1 - Introduction to Whole Numbers
Identify Counting Numbers and Whole Numbers
In the following exercises, determine which of the following numbers are (a) counting numbers (b) whole numbers.
- 0, 2, 99
- 0, 3, 25
- 0, 4, 90
- 0, 1, 75
Model Whole Numbers
In the following exercises, model each number using base-10 blocks and then show its value using place value notation.
- 258
- 104
Identify the Place Value of a Digit
In the following exercises, find the place value of the given digits.
- 472,981
(a) 8 (b) 4 (c) 1 (d) 7 (e) 2
- 12,403,295
(a) 4 (b) 0 (c) 1 (d) 9 (e) 3
Use Place Value to Name Whole Numbers
In the following exercises, name each number in words.
- 5,280
- 204,614
- 5,012,582
- 31,640,976
Use Place Value to Write Whole Numbers
In the following exercises, write each number as a whole number using digits.
- six hundred two
- fifteen thousand, two hundred fifty-three
- three hundred forty million, nine hundred twelve thousand, sixty-one
- two billion, four hundred ninety-two million, seven hundred eleven thousand, two
Round Whole Numbers
In the following exercises, round to the nearest ten.
- 412
- 648
- 3,556
- 2,734
In the following exercises, round to the nearest hundred.
- 38,975
- 26,849
- 81,486
- 75,992
1.2 - Add Whole Numbers
Use Addition Notation
In the following exercises, translate the following from math notation to words.
- 4 + 3
- 25 + 18
- 571 + 629
- 10,085 + 3,492
Model Addition of Whole Numbers
In the following exercises, model the addition.
- 6 + 7
- 38 + 14
Add Whole Numbers
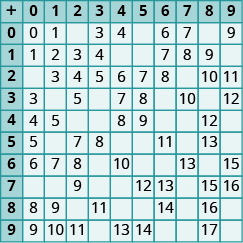
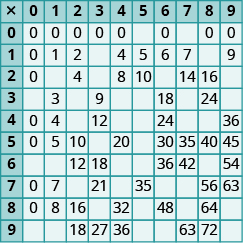
In the following exercises, fill in the missing values in each chart.
In the following exercises, add.
- (a) 0 + 19 (b) 19 + 0
- (a) 0 + 480 (b) 480 + 0
- (a) 7 + 6 (b) 6 + 7
- (a) 23 + 18 (b) 18 + 23
- 44 + 35
- 63 + 29
- 96 + 58
- 375 + 591
- 7,281 + 12,546
- 5,280 + 16,324 + 9,731
Translate Word Phrases to Math Notation
In the following exercises, translate each phrase into math notation and then simplify.
- the sum of 30 and 12
- 11 increased by 8
- 25 more than 39
- total of 15 and 50
Add Whole Numbers in Applications
In the following exercises, solve.
- Shopping for an interview Nathan bought a new shirt, tie, and slacks to wear to a job interview. The shirt cost $24, the tie cost $14, and the slacks cost $38. What was Nathan’s total cost?
- Running Jackson ran 4 miles on Monday, 12 miles on Tuesday, 1 mile on Wednesday, 8 miles on Thursday, and 5 miles on Friday. What was the total number of miles Jackson ran?
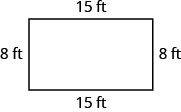
In the following exercises, find the perimeter of each figure.
1.3 - Subtract Whole Numbers
Use Subtraction Notation
In the following exercises, translate the following from math notation to words.
- 14 − 5
- 40 − 15
- 351 − 249
- 5,724 − 2,918
Model Subtraction of Whole Numbers
In the following exercises, model the subtraction.
- 18 − 4
- 41 − 29
Subtract Whole Numbers
In the following exercises, subtract and then check by adding.
- 8 − 5
- 12 − 7
- 23 − 9
- . 46 − 21
- 82 − 59
- 110 − 87
- 539 − 217
- 415 − 296
- 1,020 − 640
- 8,355 − 3,947
- 10,000 − 15
- 54,925 − 35,647
Translate Word Phrases to Math Notation
In the following exercises, translate and simplify.
- the difference of nineteen and thirteen
- subtract sixty-five from one hundred
- seventy-four decreased by eight
- twenty-three less than forty-one
Subtract Whole Numbers in Applications
In the following exercises, solve.
- Temperature The high temperature in Peoria one day was 86 degrees Fahrenheit and the low temperature was 28 degrees Fahrenheit. What was the difference between the high and low temperatures?
- Savings Lynn wants to go on a cruise that costs $2,485. She has $948 in her vacation savings account. How much more does she need to save in order to pay for the cruise?
1.4 - Multiply Whole Numbers
Use Multiplication Notation
In the following exercises, translate from math notation to words.
- 8 × 5
- 6 • 14
- (10)(95)
- 54(72)
Model Multiplication of Whole Numbers
In the following exercises, model the multiplication.
- 2 × 4
- 3 × 8
Multiply Whole Numbers
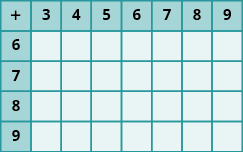
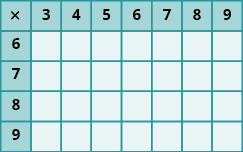
In the following exercises, fill in the missing values in each chart.
In the following exercises, multiply.
- 0 • 14
- (256)0
- 1 • 99
- (4,789)1
- (a) 7 • 4 (b) 4 • 7
- (25)(6)
- 9,261 × 3
- 48 • 76
- 64 • 10
- 1,000(22)
- 162 × 493
- (601)(943)
- 3,624 × 517
- 10,538 • 22
Translate Word Phrases to Math Notation
In the following exercises, translate and simplify.
- the product of 15 and 28
- ninety-four times thirty-three
- twice 575
- ten times two hundred sixty-four
Multiply Whole Numbers in Applications
In the following exercises, solve.
- Gardening Geniece bought 8 packs of marigolds to plant in her yard. Each pack has 6 flowers. How many marigolds did Geniece buy?
- Cooking Ratika is making rice for a dinner party. The number of cups of water is twice the number of cups of rice. If Ratika plans to use 4 cups of rice, how many cups of water does she need?
- Multiplex There are twelve theaters at the multiplex and each theater has 150 seats. What is the total number of seats at the multiplex?
- Roofing Lewis needs to put new shingles on his roof. The roof is a rectangle, 30 feet by 24 feet. What is the area of the roof?
1.5 - Divide Whole Numbers
Use Division Notation
Translate from math notation to words.
- 54 ÷ 9
- 42 / 7
- \(\dfrac{72}{8}\)
- \(6 \overline{\smash{)}48}\)
Model Division of Whole Numbers
In the following exercises, model.
- 8 ÷ 2
- \(3 \overline{\smash{)}12}\)
Divide Whole Numbers
In the following exercises, divide. Then check by multiplying.
- 14 ÷ 2
- \(\dfrac{32}{8}\)
- 52 ÷ 4
- \(26 \overline{\smash{)}26}\)
- \(\dfrac{97}{1}\)
- 0 ÷ 52
- 100 ÷ 0
- \(\dfrac{355}{5}\)
- 3828 ÷ 6
- \(31 \overline{\smash{)}1,519}\)
- \(\dfrac{7505}{25}\)
- 5,166 ÷ 42
Translate Word Phrases to Math Notation
In the following exercises, translate and simplify.
- the quotient of 64 and 16
- the quotient of 572 and 52
Divide Whole Numbers in Applications
In the following exercises, solve.
- Ribbon One spool of ribbon is 27 feet. Lizbeth uses 3 feet of ribbon for each gift basket that she wraps. How many gift baskets can Lizbeth wrap from one spool of ribbon?
- Juice One carton of fruit juice is 128 ounces. How many 4 ounce cups can Shayla fill from one carton of juice?
PRACTICE TEST
- Determine which of the following numbers are (a) counting numbers (b) whole numbers. $$0, 4, 87$$
- Find the place value of the given digits in the number 549,362.
(a) 9 (b) 6 (c) 2 (d) 5
- Write each number as a whole number using digits.
(a) six hundred thirteen (b) fifty-five thousand two hundred eight
- Round 25,849 to the nearest hundred.
Simplify.
- 45 + 23
- 65 − 42
- 85 ÷ 5
- 1,000 × 8
- 90 − 58
- 73 + 89
- (0)(12,675)
- 634 + 255
- \(\dfrac{0}{9}\)
- \(8 \overline{\smash{)}128}\)
- 145 − 79
- 299 + 836
- 7 • 475
- 8,528 + 704
- 35(14)
- \(\dfrac{26}{0}\)
- 733 − 291
- 4,916 − 1,538
- 495 ÷ 45
- 52 × 983
Translate each phrase to math notation and then simplify.
- The sum of 16 and 58
- The product of 9 and 15
- The difference of 32 and 18
- The quotient of 63 and 21
- Twice 524
- 29 more than 32
- 50 less than 300
In the following exercises, solve.
- LaVelle buys a jumbo bag of 84 candies to make favor bags for her son’s party. If she wants to make 12 bags, how many candies should she put in each bag?
- Last month, Stan’s take-home pay was $3,816 and his expenses were $3,472. How much of his take-home pay did Stan have left after he paid his expenses?
- Each class at Greenville School has 22 children enrolled. The school has 24 classes. How many children are enrolled at Greenville School?
- Clayton walked 12 blocks to his mother’s house, 6 blocks to the gym, and 9 blocks to the grocery store before walking the last 3 blocks home. What was the total number of blocks that Clayton walked?