11.1: The Trigonometric Ratios
- Page ID
- 122907
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)2.1 Side and Angle Relationships
Homework 2.1
1. The sum of the angles is not \(180^{\circ}\)
3. The exterior angle is not equal to the sum of the opposite interior angles.
5. The sum of the acute angles is not \(90^{\circ}\)
7. The largest side is not opposite the largest angle.
9. The Pythagorean theorem is not satisfied.
11. \(5^2+12^2=13^2\), but the angle opposite the side of length 13 is \(85^{\circ}\).
13. \(4 < x < 16\)
15. \(0 < x < 16\)
17. 21 in
19. \(6\sqrt{2}\)in
21. \(w = 6\sqrt{10}\)in
23. 29
25. \(\sqrt{3}\)
27. No
29. Yes
31. No
33. The distance from \((0,0)\) to \((3,3)\) is \(3 \sqrt{2}\), and the distance from \((3,3)\) to \((6,0)\) is also \(3 \sqrt{2}\), so the triangle is isosceles. The distance from \((0,0)\) to \((6,0)\) is 6 , and \((3 \sqrt{2})^2+(3 \sqrt{2})^2=6^2\) so the triangle is a right triangle.
35. 25 ft
37. \(\alpha=30^{\circ}, \beta=60^{\circ}, h=\sqrt{3}\)
39. \(8 \sqrt{3}\) in
41.
a No
b Yes
43.
a \((-1,0)\) and \((1,0) ; 2\)
b \(\sqrt{(p+1)^2+q^2}\) and \(\sqrt{(p-1)^2+q^2}\)
c
\begin{aligned}
\left(\sqrt{(p+1)^2+q^2}\right)^2 & +\left(\sqrt{(p-1)^2+q^2}\right)^2 \\
& =p^2+2 p+1+q^2+p^2-2 p+1+q^2 \\
& =2 p^2+2+2 q^2=2+2\left(p^2+q^2\right) \\
& =2+2(1)=4
\end{aligned}
2.2 Right Triangle Trigonometry
Homework 2.2
1.
a 0.91
b 0.91
c 0.9063
2.
a 0.77
b 0.77
c 0.7660
5.
a \(4\sqrt{13} \approx 14.42\)
b \(\sin \theta = 0.5547, \cos \theta = 0.8321, \tan \theta = 0.6667
7.
a \(4\sqrt{15} \approx 15.49\)
b \(\sin \theta = 0.9682, \cos \theta = 0.2500, \tan \theta = 3.8730\)
9.
a \(2\sqrt{67} \approx 15.49\)
b \(\sin \theta = 0.2116, \cos \theta = 0.9774, \tan \theta = 0.2165\)
11.
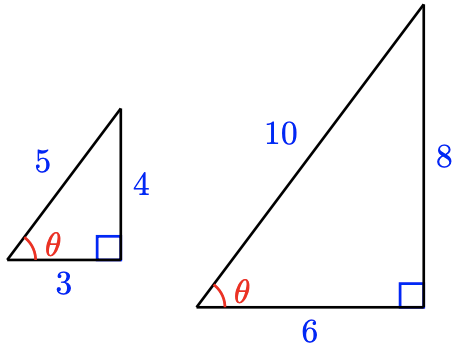
(Answers may vary)
13.
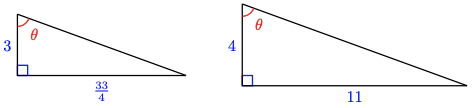
(Answers may vary)
15.

(Answers may vary)
17. 14.41
19. 37.86
21. 86.08
23.

25.

27.
a 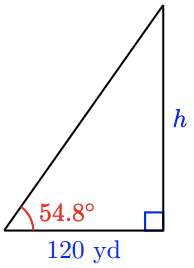
b \(\tan 54.8^{\circ} = \dfrac{h}{20}, 170.1\) yd
29.
a 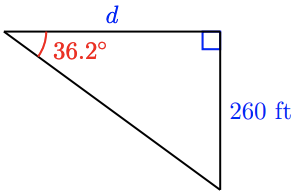
b \(\tan 36.2^{\circ} = \dfrac{260}{d}, 355.2\) ft
31.
a 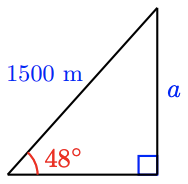
b \(\sin 48^{\circ} = \dfrac{a}{1500}, 1114.7\)m
33.
a 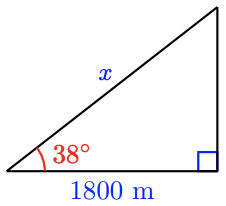
b \(\cos 38^{\circ} = \dfrac{1800}{x}, 2284.2\)m
35. \(x = \dfrac{82}{\tan \theta}\)
37. \(x = 11 \sin \theta\)
39. \(x = \dfrac{9}{\cos \theta}\)
41. \(36 \sin 25^{\circ} \approx 15.21\)
43. \(46 \sin 20^{\circ} \approx 15.73\)
45. \(12 \sin 40^{\circ} \approx 7.71\)
47.
| \(\sin\) | \(\cos\) | \(\tan\) | |
| \(\theta\) | \(\dfrac{3}{5}\) | \(\dfrac{4}{5}\) | \(\dfrac{3}{4}\) |
| \(\phi\) | \(\dfrac{4}{5}\) | \(\dfrac{3}{5}\) | \(\dfrac{4}{3}\) |
49.
| \(\sin\) | \(\cos\) | \(\tan\) | |
| \(\theta\) | \(\dfrac{1}{\sqrt{5}}\) | \(\dfrac{2}{\sqrt{5}}\) | \(\dfrac{1}{2}\) |
| \(\phi\) | \(\dfrac{2}{\sqrt{5}}\) | \(\dfrac{1}{\sqrt{5}}\) | 2 |
51.
a \(\theta\) and \(\phi\) are complements.
b \(\sin \theta=\cos \phi\) and \(\cos \theta=\sin \phi\). The side opposite \(\theta\) is the side adjacent to \(\phi\), and vice versa.
53.
a As \(\theta\) increases, \(\tan \theta\) increases also. The side opposite \(\theta\) increases in length while the side adjacent to \(\theta\) remains fixed.
b As \(\theta\) increases, \(\cos \theta\) decreases. The side adjacent to \(\theta\) remains fixed while the hypotenuse increases in length.
55. As \(\theta\) decreases toward \(0^{\circ}\), the side opposite \(\theta\) approaches a length of 0, so \(\sin \theta\) approaches 0. But as \(\theta\) increases toward \(90^{\circ}\), the length of the side opposite \(\theta\) approaches the length of the hypotenuse, so \(\sin \theta\) approaches 1.
57. The triangle is not a right triangle.
59. \(\dfrac{21}{20}\) is the ratio of hypotenuse to the adjacent side, which is the reciprocal of \(\cos \theta\).
61.
a \(0.2358\)
b sine
c \(48^{\circ}\)
d \(77^{\circ}\)
63.
a \(\dfrac{5}{12}\)
b 3
c \(\dfrac{2}{3}\)
d \(\dfrac{2}{\sqrt{7}}\)
65. Although the triangles may differ in size, the ratio of the side adjacent to the angle to the hypotenuse of the triangle remains the same because the triangles would all be similar, and hence corresponding sides are proportional.
67.
a \(\dfrac{2}{3}\)
b \(\dfrac{2}{3}\)
c 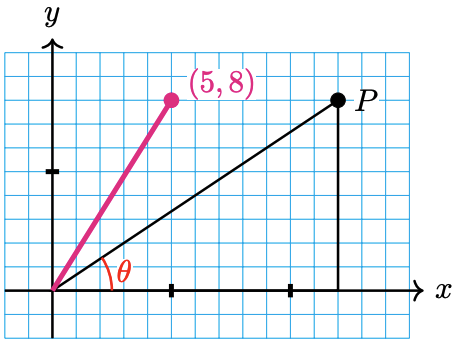
2.3 Solving Right Triangles
Homework 2.3
1. \(A = 61^{\circ}, a = 25.26, c = 28.88\)
3. \(A = 68^{\circ}, a = 0.93, b = 0.37\)
5.
a 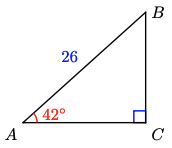
b \(B = 48^{\circ}, a = 17.4, b = 19.3\)
7.
a 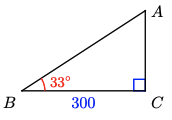
b \(A=57^{\circ}, b=194.4, c=357.7\)
9.
a 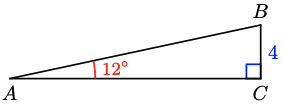
b \(B=78^{\circ}, b=18.8, c=19.2\)
11.
a 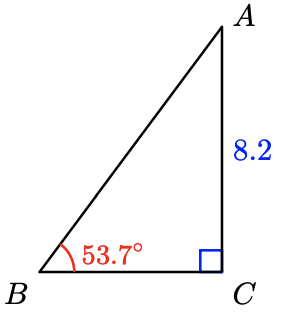
b
- Solve \(\sin 53.7^{\circ} = \dfrac{8.2}{c}\) for \(c\).
- Solve \(\tan 53.7^{\circ} = \dfrac{8.2}{a}\) for \(a\).
- Subtract \(53.7^{\circ}\) from \(90^{\circ}\) to find \(A\).
13.
a 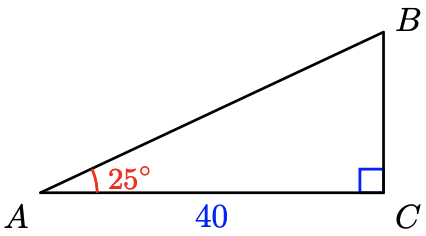
b
- Solve \(\cos 25^{\circ} = \dfrac{40}{c}\) for \(c\).
- Solve \(\tan 25^{\circ} = \dfrac{a}{40}\) for \(a\).
- Subtract \(25^{\circ}\) from \(90^{\circ}\) to find \(B\).
15.
a 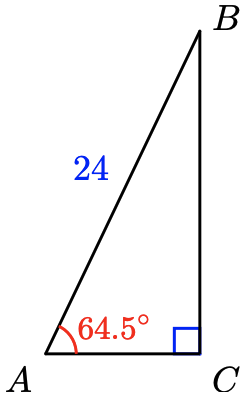
b
- Solve \(\sin 64.5^{\circ} = \dfrac{a}{24}\) for \(a\).
- Solve \(\cos 64.5^{\circ} = \dfrac{b}{24}\) for \(b\).
- Subtract \(64.5^{\circ}\) from \(90^{\circ}\) to find \(B\).
17. \(74.2^{\circ}\)
19. \(56.4^{\circ}\)
21. \(66.0^{\circ}\)
23. \(11.5^{\circ}\)
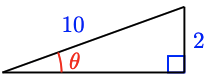
25. \(56.3^{\circ}\)
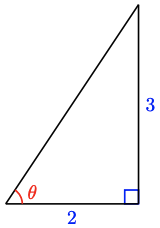
27. \(73.5^{\circ}\)
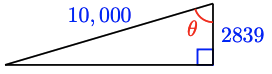
29. \(\cos 15^{\circ} = 0.9659\) and \(\cos ^{-1} 0.9659 = 15^{\circ}\)
31. \(\tan 65^{\circ} = 2.1445\) and \(\tan ^{-1} 2.1445 = 65^{\circ}\)
33. \(\sin ^{-1} (0.6) \approx 36.87^{\circ}\) is the angle whose sine is 0.6. \((\sin 6^{\circ})^{-1} \approx 9.5668\) is the reciprocal of \(\sin 6^{\circ}\).
35.
a 
b \(\sin \theta = \dfrac{1806}{3(2458)}, 14.6^{\circ}\)
37.
a 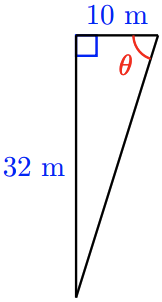
b \(\tan \theta=\dfrac{32}{10}, 72.6^{\circ}\)
39.
a 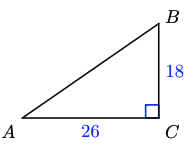
b \(c=10 \sqrt{10} \approx 31.6, A \approx 34.7^{\circ}, B \approx 55.3^{\circ}\)
41.
a 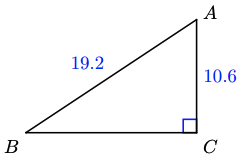
b \(a=\sqrt{256.28} \approx 16.0, A \approx 56.5^{\circ}, B \approx 33.5^{\circ}\)
43.
a 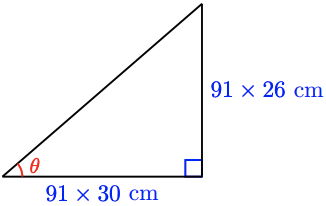
b \(\tan ^{-1}\left(\dfrac{26}{30}\right) \approx 40.9^{\circ}, \quad 91 \sqrt{1676} \approx 3612.6 \mathrm{~cm}\)
45.
a 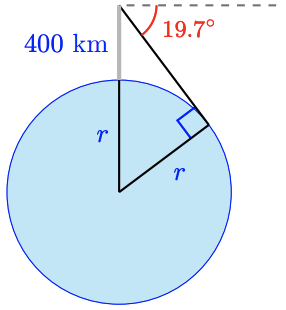
b 6415 km
47.
a 
b 462.9 ft
49. (a) and (b)
51. (a) and (d)
53. \(\dfrac{\sqrt{3}}{2} \approx 0.8660\)
55. \(\dfrac{1}{\sqrt{3}} = \dfrac{\sqrt{3}}{3} \approx 0.5774\)
57. 1.0000
59.
| \(\theta\) | \(0^{\circ}\) | \(30^{\circ}\) | \(45^{\circ}\) | \(60^{\circ}\) | \(90^{\circ}\) |
| \(\sin \theta\) | 0 | \(\dfrac{1}{2}\) | \(\dfrac{\sqrt{2}}{2}\) | \(\dfrac{\sqrt{3}}{2}\) | 1 |
| \(\cos \theta\) | 1 | \(\dfrac{\sqrt{3}}{2}\) | \(\dfrac{\sqrt{2}}{2}\) | \(\dfrac{1}{2}\) | 0 |
| \(\tan \theta\) | 0 | \(\dfrac{1}{\sqrt{3}}\) | 1 | \(\sqrt{3}\) | undefined |
61.
a smaller
b larger
c larger
63. \(a=3 \sqrt{3}, b=3, B=30^{\circ}\)
65. \(a=b=4 \sqrt{2}, B=45^{\circ}\)
67. \(e=4, f=4 \sqrt{3}, F=120^{\circ}\)
69. \(d=2 \sqrt{3}, e=2 \sqrt{2}, f=\sqrt{2}+\sqrt{6}, F=75^{\circ}\)
71. \(\a=20, b=20, c=20 \sqrt{2})
73.
a \(32 \sqrt{3} \mathrm{~cm}\)
b \(128 \sqrt{3} \mathrm{sq} \mathrm{cm}\)
75.
a \(10 \mathrm{sq} \mathrm{cm}\)
b \(10 \sqrt{2} \mathrm{sq} \mathrm{cm}\)
c \(10 \sqrt{3} \mathrm{sq} \mathrm{cm}\)
2.4 Chapter 2 Summary and Review
Chapter 2 Review Problems
1. If \(C>93^{\circ}\), then \(A+B+C>180^{\circ}\)
3. If \(A<B<58^{\circ}\), then \(A+B+C<180^{\circ}\)
5. If \(C>50^{\circ}\), then \(A+B+C>180^{\circ}\)
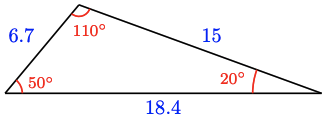
7. 
9. \(a = 97\)
11. \(c = 52\)
13. Yes
15. \(\theta=35.26^{\circ}\)
17. No. \(a=6, c=10\) or \(a=9, c=15\)
19.
a \(w=86.05\)
b \(\sin \theta=0.7786, \quad \cos \theta=0.6275, \quad \tan \theta=1.2407\)
21.
a \(y=16.52\)
b \(\sin \theta=0.6957, \quad \cos \theta=0.7184, \quad \tan \theta=0.9684\)
23. \(a = 7.89\)
25. \(x = 3.57\)
27. \(b = 156.95\)
29. \(A=30^{\circ}, a=\dfrac{23 \sqrt{3}}{3}, c=\dfrac{46 \sqrt{3}}{3}\)
31. \(F=105^{\circ}, d=10 \sqrt{2}, e=20, f=10+10 \sqrt{3}\)
33. 3 cm
35. 43.30 cm
37. 15.92 m
39. \(114.02 \mathrm{ft}, 37.87^{\circ}\)
41.
a \(60.26^{\circ}\)
b \(60.26^{\circ}\)
c \(m=\dfrac{7}{4}=\tan \theta\)
43.
a \(c^2\)
b \(b-a,(b-a)^2\)
c \(\dfrac{1}{2} a b\)
d \(4\left(\dfrac{1}{2} a b\right)+(a-b)^2=2 a b+b^2-2 a b+a^2=a^2+b^2\)


