11.3: Trigonometric Functions
- Page ID
- 122920
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)4.1 Angles and Rotation
Homework 4.1
1.
a \(216^{\circ}\)
b \(108^{\circ}\)
c \(480^{\circ}\)
d \(960^{\circ}\)
3.
a \(\dfrac{1}{8}\)
b \(\dfrac{5}{6}\)
c \(\dfrac{3}{2}\)
d \(\dfrac{7}{6}\)
5.
a \(\dfrac{2}{3}\)
b \(\dfrac{5}{3}\)
7. \(60^{\circ}\)
9. \(60^{\circ}\)
11. \(14^{\circ}\)
13. \(400^{\circ} \text{ and } -320^{\circ}\) (Answers vary.)
15. \(575^{\circ} \text{ and } -145^{\circ}\) (Answers vary.)
17. \(665^{\circ} \text{ and } -55^{\circ}\) (Answers vary.)
19. \(295^{\circ}\)
21. \(70^{\circ}\)
23. \(315^{\circ}\)
25. \(80^{\circ}\)
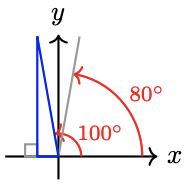
27. \(36^{\circ}\)
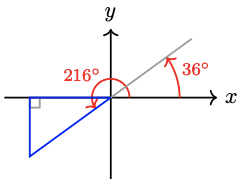
29. \(63^{\circ}\)
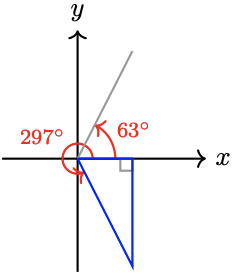
31. \(165^{\circ}, 95^{\circ}, 345^{\circ}\)
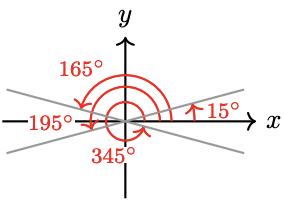
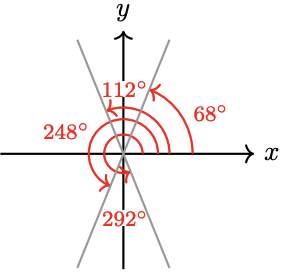
33. \(140^{\circ}, 220^{\circ}, 320^{\circ}\)
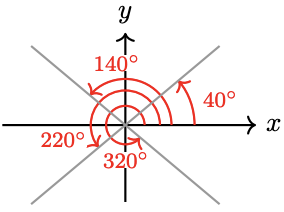
35. \(112^{\circ}, 248^{\circ}, 292^{\circ}\)
37. −0.9205
39. −0.7193
41. 4.705
43. −0.7193
45.
a \(120^{\circ}\)
b \(135^{\circ}\)
c \(150^{\circ}\)
d \(210^{\circ}\)
e \(225^{\circ}\)
f \(240^{\circ}\)
g \(300^{\circ}\)
h \(315^{\circ}\)
i \(330^{\circ}\)
47.
a 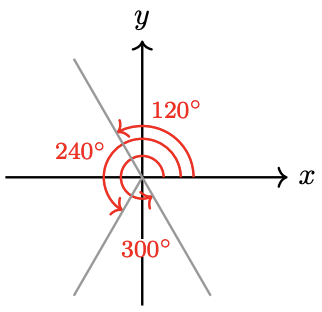
b
\begin{aligned}
\mathrm{b} \sin 120^{\circ} & =\dfrac{\sqrt{3}}{2}, \cos 120^{\circ}=\dfrac{-1}{2}, \tan 120^{\circ}=-\sqrt{3}, \\
\sin 240^{\circ} & =\dfrac{-\sqrt{3}}{2}, \cos 240^{\circ}=\dfrac{-1}{2}, \tan 240^{\circ}=\sqrt{3}, \\
\sin 300^{\circ} & =\dfrac{-\sqrt{3}}{2}, \cos 300^{\circ}=\dfrac{1}{2}, \tan 300^{\circ}=-\sqrt{3}
\end{aligned}
49.
a 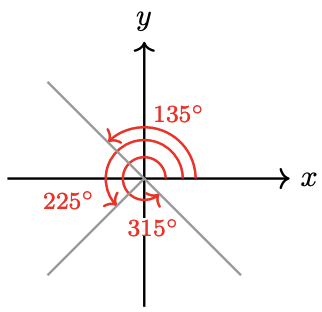
b
\begin{aligned}
\text { b } \sin 135^{\circ} & =\dfrac{1}{\sqrt{2}}, \quad \cos 135^{\circ}=\dfrac{-1}{\sqrt{2}}, \quad \tan 135^{\circ}=-1, \\
\sin 225^{\circ} & =\dfrac{-1}{\sqrt{2}}, \quad \cos 225^{\circ}=\dfrac{-1}{\sqrt{2}}, \quad \tan 225^{\circ}=1, \\
\sin 315^{\circ} & =\dfrac{-1}{\sqrt{2}}, \quad \cos 315^{\circ}=\dfrac{1}{\sqrt{2}}, \quad \tan 315^{\circ}=-1
\end{aligned}
51.
a III and IV
b II and III
c I and III
53.
a \(0^{\circ}\) and \(180^{\circ}\)
b \(90^{\circ}\) and \(270^{\circ}\)
55. \(105^{\circ}\)
57. \(264^{\circ}\)
59. \(313^{\circ}\)
61. \(83^{\circ}, 263^{\circ}\)
63. \(23^{\circ}, 337^{\circ}\)
65. \(265^{\circ}, 275^{\circ}\)
67. \(156^{\circ}, 204^{\circ}\)
69. \(246^{\circ}, 294^{\circ}\)
71. \(149^{\circ}, 329^{\circ}\)
73. \((-2\sqrt{2}, 2\sqrt{2})\)
75. \((\dfrac{3}{2}, \dfrac{3\sqrt{3}}{2})\)
77. \((\dfrac{-\sqrt{3}}{2}, \dfrac{-1}{2})\)
79.
a (−0.9, −0.3)
b (−0.940, −0.342)
c (−1.9, −0.7)
81.
a (−0.9, 0.3)
b (−0.940, 0.342)
c (−1.9, 0.7)
83. Sides of similar triangles are proportional.
4.2 Graphs of Trigonometric Functions
Homework 4.2
1. \((4 \sqrt{2},-4 \sqrt{2})\)
3. \((-10,-10 \sqrt{3})\)
5. \(\left(\dfrac{-15 \sqrt{3}}{2}, \dfrac{15}{2}\right)\)
7. \((-1.25,-5.87)\)
9. \((5.70,-11.86)\)
11. \((9.46,-3.26)\)
13.
a 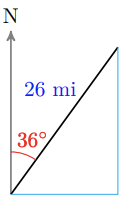
b 15.3 mi east, 21 mi north
15.
a 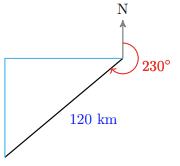
b 91.9 km west, 77.1 km south
17.
a 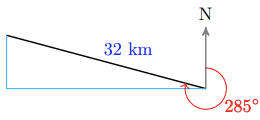
b 30.9 km west, 8.3 km north
19.
| Angle | \(0^{\circ}\) | \(10^{\circ}\) | \(20^{\circ}\) | \(30^{\circ}\) | \(40^{\circ}\) | \(50^{\circ}\) | \(60^{\circ}\) | \(70^{\circ}\) | \(80^{\circ}\) | \(90^{\circ}\) |
| \(x\)-coordinate | 1 | 0.98 | 0.94 | 0.97 | 0.77 | 0.64 | 0.5 | 0.34 | 0.17 | 0 |
| Angle | \(100^{\circ}\) | \(110^{\circ}\) | \(120^{\circ}\) | \(130^{\circ}\) | \(140^{\circ}\) | \(150^{\circ}\) | \(160^{\circ}\) | \(170^{\circ}\) | \(180^{\circ}\) |
| \(x\)-coordinate | -0.17 | -0.34 | -0.5 | -0.64 | -0.77 | -0.87 | -0.94 | -0.98 | -1 |
| Angle | \(190^{\circ}\) | \(200^{\circ}\) | \(210^{\circ}\) | \(220^{\circ}\) | \(230^{\circ}\) | \(240^{\circ}\) | \(250^{\circ}\) | \(260^{\circ}\) | \(270^{\circ}\) |
| \(x\)-coordinate | -0.98 | -0.94 | -0.87 | -0.77 | -0.64 | -0.5 | -0.34 | -0.17 | 0 |
| Angle | \(280^{\circ}\) | \(290^{\circ}\) | \(300^{\circ}\) | \(310^{\circ}\) | \(320^{\circ}\) | \(330^{\circ}\) | \(340^{\circ}\) | \(350^{\circ}\) | \(360^{\circ}\) |
| \(x\)-coordinate | 0.17 | 0.34 | 0.5 | 0.64 | 0.77 | 0.87 | 0.94 | 0.98 | 1 |
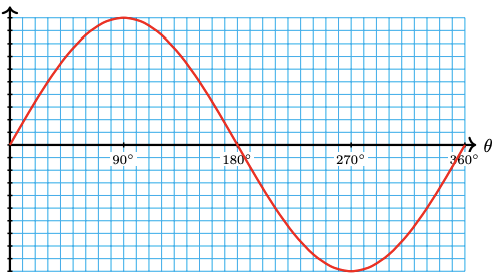
21. 
23. 
25. 
27.
a \(\left(-225^{\circ}, \dfrac{1}{\sqrt{2}}\right)\)
b \(\left(-135^{\circ}, \dfrac{-1}{\sqrt{2}}\right)\)
c \(\left(-90^{\circ},-1\right)\)
d \(\left(45^{\circ}, \dfrac{1}{\sqrt{2}}\right)\)
e \(\left(180^{\circ}, 0\right)\)
f \(\left(315^{\circ}, \dfrac{-1}{\sqrt{2}}\right)\)
29.
a \(\left(-240^{\circ}, \dfrac{-1}{2}\right)\)
b \(\left(-210^{\circ}, \dfrac{-\sqrt{3}}{2}\right)\)
c \(\left(-60^{\circ}, \dfrac{-1}{2}\right)\)
d \(\left(30^{\circ}, \dfrac{\sqrt{3}}{2}\right)\)
e \(\left(120^{\circ}, \dfrac{-1}{2}\right)\)
f \(\left(270^{\circ}, 0\right)\)
30.
a
| \(\theta\) | \(0^{\circ}\) | \(90^{\circ}\) | \(180^{\circ}\) | \(270^{\circ}\) | \(360^{\circ}\) |
| \(f(\theta)\) | 0 | 1 | 0 | -1 | 0 |
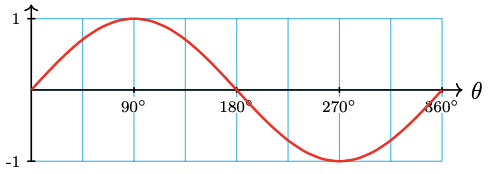
b
| \(\theta\) | \(0^{\circ}\) | \(90^{\circ}\) | \(180^{\circ}\) | \(270^{\circ}\) | \(360^{\circ}\) |
| \(f(\theta)\) | 1 | 0 | -1 | 0 | 1 |

33. \(\dfrac{7}{2}\)
35. \(-2\sqrt{2} - 1\)
37. 2
39. \(\dfrac{21}{2}\)
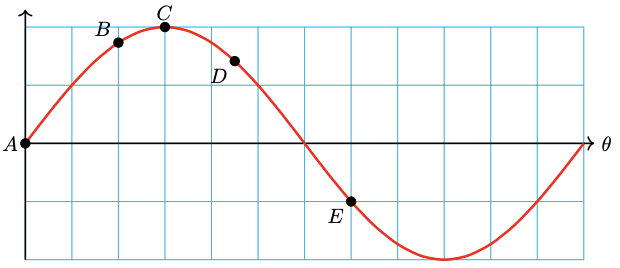
41. 
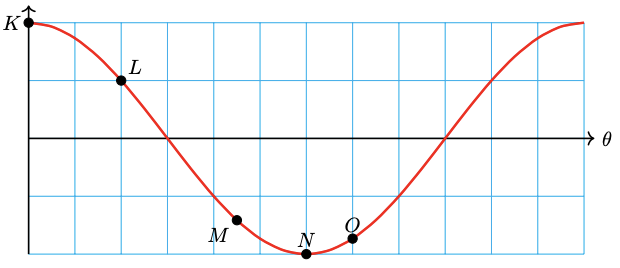
43. 
45.
a \(36.9^{\circ}, 143.1^{\circ}\)
b 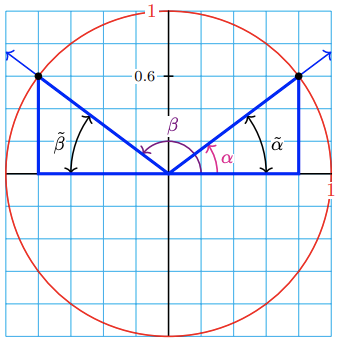
47.
a \(72.5^{\circ}, 287.5^{\circ}\)
b 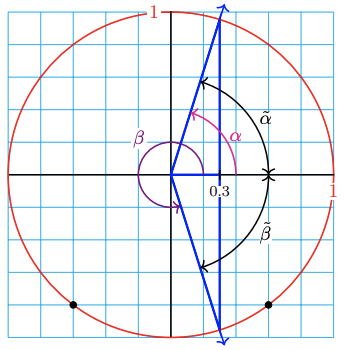
49. \(36.9^{\circ}, 143.1^{\circ}\)
51. \(72.5^{\circ}, 287.5^{\circ}\)
53. \(191.5^{\circ}, 348.5^{\circ}\)
55. \(154.2^{\circ}, 205.8^{\circ}\)
57.
a
| \(\theta\) | \(81^{\circ}\) | \(82^{\circ}\) | \(83^{\circ}\) | \(84^{\circ}\) | \(85^{\circ}\) | \(86^{\circ}\) | \(87^{\circ}\) | \(88^{\circ}\) | \(89^{\circ}\) |
| \(\tan \theta\) | 6.314 | 7.115 | 8.114 | 9.514 | 11.43 | 14.301 | 19.081 | 28.636 | 57.29 |
b \(\tan \theta\) approaches \(\infty\)
c
| \(\theta\) | \(99^{\circ}\) | \(98^{\circ}\) | \(97^{\circ}\) | \(96^{\circ}\) | \(95^{\circ}\) | \(94^{\circ}\) | \(93^{\circ}\) | \(92^{\circ}\) | \(91^{\circ}\) |
| \(\tan \theta\) | -6.314 | -7.115 | -8.144 | -9.514 | -11.43 | -14.301 | -19.081 | -28.636 | -57.29 |
d \(\tan \theta\) approaches \(-\infty\)
e The calculator gives an error message because \(\tan 90^{\circ}\) is undefined.
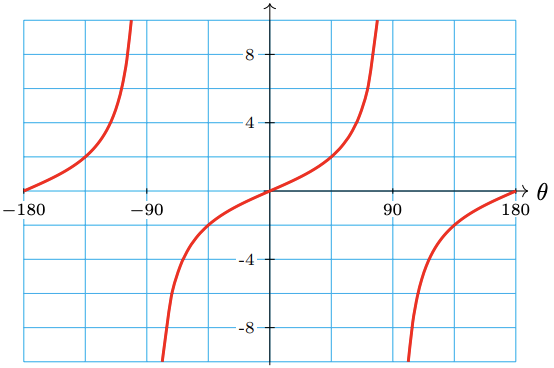
59. 
61. \(51.34^{\circ}\)
63. \(159.44^{\circ}\)
65. \(y+5=\left(\tan 28^{\circ}\right)(x-3)\) or \(y+5=0.532(x-3)\)
67. \(y-12=\left(\tan 112^{\circ}\right)(x+8)\) or \(y-12=-2.475(x+8)\)
69.
| \(\alpha\) | \(0^{\circ}\) | \(15^{\circ}\) | \(30^{\circ}\) | \(45^{\circ}\) | \(60^{\circ}\) | \(75^{\circ}\) | \(90^{\circ}\) | \(105^{\circ}\) | \(120^{\circ}\) | \(135^{\circ}\) | \(150^{\circ}\) | \(165^{\circ}\) | \(180^{\circ}\) |
| \(m\) | 0 | 0.268 | 0.577 | 1 | 1.732 | 3.732 | -- | -3.732 | -1.732 | -1 | -0.577 | -0.268 | 0 |
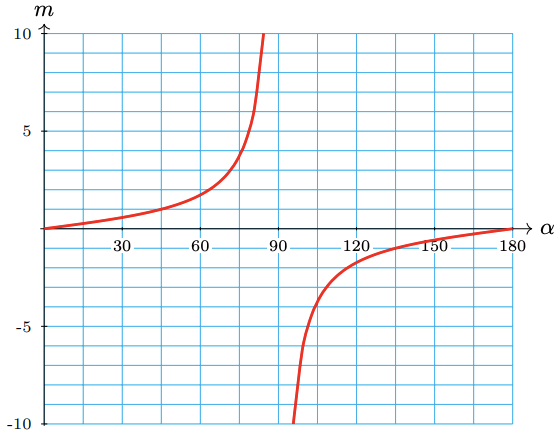
a The slope increases toward \(\infty\).
b The slope decreases toward \(-\infty\).
4.3 Periodic Functions
Homework 4.3
1.
a 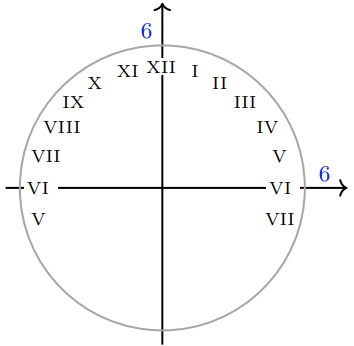
b
| \(t\) | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
| \(\theta\) | \(90^{\circ}\) | \(60^{\circ}\) | \(30^{\circ}\) | \(0^{\circ}\) | \(330^{\circ}\) | \(300^{\circ}\) | \(270^{\circ}\) | \(240^{\circ}\) | \(210^{\circ}\) | \(180^{\circ}\) | \(150^{\circ}\) | \(120^{\circ}\) | \(90^{\circ}\) |
| \(y = f(t)\) | 6 | \(3 \sqrt{3}\) | 3 | 0 | -3 | \(-3\sqrt{3}\) | -6 | \(-3\sqrt{3}\) | -3 | 0 | 3 | \(3\sqrt{3}\) | 6 |
c 
d The graph from \(t=24\) to \(t=48\) will be exactly the same shape as the graph from \(t=0\) to \(t=24\). \(f(t+24) = f(t)\) says that the ant's \(y\)-coordinate 24 seconds after a time \(t\) is the same as its \(y\)-coordinate at time \(t\).
3.
a 2, 5, 5
b 5
c
| \(d\) | 0 | 2 | 5 | 8 | 10 | 12 | 15 | 18 | 20 | 22 | 25 | 28 | 30 | 32 | 35 | 38 | 40 |
| \(y\) | 0 | 2 | 5 | 5 | 5 | 5 | 5 | 2 | 0 | -2 | -5 | -5 | -5 | -5 | -5 | -2 | 0 |
d 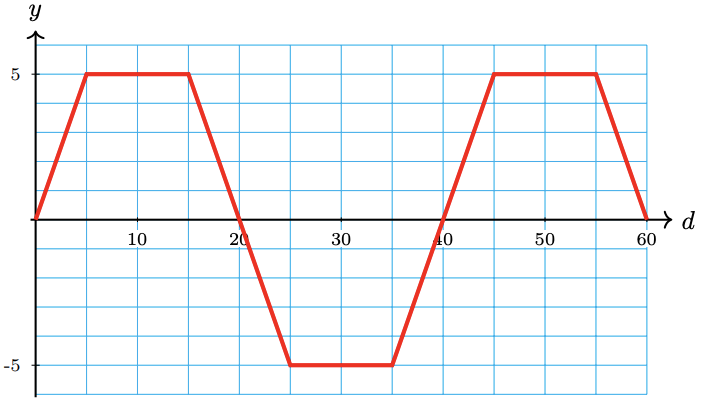
5.
a He will be back in the same position.
b \(f(d+40) = f(d)\)
c The graph for \(0 \leq d \leq 40\) will be exactly the same shape as the graph for \(40 \leq d \leq 80\).
d Every 40 unit wide piece of the graph will be identical to the previous 40 units.
7. \(y = 6 \sin \theta\)
9. \(y = \cos \theta - 5\)
11. \(y = \sin (4\theta)\)
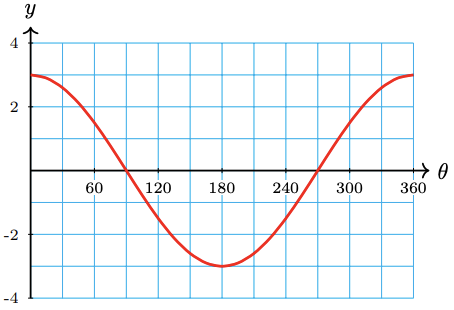
13. 
15. 
17. 
19. amp = 4, period = \(360^{\circ}\), midline: \(y = 3\)
21. amp = 5, period = \(180^{\circ}\), midline: \(y = 0\)
23. amp = 3, period = \(120^{\circ}\), midline: \(y = -4\)
25.
a amp = 1, period = \(90^{\circ}\), midline: \(y = 0\)
b \(y = \sin 4 \theta\)
27.
a amp = 1, period = \(360^{\circ}\), midline: \(y = 3\)
b \(y = 3 + \cos \theta\)
29.
a amp = 4, period = \(360^{\circ}\), midline: \(y = -2\)
b \(y = -2 + 4\sin \theta\)
31.
a amp = 2, period = \(120^{\circ}\), midline: \(y = 2\)
b \(y = 2 + 2\cos 3 \theta\)
33. \(y = 2 + 5 \cos \theta\)
35. \(y = -4 \sin \theta\)
37. \(y = -4 + 6\sin 3 \theta\) (Answers vary)
39. \(y = 3 + 2 \cos \theta\) (Answers vary)
41. \(y = 12 \cos 2 \theta\)
43. \(A\left(0^{\circ},-3\right), B\left(135^{\circ}, \dfrac{3}{\sqrt{2}}\right), C\left(300^{\circ}, \dfrac{-3}{2}\right)\)
45. \(P\left(112.5^{\circ}, 1\right), Q\left(180^{\circ}, 0\right), R\left(337.5^{\circ},-1\right)\)
47. \(X\left(45^{\circ},-3+\dfrac{1}{\sqrt{2}}\right), Y\left(90^{\circ},-3\right) Z\left(300^{\circ},-2\right)\)
49. not periodic
51. Periodic with period 4
53.
a 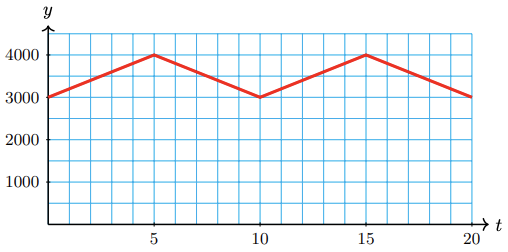
b 10 minutes
55.
a 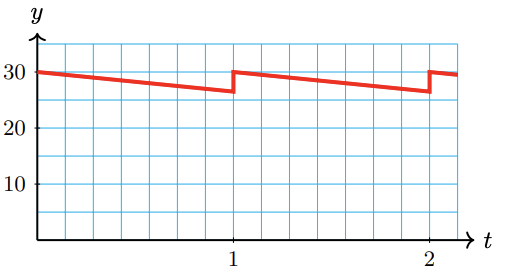
b 1 week
57.
a 
b period 1 sec, midline \(y = 12\), amp 10 inches
59.
a 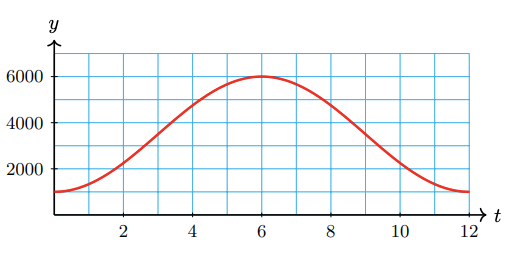
b period 1 year, midline \(y = 3500\), amp 2500
61.
a 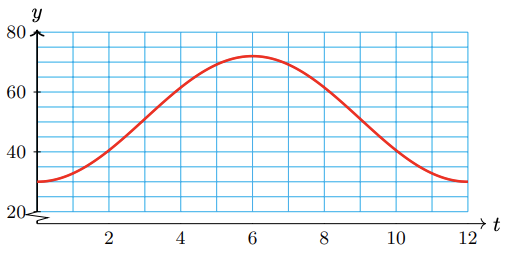
b period 1 year, midline \(y = 51\), amp 21
63.
a. IV
b. III
c. II
d. I
65.
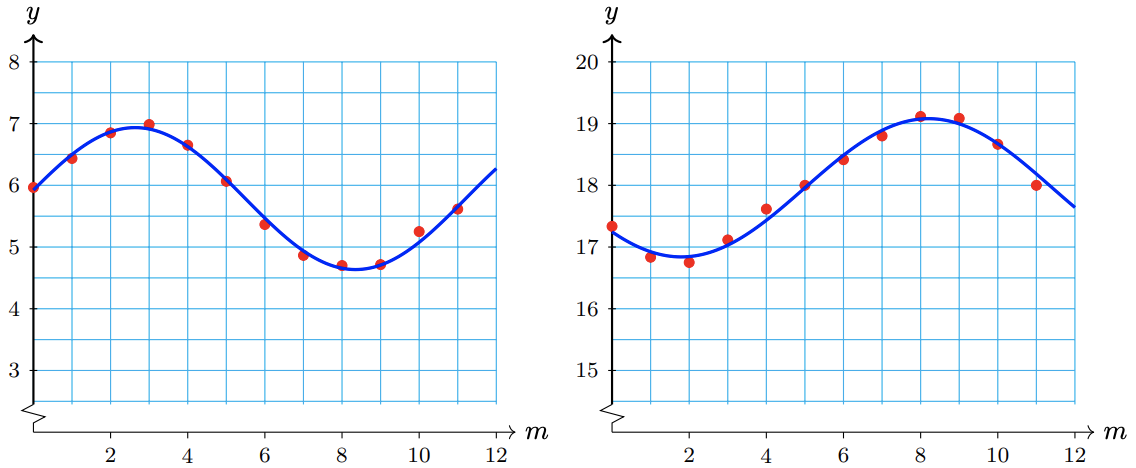
67.
a Emotional high: Oct 5 and Nov 3, low: Oct 19; Physical high: Sep 30 and Oct 23, low: Oct 12 and Nov 4; Intellectual high: Oct 10, low: Oct 26
b Emotional: 28 days, physical: 23 days, intellectual: 32 days
c 5152 days
69.
a periodic, period 8
b 4, midline: \(y = 3\)
c \(k = 8\)
d \(a = 3, b = 7\)
71.
a systolic 120 mm Hg, diastolic 80 mm Hg, pulse pressure 40 mm Hg.
b \(99 \dfrac{1}{3}\)
c 72 beats per minute
73.
a 69 hours.
b 2.2 to 3.5
c The larger dip corresponds to when the brighter star is eclipsed, the smaller dip corresponds to when the dimmer star is eclipsed.
4.4 Chapter 4 Summary and Review
Chapter 4 Review Problems
1. \(12^{\circ}\)
3.
a \(150^{\circ}, -210^{\circ}\)
b \(240^{\circ},-120^{\circ}\)
c \(160^{\circ},-560^{\circ}\)
d \(20^{\circ},-340^{\circ}\)
5.
a \(I, 60^{\circ} ; 120^{\circ}, 240^{\circ}, 300^{\circ}\)
b \(I V, 25^{\circ} ; 155^{\circ}, 205^{\circ}, 335^{\circ}\)
c \(I I, 80^{\circ} ; 80^{\circ}, 260^{\circ}, 280^{\circ}\)
d \(I I I, 70^{\circ} ; 70^{\circ}, 110^{\circ}, 290^{\circ}\)
7.
a
| \(\theta\) | \(30^{\circ}\) | \(60^{\circ}\) | \(90^{\circ}\) | \(120^{\circ}\) | \(150^{\circ}\) | \(180^{\circ}\) | \(210^{\circ}\) | \(240^{\circ}\) | \(270^{\circ}\) | \(300^{\circ}\) | \(330^{\circ}\) | \(360^{\circ}\) |
| \(f(\theta)\) | 30 | 60 | 90 | 60 | 30 | 0 | 30 | 60 | 90 | 60 | 30 | 0 |
b 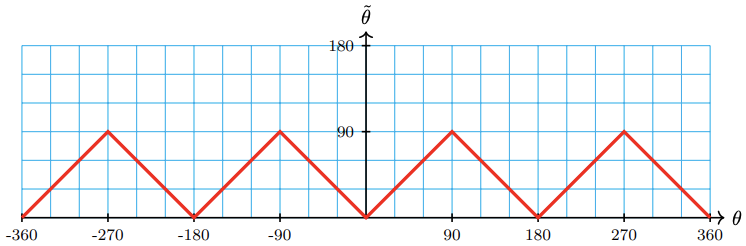
9. \(210^{\circ}, 330^{\circ}\)
11. \(120^{\circ}, 240^{\circ}\)
13. \(45^{\circ}, 225^{\circ}\)
15. \(23^{\circ}, 337^{\circ}\)
17. \(72^{\circ}, 252^{\circ}\)
19. \(163^{\circ}, 277^{\circ}\)
21. \(221.81^{\circ}, 318.19^{\circ}\)
23. \(123.69^{\circ}, 303.69^{\circ}\)
25. \(128.68^{\circ}, 231.32^{\circ}\)
27. (−9.74, −2.25)
29. (−0.28, 8.00)
31. (2.84, 0.98)
33. south: 1.74 mi, west: 9.85 mi
35. \(y=4+7 \sin (180 \theta)\)
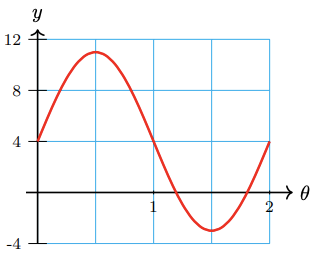
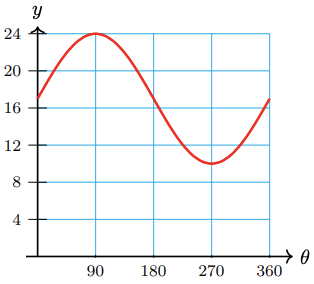
37. \(y=17+7 \sin \theta\)
39. \(\dfrac{\sqrt{3}}{2}\)
41. 0
43. \(y=1.5 \cos \left(\dfrac{\theta}{3}\right), M\left(-90^{\circ}, \dfrac{3 \sqrt{3}}{4}\right), N\left(180^{\circ}, \dfrac{3}{4}\right)\)
45. \(y=3+3 \sin 2 \theta, A\left(-45^{\circ}, 6\right), B\left(120^{\circ}, 3-\dfrac{3 \sqrt{3}}{2}\right)\)
47.
a 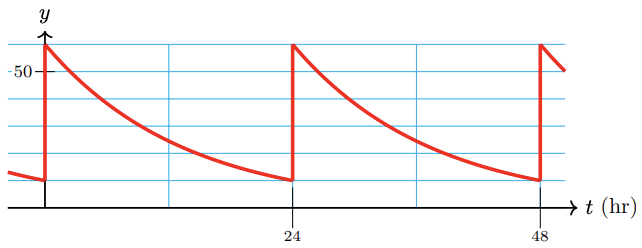
b 24 hours
49.
a 
b 20 sec
51.
a 
b amp: 2, period: \(360^{\circ}\), midline: \(y = 4\)
53.
a 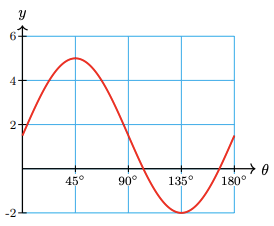
b amp: 3.5, period: \(180^{\circ}\), midline: \(y = 1.5\)
55. \(30^{\circ}\)
57. \(92.05^{\circ}\)
59. \(y = x + 2\)
61. \(y = - \sqrt{3}x + 3 \sqrt{3} - 4\)
63.
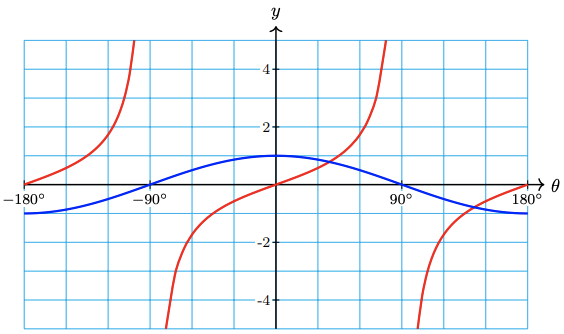
The \(\theta\)-intercepts of \(\cos \theta\) occur at the vertical asymptotes of \(\tan \theta\).


