2.4E: Infinite Limits EXERCISES
- Page ID
- 32764
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In the following exercises, find the limit.
In the following exercises, consider the graph of the function \(y=f(x)\) shown here. Which of the statements about \(y=f(x)\) are true and which are false? Explain why a statement is false.
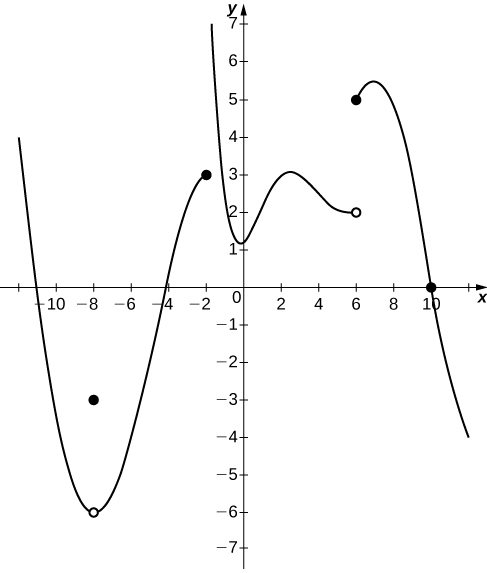
J46) \(\displaystyle \lim_{x→10}f(x)=0\)
J47) \(\displaystyle \lim_{x→−2^+}f(x)=3\)
- Answer:
-
False; \(\displaystyle \lim_{x→−2^+}f(x)=+∞\)
J48) \(\displaystyle \lim_{x→−8}f(x)=f(−8)\)
J49) \(\displaystyle \lim_{x→6}f(x)=5\)
- Answer:
-
False; \(\displaystyle \lim_{x→6}f(x)\) DNE since\(\displaystyle \lim_{x→6^−}f(x)=2\) and \(\displaystyle \lim_{x→6^+}f(x)=5\).
J2.4.1)
a. \(\displaystyle \lim_{x→−3^+}\frac{x}{x+3}\)
b. \(\displaystyle \lim_{x→−3^-}\frac{x}{x+3}\)
c. \(\displaystyle \lim_{x→−3}\frac{x}{x+3}\)
- Answer:
- a. −∞
b. ∞
c. DNE
J2.4.2) \(\displaystyle \lim_{x→0}\ln |x|\)
J2.4.3)
a. \(\displaystyle \lim_{x→5^+}\frac{2}{x-5}\)
b. \(\displaystyle \lim_{x→5^-}\frac{2}{x-5}\)
c. \(\displaystyle \lim_{x→5}\frac{2}{x-5}\)
- Answer:
- a. ∞
b. −∞
c. DNE
J2.4.4)
a. \(\displaystyle \lim_{x→-2^+}\frac{x}{(x+2)^2}\)
b. \(\displaystyle \lim_{x→-2^-}\frac{x}{(x+2)^2}\)
c. \(\displaystyle \lim_{x→-2}\frac{x}{(x+2)^2}\)
J2.4.5)
a. \(\displaystyle \lim_{x→6^+}\frac{x}{(6-x)^2}\)
b. \(\displaystyle \lim_{x→6^-}\frac{x}{(6-x)^2}\)
c. \(\displaystyle \lim_{x→6}\frac{x}{(6-x)^2}\)
- Answer:
- a. ∞
b. ∞
c. ∞
J2.4.6)
a. \(\displaystyle \lim_{x→1^+}\frac{2x^2+7x−4}{x^2+x−2}\)
b. \(\displaystyle \lim_{x→1^−}\frac{2x^2+7x−4}{x^2+x−2}\)
c.\(\displaystyle \lim_{x→1}\frac{2x^2+7x−4}{x^2+x−2}\)
J2.4.7) \(\displaystyle \lim_{x→1}\frac{x^3−1}{x^2−1}\)
- Answer:
- \(\displaystyle lim_{x→1}\frac{x^3−1}{x^2−1}=\displaystyle \lim_{x→1}\frac{(x-1)(x^2+x+1)}{(x-1)(x+1)}=\displaystyle \lim_{x→1}\frac{x^2+x+1}{x+1}=\frac{3}{2}\)
J2.4.8) \(\displaystyle \lim_{x→1/2}\frac{2x}{2x−1}\)
J2.4.9) \(\displaystyle \lim_{x→1/2}\frac{2x^2+3x−2}{2x−1}\)
- Answer:
- \(\displaystyle \lim_{x→ 1/2}\frac{2x^2+3x−2}{2x−1}=\displaystyle \lim_{x→1/2}\frac{(2x−1)(x+2)}{2x−1}=\displaystyle \lim_{x→1/2}(x+2)=\frac{5}{2}\)
State the vertical asymptote for each function, if any.
J2.4.10) \(f(x)=\ln x\)
J2.4.11) \(g(x)=\frac{x+5}{x-4}\)
- Answer:
- \(x=4\)
J2.4.12) \(g(x)=\frac{7}{x+5}\)
J2.4.13) \(g(x)=\frac{7}{x}\)
- Answer:
- \(x=0\)
J2.4.14)
a. \(\displaystyle \lim_{x→\frac{\pi}{2}^+}\tan x=\)
b. \(\displaystyle \lim_{x→\frac{\pi}{2}^-}\tan x=\)
c. \(\displaystyle \lim_{x→\frac{\pi}{2}}\tan x=\)
d. Does \(f(x)=\tan x\) have a vertical asymptote at \(x=\frac{\pi}{2}\)?