2.5E: Limits at Infinity EXERCISES

Last updated
Save as PDF

Page ID: 32766

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

2.5E: Limits at Infinity EXERCISES

For the following exercises, examine the graphs. Identify where the vertical asymptotes are located.

251)

Answer:: $x=1$

252)

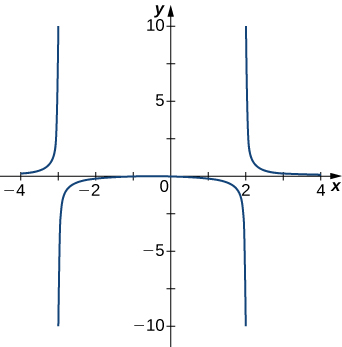
$CNX_Calc_Figure_04_06_202.jpeg$

253)

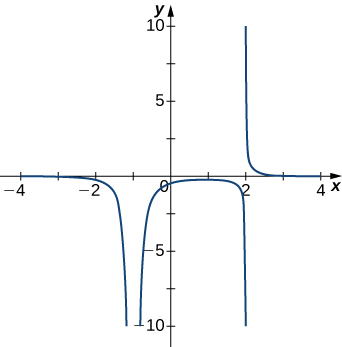
$CNX_Calc_Figure_04_06_203.jpeg$

Answer:: $x=−1,x=2$

254)

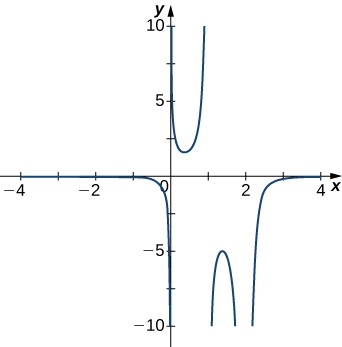
$CNX_Calc_Figure_04_06_204.jpeg$

255)

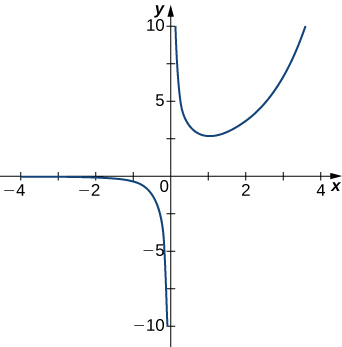
$CNX_Calc_Figure_04_06_205.jpeg$

Answer:: $x=0$

For the following functions $f(x)$, determine whether there is an asymptote at $x=a$. Justify your answer without graphing on a calculator.

256) $f(x)=\frac{x+1}{x^2+5x+4},a=−1$

257) $f(x)=\frac{x}{x−2},a=2$

Answer:: Yes, there is a vertical asymptote

258) $f(x)=(x+2)^{3/2},a=−2$

259) $f(x)=(x−1)^{−1/3},a=1$

Answer:: Yes, there is vertical asymptote

260) $f(x)=1+x^{−2/5},a=1$

For the following exercises, evaluate the limit.

261) $\displaystyle \lim_{x→∞}\frac{1}{3x+6}$

Answer:: $0$

262) $\displaystyle \lim_{x→∞}\frac{2x−5}{4x}$

263) $\displaystyle \lim_{x→∞}\frac{x^2−2x+5}{x+2}$

Answer:: $∞$

264) $\displaystyle \lim_{x→−∞}\frac{3x^3−2x}{x^2+2x+8}$

265) $\displaystyle \lim_{x→−∞}\frac{x^4−4x^3+1}{2−2x^2−7x^4}$

Answer:: $−\frac{1}{7}$

266) $\displaystyle \lim_{x→∞}\frac{3x}{\sqrt{x^2+1}}$

267) $\displaystyle \lim_{x→−∞}\frac{\sqrt{4x^2−1}}{x+2}$

Answer:: $−2$

268) $\displaystyle \lim_{x→∞}\frac{4x}{\sqrt{x^2−1}}$

269) $\displaystyle \lim_{x→−∞}\frac{4x}{\sqrt{x^2−1}}$

Answer:: $−4$

270) $\displaystyle \lim_{x→∞}\frac{2\sqrt{x}}{x−\sqrt{x}+1}$

For the following exercises, find the horizontal and vertical asymptotes.

271) $f(x)=x−\frac{9}{x}$

Answer:: Horizontal: none, vertical: $x=0$

272) $f(x)=\frac{1}{1−x^2}$

273) $f(x)=\frac{x^3}{4−x^2}$

Answer:: Horizontal: none, vertical: $x=±2$

274) $f(x)=\frac{x^2+3}{x^2+1}$

275) $f(x)=sin(x)sin(2x)$

Answer:: Horizontal: none, vertical: none

276) $f(x)=cosx+cos(3x)+cos(5x)$

277) $f(x)=\frac{xsin(x)}{x^2−1}$

Answer:: Horizontal: $y=0,$ vertical: $x=±1$

278) $f(x)=\frac{x}{sin(x)}$

279) $f(x)=\frac{1}{x^3+x^2}$

Answer:: Horizontal: $y=0,$ vertical: $x=0$ and $x=−1$

280) $f(x)=\frac{1}{x−1}−2x$

281) $f(x)=\frac{x^3+1}{x^3−1}$

Answer:: Horizontal: $y=1,$ vertical: $x=1$

282) $f(x)=\frac{sinx+cosx}{sinx−cosx}$

283) $f(x)=x−sinx$

Answer:: Horizontal: none, vertical: none

284) $f(x)=\frac{1}{x}−\sqrt{x}$

For the following exercises, construct a function $f(x)$ that has the given asymptotes.

285) $x=1$ and $y=2$

Answer:: Answers will vary, for example: $y=\frac{2x}{x−1}$

286) $x=1$ and $y=0$

287) $y=4, x=−1$

Answer:: Answers will vary, for example: $y=\frac{4x}{x+1}$

288) $x=0$

CHAPTER REVIEW EXERCISES

CR 1) $\displaystyle \lim_{x→∞}\frac{3x\sqrt{x^2+1}}{\sqrt{x^4−1}}$

Answer:: $3$

CR 2) $\displaystyle \lim_{x→∞}cos(\frac{1}{x})$

CR 3) $\displaystyle \lim_{x→1}\frac{x−1}{sin(πx)}$

Answer:: $−\frac{1}{π}$

CR 4) $\displaystyle \lim_{x→∞}(3x)^{1/x}$

Search

Text Color

Text Size

Margin Size

Font Type

2.5E: Limits at Infinity EXERCISES