7.3: Appendix C

Last updated
Save as PDF

Page ID: 51019

Amy Lagusker
College of the Canyons

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Solutions for Partner Activities

Chapter 2

Section 2.3

Partner Activity 1

Step 1: Add up both lengths to find the total length

\[2 \dfrac{3}{4}+1 \dfrac{1}{2}=\dfrac{11}{4}+\dfrac{3}{2}=\dfrac{11}{4}+\dfrac{6}{4}=\dfrac{17}{4}=4 \dfrac{1}{4} \nonumber \]

Step 2: Divide the part by the whole

\[\dfrac{\text {Sam}}{\text {Total}}=\dfrac{2 \dfrac{3}{4}}{4 \dfrac{1}{4}}=2 \dfrac{3}{4} \div 4 \dfrac{1}{4}=\dfrac{11}{4} \div \dfrac{17}{4}=\dfrac{11}{4} \times \dfrac{4}{17}=\dfrac{11}{17} \approx 0.65=65 \% \approx \dfrac{2}{3} \nonumber \]

Partner Activity 2

\[\begin{array}{l}
\dfrac{1 \text { hour }}{84 \text { miles }+92 \text { miles }}=\dfrac{1 \text { hour }}{176 \text { miles }} \\
\rightarrow \dfrac{132 \text { miles needed in one hour }}{176 \text { miles total in one hour }}=\dfrac{3}{4} \text { hour }=45 \text { minutes }
\end{array} \nonumber \]

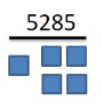
Partner Activity 3

$clipboard_ed5d202eb0ef532348c31d511d42f97ae.png$ $\begin{array}{c}
\rightarrow 5285 \div 5=1057=\text { first number } \\
1057 \times 4=4228=\text { second number } \\
\text { Check it! } 1057+4228=5285
\end{array} $

Section 2.4

Partner Activity 1

MMXLV = 1000+1000+(50-10)+5 = 2045
MDCCLXXXIX = 1000+500+200+50+30+(10-1) = 1789
1993 = 1000+(1000-100)+(100-10)+1+1+1 = MCMXCIII
5495 = 5000+(500-100)+(100-10)+5 = VCDXCV

Section 2.6

Partner Activity 1

1. $132_{\text {four}}$
2. $200313_{\text {four}}$
3. $100_{\text {four}}$
1. 15
2. 278
3. Undefined

Section 2.8

Partner Activity 1

$116_{\text {nine}}$
$1030_{\text {four}}$
$513_{\text {six}}$
$21_{\text {three}}$
$111110_{\text {two}}$

Chapter 3

Section 3.2

Partner Activity 1

Answer: 265

Partner Activity 2

Answers vary

Partner Activity 3

Section 3.4

Partner Activity 1

\[\begin{array}{l}
5 \div 0=\text { undefined } \\
0 \div 5=0 \\
0 \div 0=\text { indeterminate }
\end{array} \nonumber \]

We know that $18 \div 6=3$ because $3 \times 6=18$, therefore. Using a similar approach, we know that $5 \div 0 \neq 0$, since $0 \times 0 \neq 5$

Section 3.5

Partner Activity 1

$14.47
$3.65
$16.32

Partner Activity 2

$12 \times 6 = 72$
$10 \times 18 = 180$
$8 \times 8 = 64$

Partner Activity 3

321
229
15453

Section 3.6

Partner Activity 1

Answers vary. Samples are below:

Here to Baker, CA
The length of my bedroom
The weight of a 2nd grader

Section 3.7

Partner Activity 1

309.26
92.86%
114.06

Chapter 4

Section 4.2

Partner Activity 1

The denominator is VERY MUCH less than the numerator, i.e. $\dfrac{1}{10000}$
Both the denominator and the numerator are large numbers and they are very close in distance, i.e. $\dfrac{999}{1000}$
The numerator is roughly half of the denominator, i.e. $\dfrac{15}{31}$
The numerator is roughly a third of the denominator, i.e. $\dfrac{21}{60}$

Partner Activity 2

\[\dfrac{3}{8} \rightarrow \dfrac{1}{2}, \dfrac{5}{4} \rightarrow 1, \dfrac{2}{9} \rightarrow 0, \dfrac{4}{7} \rightarrow \dfrac{1}{2}, \dfrac{1}{3} \rightarrow \frac{1}{2} \nonumber \]

Section 4.3

Partner Activity 1

\[\dfrac{51}{684}+\dfrac{43}{684}+\dfrac{738}{684}=\dfrac{832}{684} \nonumber\]

\[\dfrac{1}{8}+\dfrac{4}{5}+\dfrac{1}{9}=\dfrac{1}{360}+\dfrac{ }{360}+\dfrac{ }{360}= \dfrac{45}{360}+\dfrac{288}{360}+\dfrac{40}{360}=\dfrac{373}{360} \nonumber \]

Partner Activity 2

Division works. The rest do not.

Chapter 5

Section 5.2

Partner Activity 1

Factors: 1, 2, 3, 5, 6, 10, 15, 30

First four multiples: 30, 60, 90, 120

Partner Activity 2

Primes: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and 97

Partner Activity 3

0, 1, negative = neither. 2 is the first prime number.

Partner Activity 4

$85=5 \cdot 17$
$350=2 \cdot 5^{2} \cdot 7$
$60=2^{2} \cdot 3 \cdot 5$

Section 5.4

Partner Activity 1

2 feet; The GCF of (6, 8, 12) = 2

Partner Activity 2

Each packet contains 12 cards; The GCF of (24, 60, 48) = 12

Section 5.5

Partner Activity 1

120 cookies; The LCM of (15, 24) = 120

Partner Activity 2

$\dfrac{1}{12}$
$\dfrac{1}{6}$
14

Chapter 6

Section 6.2

Partner Activity 1

$clipboard_e16301d31a71f88c6aa04060facf19713.png$
$clipboard_e2d617da3db818022a989bf2a6bc18d01.png$
Does not exist

Partner Activity 2

A square is a rectangle
Parallelogram
A regular has all same sides and all same angles

Partner Activity 3

180
540
2340
360

Partner Activity 4

Section 6.3

Partner Activity 1

Area is base times height, two dimensions
Volume is base times height times width, three dimensions

Partner Activity 2

About $12 \text { units}^2$

Partner Activity 3

$52 \text { units}^2$

Partner Activity 4

$24 \text { units}^3$

Section 6.4

Partner Activity 1

$\dfrac{5}{9}$ yards
84480 feet

Section 6.5

Partner Activity 1

$1200 \text { inches}^2$
$225 \text { feet}^2$
$196838560.5 \text { miles}^2$
$37.68 \text { inches}^3$

Search

Text Color

Text Size

Margin Size

Font Type