11.5: Graphing with Intercepts (Part 1)
- Last updated
- Jul 2, 2019
- Save as PDF
- Page ID
- 21784
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
- Identify the intercepts on a graph
- Find the intercepts from an equation of a line
- Graph a line using the intercepts
- Choose the most convenient method to graph a line
be prepared!
Before you get started, take this readiness quiz.
- Solve: 3x + 4y = −12 for x when y = 0. If you missed this problem, review Example 9.11.6.
- Is the point (0, −5) on the x-axis or y-axis? If you missed this problem, review Example 11.1.5.
- Which ordered pairs are solutions to the equation 2x − y = 6? (a) (6, 0) (b) (0, −6) (c) (4, −2). If you missed this problem, review Example 11.2.8.
Identify the Intercepts on a Graph
Every linear equation has a unique line that represents all the solutions of the equation. When graphing a line by plotting points, each person who graphs the line can choose any three points, so two people graphing the line might use different sets of points.
At first glance, their two lines might appear different since they would have different points labeled. But if all the work was done correctly, the lines will be exactly the same line. One way to recognize that they are indeed the same line is to focus on where the line crosses the axes. Each of these points is called an intercept of the line.
Definition: Intercepts of a Line
Each of the points at which a line crosses the x-axis and the y-axis is called an intercept of the line.
Let’s look at the graph of the lines shown in Figure 11.5.1.
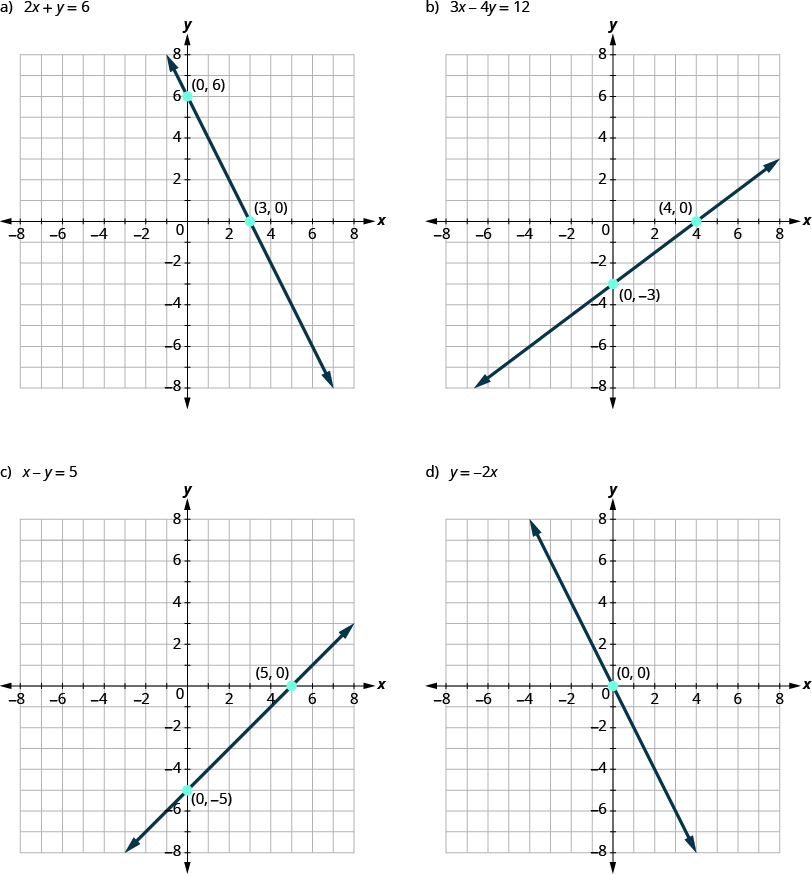
Figure 11.5.1
First, notice where each of these lines crosses the x- axis:
| Figure: | The line crosses the x-axis at: | Ordered pair of this point |
|---|---|---|
| Figure 11.5.1a | 3 | (3,0) |
| Figure 11.5.1b | 4 | (4,0) |
| Figure 11.5.1c | 5 | (5,0) |
| Figure 11.5.1d | 0 | (0,0) |
Do you see a pattern?
For each row, the y-coordinate of the point where the line crosses the x-axis is zero. The point where the line crosses the x-axis has the form (a, 0); and is called the x-intercept of the line. The x-intercept occurs when y is zero.
Now, let's look at the points where these lines cross the y-axis.
| Figure: | The line crosses the x-axis at: | Ordered pair of this point |
|---|---|---|
| Figure 11.5.1a | 6 | (0, 6) |
| Figure 11.5.1b | -3 | (0, -3) |
| Figure 11.5.1c | -5 | (0, -5) |
| Figure 11.5.1d | 0 | (0, 0) |
Definition: x-intercept and y-intercept of a line
The x-intercept is the point, (a, 0), where the graph crosses the x-axis.
The x-intercept occurs when y is zero.
The y-intercept is the point, (0, b), where the graph crosses the y-axis.
The y-intercept occurs when x is zero.
Example 11.5.1
Find the x- and y-intercepts of each line:
(a) x + 2y = 4
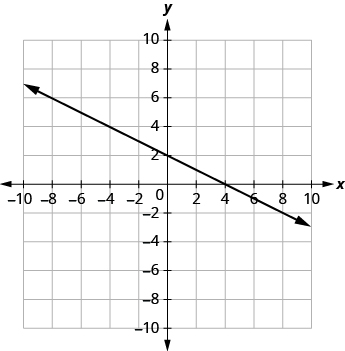
(b) 3x - y = 6
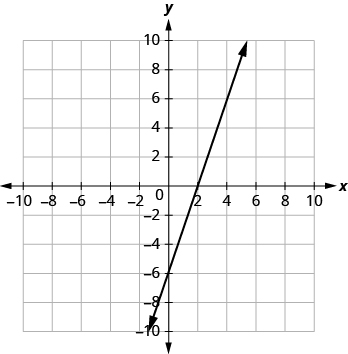
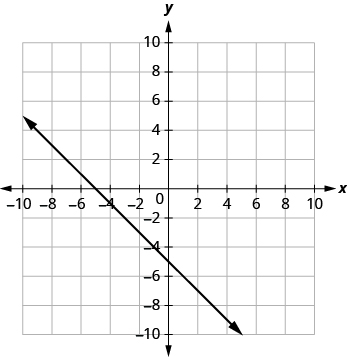
(c) x + y = -5
Solution
(a)
| The graph crosses the x-axis at the point (4, 0). | The x-intercept is (4, 0). |
| The graph crosses the y-axis at the point (0, 2). | The x-intercept is (0, 2). |
(b)
| The graph crosses the x-axis at the point (2, 0). | The x-intercept is (2, 0). |
| The graph crosses the y-axis at the point (0, -6). | The x-intercept is (0, -6). |
(c)
| The graph crosses the x-axis at the point (-5, 0). | The x-intercept is (-5, 0). |
| The graph crosses the y-axis at the point (0, -5). | The x-intercept is (0, -5). |
Exercise 11.5.1A
Find the x- and y-intercepts of the graph: x − y = 2.
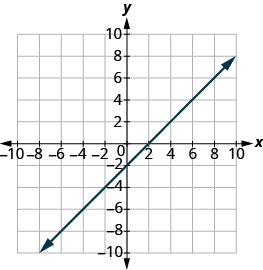
- Answer
-
x-intercept (2,0); y-intercept (0,-2)
Exercise 11.5.1B
Find the x- and y-intercepts of the graph: 2x + 3y = 6.
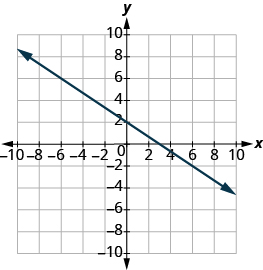
- Answer
-
x-intercept (3,0); y-intercept (0,2)
Find the Intercepts from an Equation of a Line
Recognizing that the x-intercept occurs when y is zero and that the y-intercept occurs when x is zero gives us a method to find the intercepts of a line from its equation. To find the x-intercept, let y = 0 and solve for x. To find the y-intercept, let x = 0 and solve for y.
Definition: Find the x and y from the Equation of a Line
Use the equation to find:
- the x-intercept of the line, let y = 0 and solve for x.
- the y-intercept of the line, let x = 0 and solve for y
| x | y |
|---|---|
| 0 | |
| 0 |
Example 11.5.2
Find the intercepts of 2x + y = 6
Solution
We'll fill in Figure 11.5.2.
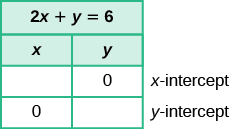
Figure 11.5.2
To find the x- intercept, let y = 0:
| Substitute 0 for y. | 2x+0=6 |
| Add. | 2x = 6 |
| Divide by 2. | x = 3 |
The x-intercept is (3, 0).
To find the y- intercept, let x = 0:
| Substitute 0 for x. | 2⋅0+y=6 |
| Multiply. | 0 + y = 6 |
| Add. | y = 6 |
The y-intercept is (0, 6).
| 2x + y = 6 | |
|---|---|
| x | y |
| 3 | 0 |
| 0 | 6 |
Figure 11.5.3
The intercepts are the points (3, 0) and (0, 6).
Exercise 11.5.2A
Find the intercepts: 3x + y = 12.
- Answer
-
x-intercept (4,0); y-intercept (0,12)
Exercise 11.5.2B
Find the intercepts: x + 4y = 8.
- Answer
-
x-intercept (8,0); y-intercept (0,2)
Example 11.5.3
Find the intercepts of 4x−3y = 12.
Solution
To find the x-intercept, let y = 0.
| Substitute 0 for y. | 4x − 3 • 0 = 12 |
| Multiply. | 4x − 0 = 12 |
| Subtract. | 4x = 12 |
| Divide by 4. | x = 3 |
The y-intercept is (0, −4). The intercepts are the points (−3, 0) and (0, −4).
| 4x - 3y = 12 | |
|---|---|
| x | y |
| 3 | 0 |
| 0 | -4 |
Exercise 11.5.3A
Find the intercepts of the line: 3x−4y = 12.
- Answer
-
x-intercept (4,0); y-intercept (0,-3)
Exercise 11.5.3B
Find the intercepts of the line: 2x−4y = 8.
- Answer
-
x-intercept (4,0); y-intercept (0,-2)
Graph a Line Using the Intercepts
To graph a linear equation by plotting points, you can use the intercepts as two of your three points. Find the two intercepts, and then a third point to ensure accuracy, and draw the line. This method is often the quickest way to graph a line.
Example 11.5.4
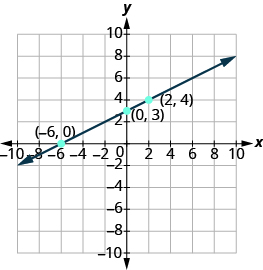
Graph −x + 2y = 6 using intercepts.
Solution
First, find the x-intercept. Let y = 0,
−x+2y=6−x+2(0)=6−x=6x=−6
The x-intercept is (–6, 0).
Now find the y-intercept. Let x = 0.
−x+2y=6−0+2y=62y=6y=3
The y-intercept is (0, 3).
Find a third point. We’ll use x = 2,
−x+2y=6−2+2y=62y=8y=4
A third solution to the equation is (2, 4).
Summarize the three points in a table and then plot them on a graph.
| -x + 2y = 6 | ||
|---|---|---|
| x | y | (x,y) |
| -6 | 0 | (−6, 0) |
| 0 | 3 | (0, 3) |
| 2 | 4 | (2, 4) |
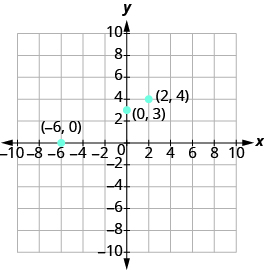
Do the points line up? Yes, so draw line through the points.
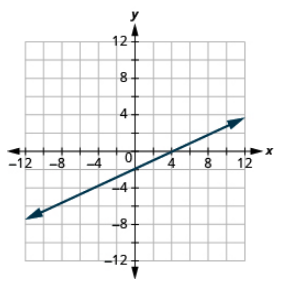
Exercise 11.5.4A
Graph the line using the intercepts: x−2y = 4.
- Answer
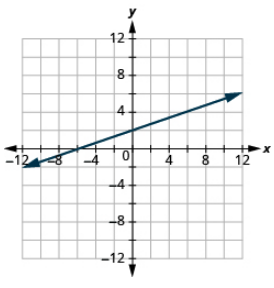
Exercise 11.5.4B
Graph the line using the intercepts: −x + 3y = 6.
- Answer
-
HOW TO: GRAPH A LINE USING THE INTERCEPTS
Step 1. Find the x - and y-intercepts of the line.
- Let y = 0 and solve for x.
- Let x = 0 and solve for y.
Step 2. Find a third solution to the equation.
Step 3. Plot the three points and then check that they line up.
Step 4. Draw the line.
Example 11.5.5
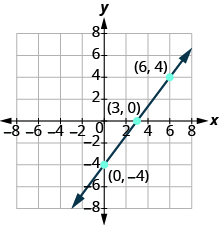
Graph 4x−3y = 12 using intercepts.
Solution
Find the intercepts and a third point.
| x−intercept,lety=04x−3y=124x−3(0)=124x=12x=3 | y−intercept,letx=04x−3y=124(0)−3y=124x−3(4)=12−3y=12y=−4 | thirdpoint,lety=44x−3y=124x−12=124x=24x=6 |
We list the points and show the graph.
| 4x - 3y = 12 | ||
|---|---|---|
| x | y | (x. y) |
| 3 | 0 | (3, 0) |
| 0 | -4 | (0, −4) |
| 6 | 4 | (6, 4) |
Exercise 11.5.5A
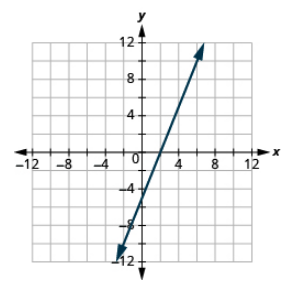
Graph the line using the intercepts: 5x−2y = 10.
- Answer
-
Exercise 11.5.5B
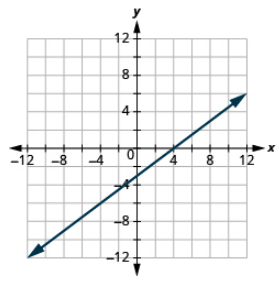
Graph the line using the intercepts: 3x−4y = 12.
- Answer
-
Example 11.5.6
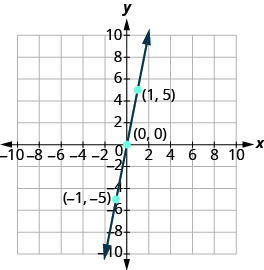
Graph y=5x using the intercepts.
Solution
| x−intercept;Lety=0.y=5x0=5x0=xx=0Thex−interceptis(0,0). | y−intercept;Letx=0.y=5xy=5(0)y=0They−interceptis(0,0). |
This line has only one intercept! It is the point (0, 0).
To ensure accuracy, we need to plot three points. Since the intercepts are the same point, we need two more points to graph the line. As always, we can choose any values for x, so we’ll let x be 1 and −1.
| x=1y=5xy=5(1)y=5(1,−5) | x=−1y=5xy=5(−1)y=−5(−1,−5) |
Organize the points in a table.
| y = 5x | ||
|---|---|---|
| x | y | (x, y) |
| 0 | 0 | (0, 0) |
| 1 | 5 | (1, 5) |
| -1 | -5 | (−1, −5) |
Plot the three points, check that they line up, and draw the line.
Exercise 11.5.6A
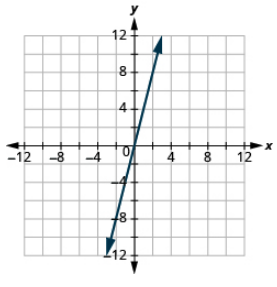
Graph using the intercepts: y=3x.
- Answer
-
Exercise 11.5.6B
Graph using the intercepts: y=−x.
- Answer
-
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


