4.2: Quadratic Functions

Learning Objectives

• Recognize characteristics of parabolas.
• Understand how the graph of a parabola is related to its quadratic function.
• Determine a quadratic function’s minimum or maximum value.
• Solve problems involving a quadratic function’s minimum or maximum value.

Are You Ready?

Try these questions prior to beginning this section to help determine if you are set up for success:

1. Simplify:
   1. \(\quad \sqrt{-9}\)
   2. \(\quad \sqrt{-24}\)
2. Solve:
   1. \(\quad 7h^2+15=26h\)
   2. \(\quad 3y^2-10=0\)
   3. \(\quad 4x^2+7=5x\)

Answer

1. 1. \(\quad 3i\)
   2. \(\quad 2i\sqrt{6}\)

If you missed this problem or feel you could use more practice, review [2.23: Complex Numbers]

2. 1. \(\quad h=3, \dfrac{5}{7}\)
   2. \(\quad y=\pm\dfrac{\sqrt{30}}{3}\)
   3. \(\quad x=\dfrac{5\pm i\sqrt{87}}{8}\)

If you missed this problem or feel you could use more practice, review [2.8: Solving Polynomial Equations, 2.24: Solving Quadratic Equations Using the Square Root Property, 2.25: Solving Quadratic Equations by Completing the Square, and 2.26: Solving Quadratic Equations Using the Quadratic Formula]

Curved antennas, such as the ones shown in Figure \(\PageIndex{1}\), are commonly used to focus microwaves and radio waves to transmit television and telephone signals, as well as satellite and spacecraft communication. The shape used in many antenna and satellite designs are called paraboloids which are studied in multivariable calculus. The cross-section of the antenna is in the shape of a parabola, which can be described by a quadratic function.

Figure \(\PageIndex{1}\): An array of satellite dishes. (credit: Matthew Colvin de Valle, Flickr)

In this section, we will investigate quadratic functions, which frequently model problems involving area and projectile motion. Working with quadratic functions can be less complex than working with higher degree functions, so they provide a good opportunity for a detailed study of function behavior.

Characteristics of Parabolas

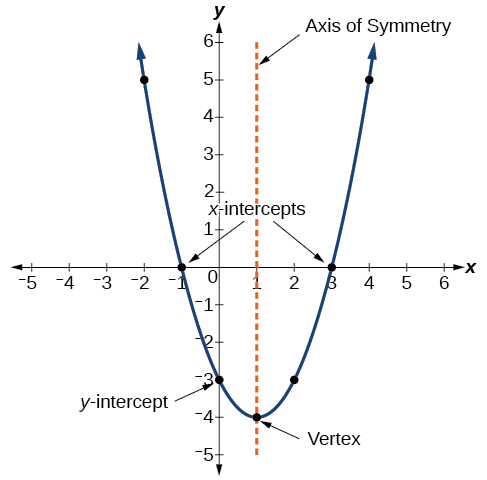
The graph of a quadratic function is a U-shaped curve called a parabola. One important feature of the graph is that it has a local extrema point, called the vertex. If the parabola opens up, the vertex represents the lowest point on the graph, or the minimum value of the quadratic function. If the parabola opens down, the vertex represents the highest point on the graph, or the maximum value. In either case, the vertex is a turning point on the graph. The graph is also symmetric with a vertical line drawn through the vertex, called the axis of symmetry. The y-intercept is the point at which the parabola crosses the \(y\)-axis. The x-intercepts are the points at which the parabola crosses the \(x\)-axis. These features are illustrated in Figure \(\PageIndex{2}\).

Figure \(\PageIndex{2}\): Graph of a parabola showing where the \(x\) and \(y\) intercepts, vertex, and axis of symmetry are.

Example \(\PageIndex{1}\)

Determine the vertex, axis of symmetry, x-intercepts, and y-intercept of the parabola shown in Figure \(\PageIndex{3}\).

Figure \(\PageIndex{3}\).

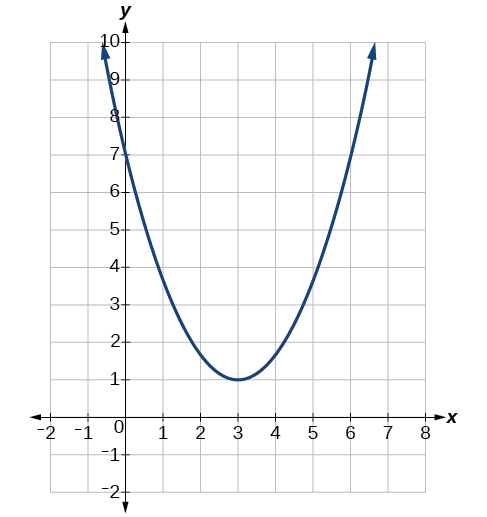
Solution

The vertex is the lowest point of the graph. We can see that the vertex is at \((3,1)\). The axis of symmetry is the vertical line that intersects the parabola at the vertex. So the axis of symmetry is \(x=3\). This parabola does not cross the x-axis, so it has no x-intercepts. It crosses the \(y\)-axis at \((0,7)\) so this is the y-intercept.

We have discussed transformations of functions. Given the function \(f(x)=3(x+2)^{2} -13\), we know that the parabola open upward and that the vertex is at \((-2,-13)\). With quadratics we sometimes call this transformation form of the function vertex form.

Now, consider what happens when we expand this function out:

\[\begin{array}{l} {f(x)=3(x+2)^{2} -13} \\ {f(x)=3(x+2)(x+2)-13} \\ {f(x)=3(x^{2} +4x+4)-13} \\ {f(x)=3x^{2} +12x+12)-13} \\{f(x)= 3x^{2} +12x-1}
\end{array} \nonumber \]

This expanded form, \(f(x)= 3x^{2} +12x-1 \), is commonly called general form of a quadratic function. (Note that this terminology is not universal but we will refer to this as general form throughout this text).

Also, notice that the leading coefficient of 3 was the same value in the vertex and general form of the function. This value tells us whether the graph has a vertical stretch or compression as well as an x-axis reflection.

General Form of a Quadratic Function

The general form of a quadratic function is \(f(x)=ax^2+bx+c\) where \(a\), \(b\), and \(c\) are real numbers and \(a{\neq}0\).

• If \(a>0\), then the parabola opens upward.
• If \(a<0\), then the parabola opens downward.

Next, how do we determine what the vertex of a quadratic function is when the function is given in general form? To do so, we rewrite the function in vertex form by completing the square. Let's look at an example of this:

Given the function \(f(x)=x^2+2x+4\), begin by grouping the variable terms together, \[f(x)=(x^2+2x)+4 \nonumber \] Then complete the square by taking half of the linear term coefficient and the squaring it, \((\frac{1}{2}(2))^2=1\). Next, add and subtract this value to the function, \[f(x)=(x^2+2x+1)-1+4 \nonumber \]

Now factor and simplify to get the vertex form, \[f(x)=(x+1)^2+3\nonumber \]

Completing the square is a very useful skill for writing quadratic functions in vertex form. It is also useful for writing many other equations in more useful forms in calculus. Let's look at another example using this important skill.

Example \(\PageIndex{2}\)

Rewrite \(f(x)=2x^{2} -12x+14\) into vertex form by completing the square and identify the vertex.

Solution

We start by factoring the leading coefficient from the quadratic and linear terms.

\[2(x^{2} -6x)+14 \nonumber \]

Take half of the linear coefficient, -6, which is -3, then square to get (-3)\({}^{2}\) = 9. \[(x^{2} -6x+9)=(x-3)^{2} \nonumber \]

Now, we can’t just add 9 into the expression – that would change the value of the expression. In fact, adding 9 inside the parentheses actually adds 18 to the expression, since the 2 outside the parentheses will distribute. To keep the expression balanced, we can subtract 18.

\[2(x^{2} -6x+9)+14-18 \nonumber \]

Simplifying, we are left with vertex form.

\[2(x-3)^{2} -4 \nonumber \]

The vertex is \((3,-4)\).

Vertex Form of a Quadratic Function

The vertex form of a quadratic function is

\[f(x)=a(x-h)^{2} +k \nonumber \]

The vertex of the quadratic function is located at (\(h\), \(k\)), where \(h\) and \(k\) are the numbers in the transformation form of the function.

In the previous example, we saw that it is possible to rewrite a quadratic function in vertex form by completing the square. It would be useful to reverse this process since the vertex form reveals the vertex.

Expanding out the vertex form of a quadratic gives:

\[\begin{array}{l} {f(x)=a(x-h)^{2} +k} \\{f(x)=a(x-h)(x-h)+k} \\ {f(x)=a(x^{2} -2xh+h^{2} +k} \\{f(x)=ax^{2} -2ahx+ah^{2} +k} \end{array}\ \nonumber \]

This is equivalent to the general form of the quadratic:

\[ax^{2} -2ahx+ah^{2} +k=ax^{2} +bx+c\ \nonumber \]

The second degree terms are already equal and have the same labels. For the linear terms to be equal, the coefficients must be equal. So,

\[-2ah=b \nonumber \]

then solving for h we get: \[h=-\dfrac{b}{2a}\ \nonumber \]

Likewise, set the constant terms equal,\[ah^{2} +k=c \nonumber \]

Solving for k we get: \[k=c-ah^{2} =c-a\left(-\dfrac{b}{2a} \right)^{2} =c-a\dfrac{b^{2} }{4a^{2} } =c-\dfrac{b^{2} }{4a}\ \nonumber\]

In practice, though, it is usually easier to remember that \(k\) is the output value of the function when the input is \(h\), so \(k=f(h)\).

Vertex Formula

Given a quadratic function in general form, \(f(x)=ax^2+bx+c\), the vertex is \((h,k)\) where

\(h=-\dfrac{b}{2a}\ \) and \(k=f(h)\)

Example \(\PageIndex{3}\)

Find the vertex of the quadratic \(f(x)=2x^{2} -6x+7\).

Solution

The x-coordinate of the vertex will be at

\[h=-\dfrac{b}{2a} =-\dfrac{-6}{2(2)} =\dfrac{6}{4} =\dfrac{3}{2} \ \nonumber \]

The y-coordinate of the vertex will be at

\[f(\dfrac{3}{2} )=2(\dfrac{3}{2})^{2} -6(\dfrac{3}{2} )+7=\dfrac{5}{2} \ \nonumber \]

The vertex is \(\left(\dfrac{3}{2}, \dfrac{5}{2}\right)\)

Intercept Behavior

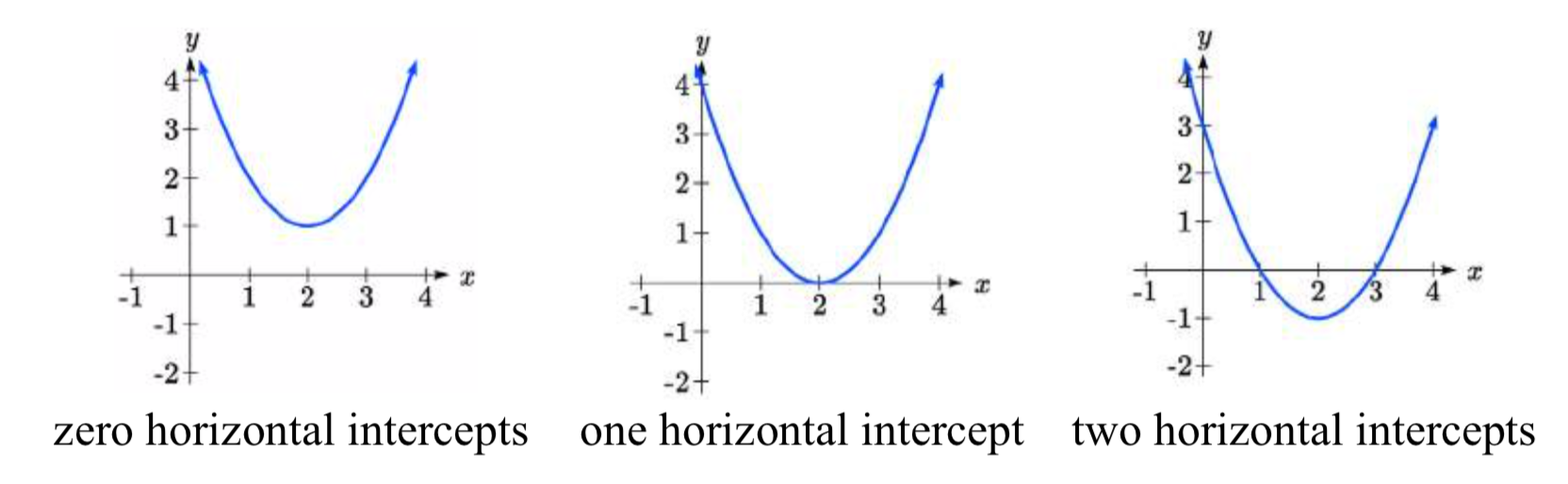
As with any function, we can find the y-intercepts of a quadratic by evaluating the function at an input of zero. All quadratics functions have one y-intercept since the domain is all real numbers. We can find the x-intercepts by solving for when the output will be zero. Notice that depending upon the location of the graph, we might have zero, one, or two horizontal intercepts.

Example \(\PageIndex{4}\)

Find intercepts of the quadratic \(f(x)=3x^{2} +5x-2\)

Solution

We can find the y-intercept by evaluating the function at an input of zero:

\[f(0)=3(0)^{2} +5(0)-2=-2\ \nonumber \] Vertical intercept at (0,-2)

For the x-intercepts, we solve for when the output will be zero

\[0=3x^{2} +5x-2\ \nonumber \]

In this case, the quadratic can be factored easily, providing the simplest method for solution

\[0=(3x-1)(x+2)\ \nonumber \]

\[\begin{array}{l} {0=3x-1} \\[4pt] {x=\dfrac{1}{3} } \end{array} \qquad\text{ or }\qquad\begin{array}{l} {0=x+2} \\[4pt] {x=-2} \end{array}\ \nonumber \]

x-intercepts at \(\left(\dfrac{1}{3} ,0\right)\) and (-2,0)

Notice that in the standard form of a quadratic, the constant term c reveals the vertical intercept of the graph.

Example \(\PageIndex{5}\)

Find the x-intercepts of the quadratic \(f(x)=2x^{2} +4x-4\)

Solution

Again we will solve for when the output will be zero

\[0=2x^{2} +4x-4\ \nonumber \]

Since the quadratic is not easily factorable in this case, we solve for the intercepts by first rewriting the quadratic into transformation form.

\[h=-\dfrac{b}{2a} =-\dfrac{4}{2(2)} =-1\ \ \ k=f(-1)=2(-1)^{2} +4(-1)-4=-6\ \nonumber \]

\[f(x)=2(x+1)^{2} -6\ \nonumber \]

Now we can solve for when the output will be zero

\[\begin{array}{l} {0=2(x+1)^{2} -6} \\ {6=2(x+1)^{2} } \\ {3=(x+1)^{2} } \\ {x+1=\pm \sqrt{3} } \\ {x=-1\pm \sqrt{3} } \end{array}\ \nonumber \]

The graph has x-intercepts at \((-1-\sqrt{3} ,0)\)and \((-1+\sqrt{3} ,0)\)

You Try \(\PageIndex{1}\)

For the function \(g(x)=13+x^{2} -6x\), find the y and x-intercepts.

Answer

The y-intercept at (0, 13), There are no x-intercepts since the vertex is above the \(x\)-axis and the graph opens upwards.

Note that if there are no x-intercepts, it is important to explain how you determined that.

The process for finding the x-intercepts is done commonly enough that sometimes people find it easier to solve the problem once in general and remember the formula for the result, rather than repeating the process each time. Based on our previous work we showed that any quadratic in general form can be written into vertex form as:

\[f(x)=a \left(x+\dfrac{b}{2a} \right)^{2} +c-\dfrac{b^{2} }{4a}\nonumber \]

Solving for the horizontal intercepts using this general equation gives:
\[0=a \left(x+\dfrac{b}{2a} \right)^{2} +c-\dfrac{b^{2} }{4a}\ \nonumber \] start to solve for \(x\) by moving the constants to the other side
\[\dfrac{b^{2} }{4a} -c=a \left(x+\dfrac{b}{2a} \right)^{2}\ \nonumber \] divide both sides by \(a\)
\[\dfrac{b^{2} }{4a^{2} } -\dfrac{c}{a} = \left(x+\dfrac{b}{2a} \right)^{2}\ \nonumber \] find a common denominator to combine fractions
\[\dfrac{b^{2} }{4a^{2} } -\dfrac{4ac}{4a^{2} } =\left(x+\dfrac{b}{2a} \right)^{2}\ \nonumber \] combine the fractions on the left side of the equation
\[\dfrac{b^{2} -4ac}{4a^{2} } =\left(x+\dfrac{b}{2a} \right)^{2}\ \nonumber \] take the square root of both sides
\[\pm \sqrt{\dfrac{b^{2} -4ac}{4a^{2} } } =x+\dfrac{b}{2a}\ \nonumber \] subtract \(b/2a\) from both sides
\[-\dfrac{b}{2a} \pm \dfrac{\sqrt{b^{2} -4ac} }{2a} =x\ \nonumber \] combining the fractions
\[x=\dfrac{-b\pm \sqrt{b^{2} -4ac} }{2a}\ \nonumber \] Notice that this can yield two different answers for \(x\)

Quadratic Formula

For a quadratic function given in standard form \(f(x)=ax^{2} +bx+c\), the quadratic formula gives the horizontal intercepts of the graph of this function.

\[x=\dfrac{-b\pm \sqrt{b^{2} -4ac} }{2a} \nonumber \]

Let's practice a few more examples of applying all the concepts we've learned about quadratics.

Example \(\PageIndex{6}\)

Find the domain and range of \(f(x)=−5x^2+9x−1\).

Solution

As with any quadratic function, the domain is all real numbers.

Because \(a\) is negative, the parabola opens downward and has a maximum value. We need to determine the maximum value. We can begin by finding the x-value of the vertex.

\[\begin{align*} h&=−\dfrac{b}{2a} \\[5pt] &=−\dfrac{9}{2(-5)} \\[5pt] &=\dfrac{9}{10} \end{align*}\nonumber \]

The maximum value is given by \(f(h)\).

\[\begin{align*} f \left(\dfrac{9}{10}\right)&=5\left(\dfrac{9}{10}\right)^2+9\left(\dfrac{9}{10}\right)-1 \\[5pt] &= \dfrac{61}{20}\end{align*}\nonumber \]

Since we know the parabola opens down, we know the range is \(f(x){\leq}\dfrac{61}{20}\), or \(\left(−\infty,\dfrac{61}{20}\right]\).

Example \(\PageIndex{7}\)

A backyard farmer wants to enclose a rectangular space for a new garden within her fenced backyard. She has purchased 80 feet of wire fencing to enclose three sides, and she will use a section of the backyard fence as the fourth side.

1. Find a formula for the area enclosed by the fence if the sides of fencing perpendicular to the existing fence have length \(L\).
2. What dimensions should she make her garden to maximize the enclosed area?

Solution

Let’s use a diagram such as Figure \(\PageIndex{4}\) to record the given information. It is also helpful to introduce a temporary variable, \(W\), to represent the width of the garden and the length of the fence section parallel to the backyard fence.

Figure \(\PageIndex{4}\): Diagram of the garden and the backyard.

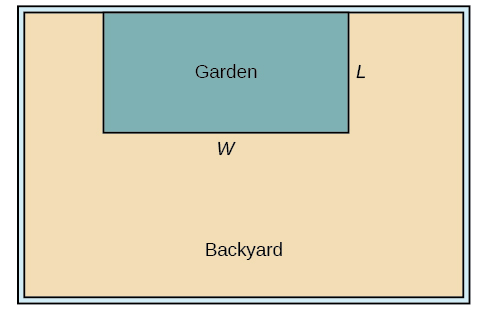
a. We know we have only 80 feet of fence available, and \(L+W+L=80\), or more simply, \(2L+W=80\). This allows us to represent the width, \(W\), in terms of \(L\).

\[W=80−2L\nonumber \]

Now we are ready to write an equation for the area the fence encloses. We know the area of a rectangle is length multiplied by width, so

\[\begin{align*} A&=LW=L(80−2L) \\ A(L)&=80L−2L^2 \end{align*}\nonumber \]

This formula represents the area of the fence in terms of the variable length \(L\). The function, written in general form, is

\[A(L)=−2L^2+80L\nonumber \]

The quadratic has a negative leading coefficient, so the graph will open downward, and the vertex will be the maximum value for the area. In finding the vertex, we must be careful because the equation is not written in standard polynomial form with decreasing powers. This is why we rewrote the function in general form above. Since \(a\) is the coefficient of the squared term, \(a=−2\), \(b=80\), and \(c=0\).

To find the vertex:

\[\begin{align*} h& =−\dfrac{80}{2(−2)} \\ &=20 \end{align*}\nonumber \]

and
\[\begin{align*}k&=A(20) \\ &=80(20)−2(20)^2 \\ &=800 \end{align*}\nonumber \]

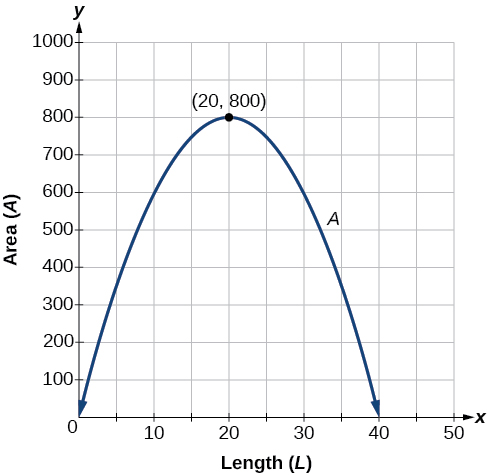
The maximum value of the function is an area of 800 square feet, which occurs when \(L=20\) feet. When the shorter sides are 20 feet, there is 40 feet of fencing left for the longer side. To maximize the area, she should enclose the garden so the two shorter sides have length 20 feet and the longer side parallel to the existing fence has length 40 feet.

Analysis

This problem also could be solved by graphing the quadratic function. We can see where the maximum area occurs on a graph of the quadratic function in Figure \(\PageIndex{5}\).

Figure \(\PageIndex{5}\): Graph of the parabolic function \(A(L)=-2L^2+80L\)

Example \(\PageIndex{8}\)

A ball is thrown upwards from the top of a 40-foot-tall building at a speed of 80 feet per second. The ball’s height above ground can be modeled by the equation \(H(t)=-16t^{2} +80t+40\).

What is the maximum height of the ball?

When does the ball hit the ground? Round to the nearest thousandth.

Solution

To find the maximum height of the ball, we would need to know the vertex of the quadratic.

\[h=-\dfrac{80}{2(-16)} =\dfrac{80}{32} =\dfrac{5}{2} , k=H\left(\dfrac{5}{2} \right)=-16\left(\dfrac{5}{2} \right)^{2} +80\left(\dfrac{5}{2} \right)+40=140\ \nonumber \]

The ball reaches a maximum height of 140 feet after 2.5 seconds.

To find when the ball hits the ground, we need to determine when the height is zero – when \(H(t) = 0\). While we could do this using the transformation form of the quadratic, we can also use the quadratic formula:

\[t=\dfrac{-80\pm \sqrt{80^{2} -4(-16)(40)} }{2(-16)} =\dfrac{-80\pm \sqrt{8960} }{-32}\ \nonumber \]

Since the square root does not simplify nicely, we can use a calculator to approximate the values of the solutions:

\[t=\dfrac{-80-\sqrt{8960} }{-32} \approx 5.458\text{ or }t=\dfrac{-80+\sqrt{8960} }{-32} \approx -0.458\ \nonumber \]

The second answer is outside the reasonable domain of our model, so we conclude the ball will hit the ground after about 5.458 seconds.