7.6: Polygons
- Last updated
- Sep 30, 2020
- Save as PDF
- Page ID
- 51929

- Amy Lagusker
- College of the Canyons
( \newcommand{\kernel}{\mathrm{null}\,}\)
Below is a table of polygons. There are an infinite amount of polygons, but the following are the shapes taught in elementary school.
|
Number of Sides |
Name |
Irregular Polygon |
Regular Polygon |
|---|---|---|---|
|
3 sides |
Triangle |
 |
 |
|
4 sides |
Quadrilateral |
 |
 |
|
5 sides |
Pentagon |
|
 |
|
6 sides |
Hexagon |
|
 |
|
8 sides |
Octagon |
 |
 |
Definition: Regular Polygon
A shape whose sides have the same length and whose angles have the same measure.
Definition: Irregular Polygon
A shape whose sides differ in length or have angles of different measure.
Hierarchy of Polygons

Polygon Definitions
Definition: Kite
A quadrilateral with two consecutive sides having equal lengths and the other two sides also have equal lengths.
Definition: Trapezoid
A quadrilateral with at least one pair of opposite sides parallel.
Definition: Isosceles Trapezoid
A trapezoid with both angles next to one of the parallel sides having the same size.
Definition: Parallelogram
A trapezoid with pairs of opposite sides parallel.
Definition: Rectangle
A parallelogram with a right angle.
Definition: Rhombus
A quadrilateral with all sides being the same.
Definition: Square
A rectangle that has four equal sides.
Types of Triangles
|
Name |
Definition |
Triangle |
|---|---|---|
|
SIDES |
||
|
Equilateral |
All three sides are equal |
|
|
Isosceles |
Only two sides are equal |
|
|
Scalene |
All three sides are different in length |
 |
|
ANGLES |
||
|
Acute |
Each angle is less than 900 |
 |
|
Right |
One angle is 900 |
 |
|
Obtuse |
One angle is more than 900 |
 |
Partner Activity 1
Draw the following triangles
- Isosceles right triangle
- Scalene obtuse triangle
- Equilateral right triangle
Partner Activity 2
- Is a rectangle a square? Is a square a rectangle?
- Multiple Choice: Which one is NOT a name for the figure below?
- Polygon
- Quadrilateral
- Parallelogram
- Trapezoid

-
What is the difference between a regular and irregular polygon?
Facts about Angles

- Angles in a triangle add up to 1800
- An angle forming a straight line is also 1800
- Any quadrilateral (4-sided figure) is 3600
- Angles which round a point add up to 3600
- The two base angles of an isosceles triangle are equal
Why does a triaangle add up to 180∘
A full circle is 360∘. Half of a circle, called a semicircle, would then be 180∘. The diameter (a line which passes through the center of the circle) of the semicircle is then also 180∘. Therefore, all straight lines are 180∘. See the figure below. Knowing that all straight lines are 180∘, we look at the figure below of the line and triangle.

Since a line is 180∘, we know that angles A1, B, and C1 must add up to 180∘. A theorem (proven statement) in Geometry states that alternate (opposite sides) interior angles are congruent (equal). Angles A1 and A2 are alternate interior, cut by the transversal (line) connecting angle A2 to the straight line. Angles C1 and C2 follow a similar approach.
Since the measures of angles A1=A2, C1=C2, and A1+B+C1=180, then by substitution, A2+B+C2=180. Therefore, triangle A2BC2 adds up to 180∘.
Partner Activity 3
The sum of the interior angles of any polygon is represented by: 180(n−2).
- Find the sum of the interior angles of a triangle, using the formula.
- Find the sum of the interior angles of a pentagon, using the formula.
- Find the sum of the interior angles of a 15-sided polygon, using the formula.
- What is the sum of the EXTERIOR angles of a pentagon?
Complementary and Supplementary Angles
Definition: Complementary Angles
Complementary angles are any two angles with a sum of 900. See angles C and D below.

Definition: Supplementary Angles
Supplementary angles are any two angles with a sum of 1800. See angles A and B below.

Partner Activity 4
- You have two supplementary angles. One angle is 300. What is the measure of the other angle?
- One angle is complementary to another angle. The first one is 490. What is the measure of the second angle?
Practice Problems
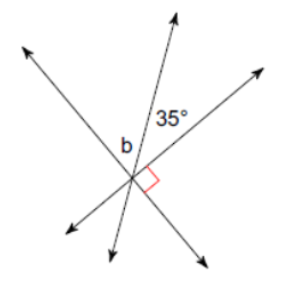
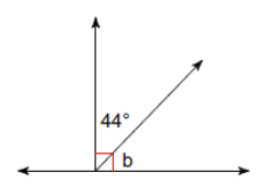
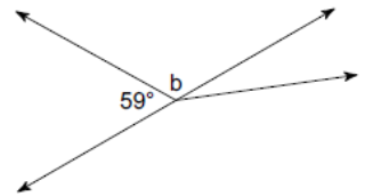
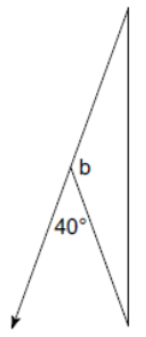
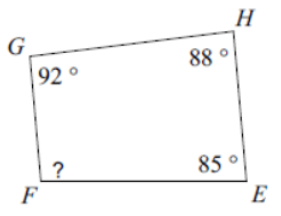
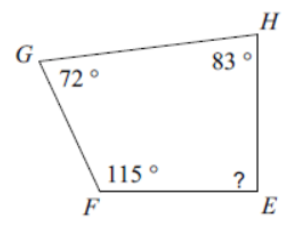
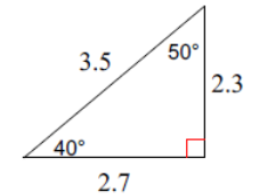
(Problems 1 – 4) Find the measure of angle b.
(Problems 5 – 6) Find the measure of each angle indicated.
(Problems 7 – 10) Classify each angle as acute, obtuse, right or straight.
-
121∘
-
180∘
-
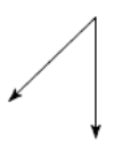
-
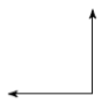
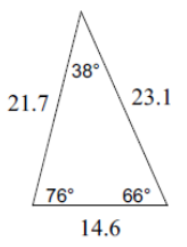
(Problems 11 – 12) Classify each triangle by its angles.
(Problems 13 – 14) Classify each triangle by its angles and sides.
(Problems 15 – 16) Sketch an example of the type of triangle described.
-
Acute Isosceles
-
Right Obtuse
(Problems 17 – 18) Write the name of each polygon.
(Problems 19 – 22) Find the interior angle sum for each polygon. Round your answer to the nearest tenth, if necessary.
(Problems 23 – 26) State if the polygon is regular or irregular.