3.6e: Exercises - Zeroes of Polynomial Functions

Last updated

Feb 26, 2025
Save as PDF
- 3.6: Zeros of Polynomial Functions
- 3.7: The Reciprocal Function

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

A: Concepts

Exercise $\PageIndex{A}$ : Concepts

1) Describe a use for the Remainder Theorem.

2) Explain why the Rational Zero Theorem does not guarantee finding zeros of a polynomial function.

3) What is the difference between rational and real zeros?

4) If Descartes’ Rule of Signs reveals a $0$ or $1$ change of signs, what specific conclusion can be drawn?

5) If synthetic division reveals a zero, why should we try that value again as a possible solution?

Answers to odd exercises:

1. The theorem can be used to evaluate a polynomial.

3. Rational zeros can be expressed as fractions whereas real zeros include irrational numbers.

5. Polynomials can have repeated zeros, so the fact that number is a zero doesn’t preclude it being a zero again.

B: Use the Remainder Theorem to Evaluate a Polynomial

Exercise $\PageIndex{B}$ : Use the Remainder Theorem

$\bigstar$ Use synthetic division to evaluate $p(c)$ and write $p(x)$ in the form $p(x) = (x-c) q(x) +r$ .

6. $p(x) = 2x^2 - x + 1$ , $c = 4$

7. $p(x) = 4x^2-33x-180$ , $c = 12$

8. $p(x) = 2x^3 - x + 6$ , $c=-3$

9. $p(x) = x^3+2x^2+3x+4$ , $c =-1$

10. $p(x) =3x^3-6x^2+4x-8$ , $c=2$

11. $p(x) = 8x^3+12x^2+6x+1$ , $c =-\frac{1}{2}$

12. $p(x) = 2x^4 +x^3- 4x^2+10x-7$ , $c=\frac{3}{2}$

13. $p(x) = x^4 - 3x^3 - 20x^2 - 24x - 8$ , $c =7$

14. $p(x) = x^4 - 5x^2 - 8x -12$ , $c=3$

15. $p(x) = x^4 - 5x^3 + x^2 + 5$ , $c =2$

Answers to odd exercises:

7. $p(12) =0$ , $p(x) = (x-12)(4x+15)$

9. $p(-1)=2$ , $p(x) = (x+1)(x^2 + x+2) + 2$

11. $p\left(-\frac{1}{2}\right) = 0$ , $p(x) = (2x+1)(4x^2+4x+1)$

13. $p(7)=216$ , $p(x) = (x-7)(x^3+4x^2 +8 x+32) + 216$

15. $p(2)=-15$ , $p(x) = (x-2)(x^3-3x^2 -5x -10) -15$

C: Given one zero or factor, find all Real Zeros, and factor a polynomial

Exercise $\PageIndex{C}$ : Use the Factor Theorem given one zero or factor

$\bigstar$ Given a polynomial and one of its factors, find the rest of the real zeros and write the polynomial as a product of linear and irreducible quadratic factors.

17) $f(x)=2x^3+x^2−5x+2;$ Factor: $( x+2)$

18) $f(x)=3x^3+x^2−20x+12;$ Factor: $( x+3)$

19) $f(x)=2x^3+3x^2+x+6;$ Factor: $(x+2)$

20) $f(x)=−5x^3+16x^2−9;$ Factor: $(x−3)$

21) $f(x)=x^3+3x^2+4x+12;$ Factor: $(x+3)$

22) $f(x)=4x^3−7x+3;$ Factor: $(x−1)$

23) $f(x)=2x^3+5x^2−12x−30;$ Factor: $(2x+5)$

24) $f(x)=2x^3−9x^2+13x−6;$ Factor: $(x−1)$

Answers to odd exercises:

17. $−2, 1, \frac{1}{2}$ ; $f(x)=(x+2)(x-1)(2x-1)$

19. $−2$ ; $f(x)=(x+2)(2x^2-x+3)$

21. $−3$ ; $f(x)=(x+3)(x^2+4)$

23. $−\frac{5}{2},\; \sqrt{6},\; −\sqrt{6};$ $f(x)=(2x+5)(x-\sqrt{6})(x+\sqrt{6})$

$\bigstar$ Given a polynomial and $c$ , one of its zeros, find the rest of the real zeros and write the polynomial as a product of linear and irreducible quadratic factors. It is possible some factors are repeated.

25. $p(x)=x^{3} - 24x^{2} + 192x - 512, \;\; c = 8$

26. $p(x)=3x^{3} + 4x^{2} - x - 2, \;\; c = \frac{2}{3}$

27. $p(x)=2x^3-3x^2-11x+6, \;\; c=\frac{1}{2}$

28. $p(x)=x^3+2x^2-3x-6, \;\; c = -2$

29. $p(x)=2x^3-x^2-10x+5, \;\; c=\frac{1}{2}$

30. $p(x)=4x^{4} - 28x^{3} + 61x^{2} - 42x + 9,\; c = \frac{1}{2}$

31. $p(x)=x^5+2x^4-12x^3-38x^2-37x-12,$ $\; c=-1$

32. $p(x)=2x^5 +7x^4 - 18x^2 - 8x +8,$ $\; c = \frac{1}{2}$

33. $p(x)=3x^5 +2x^4 - 15x^3 -10x^2 +12x +8,$ $\; c = -\frac{2}{3}$

Answers to odd exercises:

25. zeros: $8$ ; $p(x)= (x - 8)^{3}$

27. zeros: $\frac{1}{2}, -2, 3$ ; $p(x)= (2x-1)(x+2)(x-3)$

29. zeros: $\frac{1}{2}, \pm \sqrt{5}$ ; $p(x)= (2x-1)(x+\sqrt{5})(x-\sqrt{5})$

31. zeros: $-1,$ $-3,$ $4$ ; $p(x)= (x+1)^3(x+3)(x-4)$

33. zeros: $-2,\; -1,\; -\frac{2}{3},\; 1,\; 2 \\$ ;
$\quad$ $p(x)= (x+2)(x+1)(x-1)(x-2)(3x+2)$

D: List all Possible Rational Zeros

Exercise $\PageIndex{D}$ : Use the Rational Zero Theorem

$\bigstar$ Use the Rational Zeros Theorem to list all possible rational zeros for each given function.

35) $f(x)=2x^3+3x^2−8x+5$

36) $f(x)=3x^3+5x^2−5x+4$

37) $f(x)=6x^4−10x^2+13x+1$

38) $f(x)=4x^5−10x^4+8x^3+x^2−8$

39. $f(x) = x^{3} - 2x^{2} - 5x + 6$

40. $f(x) = x^{4} + 2x^{3} - 12x^{2} - 40x - 32$

41. $f(x) = x^{3} - 7x^{2} + x - 7$

42. $f(x) = x^{3} + 4x^{2} - 11x + 6$

43. $f(x) = x^{4} - 9x^{2} - 4x + 12$

44. $f(x) = -2x^{3} + 19x^{2} - 49x + 20$

45. $f(x) = -17x^{3} + 5x^{2} + 34x - 10$

46. $f(x) = 36x^{4} - 12x^{3} - 11x^{2} + 2x + 1$

47. $f(x) = 3x^{3} + 3x^{2} - 11x - 10$

48. $f(x) = 2x^4+x^3-7x^2-3x+3$

Answers to odd exercises:

35. $±5, ±1, ± \frac{1}{2}, ± \frac{5}{2}$

37. $±1, ±\frac{1}{2}, ±\frac{1}{3}, ±\frac{1}{6}$

39. $\pm 1$ , $\pm 2$ , $\pm 3$ , $\pm 6$ $\qquad \qquad$ 41. $\pm 1$ , $\pm 7$

43. $\pm 1$ , $\pm 2$ , $\pm 3$ , $\pm 4$ , $\pm 6$ , $\pm 12$

45. $\pm 1$ , $\pm 2$ , $\pm 5$ , $\pm 10$ , $\pm \frac{1}{17}$ , $\pm \frac{2}{17}$ , $\pm \frac{5}{17}$ , $\pm \frac{10}{17}$

47. $\pm 1$ , $\pm 2$ , $\pm 5$ , $\pm 10$ , $\pm \frac{1}{3}$ , $\pm \frac{2}{3}$ , $\pm \frac{5}{3}$ , $\pm \frac{10}{3}$

E: Find all Zeros that are Rational

Exercise $\PageIndex{E}$ : Find all zeros that are rational

$\bigstar$ Use the Rational Zero Theorem to find all real number zeros.

49) $x^3−3x^2−10x+24=0$

50) $2x^3+7x^2−10x−24=0$

51) $x^3+2x^2−9x−18=0$

52) $x^3+5x^2−16x−80=0$

53) $x^3−3x^2−25x+75=0$

54) $2x^3−3x^2−32x−15=0$

55) $2x^3+x^2−7x−6=0$

56) $2x^3−3x^2−x+1=0$

57) $3x^3−x^2−11x−6=0$

58) $x^4−2x^3−7x^2+8x+12=0$

59) $4x^3−3x+1=0$

60) $4x^4+4x^3−25x^2−x+6=0$

61) $x^4+2x^3−9x^2−2x+8=0$

62) $x^4+2x^3−4x^2−10x−5=0$

63) $-5x^4+4x^3−19x^2+16x+4=0$

Answers to odd exercises:

49.

$-3,\; 2,\; 4$

51. $-2,\; 3,\; −3$

53.

$3, −5, 5$

55. $2,\; -1,\; -\frac{3}{2}$

57.

$-\frac{2}{3} ,\; \frac{1 \pm \sqrt{13}}{2}$

59. $-1,\; \frac{1}{2}$

61.

$1,\; 2,\; −1,\; −4$

63. $−\frac{1}{5},\; 1$

$\bigstar$ Find the real zeros of the polynomial. State the multiplicity of each real zero.

65. $f(x) = x^{3} - 2x^{2} - 5x + 6$

66. $f(x) = x^{3} + 4x^{2} - 11x + 6$

67. $f(x) = x^{4} - 9x^{2} - 4x + 12$

68. $f(x) = -17x^{3} + 5x^{2} + 34x - 10$

69. $f(x) = 36x^{4} - 12x^{3} - 11x^{2} + 2x + 1$

70. $f(x) = 2x^4+x^3-7x^2-3x+3$

71. $f(x) = 2x^{3} + 7x^{2} +4x - 4$

72. $f(x) = -2x^4 - 3x^3 +10x^2 + 12x - 8$

Answers to odd exercises:

65. $x = 1$ (mult. 1), $x = 3$ (mult. 1), $x = -2$ (mult. 1)

67. $x = -2$ (mult. 2), $x = 1$ (mult. 1), $x = 3$ (mult. 1)

69. $x = \frac{1}{2}$ (mult. 2), $x = -\frac{1}{3}$ (mult. 2)

71. $x = -2$ (mult. 2), $x = \frac{1}{2}$ (mult. 1)

F: Find all zeros (both real and imaginary)

Exercise $\PageIndex{F}$ : Find all zeros

$\bigstar$ Use the Rational Zero Theorem to find all complex solutions (real and non-real).

72.5) $x^3+x^2+x+1=0$

73) $x^3−8x^2+25x−26=0$

74) $x^3+13x^2+57x+85=0$

75) $3x^3−4x^2+11x+10=0$

76) $x^4+2x^3+22x^2+50x−75=0$

77) $2x^3−3x^2+32x+17=0$

Answers to odd exercises:

73.

$2, 3+2i, 3−2i$

75.

$−\dfrac{2}{3}, 1+2i, 1−2i$

77.

$−\dfrac{1}{2}, 1+4i, 1−4i$

G: Find all zeros and sketch

Exercise $\PageIndex{G}$ : Find all zeros and sketch

$\bigstar$ Determine the end behaviour, all the real zeros, their multiplicity, and y-intercept. Sketch the function. (Use synthetic division to find a rational zero. Use the quotient to find the next zero).

78) $f(x)=x^3−1$

79) $f(x)=x^4−x^2−1$

80) $f(x)=x^3−2x^2−5x+6$

81) $f(x)=2x^3+37x^2+200x+300$

82) $f(x)=x^4+2x^3−12x^2+14x−5$

83) $f(x)=2x^4−5x^3−5x^2+5x+3$

84) $f(x)=x^3−2x^2−16x+32$

85) $f(x)=-x^3−7x^2-8x+16$

86. $f(x) = -x^4 - 4x^3+3x^2 +10x -8$

87. $f(x) = x^{4} - 6x^{3} + 8x^{2} + 6x - 9$

88. $f(x) = x^{4} + 4x^{3} - 5x^{2} - 36x - 36$

89. $f(x) = x^{5} - x^{4} - 5x^{3} + x^{2} + 8x + 4$

90. $f(x) = x^{4} + 2x^{3} + 6x - 9$

Answers to odd exercises:

79. zeros (odd multiplicity): $\pm \sqrt{ \frac{1+\sqrt{5} }{2} }$ , 2 imaginary zeros, y-intercept $(0, 1)$

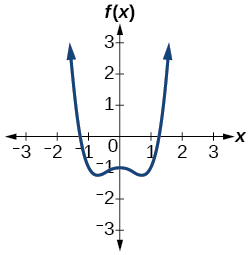
$CNX_PreCalc_Figure_03_06_202.jpg$

81. zeros (odd multiplicity): $\{-10, -6, \frac{-5}{2} \}$ ; y-intercept: $(0, 300)$

$CNX_PreCalc_Figure_03_06_206 (1).jpg$

83. zeros (odd multiplicity); $\{ -1, 1, 3, \frac{-1}{2} \}$ , y-intercept $(0,3)$ .

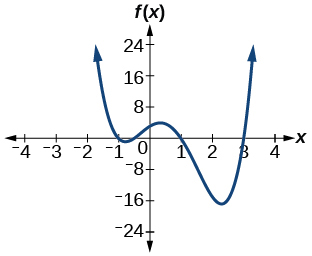
$CNX_PreCalc_Figure_03_06_208.jpg$

85. zeros; $-4$ (multiplicity $2$ ), $1$ (multiplicity $1$ ), y-intercept $(0,16)$ .

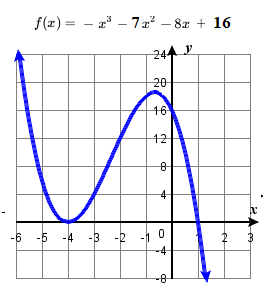
$3.6E #85.png$

87. odd multiplicity zeros: $\{1, -1\}$ ; even multiplicity zero: $\{ 3 \}$ ; y-intercept $(0, -9)$ .

$3.6E #87.png$

89. odd multiplicity zero: $\{ -1 \}$ , even multiplicity zero $\{ 2 \}$ . y-intercept $(0, 4)$ .

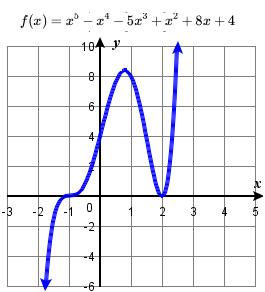
$3.6E #89.png$

H: Given zeros, construct a polynomial function

Exercise $\PageIndex{H}$ : Given zeros, construct a polynomial function

$\bigstar$ Construct a polynomial function of least degree possible using the given information. You may leave the polynomial in factored form.

91) A lowest degree polynomial with real coefficients and zero $3i$

92) A lowest degree polynomial with rational coefficients and zeros: $2$ and $\sqrt{6}$

93) A lowest degree polynomial with integer coefficients and Real roots: $–1$ (with multiplicity $2$ ), and $1$ .

94) A lowest degree polynomial with integer coefficients and Real roots: $–2$ , and $\frac{1}{2}$ (with multiplicity $2$ )

95) A lowest degree polynomial with integer coefficients and Real roots: $−\frac{1}{2}, 0,\frac{1}{2}$

96) A lowest degree polynomial with integer coefficients and Real roots: $–4, –1, 1, 4$

97) A lowest degree polynomial with integer coefficients and Real roots: $–1, 1, 3$

98. A lowest degree polynomial with real coefficients and zeros: $-2$ and $-5i$

99. A lowest degree polynomial with real coefficients and zeros: $4$ and $2i$ .

100. The solutions to $p(x) = 0$ are $x = \pm 3$ and $x=6$ . The leading term of $p(x)$ is $7x^4$ .
$\qquad$ The point $(-3,0)$ is a local minimum on the graph of $y=p(x)$ .

101. The solutions to $p(x) =0$ are $x = \pm 3$ , $x=-2$ , and $x=4$ , The leading term of $p(x)$ is $-x^5$ .
$\qquad$ The point $(-2, 0)$ is a local maximum on the graph of $y=p(x)$ .

102. $p$ is degree 4. as $x \rightarrow \infty$ , $p(x) \rightarrow -\infty$ $p$ has exactly three $x$ -intercepts: $(-6,0)$ , $(1,0)$ and $(117,0)$ .
$\qquad$ The graph of $y=p(x)$ crosses through the $x$ -axis at $(1,0)$ .

103. Find a quadratic polynomial with integer coefficients which has $x = \dfrac{3}{5} \pm \dfrac{\sqrt{29}}{5}$ as its real zeros.

Answers to odd exercises:

91. $f(x)=(x^2+9)$

93. $f(x)=(x+1)^2(x-1)$

95. $f(x)=x(2x+1)(2x-1)$

97. $f(x) = (x+1)(x-1)(x-3)$

99. $p(x)= (x-4)(x-2i)(x+2i)=x^3-4x^2+4x-16$

101. $p(x) = -(x + 2)^{2}(x - 3)(x + 3)(x - 4)$

103. $p(x) = 5x^{2} - 6x - 4$

I: Use Intermediate Value Theorem

Exercise $\PageIndex{I}$ : Intermediate Value Theorem

$\bigstar$ Use the Intermediate Value Theorem to confirm the polynomial $f$ has at least one zero within the given interval.

104) $f(x)=x^3−9x$ , between $x=−4$ and $x=−2$ .

105) $f(x)=x^3−9x$ , between $x=2$ and $x=4$ .

106) $f(x)=x^5−2x$ , between $x=1$ and $x=2$ .

107) $f(x)=−x^4+4$ , between $x=1$ and $x=3$ .

108) $f(x)=−2x^3−x$ , between $x=–1$ and $x=1$ .

109) $f(x)=x^3−100x+2$ , between $x=0.01$ and $x=0.1$

Answers to odd exercises:

105.

$f(2)=–10,\; f(4)=28$ .

$\qquad$ Sign change confirms.

107.

$f(1)=3,\; f(3)=–77.$

$\qquad$ Sign change confirms.

109.

$f(0.01)=1.000001,\; f(0.1)=–7.999$ .

$\qquad$ Sign change confirms.

Search

Text Color

Text Size

Margin Size

Font Type

A: Concepts

B: Use the Remainder Theorem to Evaluate a Polynomial

C: Given one zero or factor, find all Real Zeros, and factor a polynomial

D: List all Possible Rational Zeros

E: Find all Zeros that are Rational

F: Find all zeros (both real and imaginary)

G: Find all zeros and sketch

H: Given zeros, construct a polynomial function

I: Use Intermediate Value Theorem

Support Center

How can we help?