5.2e: Exercises - Right Angle Trigonometry

Last updated
Save as PDF

Page ID: 69486

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

A: Given three sides of a right triangle, find all six trigonometric ratios

Exercise $\PageIndex{A}$

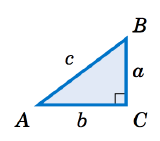
$ \bigstar $ Given right triangle $ABC$ where the right angle is angle $C$ in each figure below,
(a) Label the remaining sides and angles
(b) Designate the hypotenuse, adjacent side or opposite side to angle $A$.
Determine the trigonometric ratios for (c) $\sin A$, (d) $\cos A$, (e) $\tan A$, (f) $\sec A$, (g) $\csc A$, (h) $\cot A$.
Give simplified exact answers - reduce fractions, rationalize all denominators!

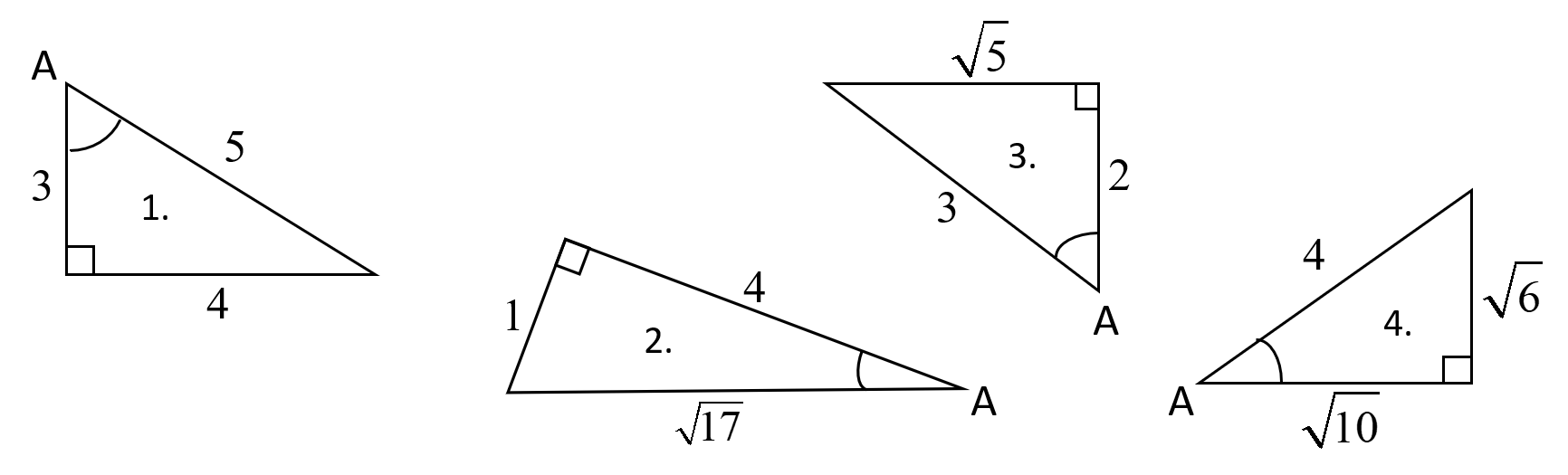
$5.2e #1-#4 triangles.png$

Answers to odd exercises.

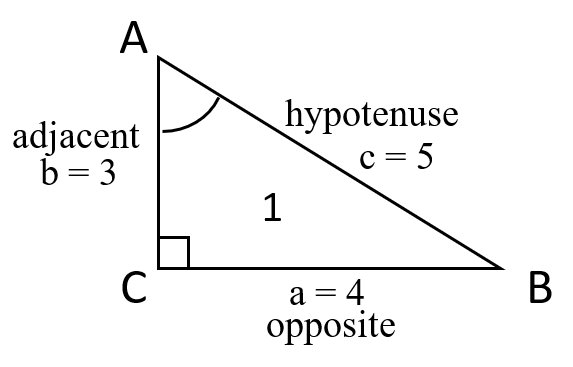$5.2 #1 answer diagram.png$ 1. (c) $\sin A = \frac{4}{5} $, (d) $\cos A = \frac{3}{5} $, (e) $\tan A = \frac{4}{3} $,
(f) $\sec A = \frac{5}{3} $, (g) $\csc A = \frac{5}{4} $, (h) $\cot A = \frac{3}{4} $

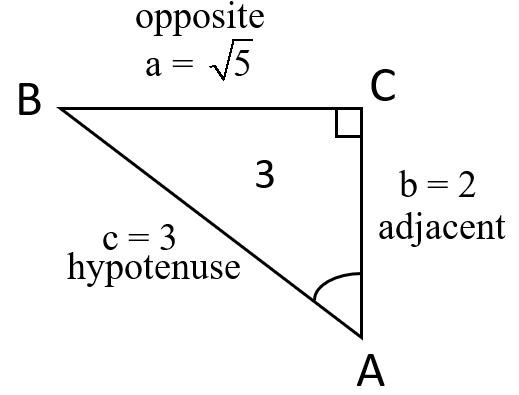$5.2 #3 answer diagram.png$ 3. (c) $\sin A = \frac{\sqrt{5}}{3} $, (d) $\cos A = \frac{2}{3} $, (e) $\tan A = \frac{\sqrt{5}}{2} $,
(f) $\sec A = \frac{3}{2} $, (g) $\csc A = \frac{3\sqrt{5}}{5} $, (h) $\cot A = \frac{2\sqrt{5}}{5} $

B: Given two sides of right triangle, find all trigonometric ratios of the acute angles

Exercise $\PageIndex{B}$

$ \bigstar $ Find the exact values of all six trigonometric functions of angles $A$ and $B $ in the right triangle $\triangle\,ABC $ illustrated below. Simplify!

$alt$

5. $b = 12 $, $c = 13$

6. $b = 15 $, $c = 17$

7. $a = 7 $, $c = 25$

8. $a = 20 $, $c = 29$

9. $a = 9 $, $b = 40 $

10. $a = 1 $, $b = 2 $

11. $a = 1 $, $b = 3$

12. $a = 2 $, $b = 5$

13. $a = 5 $, $c = 6$

14. $a = 2 $, $c = \sqrt{6} $

15. $b = 7 $, $c = 8$

16. $b = 3 $, $c = \sqrt{15} $

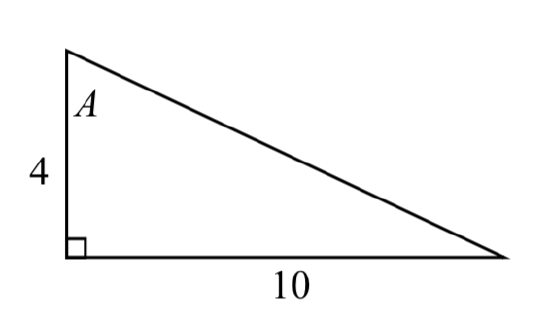
$ \bigstar $ In each of the triangles below, find $\sin \left(A\right), \; \cos \left(A\right),\; \tan \left(A\right),\; \sec \left(A\right),\; \csc \left(A\right),\; \cot \left(A\right)$.

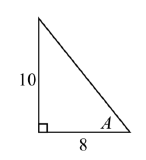17. $屏幕快照 2019-07-08 上午11.11.26.png$ 18. $屏幕快照 2019-07-08 上午11.11.40.png$

Answers to odd exercises.

For all triangles #5-16, the trigonometric ratios can be determined using the following formulas:
$ \sin A = \cos B = \frac{a}{c}, $ $ \cos A = \sin B = \frac{b}{c}, $ $ \tan A = \cot B = \frac{a}{b}, $
$ \csc A = \sec B = \frac{c}{a}, $ $ \sec A = \csc B = \frac{c}{b}, $ $ \cot A = \tan B = \frac{b}{a}, $
The missing side needed to calculate these ratios is given below:
5. $a = 5$ 7. $b = 24$ 9. $c = 41 $ 11. $ c = \sqrt{10} $ 13. $b = \sqrt{11} $ 15. a = $ \sqrt{15} $

17. $\sin \left(A\right) = \frac{5\sqrt{41}}{41}, \; \cos \left(A\right) = \frac{4\sqrt{41}}{41},\; \tan \left(A\right) = \frac{5}{4},\; \sec \left(A\right) = \frac{\sqrt{41}}{4},\; \csc \left(A\right)= \frac{\sqrt{41}}{5},\; \cot \left(A\right) = \frac{4}{5}$

C: Given one trigonometric ratio of an acute angle, find all the others

Exercise $\PageIndex{C}$

$ \bigstar $ Find the exact values of the other five trigonometric functions of the acute angle $A $ given the indicated value of one of the functions. Simplify!

21. $ \sin A= \dfrac{1}{2} $

22. $ \sin A= \dfrac{5}{12} $

23. $\cos A = \dfrac{1}{5}$

24. $\cos A = \dfrac{2}{3}$

25. $\tan A = \dfrac{3}{4}$

26. $\tan A = \dfrac{9}{5}$

27. $\csc A = \dfrac{7}{3}$

28. $\csc A=\dfrac{\sqrt{3}}{1} $

29. $\sec A = 3$

30. $\sec A = \dfrac{5\sqrt{6}}{3}$

31. $ \cot A=10 $

32. $\cot A = 4$

Answers to odd exercises.: 21. $ \sin A = \frac{1}{2}$, $ \cos A = \frac{\sqrt{3}}{2} $, $ \tan A = \frac{\sqrt{3}}{3}$, $\csc A = 2$, $ \sec A = \frac{2\sqrt{3}}{3}$, $ \cot A = \sqrt{3} $
23. $ \sin A = \frac{2\sqrt{6}}{5} $, $ \cos A = \frac{1}{5} $, $ \tan A = 2\sqrt{6} $, $ \csc A = \frac{5\sqrt{6}}{12} $, $ \sec A = 5 $, $ \cot A = \frac{\sqrt{6}}{12} $
25. $ \sin A = \frac{3}{5} $, $ \cos A = \frac{4}{5} $, $ \tan A = \frac{3}{4} $, $ \csc A = \frac{5}{3} $, $ \sec A = \frac{5}{4} $, $ \cot A = \frac{4}{3} $
27. $ \sin A = \frac{3}{7} $, $ \cos A = \frac{2\sqrt{10}}{7} $, $ \tan A = \frac{3\sqrt{10}}{20} $, $ \csc A = \frac{7}{3} $, $ \sec A = \frac{7\sqrt{10}}{20} $, $ \cot A = \frac{2\sqrt{10}}{3} $
29. $ \sin A = \frac{2\sqrt{2}}{3} $, $ \cos A = \frac{1}{3} $, $ \tan A = 2\sqrt{2} $, $ \csc A = \frac{3\sqrt{2}}{4} $, $ \sec A = 3$, $ \cot \theta = \frac{\sqrt{2}}{4} $
31. $ \sin A = \frac{\sqrt{101}}{101} $, $ \cos A = \frac{10\sqrt{101}}{101} $, $ \tan A = \frac{1}{10} $, $ \csc A =\sqrt{101} $, $ \sec A= \frac{\sqrt{101}}{10} $, $ \cot A = 10 $

D: Cofunctions

Exercise $\PageIndex{D}$

Use cofunctions of complementary angles to write an equivalent expression.

36. $ \cos (34°)= \sin (\_\_°)$

37. $ \cos (\dfrac{π}{3})= \sin (\_\_\_) $

38. $ \csc (21°) = \sec (\_\_\_°)$

39. $ \tan (\dfrac{π}{4})= \cot (\_\_)$

Answers to odd exercises.: 37. $\dfrac{π}{6}$ 39. $\dfrac{π}{4}$

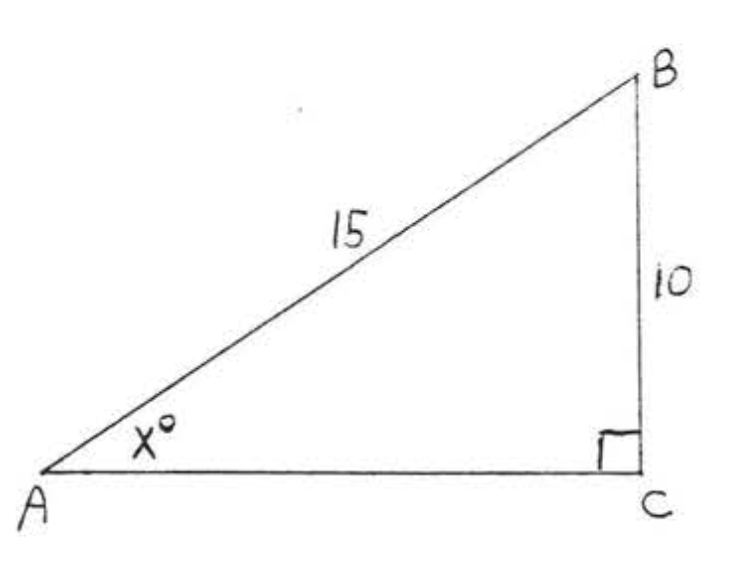
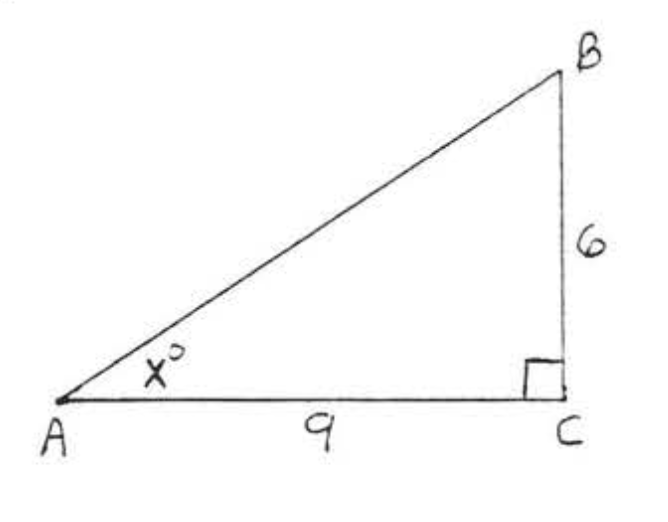
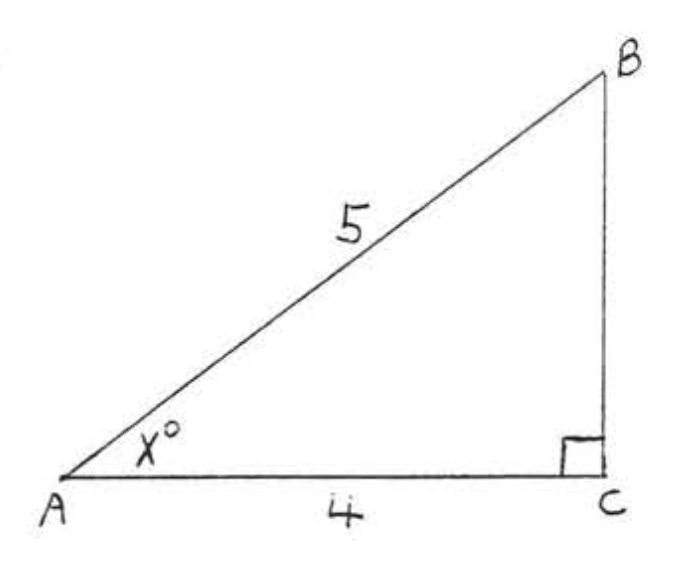
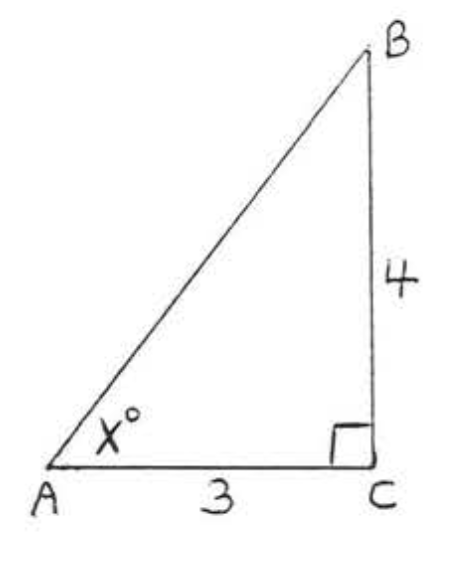
E: Given one side and and an acute angle of a right triangle, find the other sides and angles

Exercise $\PageIndex{E}$

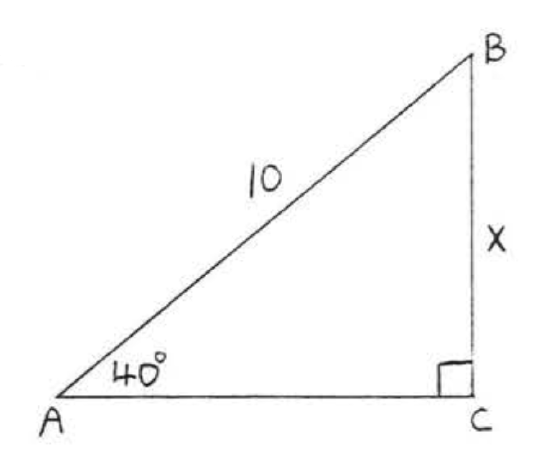
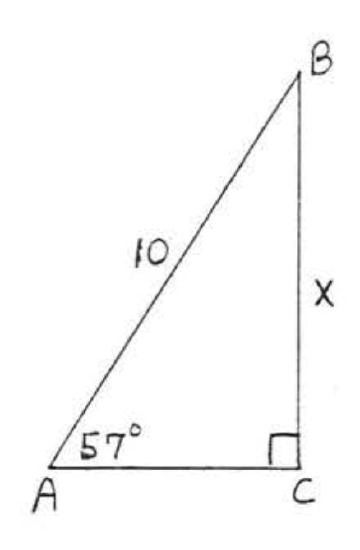
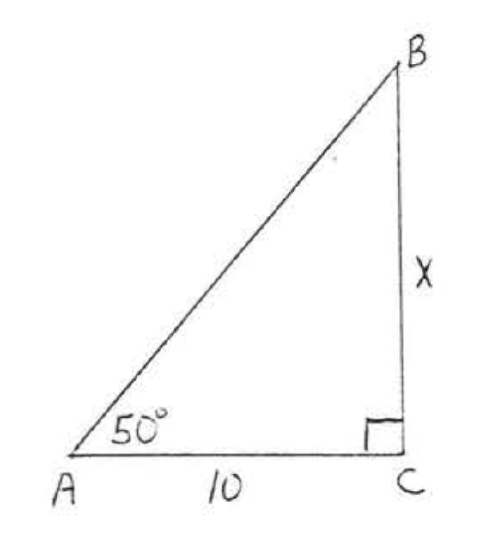
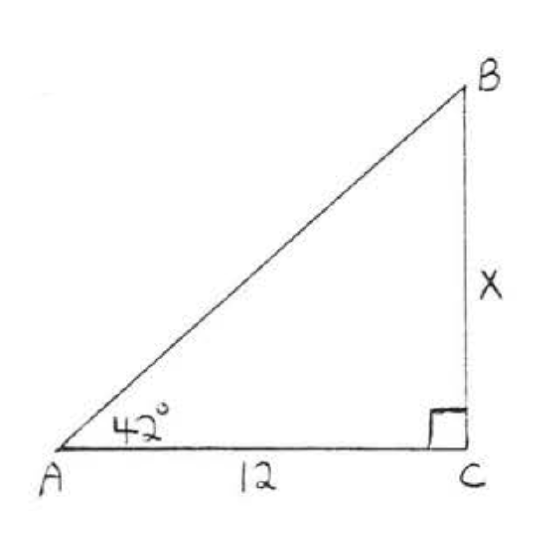
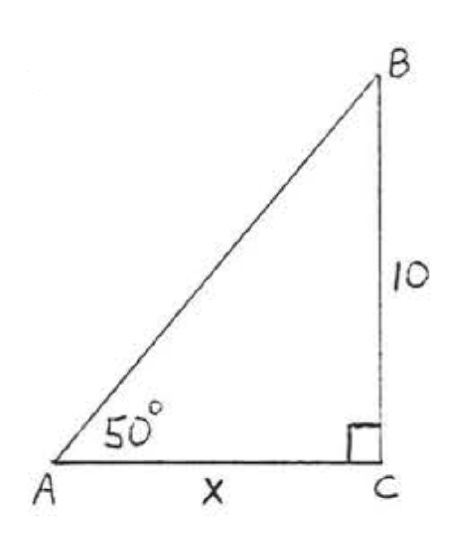
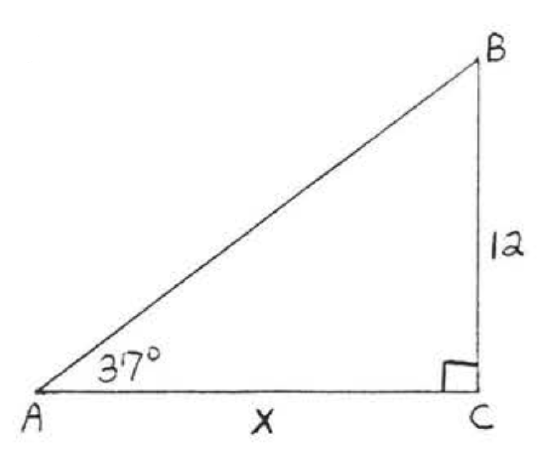
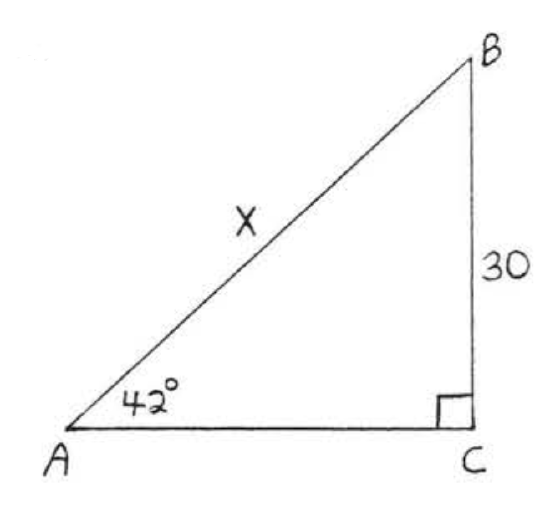
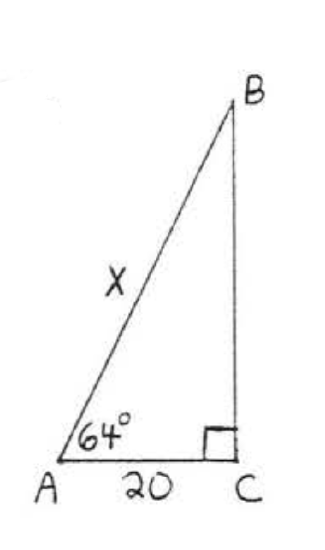
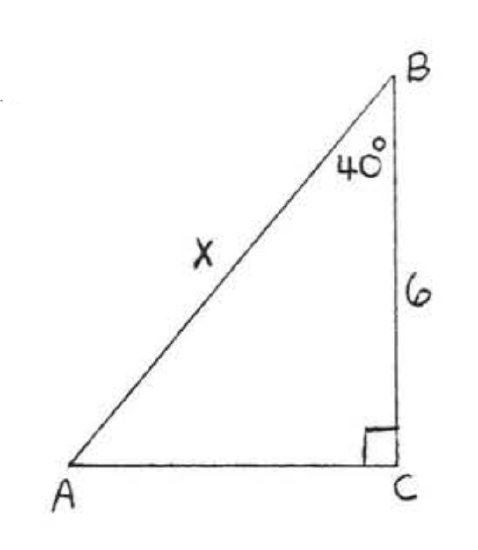
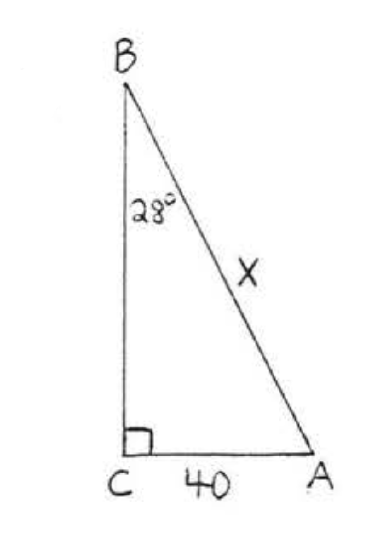
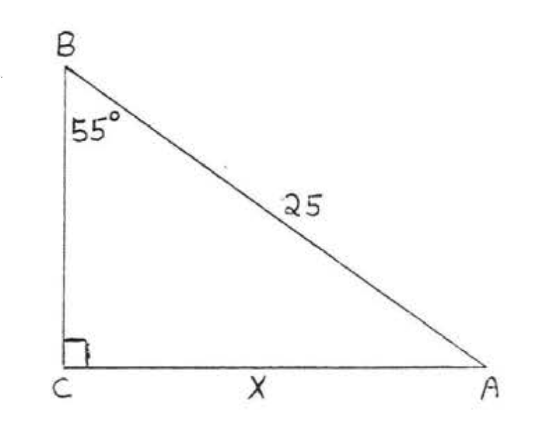
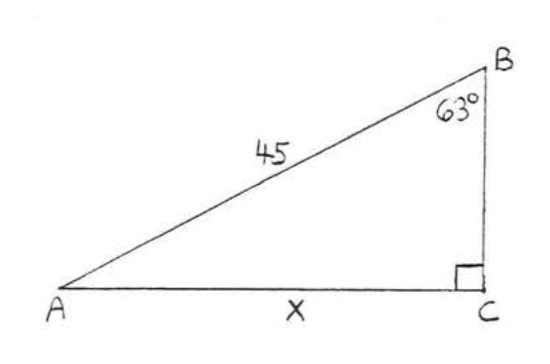
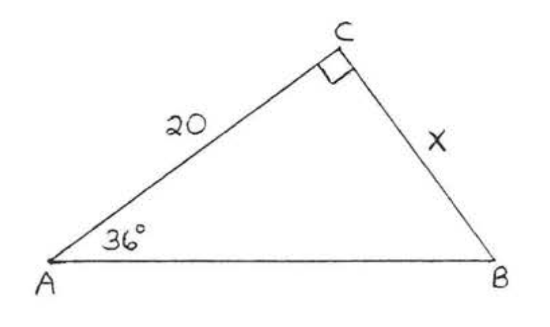
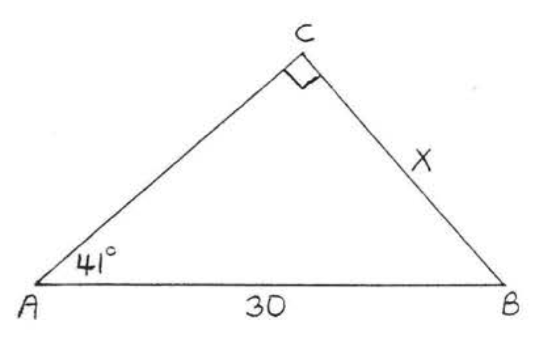
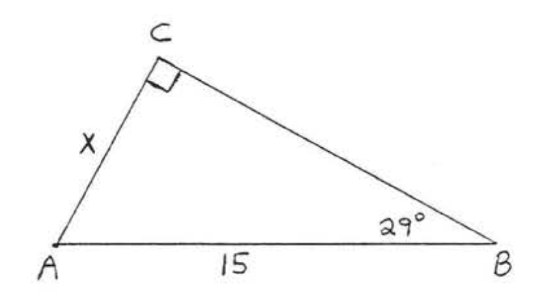
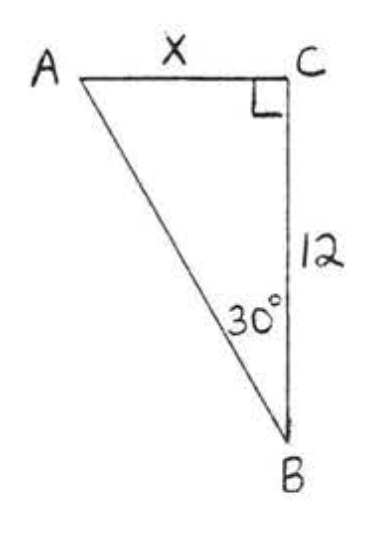
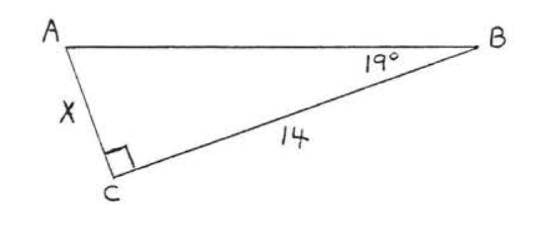
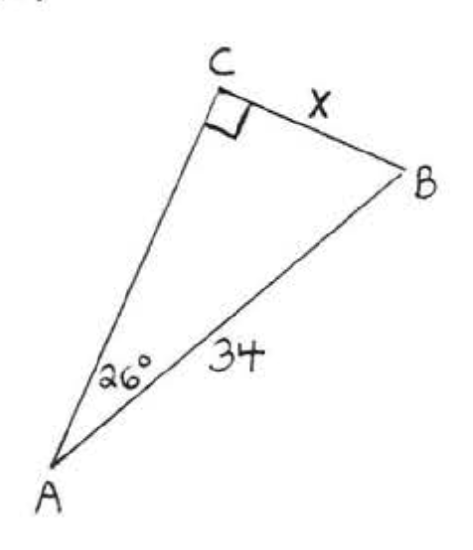
$ \bigstar $ In each of the following triangles, solve for $x$ to the nearest tenth.

41.

$Screen Shot 2020-11-23 at 5.58.20 PM.png$

42.

$Screen Shot 2020-11-23 at 5.58.35 PM.png$

43.

$Screen Shot 2020-11-23 at 5.58.53 PM.png$

44.

$Screen Shot 2020-11-23 at 5.59.26 PM.png$

45.

$Screen Shot 2020-11-23 at 5.59.43 PM.png$

46.

$Screen Shot 2020-11-23 at 5.59.57 PM.png$

47.

$Screen Shot 2020-11-23 at 6.01.48 PM.png$

48.

$Screen Shot 2020-11-23 at 6.02.16 PM.png$

49.

$Screen Shot 2020-11-23 at 6.03.03 PM.png$

50.

$Screen Shot 2020-11-23 at 6.03.27 PM.png$

51.

$Screen Shot 2020-11-23 at 6.03.50 PM.png$

52.

$Screen Shot 2020-11-23 at 6.04.05 PM.png$

Answers to odd exercises.: 41. $6.4$ 43. $7.7$ 45. $11.9$ 47. $8.4$ 49. $44.8$ 51. $7.8$

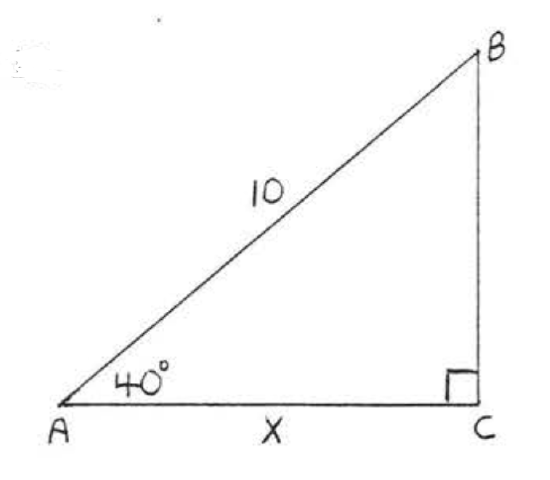
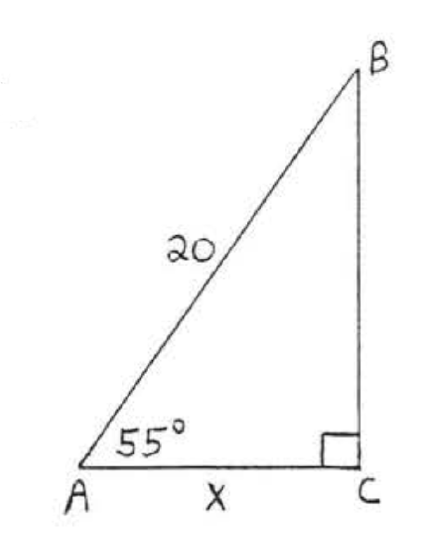
$ \bigstar $ In each of the following triangles, solve for $x$ to the nearest tenth.

53.

$Screen Shot 2020-11-23 at 6.04.23 PM.png$

54.

$Screen Shot 2020-11-23 at 6.04.38 PM.png$

55.

$Screen Shot 2020-11-23 at 6.06.25 PM.png$

56.

$Screen Shot 2020-11-23 at 6.08.16 PM.png$

57.

$Screen Shot 2020-11-23 at 6.09.09 PM.png$

58.

$Screen Shot 2020-11-23 at 6.09.29 PM.png$

59.

$Screen Shot 2020-11-23 at 6.09.50 PM.png$

60,

$Screen Shot 2020-11-23 at 6.10.06 PM.png$

Answers to odd exercises.: 53. $20.5$ 55. $14.5$ 57. $7.3$ 59. $4.8$

$ \bigstar $ In each of the following triangles, solve for the unknown sides and angles. Give answers to 4 decimal digits.

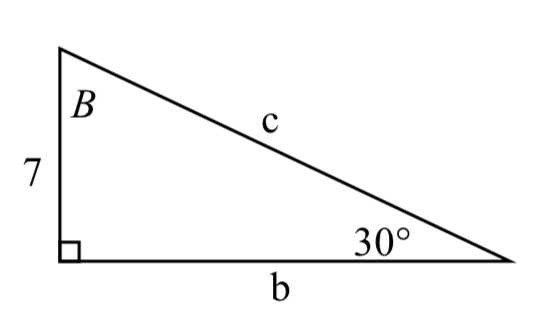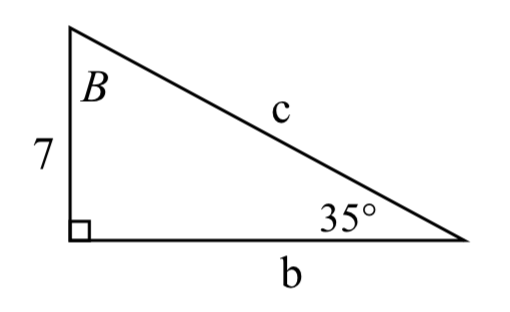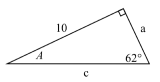
61. $屏幕快照 2019-07-08 上午11.12.00.png$ 62. $屏幕快照 2019-07-08 上午11.12.58.png$ 63. $屏幕快照 2019-07-08 上午11.12.39.png$

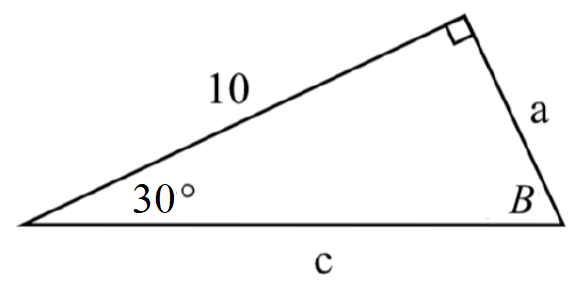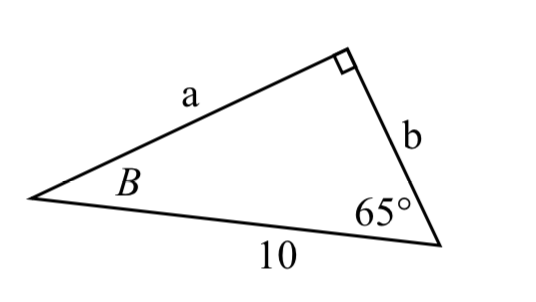64. $5.2 #44.png$ 65. $屏幕快照 2019-07-08 上午11.13.11.png$ 66. $A right triangle with corners labeled A, B, and C. Sides labeled b, c, and 16.5. Angle of 81 degrees also labeled.$

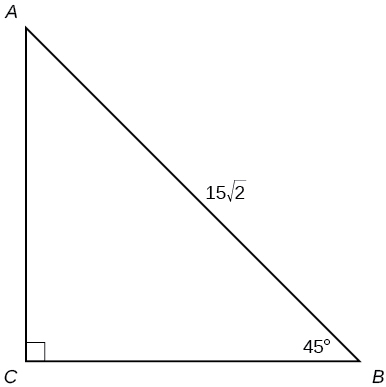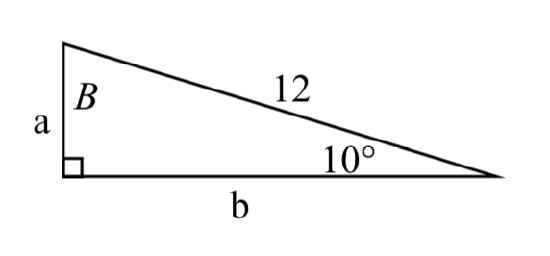
67. $A right triangle with corners labeled A, B, and C. Hypotenuse has length of 15 times square root of 2. Angle B is 45 degrees.$ 68. $屏幕快照 2019-07-08 上午11.13.29.png$

69. $a=5,$ angle opposite side $a$ is $ ∡ A=60^∘$

70. Hypotenuse $c=12,$ and one acute angle is $ ∡ A=45^∘$

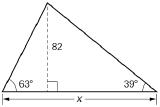
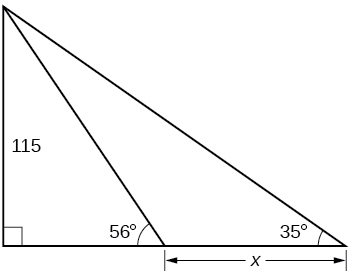
$ \bigstar $ Find $x$. Give answers to 4 decimal digits.

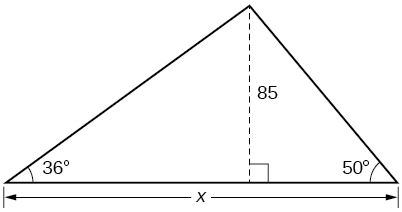71. $A triangle with angles of 36 degrees and 50 degrees and side x. Bisector in triangle with length of 85.$ 72. $A triangle with angles of 63 degrees and 39 degrees and side x. Bisector in triangle with length of 82.$

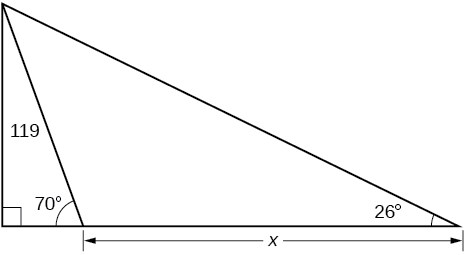73. $A right triangle with side of 119 and angle of 26 degrees. Within right triangle there is another right triangle with angle of 70 degrees instead of 26 degrees. Difference in side length between two triangles is x.$ 74. $A right triangle with side of 115 and angle of 35 degrees. Within right triangle there is another right triangle with angle of 56 degrees. Side length difference between two triangles is x.$

Answers to odd exercises.: 61. $b \approx 12.1244$, $ c =14$, $ B = 60^{\circ} $ 63. $a \approx 5.3171$, $ c \approx 11.3257$, $ A = 28^{\circ} $ 65. $a \approx 9.0631$, $ b \approx 4.2262$, $ B = 25^{\circ} $
67. $a = 15$, $ b = 15$, $ A = 45^{\circ} $ 69. $b \approx 2.8868$, $ c \approx 5.7735$, $ B = 30^{\circ} $ 71. $188.3159$ 73. $200.6737$

F: Right Triangle Applications

Exercise $\PageIndex{F}$

Solve. Round answers to the nearest $10^{th}$ unless otherwise specified.

81. A $23$-ft ladder leans against a building so that the angle between the ground and the ladder is $80°$. How high does the ladder reach up the side of the building?

82. A $33$-ft ladder leans against a building so that the angle between the ground and the ladder is $80°$. How high does the ladder reach up the side of the building?

83. A 20 foot ladder is leaning against a wall, It makes an angle of $70^{\circ}$ with the ground. How high is the top of the ladder from the ground (nearest tenth of a foot)?

84. A 275 foot guy wire is attached to the top of a communication tower. If the wire makes an angle of $53^{\circ}$ with the ground, how tall is the tower?

ANGLE OF ELEVATION

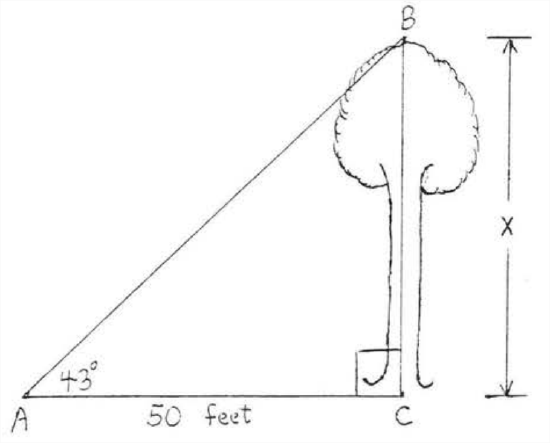
85. At a point 50 feet from a tree the angle of elevation of the top of the tree is $43^{\circ}$. Find the height of the tree to the nearest tenth of a foot.

86. At a point 60 feet from a tree the angle of elevation of the top of the tree is $40^{\circ}$. Find the height of the tree to the nearest tenth of a foot.

87. The angle of elevation to the top of a mountain from a point 20 miles away from the base of the mountain is $6^{\circ}$. How high is the mountain to the nearest foot? One mile is $5280$ feet.

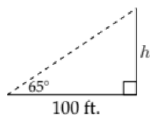
89. At a point 100 feet from a tall building the angle of elevation of the top of the building is $65^{\circ}$. Find the height of the building to the nearest foot.

90. The angle of elevation to the top of a building in New York is found to be $9$ degrees from the ground at a distance of $1$ mile from the base of the building. Using this information, find the height of the building in feet. One mile is $5280$ feet.

91. The angle of elevation to the top of a building in Seattle is found to be $2$ degrees from the ground at a distance of $2$ miles from the base of the building. Using this information, find the height of the building in feet. One mile is $5280$ feet.

93. Assuming that a $370$-foot tall giant redwood grows vertically, if I walk a certain distance from the tree and measure the angle of elevation to the top of the tree to be $60°$, how far from the base of the tree am I?

94. The CN Tower in Toronto is 1815 feet tall. When the angle of elevation to the top of the tower is observed to be $40°$, how far away from the Tower is that location?

ANGLE OF DEPRESSION

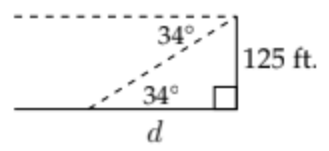
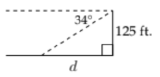
$fig-ch01_patchfile_01.jpg$

95. From the top of a building 125 feet tall, the angle of depression of an intersection is $34^{\circ} .$ How far from the base of the building is the intersection?
Notice that the angle of elevation will be equal to the corresponding angle of depression.

96. A helicopter that is 700 feet in the air measures the angle of depression to a landing pad as $24^{\circ} .$ How far is the landing pad from the point directly beneath the helicopter's current position?

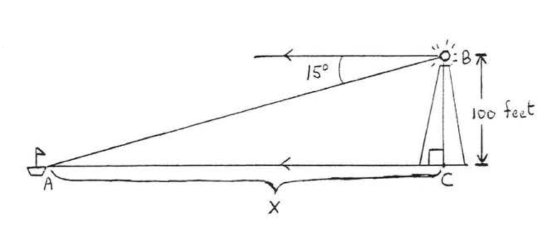
97. From the top of a 100 foot lighthouse the angle of depression of a boat is $15^{\circ}$. How far is the boat from the bottom of the lighthouse (nearest foot)?

98. From the top of a lighthouse 180 feet above sea level, the angle of depression to a ship in the ocean is $28^{\circ} .$ How far is the ship from the base of the lighthouse?

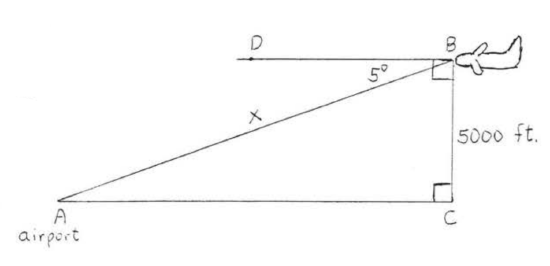
99. From an airplane 5000 feet above the ground the angle of depression of an airport is $5^{\circ}$. How far away is the airport to the nearest hundred feet?

100. From a helicopter 1000 feet above the ground the angle of depression of a heliport is $10^{\circ}$. How far away is the heliport to the nearest foot?

TWO ANGLES of DEPRESSION and/or ELEVATION

101. A radio tower is located $325$ feet from a building. From a window in the building, a person determines that the angle of elevation to the top of the tower is $43°$, and that the angle of depression to the bottom of the tower is $31°$. How tall is the tower?

102. A radio tower is located $400$ feet from a building. From a window in the building, a person determines that the angle of elevation to the top of the tower is $36°$, and that the angle of depression to the bottom of the tower is $23°$. How tall is the tower?

103. A $400$-foot tall monument is located in the distance. From a window in a building, a person determines that the angle of elevation to the top of the monument is $18°$, and that the angle of depression to the bottom of the monument is $3°$. How far is the person from the monument?

104. A $200$-foot tall monument is located in the distance. From a window in a building, a person determines that the angle of elevation to the top of the monument is $15°$, and that the angle of depression to the bottom of the tower is $2°$. How far is the person from the monument?

105. There is lightning rod on the top of a building. From a location $500$ feet from the base of the building, the angle of elevation to the top of the building is measured to be $36°$. From the same location, the angle of elevation to the top of the lightning rod is measured to be $38°$. Assuming the lightning rod is situated at the edge of the building facing the observer, find the height of the lightning rod.

106. There is an antenna on the top of a building. From a location $300$ feet from the base of the building, the angle of elevation to the top of the building is measured to be $40°$. From the same location, the angle of elevation to the top of the antenna is measured to be $43°$. Find the height of the antenna.

Answers to odd exercises.: 81. $22.7$ ft 83. $18.8$ ft 85. $46.6$ feet. 87. $11,099$ feet. 89. $214$ feet. 91. $368.8$ ft 93. $213.6$ ft
95. $d \approx 185.32$ ft 97. $373.2$ ft 99. $57,300$ feet 101. $498.3$ ft 103. $1060.1$ ft 105. $27.4$ ft

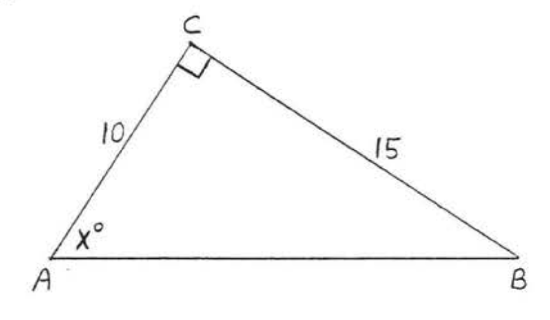
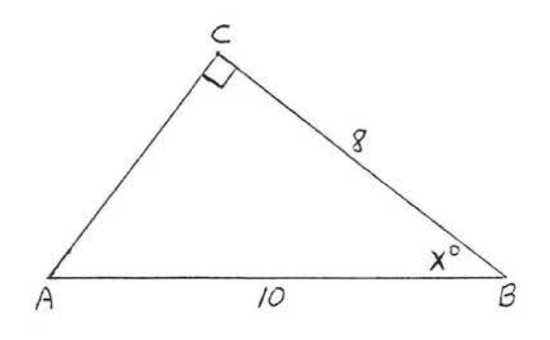
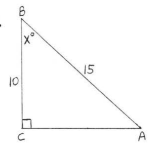
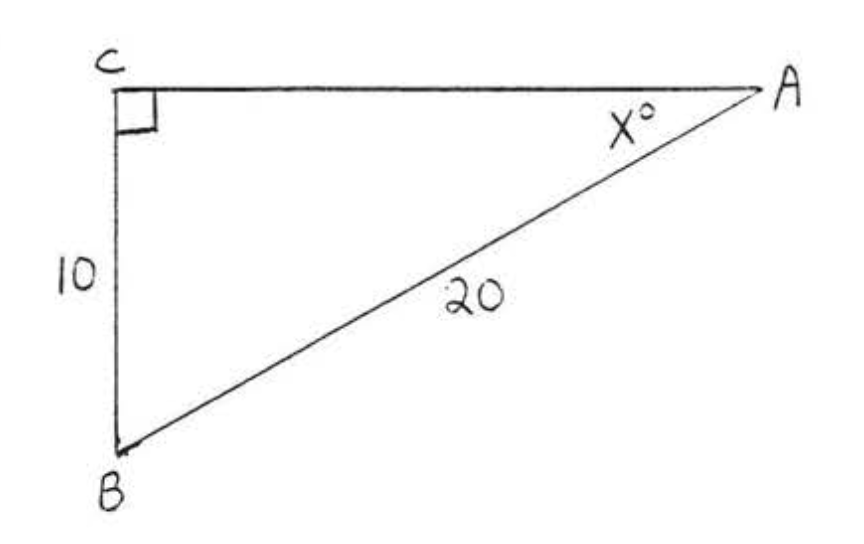
G: Find an angle given 2 sides of a right triangle

Exercise $\PageIndex{G}$

$ \bigstar $ Find the angle $x$ to the nearest tenth of a degree:

111.

$Screen Shot 2020-11-23 at 6.10.45 PM.png$

112.

$Screen Shot 2020-11-23 at 6.11.03 PM.png$

113.

$Screen Shot 2020-11-23 at 6.11.25 PM.png$

114.

$Screen Shot 2020-11-23 at 6.11.43 PM.png$

115.

$Screen Shot 2020-11-23 at 6.12.03 PM.png$

116.

$Screen Shot 2020-11-23 at 6.12.33 PM.png$

117.

$Screen Shot 2020-11-23 at 6.12.48 PM.png$

118.

$Screen Shot 2020-11-23 at 6.13.05 PM.png$

Answers to odd exercises.: 111. $41.8^{\circ}$ 113. $36.9^{\circ}$ 115. $56.3^{\circ}$ 117. $48.2^{\circ}$

H: Applications Finding an Angle

Exercise $\PageIndex{H}$

121. If a 20 foot telephone pole casts a shadow of 43 feet , what is the angle of elevation of the sun to the nearest tenth?

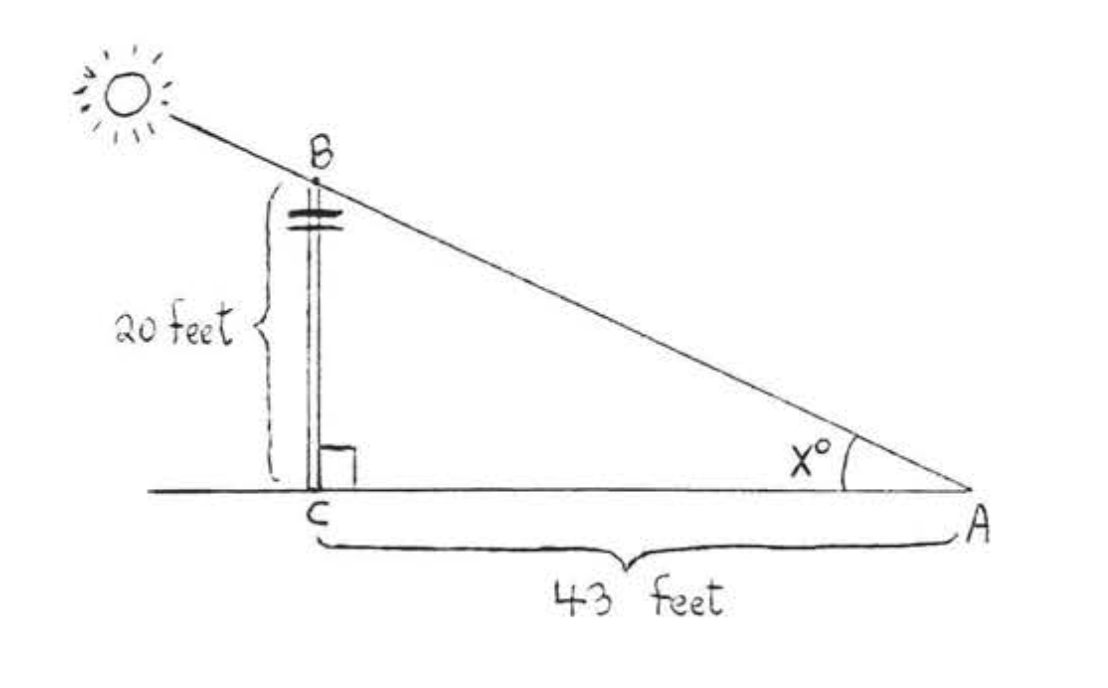
$Screen Shot 2020-11-24 at 1.15.17 PM.png$

122. An 88 foot tree casts a shadow that is 135 feet long. What is the angle of elevation of the sun to the nearest tenth?

123. A road rises 30 feet in a horizontal distance of 300 feet. Find the angle the road makes with the horizontal to the nearest tenth of a degree.

$屏幕快照 2020-11-24 下午1.09.19.png$

124. A road rises 10 feet in a horizontal distance of 400 feet. Find the angle the road makes with the horizontal to the nearest tenth of a degree.

Answers to odd exercises.: 121. $ 24.9^{\circ} $ 123. $5.7^{\circ}$

I: Calculator Practice

Exercise $\PageIndex{I}$

$ \bigstar $ Use a calculator to find the value to four decimal digits. Be sure your calculator is in the appropriate mode!

131. $\sin 10^{\circ}$ 132. $\sin 30^{\circ}$ 133. $\cos 80^{\circ}$ 134. $\cos 60^{\circ}$ 135. $\tan 45^{\circ}$

136. $\tan 60^{\circ}$ 137. $\sin 18^{\circ}$ 138. $\cos 72^{\circ}$ 139. $\tan 50^{\circ}$ 140. $\tan 80^{\circ}$

141. $\sin \left( \dfrac{\pi}{12} \right) $ 142. $\sin \left( \dfrac{5\pi}{12} \right) $ 143. $\cos \left( \dfrac{3\pi}{8} \right) $ 144. $\cos \left( \dfrac{3\pi}{8} \right) $
145. $\tan \left( \dfrac{\pi}{3} \right) $ 146. $\tan \left( 0.8 \right) $ 147. $\sin \left( 1.5 \right) $ 148. $\cos \left( 1.0 \right) $

Answers to odd exercises.: 131. $0.1736$ 133. $0.1736$ 135. $1$ 137. $0.3090$ 139. $1.1918$
141. $0.2588$ 143. $0.3827$ 145. $1.7321$ 147. $0.9975$

$ \bigstar $ Use a calculator to find the value (a) in degrees and (b) in radians to four decimal digits.

151. $\sin^{-1} (.1)$ 152. $\sin^{-1} (.1)$ 153. $\cos^{-1} (.3)$ 154. $\cos^{-1} (.9)$

155. $\tan^{-1} (.5)$ 156. $\tan^{-1} (4)$ 157. $\sin^{-1} (3)$ 158. $\cos^{-1} (2)$

Answers to odd exercises.: 151. (a) $6.7392^{\circ}$ (b) $.1002$ (radians) 153. (a) $72.5425^{\circ}$ (b) $1.2661$ (radians)
155. (a) $26.5651^{\circ}$ (b) $1.3258$ (radians) 157. Undefined ("Domain Error")