6.3E: Exercises for the Shell Method
- Last updated
- Jun 21, 2021
- Save as PDF
- Page ID
- 18204
( \newcommand{\kernel}{\mathrm{null}\,}\)
For exercises 1 - 6, find the volume generated when the region between the two curves is rotated around the given axis. Use both the shell method and the washer method. Use technology to graph the functions and draw a typical slice by hand.
1) [T] Over the curve of y=3x, x=0, and y=3 rotated around the y-axis.
2) [T] Under the curve of y=3x, x=0, and x=3 rotated around the y-axis.
- Answer
-
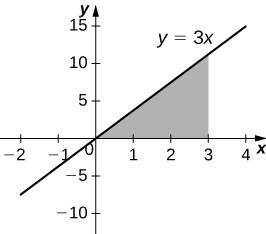
V=54π units3
3) [T] Over the curve of y=3x, x=0, and y=3 rotated around the x-axis.
4) [T] Under the curve of y=3x, x=0, and x=3 rotated around the x-axis.
- Answer
-
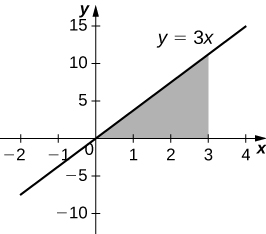
V=81π units3
5) [T] Under the curve of y=2x3,x=0, and x=2 rotated around the y-axis.
6) [T] Under the curve of y=2x3,x=0, and x=2 rotated around the x-axis.
- Answer
-
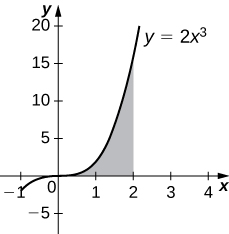
V=512π7 units3
For exercises 7 - 16, use shells to find the volumes of the given solids. Note that the rotated regions lie between the curve and the x-axis and are rotated around the y-axis.
7) y=1−x2, x=0, and x=1
8) y=5x3, x=0, and x=1
- Answer
- V=2π units3
9) y=1x, x=1, and x=100
10) y=√1−x2, x=0, and x=1
- Answer
- V=2π3 units3
11) y=11+x2, x=0,and x=3
12) y=sinx2,x=0, and x=√π
- Answer
- V=2π units3
13) y=1√1−x2, x=0, and x=12
14) y=√x, x=0, and x=1
- Answer
- V=4π5 units3
15) y=(1+x2)3, x=0, and x=1
16) y=5x3−2x4, x=0, and x=2
- Answer
- V=64π3 units3
For exercises 17 - 26, use shells to find the volume generated by rotating the regions between the given curve and y=0 around the x-axis.
17) y=√1−x2, x=0, and x=1
18) y=x2, x=0, and x=2
- Answer
- V=32π5 units3
19) y=ex, x=0, and x=1
20) y=ln(x), x=1, and x=e
- Answer
- V=π(e−2) units3
21) x=11+y2, y=1, and y=4
22) x=1+y2y, y=0, and y=2
- Answer
- V=28π3 units3
23) x=cosy, y=0, and y=π
24) x=y3−4y2, x=−1, and x=2
- Answer
- V=84π5 units3
25) x=yey, x=−1, and x=2
26) x=eycosy, x=0, and x=π
- Answer
- V=eππ2 units3
For exercises 27 - 36, find the volume generated when the region between the curves is rotated around the given axis.
27) y=3−x, y=0, x=0, and x=2 rotated around the y-axis.
28) y=x3, y=0, x=0, and y=8 rotated around the y-axis.
- Answer
- V=64π5 units3
29) y=x2, y=x, rotated around the y-axis.
30) y=√x, x=0, and x=1 rotated around the line x=2.
- Answer
- V=28π15 units3
31) y=14−x, x=1, and x=2 rotated around the line x=4.
32) y=√x and y=x2 rotated around the y-axis.
- Answer
- V=3π10 units3
33) y=√x and y=x2 rotated around the line x=2.
34) x=y3, y=1x, x=1, and y=2 rotated around the x-axis.
- Answer
- 52π5 units3
35) x=y2 and y=x rotated around the line y=2.
36) [T] Left of x=sin(πy), right of y=x, around the y-axis.
- Answer
- V≈0.9876 units3
For exercises 37 - 44, use technology to graph the region. Determine which method you think would be easiest to use to calculate the volume generated when the function is rotated around the specified axis. Then, use your chosen method to find the volume.
37) [T] y=x2 and y=4x rotated around the y-axis.
38) [T] y=cos(πx),y=sin(πx),x=14, and x=54 rotated around the y-axis.
- Answer
-
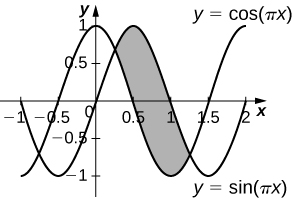
V=3√2 units3
39) [T] y=x2−2x,x=2, and x=4 rotated around the y-axis.
40) [T] y=x2−2x,x=2, and x=4 rotated around the x-axis.
- Answer
-
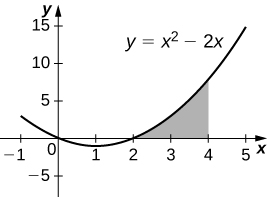
V=496π15 units3
41) [T] y=3x3−2,y=x, and x=2 rotated around the x-axis.
42) [T] y=3x3−2,y=x, and x=2 rotated around the y-axis.
- Answer
-
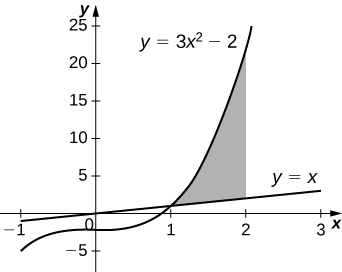
V=398π15 units3
43) [T] x=sin(πy2) and x=√2y rotated around the x-axis.
44) [T] x=y2,x=y2−2y+1, and x=2 rotated around the y-axis.
- Answer
-
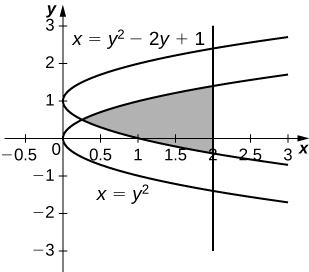
V=15.9074 units3
For exercises 45 - 51, use the method of shells to approximate the volumes of some common objects, which are pictured in accompanying figures.
45) Use the method of shells to find the volume of a sphere of radius r.
46) Use the method of shells to find the volume of a cone with radius r and height h.
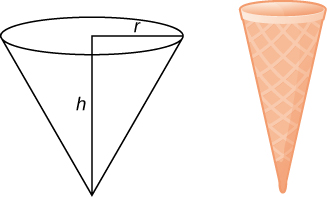
- Answer
- V=13πr2h units3
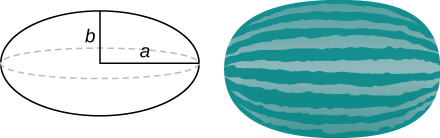
47) Use the method of shells to find the volume of an ellipse (x2/a2)+(y2/b2)=1 rotated around the x-axis.
48) Use the method of shells to find the volume of a cylinder with radius r and height h.
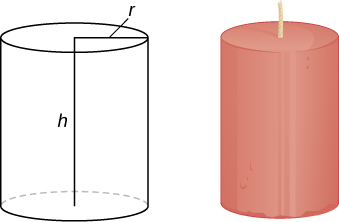
- Answer
- V=πr2h units3
49) Use the method of shells to find the volume of the donut created when the circle x2+y2=4 is rotated around the line x=4.
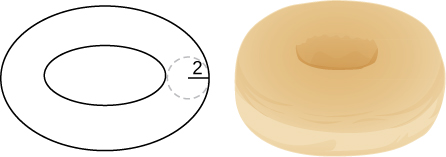
50) Consider the region enclosed by the graphs of y=f(x),y=1+f(x),x=0,y=0, and x=a>0. What is the volume of the solid generated when this region is rotated around the y-axis? Assume that the function is defined over the interval [0,a].
- Answer
- V=πa2 units3
51) Consider the function y=f(x), which decreases from f(0)=b to f(1)=0. Set up the integrals for determining the volume, using both the shell method and the disk method, of the solid generated when this region, with x=0 and y=0, is rotated around the y-axis. Prove that both methods approximate the same volume. Which method is easier to apply? (Hint: Since f(x) is one-to-one, there exists an inverse f−1(y).)
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.


