8.2: Complex Numbers
( \newcommand{\kernel}{\mathrm{null}\,}\)
Complex numbers were first introduced in order to solve some simple problems. The history of complex numbers only extends about five hundred years. In essence, it was found that we need to find the roots of equations such as x2+1=0. The solution is x=±√−1. Due to the usefulness of this concept, which was not realized at first, a special symbol was introduced - the imaginary unit, i=√−1. In particular, Girolamo Cardano (1501−1576) was one of the first to use square roots of negative numbers when providing solutions of cubic equations. However, complex numbers did not become an important part of mathematics or science until the late seventh and eighteenth centuries after people like Abraham de Moivre ( 1667−1754 ), the Bernoulli1 family and Euler took them seriously.
A complex number is a number of the form z=x+iy, where x and y are real numbers. x is called the real part of z and y is the imaginary part of z. Examples of such numbers are 3+3i,−1i=−i,4i and 5. Note that 5=5+0i and 4i=0+4i.
The Bernoullis were a family of Swiss mathematicians spanning three generations. It all started with Jacob Bernoulli (1654−1705) and his brother Johann Bernoulli (1667−1748). Jacob had a son, Nicolaus Bernoulli (1687−1759) and Johann (1667−1748) had three sons, Nicolaus Bernoulli II (1695−1726), Daniel Bernoulli (1700−1872), and Johann Bernoulli II (1710−1790). The last generation consisted of Johann II’s sons, Johann Bernoulli III (1747−1807) and Jacob Bernoulli II (1759−1789). Johann, Jacob and Daniel Bernoulli were the most famous of the Bernoulli’s. Jacob studied with Leibniz, Johann studied under his older brother and later taught Leonhard Euler and Daniel Bernoulli, who is known for his work in hydrodynamics.
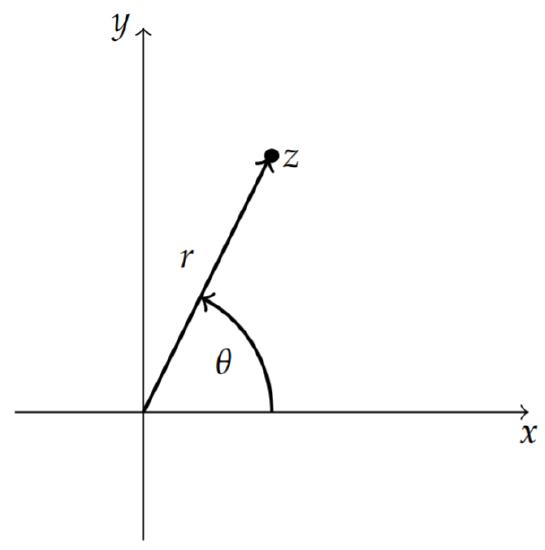
There is a geometric representation of complex numbers in a two dimensional plane, known as the complex plane C. This is given by the Argand diagram as shown in Figure 8.2.1. Here we can think of the complex number z=x+iy as a point (x,y) in the z-complex plane or as a vector. The magnitude, or length, of this vector is called the complex modulus of z, denoted by |z|=√x2+y2. We can also use the geometric picture to develop a polar representation of complex numbers. From Figure 8.2.1 we can see that in terms of r and θ we have that
x=rcosθy=rsinθ
Thus,
z=x+iy=r(cosθ+isinθ)=reiθ.
The complex modulus, |z|=√x2+y2.
Complex numbers can be represented in rectangular (Cartesian), z=x+iy, or polar form, z=reiθ. Here we define the argument, θ, and modulus, |z|=r of complex numbers.
So, given r and θ we have z=reiθ. However, given the Cartesian form, z=x+iy, we can also determine the polar form, since
r=√x2+y2,tanθ=yx.
Note that r=|z|.
Locating 1+i in the complex plane, it is possible to immediately determine the polar form from the angle and length of the "complex vector." This is shown in Figure 8.2.2. It is obvious that θ=π4 and r=√2.
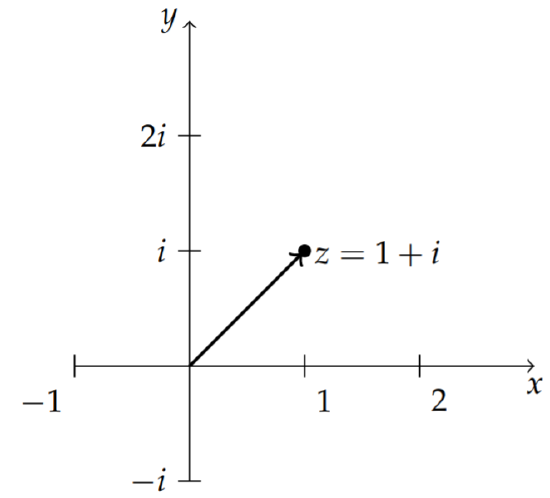
Write z=1+i in polar form.
Solution
If one did not see the polar form from the plot in the z-plane, then one could systematically determine the results. First, write z=1+i in polar form, z=reiθ, for some r and θ.
Using the above relations between polar and Cartesian representations, we have r=√x2+y2=√2 and tanθ=yx=1. This gives θ=π4. So, we have found that
1+i=√2eiπ/4.
We can also define binary operations of addition, subtraction, multiplication and division of complex numbers to produce a new complex number. The addition of two complex numbers is simply done by adding the real and imaginary parts of each number. So,
(3+2i)+(1−i)=4+i.
Subtraction is just as easy,
(3+2i)−(1−i)=2+3i.
We can multiply two complex numbers just like we multiply any binomials, though we now can use the fact that i2=−1. For example, we have
(3+2i)(1−i)=3+2i−3i+2i(−i)=5−i.
We can easily add, subtract, multiply and divide complex numbers.
We can even divide one complex number into another one and get a complex number as the quotient. Before we do this, we need to introduce the complex conjugate, ˉz, of a complex number. The complex conjugate of z=x+iy, where x and y are real numbers, is given as
ˉz=x−iy.
The complex conjugate of z=x+iy, is given as ˉz=x−iy.
Complex conjugates satisfy the following relations for complex numbers z and w and real number x.
¯z+w=ˉz+ˉw¯zw=¯zw¯ˉz=zˉx=x.
One consequence is that the complex conjugate of reiθ is
¯reiθ=¯cosθ+isinθ=cosθ−isinθ=re−iθ.
Another consequence is that
zˉz=reiθre−iθ=r2.
Thus, the product of a complex number with its complex conjugate is a real number. We can also prove this result using the Cartesian form
zˉz=(x+iy)(x−iy)=x2+y2=|z|2.
Now we are in a position to write the quotient of two complex numbers in the standard form of a real plus an imaginary number.
Simplify the expression z=3+2i1−i.
Solution
This simplification is accomplished by multiplying the numerator and denominator of this expression by the complex conjugate of the denominator:
z=3+2i1−i=3+2i1−i1+i1+i=1+5i2.
Therefore, the quotient is a complex number and in standard form it is given by z=12+52i.
We can also consider powers of complex numbers. For example,
(1+i)2=2i(1+i)3=(1+i)(2i)=2i−2.
But, what is (1+i)1/2=√1+i ?
In general, we want to find the nth root of a complex number. Let t= z1/n. To find t in this case is the same as asking for the solution of
z=tn
given z. But, this is the root of an nth degree equation, for which we expect n roots. If we write z in polar form, z=reiθ, then we would naively compute
z1/n=(reiθ)1/n=r1/neiθ/n=r1/n[cosθn+isinθn].
For example,
(1+i)1/2=(√2eiπ/4)1/2=21/4eiπ/8.
But this is only one solution. We expected two solutions for n=2.
The function f(z)=z1/n is multivalued.
z1/n=r1/nei(θ+2kπ)/n,k=0,1,…,n−1
The reason we only found one solution is that the polar representation for z is not unique. We note that
e2kπi=1,k=0,±1,±2,….
So, we can rewrite z as z=reiθe2kπi=rei(θ+2kπ). Now, we have that
z1/n=r1/nei(θ+2kπ)/n,k=0,1,…,n−1
Note that these are the only distinct values for the roots. We can see this by considering the case k=n. Then, we find that
ei(θ+2πin)/n=eiθ/ne2πi=eiθ/n.
So, we have recovered the n=0 value. Similar results can be shown for the other k values larger than n.
Now, we can finish the example we had started.
Determine the square roots of 1+i, or √1+i.
Solution
As we have seen, we first write 1+i in polar form, 1+i=√2eiπ/4. Then, introduce e2kπi=1 and find the roots:
(1+i)1/2=(√2eiπ/4e2kπi)1/2,k=0,1,=21/4ei(π/8+kπ),k=0,1,=21/4eiπ/8,21/4e9πi/8.
The nth roots of unity, n√1.
Finally, what is n√1 ? Our first guess would be n√1=1. But, we now know that there should be n roots. These roots are called the nth roots of unity. Using the above result with r=1 and θ=0, we have that
n√1=[cos2πkn+isin2πkn],k=0,…,n−1.
For example, we have
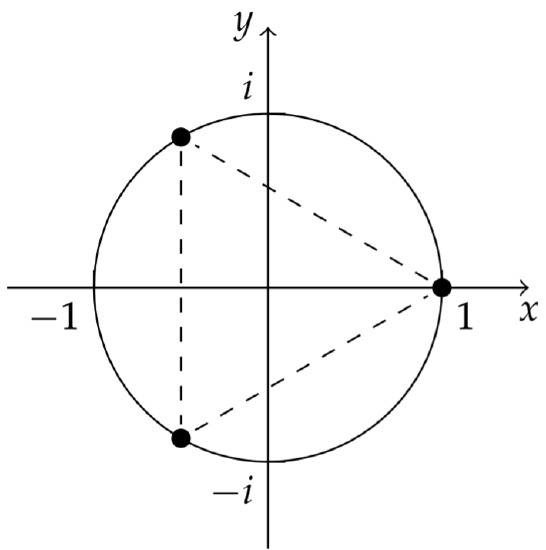
3√1=[cos2πk3+isin2πk3],k=0,1,2
These three roots can be written out as
3√1=1,−12+√32i,−12−√32i.
We can locate these cube roots of unity in the complex plane. In Figure 8.2.3 we see that these points lie on the unit circle and are at the vertices of an equilateral triangle. In fact, all nth roots of unity lie on the unit circle and are the vertices of a regular n-gon with one vertex at z=1.