8.7: Problems
- Page ID
- 90970
Write the following in standard form.
- \((4+5 i)(2-3 i).\)
- \((1+i)^{3}\).
- \(\frac{5+3 i}{1-i}\).
Write the following in polar form, \(z=r e^{i \theta}\).
- \(i-1\).
- \(-2 i\).
- \(\sqrt{3}+3 i\).
Write the following in rectangular form, \(z=a+i b\).
- \(4 e^{i \pi / 6}\).
- \(\sqrt{2} e^{5 i \pi / 4}\).
- \((1-i)^{100}\).
Find all \(z\) such that \(z^{4}=16 i\). Write the solutions in rectangular form, \(z=a+i b\), with no decimal approximation or trig functions.
Show that \(\sin (x+i y)=\sin x \cosh y+i \cos x \sinh y\) using trigonometric identities and the exponential forms of these functions.
Find all \(z\) such that \(\cos z=2\), or explain why there are none. You will need to consider \(\cos (x+i y)\) and equate real and imaginary parts of the resulting expression similar to problem 5.
Find the principal value of \(i^{i}\). Rewrite the base, \(i\), as an exponential first.
Consider the circle \(|z-1|=1\).
- Rewrite the equation in rectangular coordinates by setting \(z=\) \(x+i y\).
- Sketch the resulting circle using part a.
- Consider the image of the circle under the mapping \(f(z)=z^{2}\), given by \(\left|z^{2}-1\right|=1\).
- By inserting \(z=r e^{i \theta}=r(\cos \theta+i \sin \theta)\), find the equation of the image curve in polar coordinates.
- Sketch the image curve. You may need to refer to your Calculus II text for polar plots. [Maple might help.]
Find the real and imaginary parts of the functions:
- \(f(z)=z^{3}\).
- \(f(z)=\sinh (z)\).
- \(f(z)=\cos \bar{z}\).
Find the derivative of each function in Problem 9 when the derivative exists. Otherwise, show that the derivative does not exist.
Let \(f(z)=u+i v\) be differentiable. Consider the vector field given by \(\mathbf{F}=v \mathbf{i}+u \mathbf{j} .\) Show that the equations \(\nabla \cdot \mathbf{F}=\mathbf{0}\) and \(\nabla \times \mathbf{F}=\mathbf{0}\) are equivalent to the Cauchy-Riemann equations. [You will need to recall from multivariable calculus the del operator, \(\nabla=\mathbf{i} \frac{\partial}{\partial x}+\mathbf{j} \frac{\partial}{\partial y}+\mathbf{k} \frac{\partial}{\partial z}\).]
What parametric curve is described by the function \[\gamma(t)=(t-3)+i(2 t+1),\nonumber \] \(0 \leq t \leq 2\) ? [Hint: What would you do if you were instead considering the parametric equations \(x=t-3\) and \(y=2 t+1\) ?]
Write the equation that describes the circle of radius 3 which is centered at \(z=2-i\) in a) Cartesian form (in terms of \(x\) and \(y\) ); b) polar form (in terms of \(\theta\) and \(r\) ); c) complex form (in terms of \(z, r\), and \(e^{i \theta}\) ).
Consider the function \(u(x, y)=x^{3}-3 x y^{2}\).
- Show that \(u(x, y)\) is harmonic; i.e., \(\nabla^{2} u=0\).
- Find its harmonic conjugate, \(v(x, y)\).
- Find a differentiable function, \(f(z)\), for which \(u(x, y)\) is the real part.
- Determine \(f^{\prime}(z)\) for the function in part c. [Use \(f^{\prime}(z)=\frac{\partial u}{\partial x}+i \frac{\partial v}{\partial x}\) and rewrite your answer as a function of \(z\).]
Evaluate the following integrals:
- \(\int_{C} \bar{z} d z\), where \(C\) is the parabola \(y=x^{2}\) from \(z=0\) to \(z=1+i\).
- \(\int_{C} f(z) d z\), where \(f(z)=2 z-\bar{z}\) and \(C\) is the path from \(z=0\) to \(z=2+i\) consisting of two line segments from \(z=0\) to \(z=2\) and then \(z=2\) to \(z=2+i\).
- \(\int_{C} \frac{1}{z^{2}+4} d z\) for \(C\) the positively oriented circle, \(|z|=2\). [Hint: Parametrize the circle as \(z=2 e^{i \theta}\), multiply numerator and denominator by \(e^{-i \theta}\), and put in trigonometric form.]
Let \(C\) be the positively oriented ellipse \(3 x^{2}+y^{2}=9\). Define \[F\left(z_{0}\right)=\int_{C} \frac{z^{2}+2 z}{z-z_{0}} d z .\nonumber \] Find \(F(2 i)\) and \(F(2)\). [Hint: Sketch the ellipse in the complex plane. Use the Cauchy Integral Theorem with an appropriate \(f(z)\), or Cauchy’s Theorem if \(z_{0}\) is outside the contour.]
Show that \[\int_{C} \frac{d z}{(z-1-i)^{n+1}}=\left\{\begin{array}{cc} 0, & n \neq 0 \\ 2 \pi i, & n=0 \end{array}\right. \nonumber \] for \(C\) the boundary of the square \(0 \leq x \leq 2,0 \leq y \leq 2\) taken counterclockwise. [Hint: Use the fact that contours can be deformed into simpler shapes (like a circle) as long as the integrand is analytic in the region between them. After picking a simpler contour, integrate using parametrization.]
Show that for \(g\) and \(h\) analytic functions at \(z_{0}\), with \(g\left(z_{0}\right) \neq 0, h\left(z_{0}\right)=0\), and \(h^{\prime}\left(z_{0}\right) \neq 0\), \[\operatorname{Res}\left[\frac{g(z)}{h(z)} ; z_{0}\right]=\frac{g\left(z_{0}\right)}{h^{\prime}\left(z_{0}\right)} .\nonumber \]
For the following determine if the given point is a removable singularity, an essential singularity, or a pole (indicate its order).
- \(\frac{1-\cos z}{z^{2}}, \quad z=0\).
- \(\frac{\sin z}{z^{2}}, \quad z=0\).
- \(\frac{z^{2}-1}{(z-1)^{2}}, \quad z=1\).
- \(z e^{1 / z}, \quad z=0\).
- \(\cos \frac{\pi}{z-\pi}, \quad z=\pi\).
Find the Laurent series expansion for \(f(z)=\frac{\sinh z}{z^{3}}\) about \(z=0\). [Hint: You need to first do a MacLaurin series expansion for the hyperbolic sine.]
Find series representations for all indicated regions.
- \(f(z)=\frac{z}{z-1},|z|<1,|z|>1\).
- \(f(z)=\frac{1}{(z-i)(z+2)},|z|<1,1<|z|<2,|z|>2\). [Hint: Use partial fractions to write this as a sum of two functions first.]
Find the residues at the given points:
- \(\frac{2 z^{2}+3 z}{z-1}\) at \(z=1\).
- \(\frac{\ln (1+2 z)}{z}\) at \(z=0\).
- \(\frac{\cos z}{(2 z-\pi)^{3}}\) at \(z=\frac{\pi}{2}\).
Consider the integral \(\int_{0}^{2 \pi} \frac{d \theta}{5-4 \cos \theta}\).
- Evaluate this integral by making the substitution \(2 \cos \theta=z+\frac{1}{z}\), \(z=e^{i \theta}\) and using complex integration methods.
- In the 1800’s Weierstrass introduced a method for computing integrals involving rational functions of sine and cosine. One makes the substitution \(t=\tan \frac{\theta}{2}\) and converts the integrand into a rational function of \(t\). Note that the integration around the unit circle corresponds to \(t \in(-\infty, \infty)\).
- Show that \[\sin \theta=\frac{2 t}{1+t^{2}}, \quad \cos \theta=\frac{1-t^{2}}{1+t^{2}} .\nonumber \]
- Show that \[d \theta=\frac{2 d t}{1+t^{2}}\nonumber \]
- Use the Weierstrass substitution to compute the above integral.
Do the following integrals.
- \[\oint_{|z-i|=3} \frac{e^{z}}{z^{2}+\pi^{2}} d z\]
- \[\oint_{|z-i|=3} \frac{z^{2}-3 z+4}{z^{2}-4 z+3} d z .\]
- \[\int_{-\infty}^{\infty} \frac{\sin x}{x^{2}+4} d x\]
[Hint: This is \(\operatorname{Im} \int_{-\infty}^{\infty} \frac{e^{i x}}{x^{2}+4} d x\).]
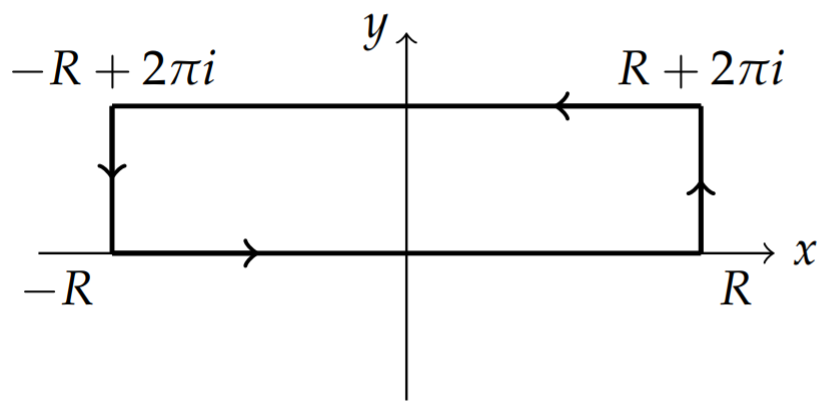
Evaluate the integral \(\int_{0}^{\infty} \frac{(\ln x)^{2}}{1+x^{2}} d x\).
[Hint: Replace \(x\) with \(z=e^{t}\) and use the rectangular contour in Figure \(\PageIndex{1}\) with \(R \rightarrow \infty\).]
Do the following integrals for fun!
- For \(C\) the boundary of the square \(|x| \leq 2,|y| \leq 2\), \[\oint_{C} \frac{d z}{z(z-1)(z-3)^{2}} .\nonumber \]
- \[\int_{0}^{\pi} \frac{\sin ^{2} \theta}{13-12 \cos \theta} d \theta .\nonumber \]
- \[\int_{-\infty}^{\infty} \frac{d x}{x^{2}+5 x+6} .\nonumber \]
- \[\int_{0}^{\infty} \frac{\cos \pi x}{1-9 x^{2}} d x\nonumber \]
- \[\int_{00}^{\infty} \frac{d x}{\left(x^{2}+9\right)(1-x)^{2}}\nonumber \]
- \[\int_{0}^{\infty} \frac{\sqrt{x}}{(1+x)^{2}} d x\nonumber \]
- \[\int_{0}^{\infty} \frac{\sqrt{x}}{(1+x)^{2}} d x\nonumber \]