20.1: Basic trigonometric equations
- Page ID
- 49080
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this section we solve equations such as:
\[\sin(x)=0.5 \nonumber \]
We know that \(x=\dfrac{\pi}{6}\) solves this equation. However, there are also other solutions such as \(x=\dfrac{5\pi}{6}\) or \(x=\dfrac{13\pi}{6}\) that can easily be checked with the calculator. Below, we will study how to find all solutions of equations of the form
\[\sin(x)=c, \quad \cos(x)=c, \quad\text{ and }\quad \tan(x)=c \nonumber \]
We start with equations involving the tangent.
The equation \(\tan(x)=c\)
Solve for \(x\): \(\tan(x)=\sqrt{3}\)
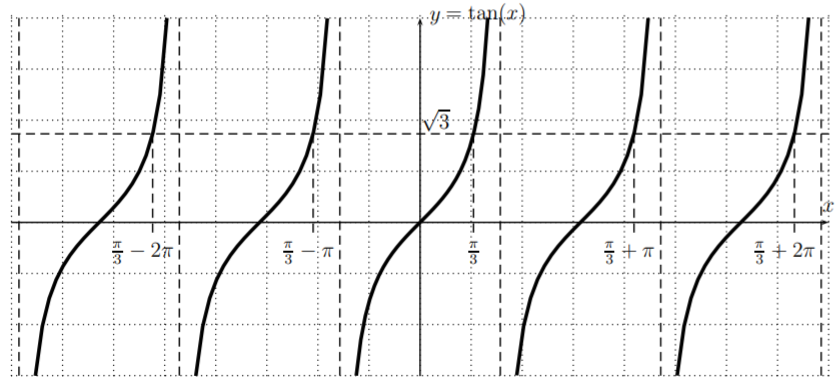
Solution
There is an obvious solution given by \(x=\tan^{-1}(\sqrt{3})=\dfrac{\pi}{3}\), as we studied in the last section. However, we can look for all solutions of \(\tan(x)=\sqrt{3}\) by studying the graph of the tangent function, that is, by finding all points where the graph of the \(y=\tan(x)\) intersects with the horizontal line \(y=\sqrt{3}\). Since the function \(y=\tan(x)\) is periodic with period \(\pi\), we see that the other solutions of \(\tan(x)=\sqrt{3}\) besides \(x=\dfrac{\pi}{3}\) are
\[\dfrac{\pi}{3}+\pi, \quad \dfrac{\pi}{3}+2\pi, \quad \dfrac{\pi}{3}+3\pi, \dots, \quad\text{ and }\quad \dfrac{\pi}{3}-\pi, \quad \dfrac{\pi}{3}-2\pi, \quad \dfrac{\pi}{3}-3\pi, \dots \nonumber \]
In general, we write the solution as
\[x=\dfrac{\pi}{3}+n\cdot \pi, \quad \text{ where } n=0,\pm 1, \pm 2, \pm 3, \dots \nonumber \]
The graph also shows that these are indeed all solutions of \(\tan(x)=\sqrt{3}\).
By the same argument we also get the general solution of \(\tan(x)=c\).
To solve \(\tan(x)=c\), we first determine one solution \(x=\tan^{-1}(c)\). Then the general solution is given by
\[\boxed{x=\tan^{-1}(c)+n\cdot \pi} \quad \text{ where } n=0,\pm 1, \pm 2, \pm 3, \dots \nonumber \]
Solve for \(x\):
- \(\tan(x)=1\)
- \(\tan(x)=-1\)
- \(\tan(x)=5.1\)
- \(\tan(x)=-3.7\)
Solution
- First, we find \(\tan^{-1}(1)=\dfrac{\pi}{4}\). The general solution is thus:
\[x=\dfrac{\pi}{4}+n\cdot \pi \quad \text{ where } n=0,\pm 1, \pm 2, \pm 3, \dots \nonumber \]
- First, we need to find \(\tan^{-1}(-1)\). Recall from equation [EQU:tan-1(-x)] that \(\tan^{-1}(-c)=-\tan^{-1}(c)\), and recall further that \(\tan^{-1}(1)=\dfrac{\pi}{4}\). With this we have
\[\tan^{-1}(-1)=-\tan^{-1}(1)=-\dfrac{\pi}{4} \nonumber \]
The general solution of \(\tan(x)=-1\) is therefore,
\[x=-\dfrac{\pi}{4}+n\cdot \pi,\quad \text{ where } n=0,\pm 1, \pm 2, \dots \nonumber \]
For parts (c) and (d), we do not have an exact solution, so that the solution can only be approximated with the calculator.
- \(x=\tan ^{-1}(5.1)+n \pi \quad \approx 1.377+n \pi, \quad \text { where } n=0, \pm 1, \pm 2, \ldots\)
- \(x=\tan ^{-1}(-3.7)+n \pi \quad \approx-1.307+n \pi, \quad \text { where } n=0, \pm 1, \pm 2, \ldots\)
The equation \(\cos(x)=c\)
We start again with an example.
Solve for \(x\): \(\cos(x)=\dfrac{1}{2}\)
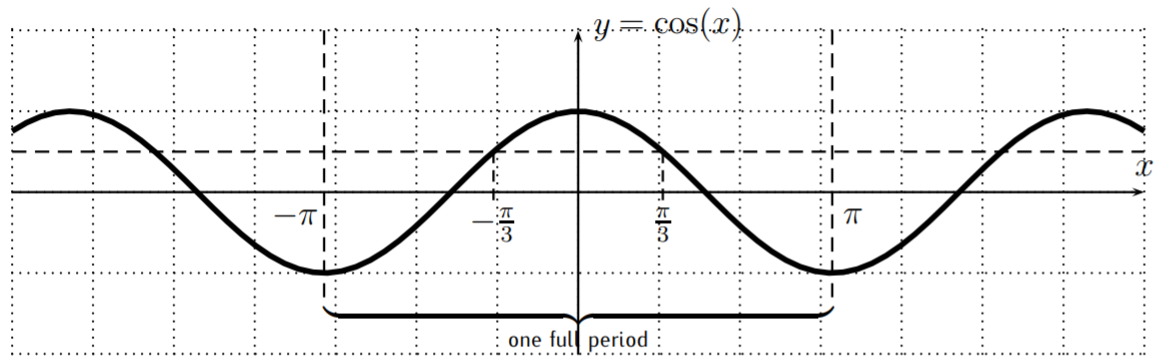
Solution
We have the obvious solution to the equation \(x=\cos^{-1}\left(\dfrac 1 2\right)=\dfrac{\pi}{3}\). However, since \(\cos(-x)=\cos(x)\), there is another solution given by taking \(x=-\dfrac{\pi}{3}\):
\[\cos\Big(-\dfrac{\pi}{3}\Big)=\cos\Big(\dfrac{\pi}{3}\Big)=\dfrac{1}{2} \nonumber \]
Moreover, the \(y=\cos(x)\) function is periodic with period \(2\pi\), that is, we have \(\cos(x+2\pi)=\cos(x)\). Thus, all of the following numbers are solutions of the equation \(\cos(x)=\dfrac 1 2\):
\[\begin{array}{rrrrrrr}
& \ldots, & \dfrac{\pi}{3}-4 \pi, & \dfrac{\pi}{3}-2 \pi, & \dfrac{\pi}{3}, & \dfrac{\pi}{3}+2 \pi, & \dfrac{\pi}{3}+4 \pi, & \ldots, \\
\text { and: } & \ldots, & -\dfrac{\pi}{3}-4 \pi, & -\dfrac{\pi}{3}-2 \pi, & -\dfrac{\pi}{3}, & -\dfrac{\pi}{3}+2 \pi, & -\dfrac{\pi}{3}+4 \pi, & \ldots
\end{array} \nonumber \]
From the graph we see that there are only two solutions of \(\cos(x)=\dfrac 1 2\) within one period. Thus, the above list constitutes all solutions of the equation. With this observation, we may write the general solution as:
\[x=\dfrac{\pi}3+2n\cdot \pi, \text{ or } x=-\dfrac{\pi}{3}+2n\cdot \pi, \quad \text{ where } n=0,\pm 1, \pm 2, \pm 3, \dots\]
In short, we write this as: \(x=\pm\dfrac{\pi}3+2n\cdot \pi\) with \(n=0, \pm 1, \pm 2, \pm 3, \dots\).
We generalize this example as follows.
To solve \(\cos(x)=c\), we first determine one solution \(x=\cos^{-1}(c)\). Then the general solution is given by
\[x=\cos^{-1}(c)+2n\cdot \pi, \text{ or } x=-\cos^{-1}(c)+2n\cdot \pi, \quad \text{ where } n=0,\pm 1, \pm 2, \pm 3, \dots \nonumber \]
In short, we write
\[\boxed{x=\pm\cos^{-1}(c)+2n\cdot \pi } \quad \text{ where } n=0,\pm 1, \pm 2, \pm 3, \dots \nonumber \]
Solve for \(x\).
- \(\cos(x)=-\dfrac{\sqrt{2}}{2}\)
- \(\cos(x)=0.6\)
- \(\cos(x)=-3\)
- \(\cos(x)=-1\)
Solution
- First, we need to find \(\cos^{-1}\left(-\dfrac{\sqrt{2}}{2}\right)\). From equation [EQU:cos-1(-x)] we know that \(\cos^{-1}(-c)=\pi-\cos^{-1}(c)\), so that:
\[\cos^{-1}\bigg(-\dfrac{\sqrt{2}}{2}\bigg)=\quad \pi-\cos^{-1}\bigg(\dfrac{\sqrt{2}}{2}\bigg)= \quad \pi- \dfrac{\pi}{4}=\quad \dfrac{4\pi-\pi}{4}=\quad \dfrac{3\pi}{4}\]
The solution is therefore,
\[x=\pm\dfrac{3\pi}{4}+2n\pi, \quad \text{ where } n=0,\pm 1, \pm 2, \pm 3, \dots \nonumber \]
- We calculate \(\cos^{-1}(0.6)\approx 0.927\) with the calculator. The general solution is therefore,
\[x=\pm\cos^{-1}(0.6)+2n\pi\quad\approx \pm 0.927+2n\pi, \quad \text{ where } n=0,\pm 1, \pm 2, \pm 3, \dots \nonumber\]
- Since the cosine is always \(-1\leq\cos(x)\leq 1\), the cosine can never be \(-3\). Therefore, there is no solution to the equation \(\cos(x)=-3\). This can also be seen from the graph which does not intersect with the horizontal line \(y=-3\).
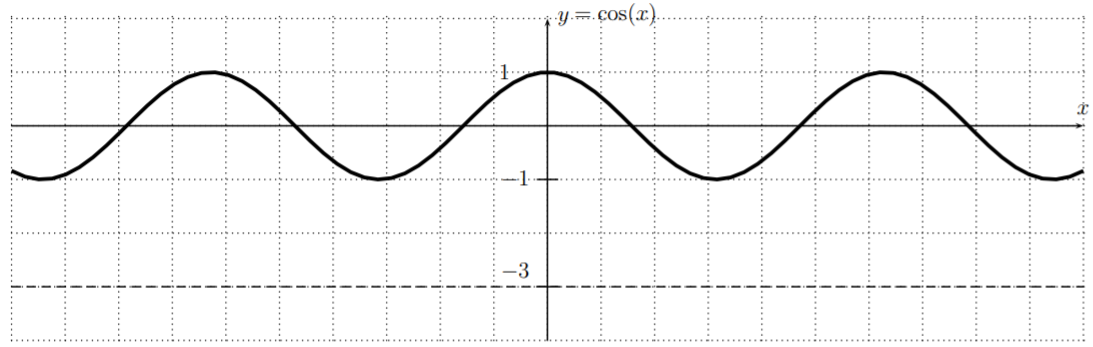
- A special solution of \(\cos(x)=-1\) is
\[\cos^{-1}(-1)=\pi-\cos^{-1}(1)=\pi-0=\pi \nonumber \]
so that the general solution is
\[x=\pm\pi+2n\pi, \quad \text{ where } n=0,\pm 1, \pm 2, \pm 3, \dots \nonumber \]
However, since \(-\pi+2\pi=+\pi\), the solutions \(\pi+2n\pi\) and \(-\pi+2n\pi\) (for \(n=0,\pm1,\pm 2, \dots\)) can be identified with each other, and there is only one solution in each period. Thus, the general solution can be written as
\[x=\pi+2n\pi, \quad \text{ where } n=0,\pm 1, \pm 2, \pm 3, \dots \nonumber \]
The graphs of \(y=\cos(x)\) and \(y=-1\) confirm these considerations.

The equation \(\sin(x)=c\)
Solve for \(x\): \(\sin(x)=\dfrac{\sqrt{2}}{2}\)
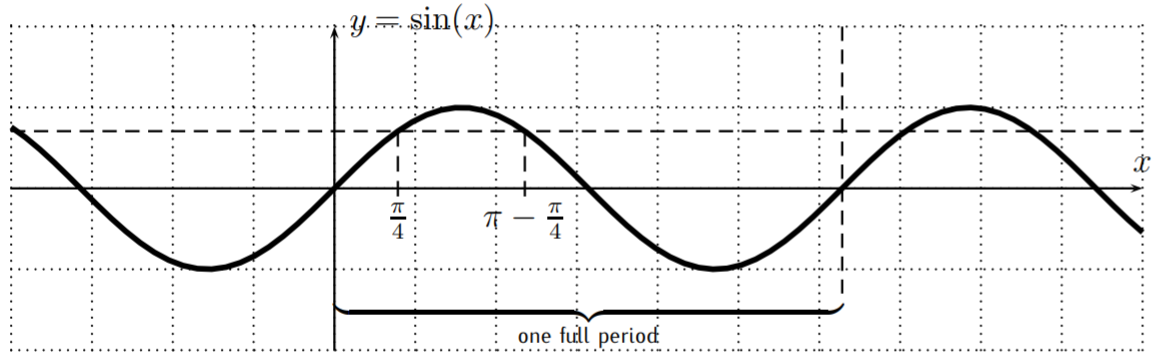
Solution
First, we can find one obvious solution \(x=\sin^{-1}\left(\dfrac{\sqrt{2}}{2}\right)=\dfrac{\pi}{4}\). Furthermore, from the top right equation in [EQU:basic-trig-eqns-wrt-pi], we have that \(\sin(\pi-x)=\sin(x)\), so that another solution is given by \(\pi-\dfrac{\pi}{4}\):
\[\sin\left(\pi-\dfrac{\pi}{4}\right)=\sin\left(\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2} \nonumber \]
(This can also be seen by going back to the unit circle definition.) These are all solutions within one period, as can be checked from the graph above. The function \(y=\sin(x)\) is periodic with period \(2\pi\), so that adding \(2n\cdot \pi\) for any \(n=0,\pm 1, \pm 2, \dots\) gives all solutions of \(\sin(x)=\dfrac{\sqrt{2}}{2}\). This means that the general solution is:
\[x=\dfrac{\pi}{4}+2n\cdot \pi, \text{ or }x=\left(\pi-\dfrac{\pi}{4}\right)+2n\cdot \pi, \quad \text{ for } n=0,\pm 1, \pm 2, \pm 3, \dots \nonumber \]
We rewrite these solutions to obtain one single formula for the solutions. Note, that \(\pi-\dfrac{\pi}{4}+2n\cdot \pi=-\dfrac{\pi}{4}+(2n+1)\cdot \pi\). Therefore, all solutions are of the form
\[x= \pm\dfrac{\pi}{4}+k\cdot \pi \nonumber \]
where, for even \(k=2n\), the sign in front of \(\dfrac{\pi}{4}\) is “\(+\),” and, for odd \(k=2n+1\), the sign in front of \(\dfrac{\pi}{4}\) is “\(-\).” This can be summarized as:
\[x=(-1)^k\cdot \dfrac{\pi}{4}+k\cdot \pi \nonumber \]
Renaming the indexing variable \(k\) to the usual \(n\), we obtain the final version for the solutions of \(\sin(x)=\dfrac{\sqrt{2}}{2}\).
\[x=(-1)^n\cdot\dfrac{\pi}{4}+n\cdot \pi, \quad \text{ where } n=0,\pm 1, \pm 2, \pm 3, \dots \nonumber \]
We have the following general statement.
To solve \(\sin(x)=c\), we first determine one solution \(x=\sin^{-1}(c)\). Then the general solution is given by
\[\boxed{x=(-1)^n\cdot \sin^{-1}(c)+n\cdot \pi} \quad \text{ where } n=0,\pm 1, \pm 2, \pm 3, \dots\]
Solve for \(x\).
- \(\sin(x)=\dfrac{1}{2}\)
- \(\sin(x)=-\dfrac{1}{2}\)
- \(\sin(x)=-\dfrac{5}{7}\)
- \(\sin(x)=1\)
Solution
- First, we calculate \(\sin^{-1}\left(\dfrac 1 2\right)=\dfrac{\pi}{6}\). The general solution is therefore,
\[x=(-1)^n\cdot\dfrac{\pi}{6}+n\cdot \pi, \quad \text{ where } n=0,\pm 1, \pm 2, \pm 3, \dots \nonumber \]
- First, we need to find \(\sin^{-1}\left(-\dfrac 1 2\right)\). From equation [EQU:sin-1(-x)] we know that \(\sin^{-1}(-c)=-\sin^{-1}(c)\), so that \(\sin^{-1}\left(-\dfrac 1 2\right)=-\sin^{-1}\left(\dfrac 1 2\right)=-\dfrac{\pi}{6}\). We thus state the general solution as
\[x=(-1)^{n} \cdot\left(-\dfrac{\pi}{6}\right)+n \cdot \pi=-(-1)^{n} \cdot \dfrac{\pi}{6}+n \cdot \pi=(-1)^{n+1} \cdot \dfrac{\pi}{6}+n \cdot \pi , \text{ where } n=0, \pm 1, \pm 2, \pm 3, \ldots \nonumber \]
- We do not have an exact value of \(\sin^{-1}\left(-\dfrac 5 7\right)\), so that we either need to leave it as this, or approximate this with the calculator \(\sin^{-1}\left(-\dfrac 5 7\right)\approx -0.796\). We get the solution:
\[x \approx(-1)^{n} \cdot(-0.796)+n \cdot \pi=(-1)^{n+1} \cdot 0.796+n \cdot \pi , \text{ where } n=0, \pm 1, \pm 2, \pm 3, \ldots \nonumber \]
- We calculate \(\sin^{-1}(1)=\dfrac{\pi}{2}\). The general solution \(x\) can be written as
\[\label{EQU:a-trig-example} x=(-1)^n\cdot\dfrac{\pi}{2}+n\cdot \pi, \quad \text{ where } n=0,\pm 1, \pm 2, \pm 3, \dots \]
Now, if we look at the graph, we see that each period only has one solution.
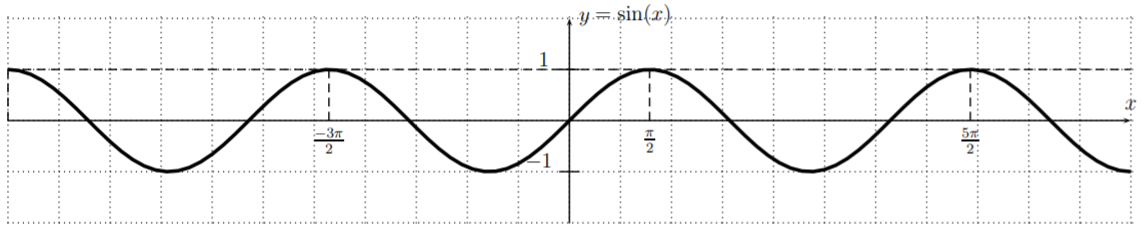
Algebraically, we can see this as follows. For an even number \(n\), the solution \(x=(-1)^n\cdot\dfrac{\pi}{2}+n\cdot \pi\) coincides with the solution coming from the index \(n+1\), that is:
\[\begin{aligned} (-1)^n\cdot\dfrac{\pi}{2}+n\cdot \pi &= +\dfrac{\pi}{2}+n\cdot \pi, \text{ and } \\ (-1)^{n+1}\cdot\dfrac{\pi}{2}+(n+1)\cdot \pi &= -\dfrac{\pi}{2}+(n+1)\cdot \pi = -\dfrac{\pi}{2}+n\cdot \pi +\pi\\ &= +\dfrac{\pi}{2}+n\cdot \pi\end{aligned} \nonumber \]
Therefore, we can write the solution more efficiently by removing the odd solutions (since they coincide with the even solutions), and state this as
\[x=(-1)^n\cdot\dfrac{\pi}{2}+n\cdot \pi, \quad \text{ where } n=0, \pm 2, \pm 4, \dots \nonumber \]
Since \((-1)^n=+1\) for even \(n\), we can just write this as
\[\label{EQU:a-trig-example-simplified} x=\dfrac{\pi}{2}+2n\cdot \pi, \quad \text{ where } n=0, \pm 1, \pm 2, \pm 3, \dots \]
Writing the solutions as \(x=\dfrac{\pi}{2}+2n\cdot \pi\) as in \(\ref{EQU:a-trig-example-simplified}\) instead of the original \(x=(-1)^n\cdot\dfrac{\pi}{2}+n\cdot \pi\) from \(\ref{EQU:a-trig-example}\) for \(n=0,\pm1, \pm2, \dots\) certainly does not change the overall solution set. However, writing the solutions as in \(\ref{EQU:a-trig-example-simplified}\) is more efficient, since it does not repeat any of the solutions, and is therefore a simplified and preferred way of presenting the solutions.
Summary
We summarize the different formulas we used to solve the basic trigonometric equations in the following table.
| Solve: \(\sin (x)=c\) | Solve: \(\cos (x)=c\) | Solve: \(\tan (x)=c\) |
|---|---|---|
|
First, find one solution, that is: \(\sin ^{-1}(c)\) Use: \(\sin ^{-1}(-c)=-\sin ^{-1}(c)\) |
First, find one solution, that is: \(\cos ^{-1}(c)\) Use: \(\cos ^{-1}(-c)= \pi -\cos ^{-1}(c)\) |
First, find one solution, that is: \(\tan ^{-1}(c)\) Use: \(\tan ^{-1}(-c)=-\tan ^{-1}(c)\) |
|
The general solution is: \(\boxed {x=(-1)^{n} \sin ^{-1}(c)+n \pi} \) where \(n=0, \pm 1, \pm 2, \ldots\) |
The general solution is: \(\boxed {x=\pm \cos ^{-1}(c)+2 n \pi} \) where \(n=0, \pm 1, \pm 2, \ldots\) |
The general solution is: \(\boxed {x=\tan ^{-1}(c)+n \pi} \) where \(n=0, \pm 1, \pm 2, \ldots\) |
Find the general solution of the equation, and state at least \(5\) distinct solutions.
- \(\sin(x)=-\dfrac{1}{2}\)
- \(\cos(x)=-\dfrac{\sqrt{3}}{2}\)
Solution
- We already calculated the general solution in example \(\PageIndex{6}\) (b). It is
\[x=(-1)^{n+1}\cdot\dfrac{\pi}{6}+n\cdot \pi, \quad \text{where } n=0,\pm 1, \pm 2, \pm 3, \dots \nonumber \]
We simplify the solutions for \(n=0,1,-1,2,-2\).
\[\begin{aligned} n=0: x&= (-1)^{0+1}\cdot\dfrac{\pi}{6}+0\cdot \pi =-\dfrac{\pi}{6} \\ n=1: x&= (-1)^{1+1}\cdot\dfrac{\pi}{6}+1\cdot \pi =\dfrac{\pi}{6}+\pi =\dfrac{\pi+6\pi}{6}=\dfrac{7\pi}{6} \\ n=-1: x&= (-1)^{-1+1}\cdot\dfrac{\pi}{6}+(-1)\cdot \pi =\dfrac{\pi}{6}-\pi =\dfrac{\pi-6\pi}{6}=\dfrac{-5\pi}{6} \\ n=2: x&= (-1)^{2+1}\cdot\dfrac{\pi}{6}+2\cdot \pi =-\dfrac{\pi}{6}+2\pi =\dfrac{-\pi+12\pi}{6}=\dfrac{11\pi}{6} \\ n=-2: x&= (-1)^{-2+1}\cdot\dfrac{\pi}{6}+(-2)\cdot \pi =-\dfrac{\pi}{6}-2\pi =\dfrac{-\pi-12\pi}{6}=\dfrac{-13\pi}{6}\end{aligned} \nonumber \]
- It is \(\cos^{-1}\left(-\dfrac{\sqrt{3}}{2}\right)=\pi-\cos^{-1}\left(\dfrac{\sqrt{3}}{2}\right)=\pi-\dfrac{\pi}{6}=\dfrac{6\pi-\pi}{6}=\dfrac{5\pi}{6}\). The solutions of \(\cos(x)=-\dfrac{\sqrt{3}}{2}\) are:
\[x=\pm\dfrac{5\pi}{6}+2n\pi, \quad\text{ where } n=0,\pm 1, \pm 2, \pm 3, \dots \nonumber \]
We write the \(6\) solutions with \(n=0,+1,-1\), and for each use the two distinct first terms \(+\dfrac{5\pi}6\) and \(-\dfrac{5\pi}6\).
\[\begin{aligned} n=0: x&= +\dfrac{5\pi}6+2\cdot 0 \cdot \pi=\dfrac{5\pi}6 \\ n=0: x&= -\dfrac{5\pi}6+2\cdot 0 \cdot \pi=-\dfrac{5\pi}6 \\ n=1: x&= +\dfrac{5\pi}6+2\cdot 1 \cdot \pi=\dfrac{5\pi}6+2\pi=\dfrac{5\pi+12\pi}{6}=\dfrac{17\pi}{6} \\ n=1: x&= -\dfrac{5\pi}6+2\cdot 1 \cdot \pi=-\dfrac{5\pi}6+2\pi=\dfrac{-5\pi+12\pi}{6}=\dfrac{7\pi}{6} \\ n=-1: x&= +\dfrac{5\pi}6+2\cdot (-1) \cdot \pi=\dfrac{5\pi}6-2\pi=\dfrac{5\pi-12\pi}{6}=\dfrac{-7\pi}{6} \\ n=-1: x&= -\dfrac{5\pi}6+2\cdot (-1) \cdot \pi=-\dfrac{5\pi}6-2\pi=\dfrac{-5\pi-12\pi}{6}=\dfrac{-17\pi}{6}\end{aligned} \nonumber \]
Further solutions can be found by taking values \(n=+2,-2,+3,-3,\dots\).


