26.5: A.5- Using the table

Last updated
Save as PDF

Page ID: 54492

Thomas Tradler and Holly Carley
CUNY New York City College of Technology via New York City College of Technology at CUNY Academic Works

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

The table ($\boxed{\text{2nd}}$$\boxed{\text{graph}}$) is useful as it gives a table representation of a function (from the $\boxed{y=}$ screen). Make sure there is a function typed in the Y1 postion and look at the table. If you want to know the value of the function for particular values of $x$ then we must use the ’TBLSET’ screen. Press $\boxed{\text{2nd}}$$\boxed{\text{window}}$. Move the cursor to the ’Indpnt’ line then to the right to highlight ask and press $\boxed{\text{enter}}$.

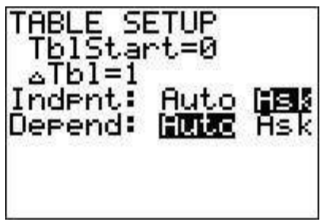
$clipboard_e0ff689b9cb6c0c7839705ec33e4c6784.png$

Go back to the table $\boxed{\text{2nd}}$$\boxed{\text{graph}}$. Now your table is empty. Evaluate your function at $2.5$ by typing $2.5$ and pressing $\boxed{\text{enter}}$. You will see the value of the function in Y1 at $2.5$ in the table now. You can evaluate at any number of points.

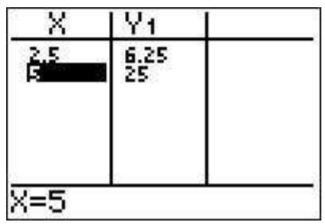
$clipboard_e4d323fddf8768ffa2524ea802af25727.png$

You can also evaluate at every half integer starting at $-1$ for example by going to the ’TBLSET’ screen ($\boxed{\text{2nd}}$$\boxed{\text{window}}$) changing ’TblStart’ to $\boxed{\text{(-)}}$$\boxed{\text{1}}$and $\Delta$Tbl$=.5$. Also change the ‘Indpnt’ setting to ‘Auto’ again.

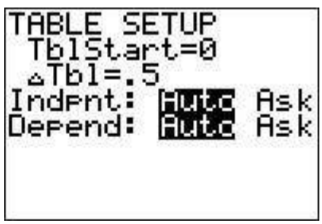
$clipboard_eb96edd9d0079cd9cf9e288d779924540.png$

View the table ($\boxed{\text{2nd}}$$\boxed{\text{graph}}$) to see what happened.