3.4: Finding the Equation of a Line
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Determine the equation of a line given the y intercept and slope
- Use a graph to extract the y intercept and slope of a line to determine its equation
- Determine the equation of a line given the y intercept and a point
- Determine the equation of a line given two points
- Find the y intercept of the graph below
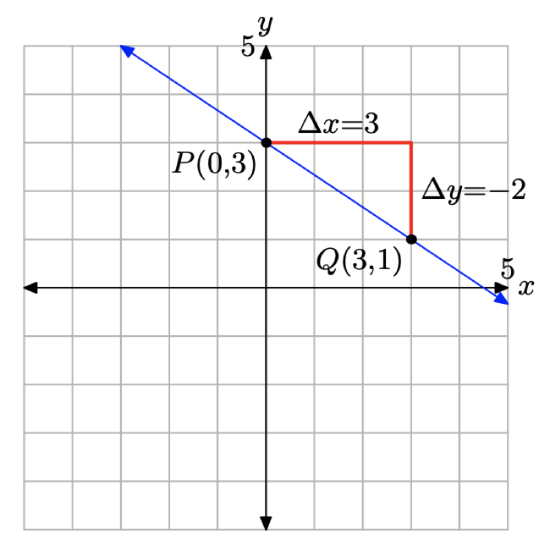
- Find the slope of the line that contains the points (-1, 2) and (3, -6)
- Solve for y to get the equation into slope-intercept form: y−3=−4(x+1).
- Answer
-
- b=−2
- m=−2
- y=−4x−1
In the last few sections, we've talked about how we can use an equation to look at the graphs of a line or points on a line. In this section, we look at different ways to deduce the equation of a line given information such as slope, intercepts, points, or just a graph.
Find an Equation of the Line Given the Slope and y-Intercept
First, let's recall a particularly helpful form for the equation of a line -- the slope-intercept form -- and discuss a strategy we can use to deduce an equation of this form.
If the line L intercepts the y-axis at the point (0, b) and has slope m, then the equation of the line is
y=mx+b.
This form of the equation of a line is called the slope-intercept form. The function defined by the equation f(x)=mx+b
It is important to note two key facts about the slope-intercept form y = mx + b.
- The coefficient of x (the m in y = mx + b) is the slope of the line.
- The constant term (the b in y = mx+b) is the y-coordinate of the y-intercept (0, b).
So in order to create an equation for a line using this form, all we would need to deduce is those two pieces of information, slope and intercept.
When given the slope of a line and the y-intercept of the line, use the slope-intercept form as follows:
- Substitute the given slope for m in the formula y=mx+b.
- Substitute the y-coordinate of the y-intercept for b in the formula y=mx+b.
For example, if the line has slope −2 and the y-intercept (the point where the line crosses the y-axis) is (0, 3), then substitute m = −2 and b = 3 into Equation ??? to obtain
y=−2x+3.
As we did in the last chapter, we can easily determine the slope and intercept of a line if the equation is written in slope-intercept form, y=mx+b. Now we will do the reverse—we will start with the slope and y-intercept and use them to find the equation of the line.
Find the equation of a line with slope −9 and y-intercept (0,−4).
- Answer
-
Since we are given the slope and y-intercept of the line, we can substitute the needed values into the slope-intercept form, y=mx+b.
Name the slope. 
Name the y-intercept. 
Substitute the values into y=mx+b. 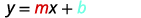
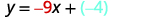
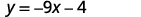
Find the equation of a line with slope 25 and y-intercept (0,4).
- Answer
-
y=25x+4
Find the equation of a line with slope −1 and y-intercept (0,−3).
- Answer
-
y=−x−3
Sometimes, the slope and intercept need to be determined from the graph.
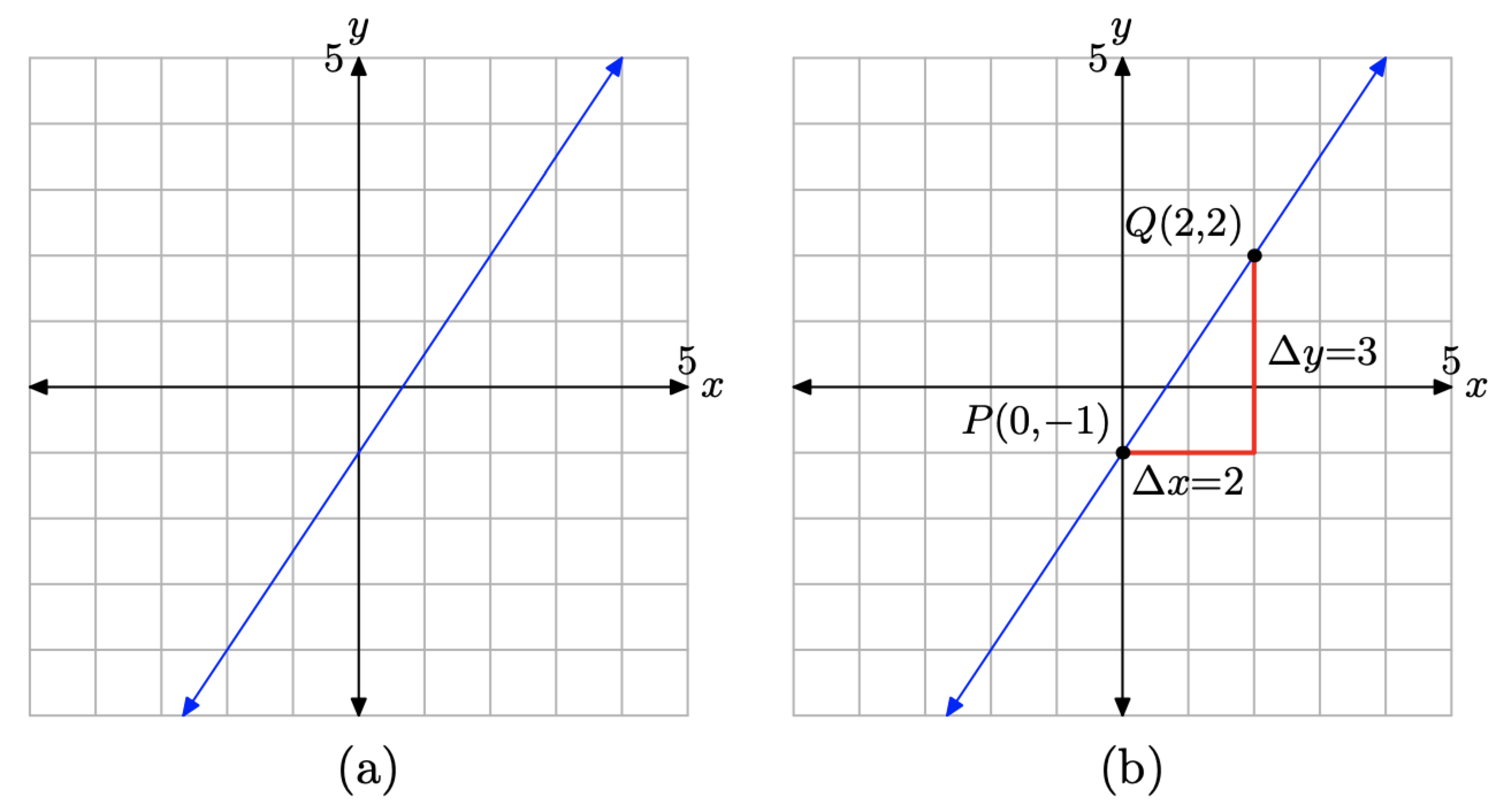
Given the graph of the line in Figure 3.4.4(a), determine the equation of the line.
Solution
First, locate the y-intercept of the line, which we’ve labeled P(0, −1) in Figure 3.4.4(b). In the formula y = mx + b, recall that b represents the y-coordinate of the y-intercept. Thus, b = −1.
Secondly, we need to determine the slope of the line. In Figure 3.4.4(b), start at the point P, move 2 units to the right, then 3 units upward to the point Q(2, 2). This makes the slope m=ΔyΔx=32
Substitute m = 3/2 and b = −1 into the slope-intercept form y = mx + b to obtain
y=32x−1
which is the desired equation of the line.
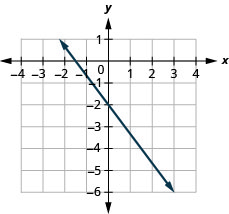
Find the equation of the line shown in the graph.
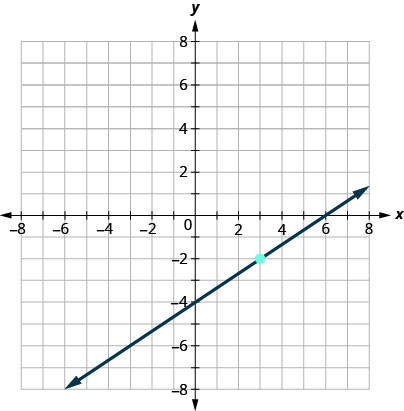
- Answer
-
We need to find the slope and y-intercept of the line from the graph so we can substitute the needed values into the slope-intercept form, y=mx+b.
To find the slope, we choose two points on the graph.
The y-intercept is (0,−4) and the graph passes through (3,−2).
Find the slope, by counting the rise and run. 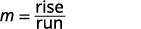

Find the y-intercept. 
Substitute the values into y=mx+b.y=mx+b. 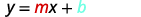
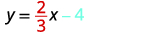
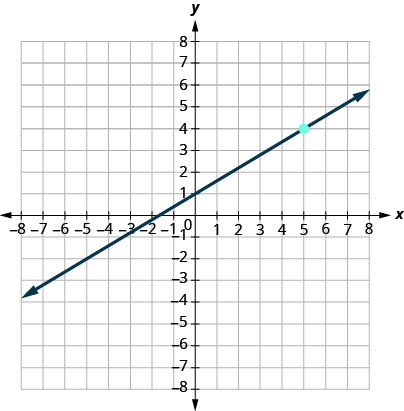
Find the equation of the line shown in the graph.
- Answer
-
y=35x+1
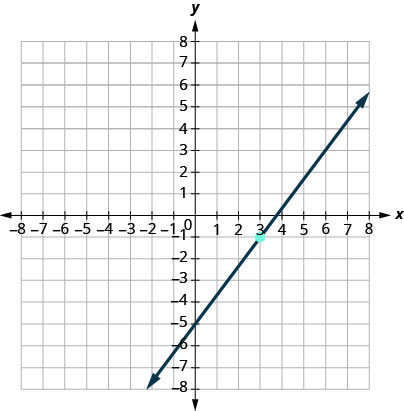
Find the equation of the line shown in the graph.
- Answer
-
y=43x−5
Find an Equation of the Line Given the Slope and a Point
Finding an equation of a line using the slope-intercept form of the equation works well when you are given the slope and y-intercept or when you read them off a graph. But what happens when you have another point instead of the y-intercept?
We are going to use the slope formula to derive another form of an equation of the line.
Suppose we have a line that has slope m and that contains some specific point (x0,y0) and some other point, which we will just call (x,y). We can write the slope of this line and then change it to a different form.
m=y−y0x−x0Multiply both sides of the equation by x−x1.m(x−x1)=(y−y1x−x1)(x−x1)Simplify.m(x−x1)=y−y1Rewrite the equation with theyterms on the left.y−y1=m(x−x1)
This format is called the point-slope form of an equation of a line.
If line L passes through the point (x1,y1) and has slope m, then the equation of the line is y−y1=m(x−x1)
To use the point-slope form of a line, follow these steps.
When given the slope of a line and a point on the line, use the point-slope form as follows:
- Substitute the given slope for m in the formula y−y1=m(x−x1).
- Substitute the coordinates of the given point for x0 and y0 in the formula y−y1=m(x−x1).
For example, if the line has slope −2 and passes through the point (3, 4), then substitute m=−2,x1=3, and y1=4 in the formula y−y1=m(x−x1) to obtain y−4=−2(x−3)
It is common to rewrite this equation in slope-intercept form, because it's such a popular format. To do this, we just get y by itself on the left and then simplify everything on the left:
y−4=−2(x−3)
y=−2(x−3)+4
y=−2x+6+4
y=−2x+10.
We can use the point-slope form of an equation to find an equation of a line when we know the slope and at least one point, even if it's not the y intercept. Then, we will rewrite the equation in slope-intercept form. Most applications of linear equations use the the slope-intercept form.
How to Find an Equation of a Line Given a Point and the Slope
Find an equation of a line with slope m=−13 that contains the point (6,−4). Write the equation in slope-intercept form.
- Answer
-




Find the equation of a line with slope m=−25 and containing the point (10,−5).
- Answer
-
y=−25x−1
Find the equation of a line with slope m=−34, and containing the point (4,−7).
- Answer
-
y=−34x−4
Let's summarize the steps more succinctly for easy reference:
- Identify the slope.
- Identify the point.
- Substitute the values into the point-slope form, y−y1=m(x−x1).
- Write the equation in slope-intercept form.
Find an equation of a horizontal line that contains the point (−2,−6). Write the equation in slope-intercept form.
- Answer
-
Every horizontal line has slope 0. We can substitute the slope and points into the point-slope form, y−y1=m(x−x1).
Identify the slope. 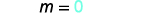
Identify the point. 
Substitute the values into y−y1=m(x−x1).y−y1=m(x−x1). 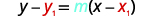
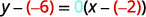
Simplify. 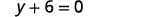
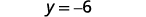
Write in slope-intercept form. It is in y-form, but could be written y=0x−6. Did we end up with the form of a horizontal line, y=a?
Find the equation of a horizontal line containing the point (−3,8).
- Answer
-
y=8
Find the equation of a horizontal line containing the point (−1,4).
- Answer
-
y=4
Find an Equation of the Line Given Two Points
In the next example we’ll see how to find an equation of a line when just two points are given.
So far, we have two options for finding an equation of a line: slope-intercept or point-slope. When we start with two points, it makes more sense to use the point-slope form.
But then we need the slope. Can we find the slope with just two points? Yes. Then, once we have the slope, we can use it and one of the given points to find the equation.
How to Find the Equation of a Line Given Two Points
Find an equation of a line that contains the points (−3,−1) and (2,−2) Write the equation in slope-intercept form.
- Answer
-




Find the equation of a line containing the points (−2,−4) and (1,−3).
- Answer
-
\(y=\frac{1}{3}x−\frac{10{3}\)
Find the equation of a line containing the points (−4,−3) and (1,−5).
- Answer
-
y=−25x−235
The steps are summarized here.
- Find the slope using the given points. m=y2−y1x2−x1
- Choose one point.
- Substitute the values into the point-slope form: y−y1=m(x−x1).
- Write the equation in slope-intercept form.
Find an equation of a line that contains the points (−3,5) and (−3,4). Write the equation in slope-intercept form.
- Answer
-
Again, the first step will be to find the slope.
Find the slope of the line through(−3,5)and(−3,4).
m=y2−y1x2−x1
m=4−5−3−(−3)
m=−10
The slope is undefined.
This tells us it is a vertical line. Both of our points have an x-coordinate of −2. So our equation of the line is x=−2. Since there is no y, we cannot write it in slope-intercept form.
You may want to sketch a graph using the two given points. Does your graph agree with our conclusion that this is a vertical line?
Find the equation of a line containing the points (5,1) and (5,−4).
- Answer
-
x=5
Find the equation of a line containing the points (−4,4) and (−4,3).
- Answer
-
x=−4
We have seen that we can use either the slope-intercept form or the point-slope form to find an equation of a line. Which form we use will depend on the information we are given.
| To Write an Equation of a Line | ||
|---|---|---|
| If given: | Use: | Form: |
| Slope and y-intercept | slope-intercept | y=mx+b |
| A graph | slope-intercept | y=mx+b |
| Slope and a point | point-slope | y−y1=m(x−x1) |
| Two points | point-slope | y−y1=m(x−x1) |
Key Concepts
- There are two useful forms for an equation -- the slope-intercept form and the point-slope form
- The point-slope form is often the easiest to use to create the equation initially
- The slope-intercept form is the most popular final form
- The slope-intercept form of a line is y=mx+b, and only requires the slope m and the y intercept b to create it
- When given the slope of a line and the y-intercept of the line, use the slope-intercept form as follows:
- Substitute the given slope for m in the formula y=mx+b.
- Substitute the y-coordinate of the y-intercept for b in the formula y=mx+b.
- When given the slope of a line and the y-intercept of the line, use the slope-intercept form as follows:
- When we know a point (x1,y1) that is on the line, the point-slope form of a line is y−y1=m(x−x1); but it is commonly rewritten to be in slope-intercept form
- When given the slope of a line and a point on the line that may not be the y intercept, use the point-slope form as follows:
- Identify the slope.
- Identify the point.
- Substitute the values into the point-slope form, y−y1=m(x−x1).
- Write the equation in slope-intercept form.
- When given the slope of a line and a point on the line that may not be the y intercept, use the point-slope form as follows:
- When given two points, (x1,y1) and (x2,y2), the point-slope form is the easiest to use; we just need to do extra work to get the slope first
- Use the point-slope form as follows:
- Find the slope using the given points. m=y2−y1x2−x1
- Choose one point.
- Substitute the values into the point-slope form: y−y1=m(x−x1).
- Write the equation in slope-intercept form.
- Use the point-slope form as follows:

